12.3角的平分线的性质同步练习(无答案)2023-2024学年人教版数学 八年级 上册
文档属性
| 名称 | 12.3角的平分线的性质同步练习(无答案)2023-2024学年人教版数学 八年级 上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 325.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 00:00:00 | ||
图片预览



文档简介
12.3角的平分线的性质
一、选择题。
1.下列条件不能证明两个直角三角形全等的是( )
A.斜边和一直角边对应相等 B.一直角边和一角对应相等
C.两条直角边对应相等 D.斜边和一锐角对应相等
2.如图,在三角形 中, , 平分 交 于点 ,且 , ,则点 到 的距离为( )
A. B. C. D.
3.如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三条角平分线的交点,上述结论中,正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
4.如图,点是的中点,,,平分且,下列结论:;;;.结论中成立的有( )
A.4个 B.3个 C.2个 D.1个
5.如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )
A.DE=DF B.BD=FD C.∠1=∠2 D.AB=AC
6.如图,,若,则的度数为( )
A. B. C. D.
7.如图,在中,,平分交于点D,若,则点D到边的距离的长为( )
A. B. C. D.
8.如图,在中,平分交于点D,于点E,F是BC边上的一点,,若的面积为12,的面积为4,则的面积为( )
A.6 B.6.5 C.7 D.8
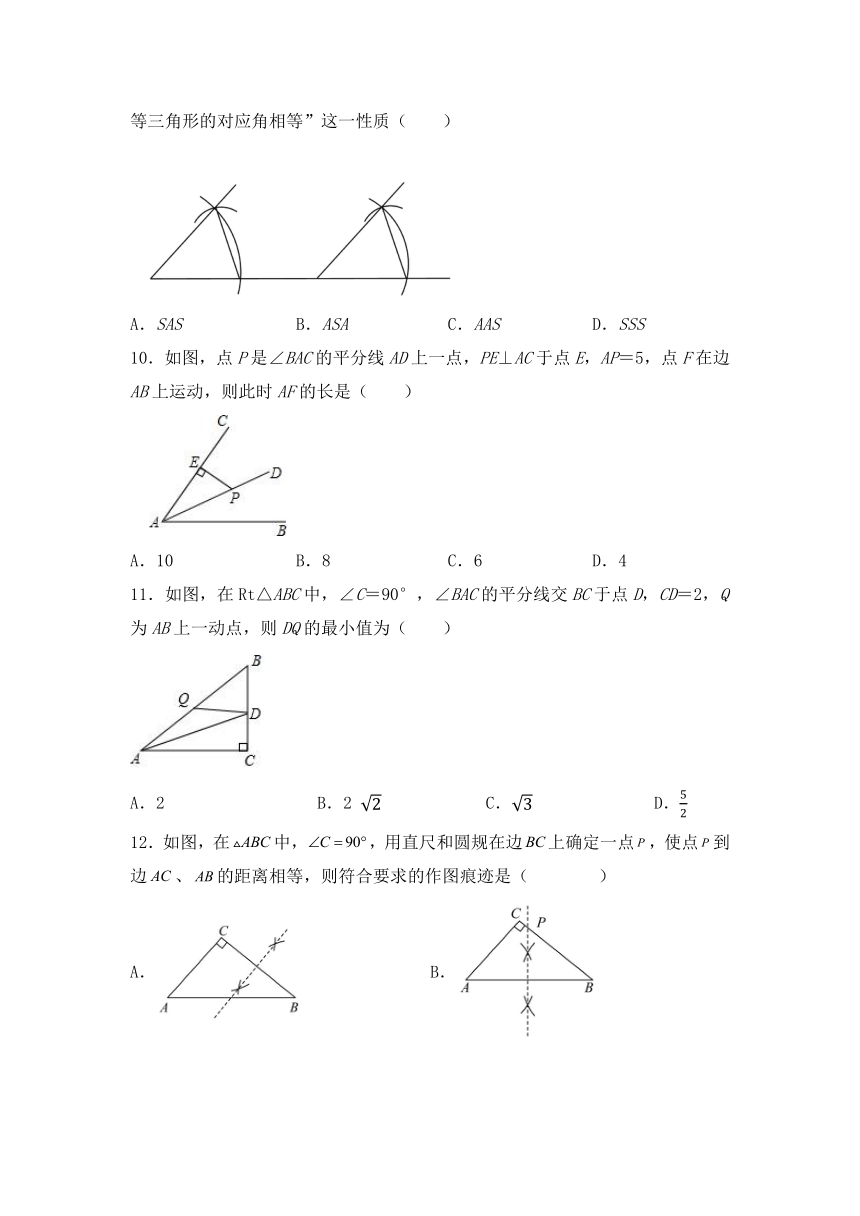
9.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质( )
A.SAS B.ASA C.AAS D.SSS
10.如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,AP=5,点F在边AB上运动,则此时AF的长是( )
A.10 B.8 C.6 D.4
11.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,CD=2,Q为AB上一动点,则DQ的最小值为( )
A.2 B.2 C. D.
12.如图,在中,,用直尺和圆规在边上确定一点,使点到边、的距离相等,则符合要求的作图痕迹是( )
A. B.
C. D.
13.如图,在中,,平分交于点,若,的面积为16,则的长为( )
A.2 B.4 C.6 D.8
14.如图,中,,利用尺规在BC,BA上分别截取BE,BD,使.分别以D,E为圆心、以大于的长为半径作弧,两弧在内交于点F;作射线BF交AC于点G,若,P为AB上一动点,则GP的最小值为( )
A. B.3 C. D.6
二、填空题。
1.△ABC的三边AB、BC、CA的长分别是20、30、40,其三条角平分线相交于O点,将三角形ABC分为三个三角形△ABO:S△BCO:S△CAO= .
2.在△ABC中,∠ABC和∠ACB的平分线交于点D,DE⊥BC于点E,如果DE=1,△ABC的面积是6,则△ABC的周长是 .
3.如图, 中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则 的周长是 cm.
4.如图,为的角平分线,,,则与的面积之比为 .
5.如图,在四边形中,,,,对角线平分,则的面积为 .
6.如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,若DC=6,AB=12,则△ABD的面积是 .
7.如图,在中,是的平分线,,,则 .
三、解答题。
1 如图,已知平分,于E,于F,且.求证:.
2.如图,在Rt△ABC中,∠C=90°,BC=5,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).求BE的长.
3.如图:已知BD=CD,BF⊥AC,CE⊥AB,求证:点D在∠BAC的平分线上.
4.如图,是的平分线,,点在上,、,、分别是垂足,求证:.
5.如图所示,在△ABC中,∠C=90°, AD是 ∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF,证明:CF=EB.
6.如图,△ABC中,三个内角的角平分线交于点O
(1)求∠ABO+∠BCO+∠CAO的度数;
(2)求证:∠BOD=∠COH.
7.如图,已知AE⊥AB,AF⊥AC.AE=AB,AF=AC,BF与CE相交于点M.
(1)EC=BF;
(2)EC⊥BF;
(3)连接AM,求证:AM平分∠EMF.
一、选择题。
1.下列条件不能证明两个直角三角形全等的是( )
A.斜边和一直角边对应相等 B.一直角边和一角对应相等
C.两条直角边对应相等 D.斜边和一锐角对应相等
2.如图,在三角形 中, , 平分 交 于点 ,且 , ,则点 到 的距离为( )
A. B. C. D.
3.如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三条角平分线的交点,上述结论中,正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
4.如图,点是的中点,,,平分且,下列结论:;;;.结论中成立的有( )
A.4个 B.3个 C.2个 D.1个
5.如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )
A.DE=DF B.BD=FD C.∠1=∠2 D.AB=AC
6.如图,,若,则的度数为( )
A. B. C. D.
7.如图,在中,,平分交于点D,若,则点D到边的距离的长为( )
A. B. C. D.
8.如图,在中,平分交于点D,于点E,F是BC边上的一点,,若的面积为12,的面积为4,则的面积为( )
A.6 B.6.5 C.7 D.8
9.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质( )
A.SAS B.ASA C.AAS D.SSS
10.如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,AP=5,点F在边AB上运动,则此时AF的长是( )
A.10 B.8 C.6 D.4
11.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,CD=2,Q为AB上一动点,则DQ的最小值为( )
A.2 B.2 C. D.
12.如图,在中,,用直尺和圆规在边上确定一点,使点到边、的距离相等,则符合要求的作图痕迹是( )
A. B.
C. D.
13.如图,在中,,平分交于点,若,的面积为16,则的长为( )
A.2 B.4 C.6 D.8
14.如图,中,,利用尺规在BC,BA上分别截取BE,BD,使.分别以D,E为圆心、以大于的长为半径作弧,两弧在内交于点F;作射线BF交AC于点G,若,P为AB上一动点,则GP的最小值为( )
A. B.3 C. D.6
二、填空题。
1.△ABC的三边AB、BC、CA的长分别是20、30、40,其三条角平分线相交于O点,将三角形ABC分为三个三角形△ABO:S△BCO:S△CAO= .
2.在△ABC中,∠ABC和∠ACB的平分线交于点D,DE⊥BC于点E,如果DE=1,△ABC的面积是6,则△ABC的周长是 .
3.如图, 中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则 的周长是 cm.
4.如图,为的角平分线,,,则与的面积之比为 .
5.如图,在四边形中,,,,对角线平分,则的面积为 .
6.如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,若DC=6,AB=12,则△ABD的面积是 .
7.如图,在中,是的平分线,,,则 .
三、解答题。
1 如图,已知平分,于E,于F,且.求证:.
2.如图,在Rt△ABC中,∠C=90°,BC=5,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).求BE的长.
3.如图:已知BD=CD,BF⊥AC,CE⊥AB,求证:点D在∠BAC的平分线上.
4.如图,是的平分线,,点在上,、,、分别是垂足,求证:.
5.如图所示,在△ABC中,∠C=90°, AD是 ∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF,证明:CF=EB.
6.如图,△ABC中,三个内角的角平分线交于点O
(1)求∠ABO+∠BCO+∠CAO的度数;
(2)求证:∠BOD=∠COH.
7.如图,已知AE⊥AB,AF⊥AC.AE=AB,AF=AC,BF与CE相交于点M.
(1)EC=BF;
(2)EC⊥BF;
(3)连接AM,求证:AM平分∠EMF.
