12.2 三角形全等的判定 同步练习(无答案) 2023—2024学年人教版八年级数学上册
文档属性
| 名称 | 12.2 三角形全等的判定 同步练习(无答案) 2023—2024学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 544.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 17:04:21 | ||
图片预览

文档简介
12.2 三角形全等的判定 同步精练
一、单选题
1.根据下列已知条件,能够画出唯一的是( )
A.,, B.,,
C.,, D.,,
2.如图,由,,,得的根据是( )
A. B. C. D.
3.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A. B. C. D.
4.如图,为测量池塘两端A、B的距离,小康在池塘外一块平地上选取了一点O,连接,,并分别延长,到点C,D,使得,,连接,测得的长为165米,则池塘两端A,B之间的距离为( )
A.160米 B.165米 C.170米 D.175米
5.如图,已知 ,点 在 上,点 在 上, 和 相交于点 ,且 ,则图中全等三角形共有( )
A. 对 B. 对 C. 对 D. 对
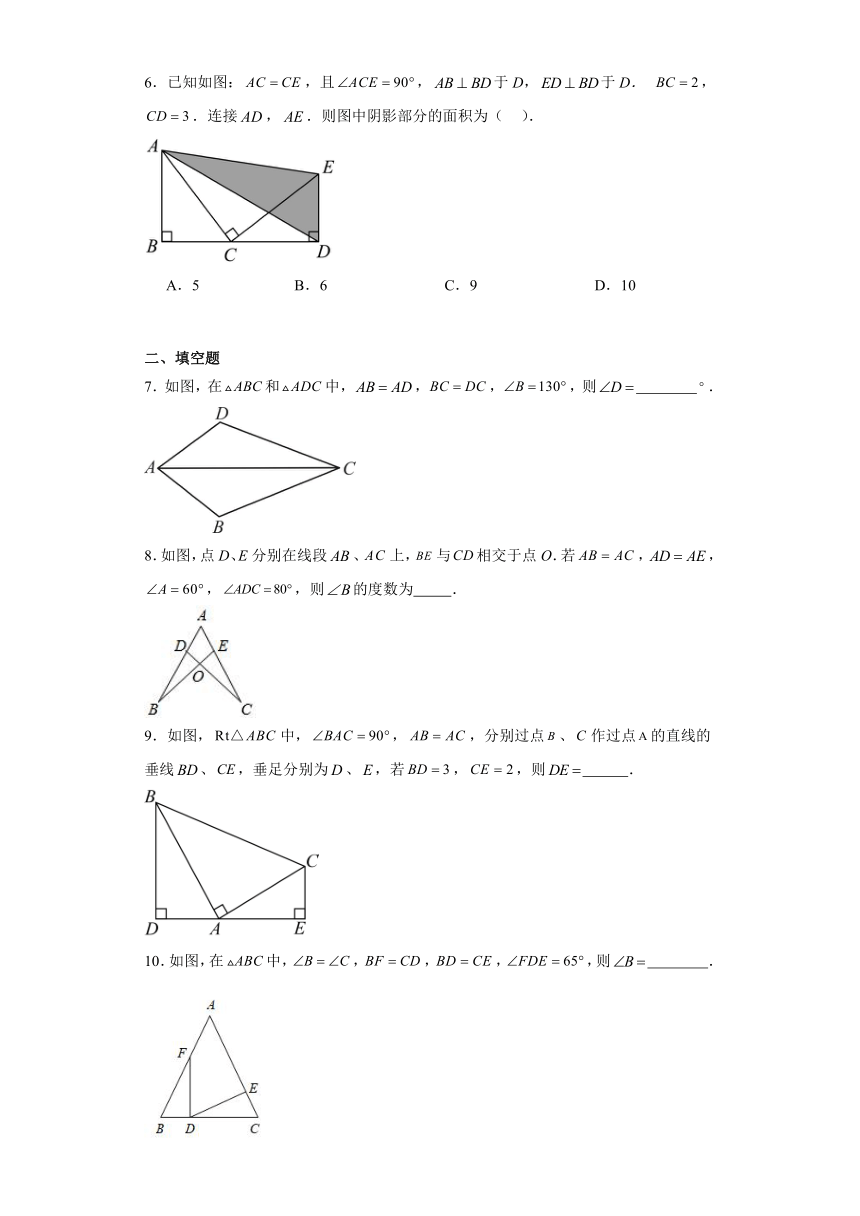
6.已知如图:,且,于D,于D. ,.连接,.则图中阴影部分的面积为( ).
A.5 B.6 C.9 D.10
二、填空题
7.如图,在和中,,,,则 .
8.如图,点D、E分别在线段、上,与相交于点O.若,,,,则的度数为 .
9.如图,中,,,分别过点、作过点的直线的垂线、,垂足分别为、,若,,则 .
10.如图,在中,,,,,则 .
11.如图,已知在中,,,是过点A的直线,,,垂足分别是D、E,若,,则 .
12.如图,cm,cm,,点P在线段上以1cm/s的速度由点A向点B运动.同时,点Q在线段上由点B向点D运动,设运动时间为t(s),则当与全等时,点Q的运动速度为 cm/s.
三、解答题
13.已知:如图,点、、、共线,、相交于点,,,.求证:.
14.如图,,于,于,若,,,,求的长.
15.已知如图,,在上,且,,,求证:与互相平分.
16.如图,的和的平分线,相交于点F,.
(1)求的度数.
(2)求证:.
17.如图,在和中,,,,且点,,在同一直线上,点,在同侧,连接,交于点.
(1)求证:;
(2)若,求的度数.
18.【发现问题】小强在一次学习过程中遇到了下面的问题:如图①,是的中线,若,,求的取值范围.
【探究方法】小强所在的小组通过探究发现,延长至点E,使,连接BE,可以证出,利用全等三角形的性质可将已知的边长与转化到到中,进而求出的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法” .
(1)请你利用上面解答问题的思路方法,写出求的取值范围的过程;
(2)【问题拓展】
如图②,在和中,,,与互补,连接、,E是的中点,求证:.
一、单选题
1.根据下列已知条件,能够画出唯一的是( )
A.,, B.,,
C.,, D.,,
2.如图,由,,,得的根据是( )
A. B. C. D.
3.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A. B. C. D.
4.如图,为测量池塘两端A、B的距离,小康在池塘外一块平地上选取了一点O,连接,,并分别延长,到点C,D,使得,,连接,测得的长为165米,则池塘两端A,B之间的距离为( )
A.160米 B.165米 C.170米 D.175米
5.如图,已知 ,点 在 上,点 在 上, 和 相交于点 ,且 ,则图中全等三角形共有( )
A. 对 B. 对 C. 对 D. 对
6.已知如图:,且,于D,于D. ,.连接,.则图中阴影部分的面积为( ).
A.5 B.6 C.9 D.10
二、填空题
7.如图,在和中,,,,则 .
8.如图,点D、E分别在线段、上,与相交于点O.若,,,,则的度数为 .
9.如图,中,,,分别过点、作过点的直线的垂线、,垂足分别为、,若,,则 .
10.如图,在中,,,,,则 .
11.如图,已知在中,,,是过点A的直线,,,垂足分别是D、E,若,,则 .
12.如图,cm,cm,,点P在线段上以1cm/s的速度由点A向点B运动.同时,点Q在线段上由点B向点D运动,设运动时间为t(s),则当与全等时,点Q的运动速度为 cm/s.
三、解答题
13.已知:如图,点、、、共线,、相交于点,,,.求证:.
14.如图,,于,于,若,,,,求的长.
15.已知如图,,在上,且,,,求证:与互相平分.
16.如图,的和的平分线,相交于点F,.
(1)求的度数.
(2)求证:.
17.如图,在和中,,,,且点,,在同一直线上,点,在同侧,连接,交于点.
(1)求证:;
(2)若,求的度数.
18.【发现问题】小强在一次学习过程中遇到了下面的问题:如图①,是的中线,若,,求的取值范围.
【探究方法】小强所在的小组通过探究发现,延长至点E,使,连接BE,可以证出,利用全等三角形的性质可将已知的边长与转化到到中,进而求出的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法” .
(1)请你利用上面解答问题的思路方法,写出求的取值范围的过程;
(2)【问题拓展】
如图②,在和中,,,与互补,连接、,E是的中点,求证:.
