初中数学人教版八上11.2.1第2课时直角三角形的两个锐角互余 同步课件(共26张PPT)
文档属性
| 名称 | 初中数学人教版八上11.2.1第2课时直角三角形的两个锐角互余 同步课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
第十一章 三角形
11.1 与三角形有关的角
11.2.1 三角形的内角
第2课时 直角三角形的两个锐角互余
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.了解直角三角形两个锐角的关系.(重点)
2.掌握直角三角形的判定.(重点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
新课导入
1.三角形的内角和是多少度
复习引入
180°
3.直角三角形中,有一个角一定是 °.
90
2.按角的大小分类,三角形可以分为哪三类?
锐角三角形、直角三角形和钝角三角形
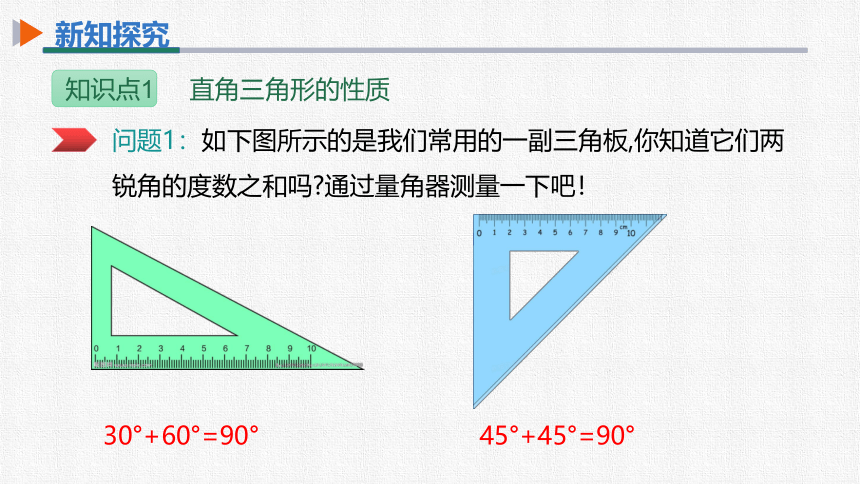
问题1:如下图所示的是我们常用的一副三角板,你知道它们两
锐角的度数之和吗 通过量角器测量一下吧!
30°+60°=90°
45°+45°=90°
新知探究
知识点1 直角三角形的性质
新课导入
问题2:如图,在△ABC中, 已知∠C=90°,(1)你能求出∠A ,∠B的度数吗?
知识点1 直角三角形的性质
能.
在△ABC中,因为 ∠C=90°,所以由三角形内角和
定理,得∠A +∠B+∠C=90°,即∠A +∠B=90°.
不能.
(2)你能求出∠A +∠B的度数吗?你是怎么得到的?
新知探究
知识点1 直角三角形的性质
思考:由此,你可以得到直角三角形有什么性质呢?
直角三角形的性质:直角三角形的两个锐角互余.
几何语言:
在△ABC 中,∵∠C =90°,
∴∠A +∠B =90°.
新知探究
图
知识点1 直角三角形的性质
直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC .
注意:Rt△后必须紧跟表示直角三角形的三个
顶点的大写字母,不能单独使用.
直角三角形的表示:
新知探究
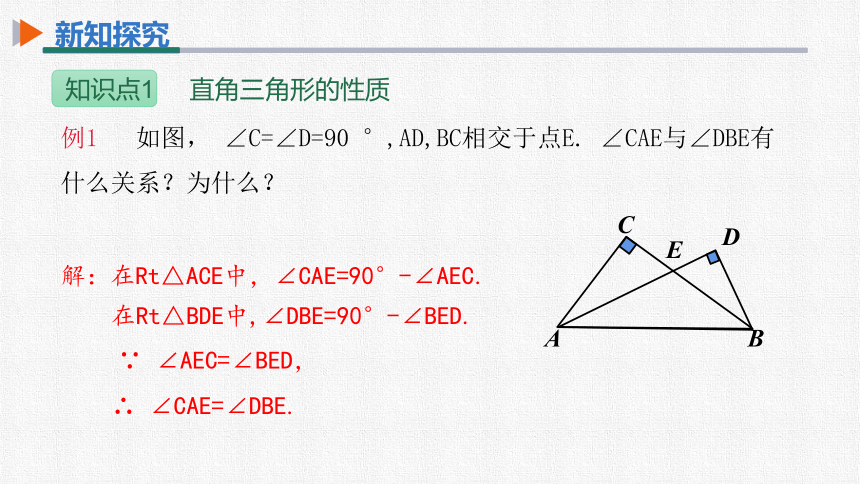
例1 如图, ∠C=∠D=90 °,AD,BC相交于点E. ∠CAE与∠DBE有什么关系?为什么?
A
B
C
D
E
解:在Rt△ACE中,∠CAE=90°-∠AEC.
在Rt△BDE中,∠DBE=90°-∠BED.
∵ ∠AEC=∠BED,
∴ ∠CAE=∠DBE.
知识点1 直角三角形的性质
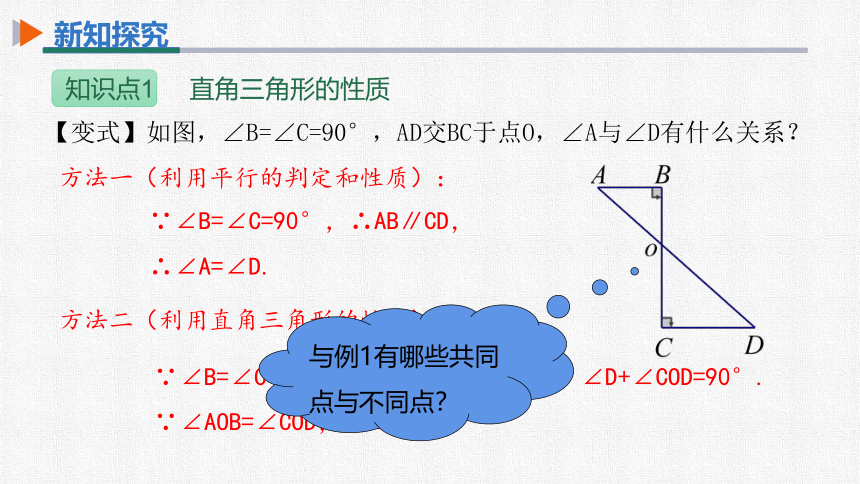
【变式】如图,∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?
新知探究
知识点1 直角三角形的性质
方法一(利用平行的判定和性质):
∵∠B=∠C=90°,∴AB∥CD,∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,∴∠A=∠D.
与例1有哪些共同点与不同点?
新知探究
∠A=∠C
∠A=∠D
基本图形
两个直角三角形的一对锐角为对顶角,则另一对锐角相等.
新知探究
1.(2021苏州模拟)在一个直角三角形中,有一个锐角等于40°,则另一个锐角的度数是( )
A.40° B.50° C.60° D.70°
跟踪训练
B
2.在△ABC中,∠A=90°,∠B=2∠C,则∠C的度数为( )
A.30° B.45° C.60° D.30°或60°
A
新知探究
3.如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,已知∠1=32°,求∠D的度数.
跟踪训练
注意:在直角三角形中,若已知一个锐角
或者两个锐角之间的关系,可以直接运用
两个锐角互余求解,不需要再利用三角形
的内角和定理求解.
解:∵∠BAC=90°,∠1=32°,
∴∠ABC=90°-32°=58°.
∵BD平分∠ABC,
∴∠ABD= ∠ABC=29°.
∵CD∥AB,
∴∠D=∠ABD=29°.
知识点2 直角三角形的判定
新知探究
问题:有两个角互余的三角形是直角三角形吗?如何验证?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC是直角三角形吗?
在△ABC中,由三角形内角和可知 ∠A +∠B +∠C=180°,
又∠A +∠B=90°,所以∠C=90°.
于是△ABC是直角三角形.
新知探究
知识点2 直角三角形的判定
几何语言:
思考:由此,你可以得到直角三角形的判定方法吗?
直角三角形的判定:有两个角互余的三角形是直角三角形.
在△ABC 中,
∵∠A +∠B =90°,
∴△ABC 是直角三角形.
新知探究
知识点2 直角三角形的判定
三角形是直角三角形
三角形的两个角互余
直角三角形的性质与判定之间的关系:
新知探究
例2 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,求证:CD⊥AB.
证明:∵∠ACB=90°,∴∠A+∠B=90°.
∵∠ACD=∠B,∴∠A+∠ACD=90°.
∴∠ADC=90°,∴CD⊥AB.
知识点2 直角三角形的判定
【变式】(2021北京平谷区一模)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
A.∠1+∠2=90° B.∠2=∠3
C.∠1=∠4 D.∠1=30°
D
【解析】∵∠ACB=90°,∴∠1+∠2=90°,故A选项正确;
∵CD⊥AB,∴∠ADC=90°,∴∠1+∠3=90°,∵∠1+∠2=90°,
∴∠2=∠3,故B选项正确;∵CD⊥AB,∴∠BDC=90°,∴∠2+∠4=90°,∵∠1+∠2=90°,∴∠1=∠4,故C选项正确;
根据已知条件不能推出∠1=30°,故D选项符合题意;故选D.
新知探究
知识点2 直角三角形的判定
新知探究
∠1=∠2,∠C=90°,ED⊥AB
已知其中任意两条,即可求得第三条
∠1=∠2,∠3=∠4,∠ACB=90°,CD⊥AB
已知其中任意三条,即可求得第四条
基本图形
课堂小结
直角三角形的性质与判定
性质
判定
直角三角形的两个锐角互余
有两个角互余的三角形是直角三角形
课堂训练
1.如图,在△ABC中,∠ACB=90°,且CD∥AB.∠B=60°,则∠1等于( )
A.30° B.40° C.50° D.60°
A
课堂训练
2.如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
A.40° B.50° C.60° D.70°
A
课堂训练
D
3.下列说法中错误的是( )
A.在△ABC中,若∠A:∠B:∠C=2:2:4,则△ABC为直角三角形
B.在△ABC中,若∠A=∠B-∠C,则△ABC为直角三角形
C.在△ABC中,若∠A= ∠B= ∠C,则△ABC为直角三角形
D.在△ABC中,∠A=∠B=2∠C,则△ABC为直角三角形
【解析】列方程求解.A.解得∠C=90°∠A=∠B=45°,∴△ABC为直角三角形.B.可解得∠B=90°,∴△ABC为直角三角形.C.解得∠C=90°,∠B=60°,∠A=30°,∴△ABC为直角三角形.D.解得∠A=∠B=72°,∠C=36°,∴△ABC不是直角三角形.故选D.
课堂训练
4.如图,将一张长方形纸片剪去一部分后得到一个三角形,则图中∠1+∠2=________.
90°
直角
5.在△ABC中,若∠A=51°,∠B=39°,则这个三角形是____________
三角形.
6.在直角三角形中,锐角α是另一个内角的一半,则锐角α的度数为 .
45°或30°
【解析】①当锐角α是直角的一半时,α= ×90°=45°;
②当锐角α是另一锐角的一半时,α= (90°-α),解得α=30°.
综上所述,锐角α的度数为45°或30°.
课堂训练
7.如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是直角三角形吗?为什么?
理由如下:
课堂训练
解:△ABD是直角三角形.
∵CE⊥AD,∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,∴∠A+∠D=90°,
∴△ABD是直角三角形.
8.如图,∠AOB=50°,点P是边OB上一个动点(不与点O重合),当∠A的度数为多少时,△AOP为直角三角形.
解:若△AOP为直角三角形,则
课堂训练
①∠A=90°时,△AOP为直角三角形;
②当∠APO=90°时,△AOP为直角三角形,此时∠A=40°.
故∠A的度数为90°或40°时,△AOP为直角三角形.
第十一章 三角形
11.1 与三角形有关的角
11.2.1 三角形的内角
第2课时 直角三角形的两个锐角互余
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.了解直角三角形两个锐角的关系.(重点)
2.掌握直角三角形的判定.(重点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
新课导入
1.三角形的内角和是多少度
复习引入
180°
3.直角三角形中,有一个角一定是 °.
90
2.按角的大小分类,三角形可以分为哪三类?
锐角三角形、直角三角形和钝角三角形
问题1:如下图所示的是我们常用的一副三角板,你知道它们两
锐角的度数之和吗 通过量角器测量一下吧!
30°+60°=90°
45°+45°=90°
新知探究
知识点1 直角三角形的性质
新课导入
问题2:如图,在△ABC中, 已知∠C=90°,(1)你能求出∠A ,∠B的度数吗?
知识点1 直角三角形的性质
能.
在△ABC中,因为 ∠C=90°,所以由三角形内角和
定理,得∠A +∠B+∠C=90°,即∠A +∠B=90°.
不能.
(2)你能求出∠A +∠B的度数吗?你是怎么得到的?
新知探究
知识点1 直角三角形的性质
思考:由此,你可以得到直角三角形有什么性质呢?
直角三角形的性质:直角三角形的两个锐角互余.
几何语言:
在△ABC 中,∵∠C =90°,
∴∠A +∠B =90°.
新知探究
图
知识点1 直角三角形的性质
直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC .
注意:Rt△后必须紧跟表示直角三角形的三个
顶点的大写字母,不能单独使用.
直角三角形的表示:
新知探究
例1 如图, ∠C=∠D=90 °,AD,BC相交于点E. ∠CAE与∠DBE有什么关系?为什么?
A
B
C
D
E
解:在Rt△ACE中,∠CAE=90°-∠AEC.
在Rt△BDE中,∠DBE=90°-∠BED.
∵ ∠AEC=∠BED,
∴ ∠CAE=∠DBE.
知识点1 直角三角形的性质
【变式】如图,∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?
新知探究
知识点1 直角三角形的性质
方法一(利用平行的判定和性质):
∵∠B=∠C=90°,∴AB∥CD,∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,∴∠A=∠D.
与例1有哪些共同点与不同点?
新知探究
∠A=∠C
∠A=∠D
基本图形
两个直角三角形的一对锐角为对顶角,则另一对锐角相等.
新知探究
1.(2021苏州模拟)在一个直角三角形中,有一个锐角等于40°,则另一个锐角的度数是( )
A.40° B.50° C.60° D.70°
跟踪训练
B
2.在△ABC中,∠A=90°,∠B=2∠C,则∠C的度数为( )
A.30° B.45° C.60° D.30°或60°
A
新知探究
3.如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,已知∠1=32°,求∠D的度数.
跟踪训练
注意:在直角三角形中,若已知一个锐角
或者两个锐角之间的关系,可以直接运用
两个锐角互余求解,不需要再利用三角形
的内角和定理求解.
解:∵∠BAC=90°,∠1=32°,
∴∠ABC=90°-32°=58°.
∵BD平分∠ABC,
∴∠ABD= ∠ABC=29°.
∵CD∥AB,
∴∠D=∠ABD=29°.
知识点2 直角三角形的判定
新知探究
问题:有两个角互余的三角形是直角三角形吗?如何验证?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC是直角三角形吗?
在△ABC中,由三角形内角和可知 ∠A +∠B +∠C=180°,
又∠A +∠B=90°,所以∠C=90°.
于是△ABC是直角三角形.
新知探究
知识点2 直角三角形的判定
几何语言:
思考:由此,你可以得到直角三角形的判定方法吗?
直角三角形的判定:有两个角互余的三角形是直角三角形.
在△ABC 中,
∵∠A +∠B =90°,
∴△ABC 是直角三角形.
新知探究
知识点2 直角三角形的判定
三角形是直角三角形
三角形的两个角互余
直角三角形的性质与判定之间的关系:
新知探究
例2 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,求证:CD⊥AB.
证明:∵∠ACB=90°,∴∠A+∠B=90°.
∵∠ACD=∠B,∴∠A+∠ACD=90°.
∴∠ADC=90°,∴CD⊥AB.
知识点2 直角三角形的判定
【变式】(2021北京平谷区一模)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
A.∠1+∠2=90° B.∠2=∠3
C.∠1=∠4 D.∠1=30°
D
【解析】∵∠ACB=90°,∴∠1+∠2=90°,故A选项正确;
∵CD⊥AB,∴∠ADC=90°,∴∠1+∠3=90°,∵∠1+∠2=90°,
∴∠2=∠3,故B选项正确;∵CD⊥AB,∴∠BDC=90°,∴∠2+∠4=90°,∵∠1+∠2=90°,∴∠1=∠4,故C选项正确;
根据已知条件不能推出∠1=30°,故D选项符合题意;故选D.
新知探究
知识点2 直角三角形的判定
新知探究
∠1=∠2,∠C=90°,ED⊥AB
已知其中任意两条,即可求得第三条
∠1=∠2,∠3=∠4,∠ACB=90°,CD⊥AB
已知其中任意三条,即可求得第四条
基本图形
课堂小结
直角三角形的性质与判定
性质
判定
直角三角形的两个锐角互余
有两个角互余的三角形是直角三角形
课堂训练
1.如图,在△ABC中,∠ACB=90°,且CD∥AB.∠B=60°,则∠1等于( )
A.30° B.40° C.50° D.60°
A
课堂训练
2.如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
A.40° B.50° C.60° D.70°
A
课堂训练
D
3.下列说法中错误的是( )
A.在△ABC中,若∠A:∠B:∠C=2:2:4,则△ABC为直角三角形
B.在△ABC中,若∠A=∠B-∠C,则△ABC为直角三角形
C.在△ABC中,若∠A= ∠B= ∠C,则△ABC为直角三角形
D.在△ABC中,∠A=∠B=2∠C,则△ABC为直角三角形
【解析】列方程求解.A.解得∠C=90°∠A=∠B=45°,∴△ABC为直角三角形.B.可解得∠B=90°,∴△ABC为直角三角形.C.解得∠C=90°,∠B=60°,∠A=30°,∴△ABC为直角三角形.D.解得∠A=∠B=72°,∠C=36°,∴△ABC不是直角三角形.故选D.
课堂训练
4.如图,将一张长方形纸片剪去一部分后得到一个三角形,则图中∠1+∠2=________.
90°
直角
5.在△ABC中,若∠A=51°,∠B=39°,则这个三角形是____________
三角形.
6.在直角三角形中,锐角α是另一个内角的一半,则锐角α的度数为 .
45°或30°
【解析】①当锐角α是直角的一半时,α= ×90°=45°;
②当锐角α是另一锐角的一半时,α= (90°-α),解得α=30°.
综上所述,锐角α的度数为45°或30°.
课堂训练
7.如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是直角三角形吗?为什么?
理由如下:
课堂训练
解:△ABD是直角三角形.
∵CE⊥AD,∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,∴∠A+∠D=90°,
∴△ABD是直角三角形.
8.如图,∠AOB=50°,点P是边OB上一个动点(不与点O重合),当∠A的度数为多少时,△AOP为直角三角形.
解:若△AOP为直角三角形,则
课堂训练
①∠A=90°时,△AOP为直角三角形;
②当∠APO=90°时,△AOP为直角三角形,此时∠A=40°.
故∠A的度数为90°或40°时,△AOP为直角三角形.
