22.3实际问题与二次函数提高训练(含答案)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 22.3实际问题与二次函数提高训练(含答案)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 399.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 00:00:00 | ||
图片预览



文档简介
22.3实际问题与二次函数
一、单选题
1.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h =﹣5t2+20t﹣14,则小球距离地面的最大高度是( )
A.2米 B.5米 C.6米 D.14米
2.小明乘坐摩天轮转一圈,他离地面的高度(米)与旋转时间(分)之间的关系可以近似地用二次函数来刻画. 经测试得出部分数据如下表:下列选项中,最接近摩天轮转一圈的时间的是( )
/分 … 2. 66 3. 23 3. 46 …
/米 … 69. 16 69. 62 68. 46 …
A.8分 B.7分 C.6分 D.5分
3.某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y=x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )
A.252元/间 B.256元/间 C.258元/间 D.260元/间
4.如图,在矩形ABCD中,AB=a,BC=b,≤a≤3b,AE=AH=CF=CG,则四边形EFGH的面积的最大值是( )
A. B. C. D.
5.李叔叔为了充分利用现有资源,计划用一块矩形空地种植两种蔬菜,如图,矩形的一面靠墙(墙的长度为).另外三面用栅栏围成,中间再用栅栏把它分成两个矩形,已知栅栏的总长度为,若,矩形的面积为,则关于的函数表达式及的取值范围正确的是( )
A. B.
C. D.
6.抛物线与直线交于,两点,抛物线在,两点之间的部分以及线段所围域内(包括边界)恰有4个整点(横、纵坐标都是整数的点叫做整点),则的取值范围是( )
A. B. C. D.
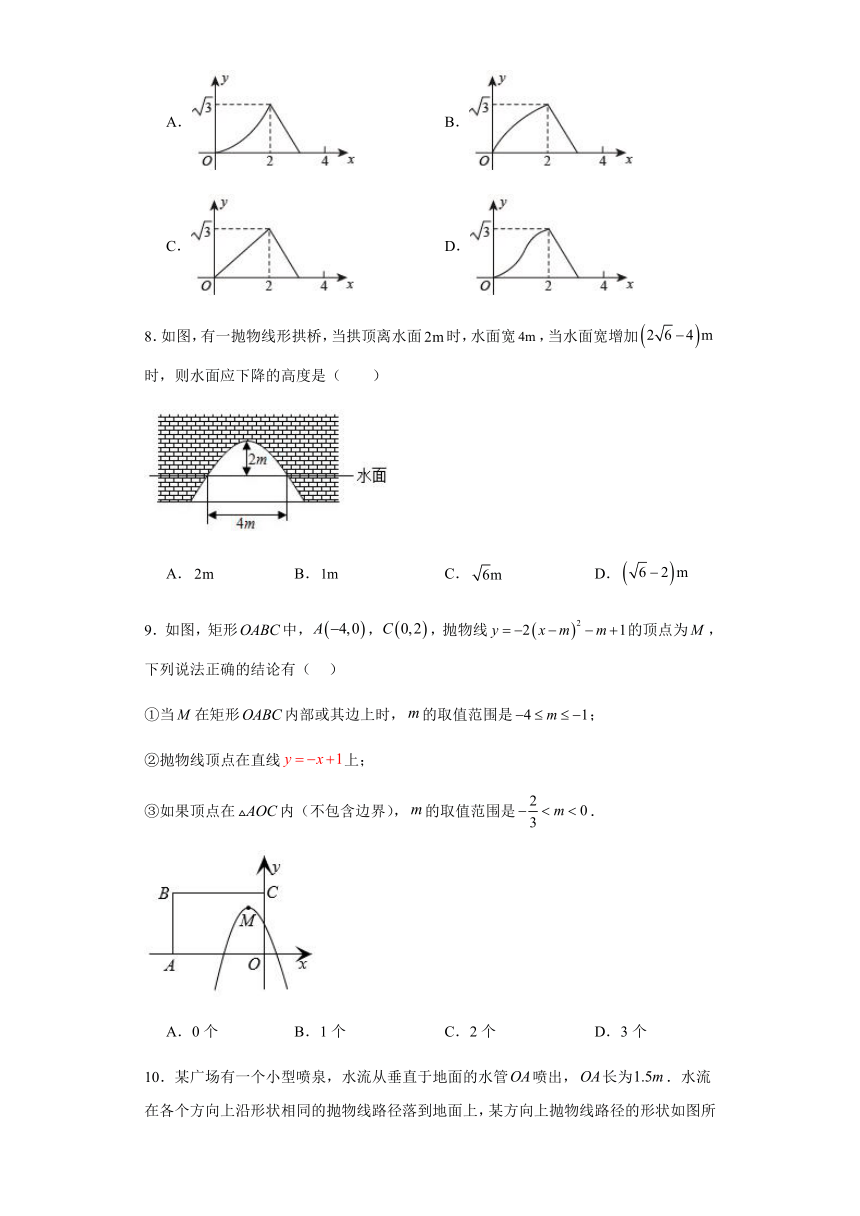
7.如图,点P,Q从边长为2的等边三角形的点B出发,分别沿着,两边以相同的速度在的边上运动,当两点在边上运动到重合时停止.在此过程中,设点P,Q移动过程中各自的路程为x,所得的面积为y,则y随x变化的函数图象大致为( )
A. B.
C. D.
8.如图,有一抛物线形拱桥,当拱顶离水面时,水面宽,当水面宽增加时,则水面应下降的高度是( )
A. B. C. D.
9.如图,矩形中,,,抛物线的顶点为,下列说法正确的结论有( )
①当在矩形内部或其边上时,的取值范围是;
②抛物线顶点在直线上;
③如果顶点在内(不包含边界),的取值范围是.
A.0个 B.1个 C.2个 D.3个
10.某广场有一个小型喷泉,水流从垂直于地面的水管喷出,长为.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点到的距离为.建立平面直角坐标系,水流喷出的高度与水平距离之间近似满足函数关系,则水流喷出的最大高度为( )
A. B. C. D.
二、填空题
11.某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是 .
12.一个小球在空中飞行时,飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系式为,则小球从飞出到落地要用的时间为 s.
13.某网店某种商品成本为50元/件,售价为60元/件时,每天可销售100件;售价单价高于60元时,每涨价1元,日销售量就减少2件.据此,当销售单价为 元时,网店该商品每天盈利最多.
14.如图是一座抛物线形拱桥,当水面的宽为12m时,拱顶离水面4m,当水面下降2m时,水面的宽为 m.
15.如图(1),在中,,,边上的点从顶点出发,向顶点运动,同时,边上的点从顶点出发,向顶点运动,,两点运动速度的大小相等,设,,关于的函数图象如图(2),图象过点,则图象最低点的横坐标是 .
16.丰都县某中学为培养学生综合实践能力,开展了一系列综合实践活动,有一次财商训练活动中,小明同学准备去集市批发两种商品用于活动中交易.预先了解到A、B两种商品的价格之和为27元,小明计划购买B商品的数量比A商品的数量多2件,但一共不超过25件,且每样不少于3件,但小明去购买时发现A商品正打九折销售,而B商品的价格提高了20%,小明决定将A、B产品的购买数量对调,这样实际花费只比计划多8元,已知价格和购买数量均为整数,则小明购买两种商品实际花费为 元.
三、解答题
17.图中是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?
18.某批发商以40元/千克的价格购入了某种水果700千克.据市场预测,该种水果的售价y(元/千克)与保存时间x(天)的函数关系为y=50+2x.但保存这批水果平均每天将耗损15千克,且最多能保存8天.另外.批发商保存该批水果每天还需50元的费用.
(1)填空:若开发商保存3天后将该批水果一次性卖出,则卖出时水果的售价为 (元/千克)
(2)设批发商将这批水果保存x天后一次性卖出.求批发商所获得的总利润w(元)与保存时间x(天)之间的函数关系式;
(3)填空:在(2)的条件下,批发商经营这批水果所获得的最大利润为 .
19.某农户家的菜地上有一个蔬菜大棚,其横截面顶部为抛物线型,现对其横截面建立如图所示的平面直角坐标系.大棚的一端固定在墙体离地面高米的点处,另一端固定在地面的点处,已知大棚上横截面抛物线顶部某点离地面的垂直高度(米)与其离墙体的水平距离(米)之间的关系满足,现测得点到墙体之间的水平距离为10米.
(1)求抛物线的表达式;
(2)求大棚的最高点到地面的距离;
(3)该农户想在大棚横截面抛物线项部两侧,紧贴抛物线顶部安装照明灯,且照明灯到地面垂真高度为米,则两个照明灯的水平距离是多少米?
20.如图1,一灌溉车正为绿化带浇水,喷水口离地竖直高度为米.建立如图2所示的平面直角坐标系,可以把灌溉车喷出水的上、下边缘抽象为两条抛物线的部分图象,把绿化带横截面抽象为矩形,其水平宽度米,竖直高度米,下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点离喷水口的水平距离为2米,高出喷水口米,灌溉车到绿化带的距离为米.
(1)求上边缘抛物线喷出水的最大射程;
(2)求下边缘抛物线与轴交点的坐标;
(3)若米,灌溉车行驶时喷出的水______(填“能”或“不能”)浇灌到整个绿化带.
参考答案:
1.C
2.C
3.B
4.B
5.B
6.A
7.A
8.B
9.C
10.D
11.
12.2
13.80
14.
15.
16.312.
17.
18.(1)56
(2)w=-30x2+600x+7000;
(3)9880元.
(1)(2)大棚的最高点到地面的距离为3米
(3)两个照明灯的水平距离是米
20.(1)上边缘抛物线喷出水的最大射程为;(2);(3)不能.
一、单选题
1.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h =﹣5t2+20t﹣14,则小球距离地面的最大高度是( )
A.2米 B.5米 C.6米 D.14米
2.小明乘坐摩天轮转一圈,他离地面的高度(米)与旋转时间(分)之间的关系可以近似地用二次函数来刻画. 经测试得出部分数据如下表:下列选项中,最接近摩天轮转一圈的时间的是( )
/分 … 2. 66 3. 23 3. 46 …
/米 … 69. 16 69. 62 68. 46 …
A.8分 B.7分 C.6分 D.5分
3.某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y=x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )
A.252元/间 B.256元/间 C.258元/间 D.260元/间
4.如图,在矩形ABCD中,AB=a,BC=b,≤a≤3b,AE=AH=CF=CG,则四边形EFGH的面积的最大值是( )
A. B. C. D.
5.李叔叔为了充分利用现有资源,计划用一块矩形空地种植两种蔬菜,如图,矩形的一面靠墙(墙的长度为).另外三面用栅栏围成,中间再用栅栏把它分成两个矩形,已知栅栏的总长度为,若,矩形的面积为,则关于的函数表达式及的取值范围正确的是( )
A. B.
C. D.
6.抛物线与直线交于,两点,抛物线在,两点之间的部分以及线段所围域内(包括边界)恰有4个整点(横、纵坐标都是整数的点叫做整点),则的取值范围是( )
A. B. C. D.
7.如图,点P,Q从边长为2的等边三角形的点B出发,分别沿着,两边以相同的速度在的边上运动,当两点在边上运动到重合时停止.在此过程中,设点P,Q移动过程中各自的路程为x,所得的面积为y,则y随x变化的函数图象大致为( )
A. B.
C. D.
8.如图,有一抛物线形拱桥,当拱顶离水面时,水面宽,当水面宽增加时,则水面应下降的高度是( )
A. B. C. D.
9.如图,矩形中,,,抛物线的顶点为,下列说法正确的结论有( )
①当在矩形内部或其边上时,的取值范围是;
②抛物线顶点在直线上;
③如果顶点在内(不包含边界),的取值范围是.
A.0个 B.1个 C.2个 D.3个
10.某广场有一个小型喷泉,水流从垂直于地面的水管喷出,长为.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点到的距离为.建立平面直角坐标系,水流喷出的高度与水平距离之间近似满足函数关系,则水流喷出的最大高度为( )
A. B. C. D.
二、填空题
11.某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是 .
12.一个小球在空中飞行时,飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系式为,则小球从飞出到落地要用的时间为 s.
13.某网店某种商品成本为50元/件,售价为60元/件时,每天可销售100件;售价单价高于60元时,每涨价1元,日销售量就减少2件.据此,当销售单价为 元时,网店该商品每天盈利最多.
14.如图是一座抛物线形拱桥,当水面的宽为12m时,拱顶离水面4m,当水面下降2m时,水面的宽为 m.
15.如图(1),在中,,,边上的点从顶点出发,向顶点运动,同时,边上的点从顶点出发,向顶点运动,,两点运动速度的大小相等,设,,关于的函数图象如图(2),图象过点,则图象最低点的横坐标是 .
16.丰都县某中学为培养学生综合实践能力,开展了一系列综合实践活动,有一次财商训练活动中,小明同学准备去集市批发两种商品用于活动中交易.预先了解到A、B两种商品的价格之和为27元,小明计划购买B商品的数量比A商品的数量多2件,但一共不超过25件,且每样不少于3件,但小明去购买时发现A商品正打九折销售,而B商品的价格提高了20%,小明决定将A、B产品的购买数量对调,这样实际花费只比计划多8元,已知价格和购买数量均为整数,则小明购买两种商品实际花费为 元.
三、解答题
17.图中是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?
18.某批发商以40元/千克的价格购入了某种水果700千克.据市场预测,该种水果的售价y(元/千克)与保存时间x(天)的函数关系为y=50+2x.但保存这批水果平均每天将耗损15千克,且最多能保存8天.另外.批发商保存该批水果每天还需50元的费用.
(1)填空:若开发商保存3天后将该批水果一次性卖出,则卖出时水果的售价为 (元/千克)
(2)设批发商将这批水果保存x天后一次性卖出.求批发商所获得的总利润w(元)与保存时间x(天)之间的函数关系式;
(3)填空:在(2)的条件下,批发商经营这批水果所获得的最大利润为 .
19.某农户家的菜地上有一个蔬菜大棚,其横截面顶部为抛物线型,现对其横截面建立如图所示的平面直角坐标系.大棚的一端固定在墙体离地面高米的点处,另一端固定在地面的点处,已知大棚上横截面抛物线顶部某点离地面的垂直高度(米)与其离墙体的水平距离(米)之间的关系满足,现测得点到墙体之间的水平距离为10米.
(1)求抛物线的表达式;
(2)求大棚的最高点到地面的距离;
(3)该农户想在大棚横截面抛物线项部两侧,紧贴抛物线顶部安装照明灯,且照明灯到地面垂真高度为米,则两个照明灯的水平距离是多少米?
20.如图1,一灌溉车正为绿化带浇水,喷水口离地竖直高度为米.建立如图2所示的平面直角坐标系,可以把灌溉车喷出水的上、下边缘抽象为两条抛物线的部分图象,把绿化带横截面抽象为矩形,其水平宽度米,竖直高度米,下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点离喷水口的水平距离为2米,高出喷水口米,灌溉车到绿化带的距离为米.
(1)求上边缘抛物线喷出水的最大射程;
(2)求下边缘抛物线与轴交点的坐标;
(3)若米,灌溉车行驶时喷出的水______(填“能”或“不能”)浇灌到整个绿化带.
参考答案:
1.C
2.C
3.B
4.B
5.B
6.A
7.A
8.B
9.C
10.D
11.
12.2
13.80
14.
15.
16.312.
17.
18.(1)56
(2)w=-30x2+600x+7000;
(3)9880元.
(1)(2)大棚的最高点到地面的距离为3米
(3)两个照明灯的水平距离是米
20.(1)上边缘抛物线喷出水的最大射程为;(2);(3)不能.
同课章节目录
