23.1图形的旋转提高训练(含答案)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 23.1图形的旋转提高训练(含答案)2023-2024学年人教版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 451.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 00:00:00 | ||
图片预览


文档简介
23.1图形的旋转
一、单选题
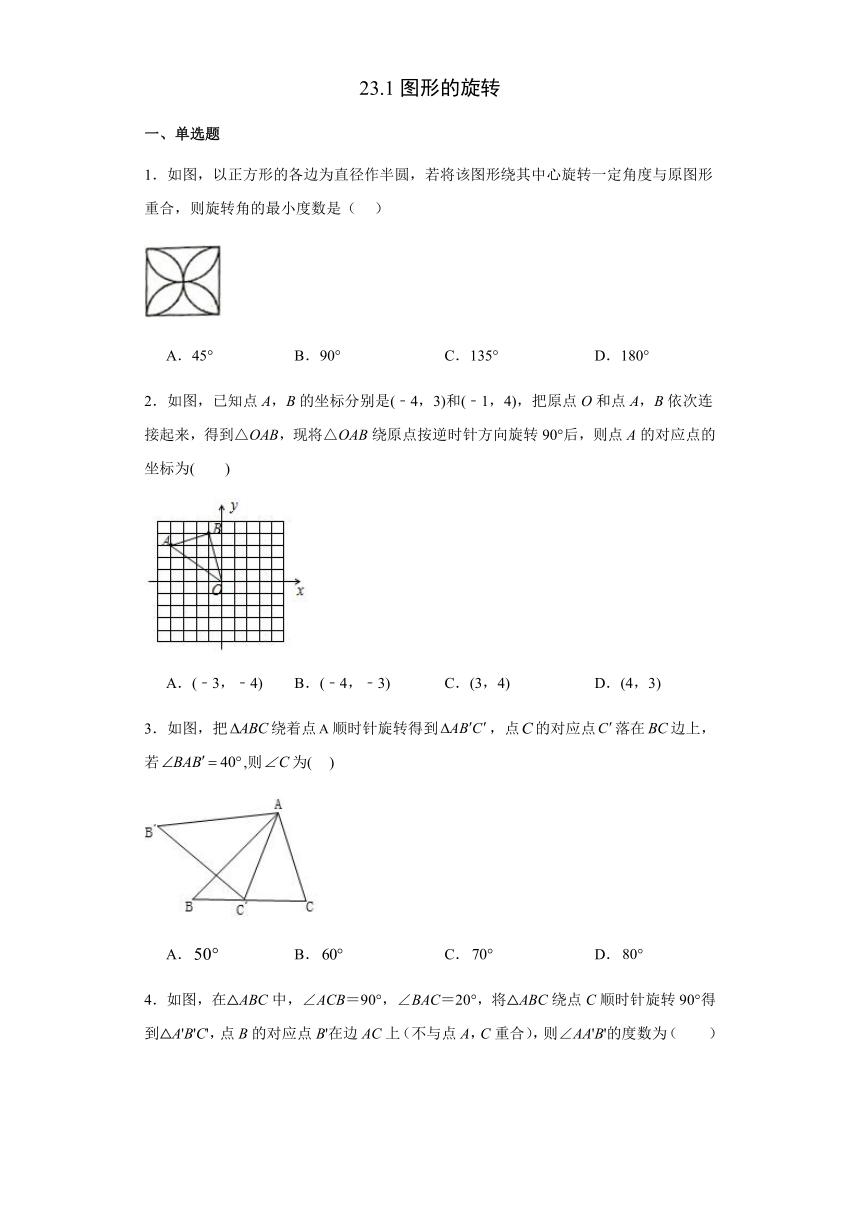
1.如图,以正方形的各边为直径作半圆,若将该图形绕其中心旋转一定角度与原图形重合,则旋转角的最小度数是( )
A.45° B.90° C.135° D.180°
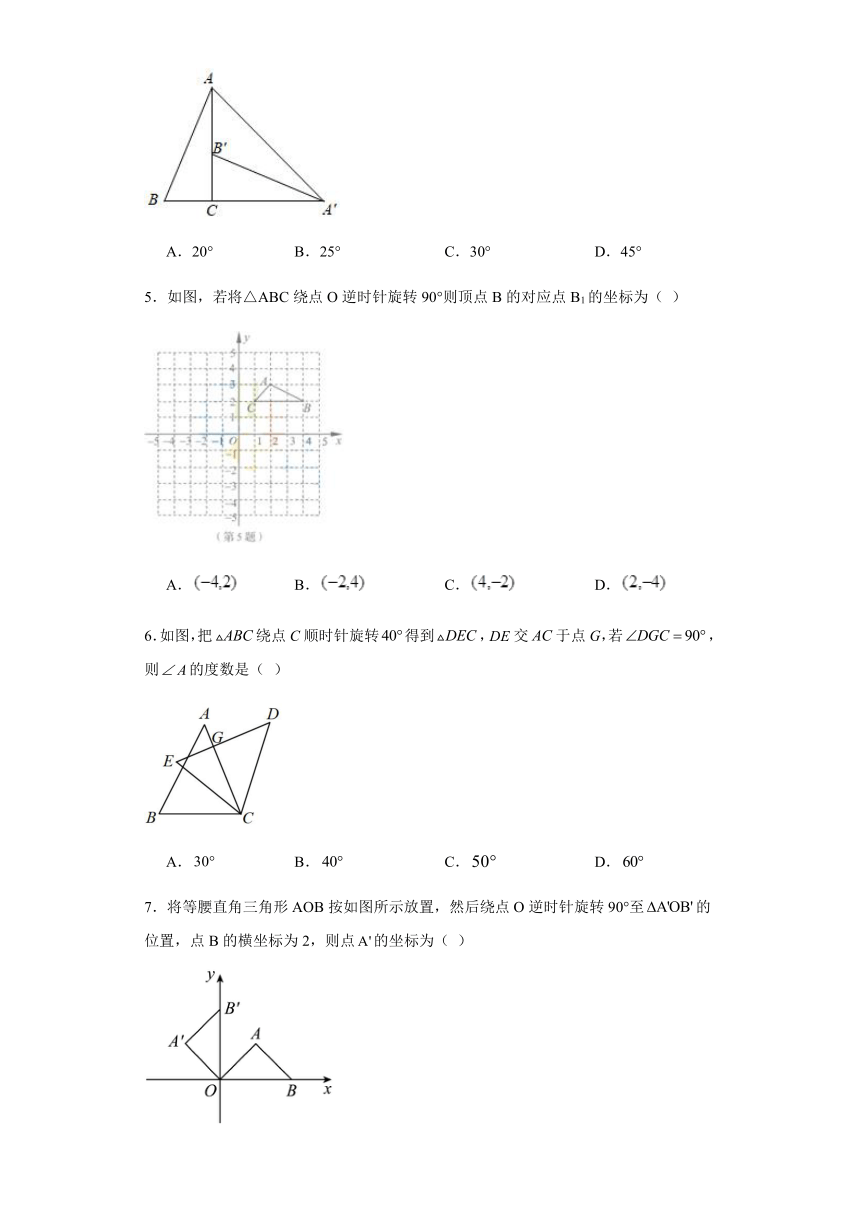
2.如图,已知点A,B的坐标分别是(﹣4,3)和(﹣1,4),把原点O和点A,B依次连接起来,得到△OAB,现将△OAB绕原点按逆时针方向旋转90°后,则点A的对应点的坐标为( )
A.(﹣3,﹣4) B.(﹣4,﹣3) C.(3,4) D.(4,3)
3.如图,把绕着点顺时针旋转得到,点的对应点落在边上,若,则为( )
A. B. C. D.
4.如图,在△ABC中,∠ACB=90°,∠BAC=20°,将△ABC绕点C顺时针旋转90°得到△A'B'C',点B的对应点B'在边AC上(不与点A,C重合),则∠AA'B'的度数为( )
A.20° B.25° C.30° D.45°
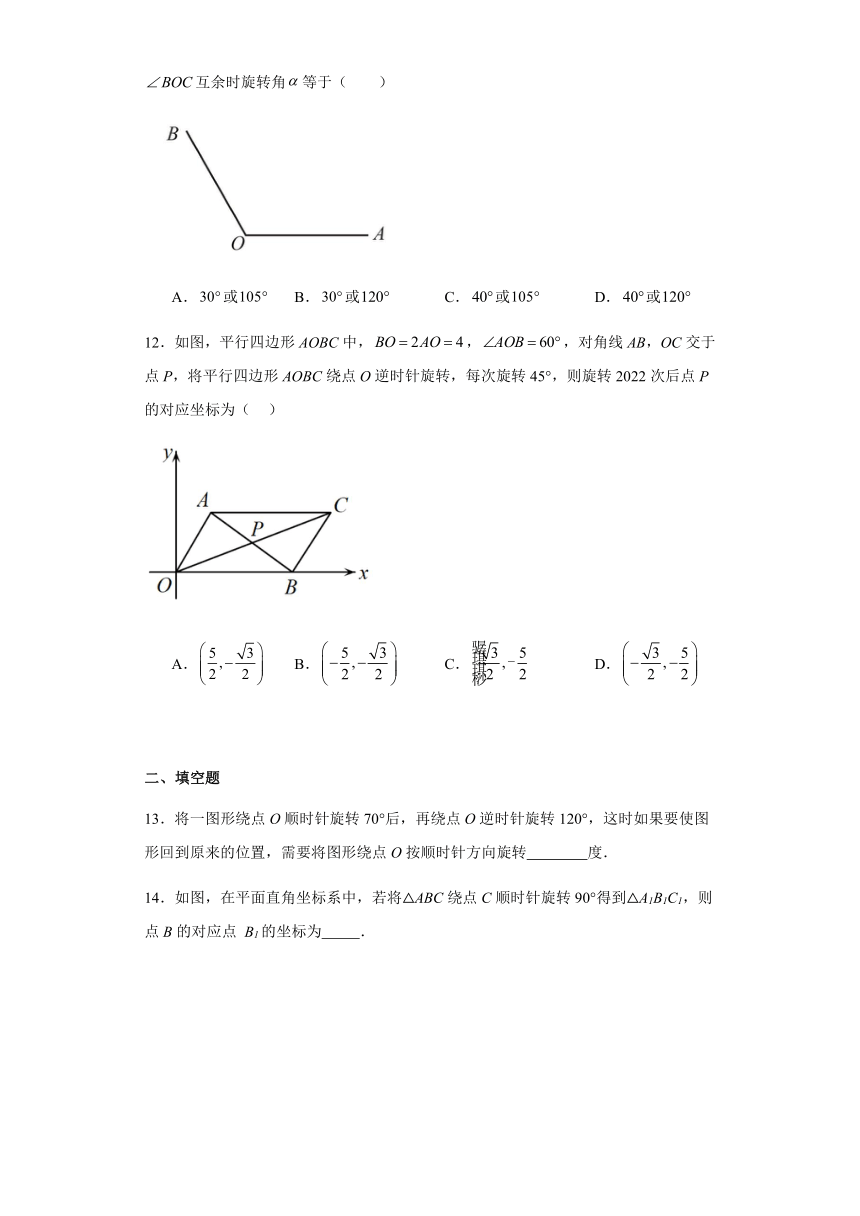
5.如图,若将△ABC绕点O逆时针旋转90°则顶点B的对应点B1的坐标为( )
A. B. C. D.
6.如图,把绕点C顺时针旋转得到,交于点G,若,则的度数是( )
A. B. C. D.
7.将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至的位置,点B的横坐标为2,则点的坐标为( )
A.(1,1) B.() C.(-1,1) D.()
8.如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连结
CD.若AB=4cm. 则△BCD的面积为( )
A.4 B.2 C.3 D.2
9.如图,中,,将沿轴依次以三角形三个顶点为旋转中心顺时针旋转,分别得图②,图③,则旋转到图⑩时直角顶点的坐标是( )
A. B. C. D.
10.如图,P是等边三角形内一点,且,,,以下3个结论:①;②;③;④若点P到三边的距离分别为,,,则有,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
11.如图,,射线在平面内.射线绕点从射线的反向延长线的位置出发,顺时针旋转角,已知平分,当与互余时旋转角等于( )
A.或 B.或 C.或 D.或
12.如图,平行四边形AOBC中,,,对角线AB,OC交于点P,将平行四边形AOBC绕点O逆时针旋转,每次旋转45°,则旋转2022次后点P的对应坐标为( )
A. B. C. D.
二、填空题
13.将一图形绕点O顺时针旋转70°后,再绕点O逆时针旋转120°,这时如果要使图形回到原来的位置,需要将图形绕点O按顺时针方向旋转 度.
14.如图,在平面直角坐标系中,若将△ABC绕点C顺时针旋转90°得到△A1B1C1,则点B的对应点 B1的坐标为 .
15.如图,在中,,,将绕点顺时针旋转得到,点的对应点恰好落在边上,连接,则的度数为 .
16.如图,正△ABC的边长为4,将正△ABC绕点B顺时针旋转120°得到△C'A'B,若点D为直线A'B上的一动点,则AD+CD的最小值是 .
17.如图,已知点P是等边内一点,,,.将线段AP绕点A逆时针旋转60°得到AQ,连接PQ,CQ.则的面积为 .
18.如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,则∠A′的度数为 .
19.若一次函数y=kx+8(k≠0)的图象与x轴、y轴分别交于A、B两点,当k的取值变化时,点A随之在x轴上运动,将线段AB绕点B逆时针旋转90°得到BQ,连接OQ,则OQ长的最小值是 .
三、解答题
20.如图,下列的图案是由什么基本图案经怎样的旋转得到的,把它画出来?
21.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,1),B(4,2),C(3,5).
(1)求△ABC的面积;
(2)在图中画出△ABC绕点A逆时针旋转90°得到的△A'B'C',并写出点C的对应点C'的坐标.
22.如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0).
(1)画出将ABC向上平移1个单位长度,再向右平移5个单位长度后得到的,点A、B、C的对应点分别为、、;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到的,点A、B的对应点分别为、.
23.如图,将一副直角三角尺(其中,)的直角顶点C叠放在一起.保持三角尺BCE不动,三角尺ACD的CD边与CB边重合,然后将三角尺ACD绕点C按逆时针方向转动,形成.
(1)如图①,当时,吗?为什么?
(2)如图②,试说明与的大小关系.
参考答案:
1.B
2.A
3.C
4.B
5.B
6.C
7.C
8.C
9.B
10.B
11.D
12.C
13.50
14.(2,﹣1).
15.
16.8
17.6
18.135°
19.8
21.(1)S△ABC=5;(2△A'B'C'为所作,点C'的坐标为(﹣3,3).
23.(1)(2)
一、单选题
1.如图,以正方形的各边为直径作半圆,若将该图形绕其中心旋转一定角度与原图形重合,则旋转角的最小度数是( )
A.45° B.90° C.135° D.180°
2.如图,已知点A,B的坐标分别是(﹣4,3)和(﹣1,4),把原点O和点A,B依次连接起来,得到△OAB,现将△OAB绕原点按逆时针方向旋转90°后,则点A的对应点的坐标为( )
A.(﹣3,﹣4) B.(﹣4,﹣3) C.(3,4) D.(4,3)
3.如图,把绕着点顺时针旋转得到,点的对应点落在边上,若,则为( )
A. B. C. D.
4.如图,在△ABC中,∠ACB=90°,∠BAC=20°,将△ABC绕点C顺时针旋转90°得到△A'B'C',点B的对应点B'在边AC上(不与点A,C重合),则∠AA'B'的度数为( )
A.20° B.25° C.30° D.45°
5.如图,若将△ABC绕点O逆时针旋转90°则顶点B的对应点B1的坐标为( )
A. B. C. D.
6.如图,把绕点C顺时针旋转得到,交于点G,若,则的度数是( )
A. B. C. D.
7.将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至的位置,点B的横坐标为2,则点的坐标为( )
A.(1,1) B.() C.(-1,1) D.()
8.如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连结
CD.若AB=4cm. 则△BCD的面积为( )
A.4 B.2 C.3 D.2
9.如图,中,,将沿轴依次以三角形三个顶点为旋转中心顺时针旋转,分别得图②,图③,则旋转到图⑩时直角顶点的坐标是( )
A. B. C. D.
10.如图,P是等边三角形内一点,且,,,以下3个结论:①;②;③;④若点P到三边的距离分别为,,,则有,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
11.如图,,射线在平面内.射线绕点从射线的反向延长线的位置出发,顺时针旋转角,已知平分,当与互余时旋转角等于( )
A.或 B.或 C.或 D.或
12.如图,平行四边形AOBC中,,,对角线AB,OC交于点P,将平行四边形AOBC绕点O逆时针旋转,每次旋转45°,则旋转2022次后点P的对应坐标为( )
A. B. C. D.
二、填空题
13.将一图形绕点O顺时针旋转70°后,再绕点O逆时针旋转120°,这时如果要使图形回到原来的位置,需要将图形绕点O按顺时针方向旋转 度.
14.如图,在平面直角坐标系中,若将△ABC绕点C顺时针旋转90°得到△A1B1C1,则点B的对应点 B1的坐标为 .
15.如图,在中,,,将绕点顺时针旋转得到,点的对应点恰好落在边上,连接,则的度数为 .
16.如图,正△ABC的边长为4,将正△ABC绕点B顺时针旋转120°得到△C'A'B,若点D为直线A'B上的一动点,则AD+CD的最小值是 .
17.如图,已知点P是等边内一点,,,.将线段AP绕点A逆时针旋转60°得到AQ,连接PQ,CQ.则的面积为 .
18.如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,则∠A′的度数为 .
19.若一次函数y=kx+8(k≠0)的图象与x轴、y轴分别交于A、B两点,当k的取值变化时,点A随之在x轴上运动,将线段AB绕点B逆时针旋转90°得到BQ,连接OQ,则OQ长的最小值是 .
三、解答题
20.如图,下列的图案是由什么基本图案经怎样的旋转得到的,把它画出来?
21.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,1),B(4,2),C(3,5).
(1)求△ABC的面积;
(2)在图中画出△ABC绕点A逆时针旋转90°得到的△A'B'C',并写出点C的对应点C'的坐标.
22.如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0).
(1)画出将ABC向上平移1个单位长度,再向右平移5个单位长度后得到的,点A、B、C的对应点分别为、、;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到的,点A、B的对应点分别为、.
23.如图,将一副直角三角尺(其中,)的直角顶点C叠放在一起.保持三角尺BCE不动,三角尺ACD的CD边与CB边重合,然后将三角尺ACD绕点C按逆时针方向转动,形成.
(1)如图①,当时,吗?为什么?
(2)如图②,试说明与的大小关系.
参考答案:
1.B
2.A
3.C
4.B
5.B
6.C
7.C
8.C
9.B
10.B
11.D
12.C
13.50
14.(2,﹣1).
15.
16.8
17.6
18.135°
19.8
21.(1)S△ABC=5;(2△A'B'C'为所作,点C'的坐标为(﹣3,3).
23.(1)(2)
同课章节目录
