八年级数学上册苏科版试题 第3章勾股定理 单元测试卷(含答案)
文档属性
| 名称 | 八年级数学上册苏科版试题 第3章勾股定理 单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 163.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 21:26:00 | ||
图片预览


文档简介
第3章勾股定理单元测试卷
一、选择题(本大题共8小题,每小题2分,共16分).
1.如图,在△ABC中,AB=AC=10,AD是角平分线,AD=6,则BC的长度为( )
A.6 B.8 C.12 D.16
2.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
3.如图,正方形ABCD的面积是( )
A.5 B.25 C.7 D.1
4.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列条件中,能判断△ABC是直角三角形的是( )
A.a=2,b=3,c=4 B.a:b:c
C.∠A+∠B=2∠C D.∠A=2∠B=3∠C
5.已知直角三角形纸片的两条直角边长分别为m和n(m<n),过锐角顶点把该纸片剪成两个三角形.若这两个三角形都是等腰三角形,则( )
A.﹣3m2+2mn+n2=0 B.m2+2mn﹣n2=0
C.2m2﹣2mn+n2=0 D.3m2﹣mn﹣n2=0
6.《九章算术》是我国古代的数学名著,书中的“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,问折断处离地面的高度是多少?设折断后离地面的高度为x尺,则可列方程为( )
A.x2﹣3=(10﹣x)2 B.x2﹣32=(10﹣x)2
C.x2+3=(10﹣x)2 D.x2+32=(10﹣x)2
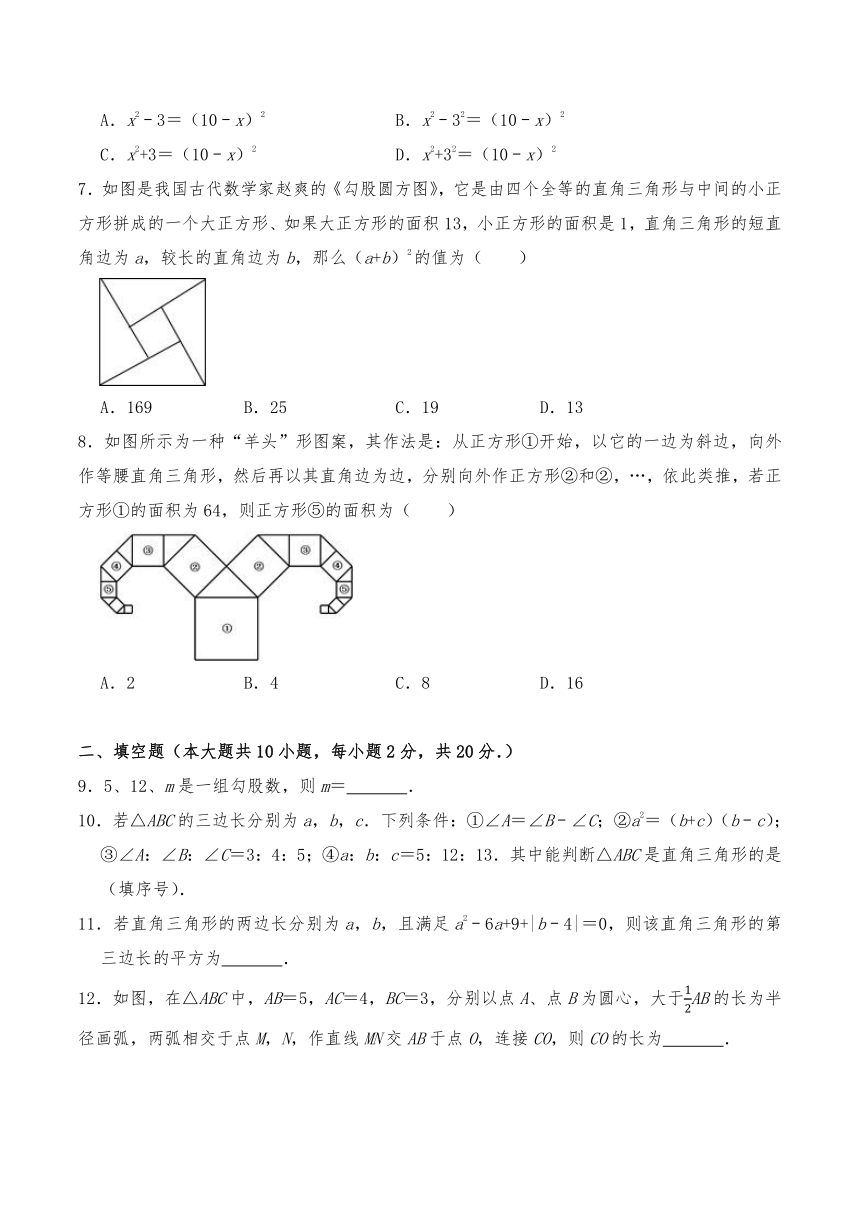
7.如图是我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形、如果大正方形的面积13,小正方形的面积是1,直角三角形的短直角边为a,较长的直角边为b,那么(a+b)2的值为( )
A.169 B.25 C.19 D.13
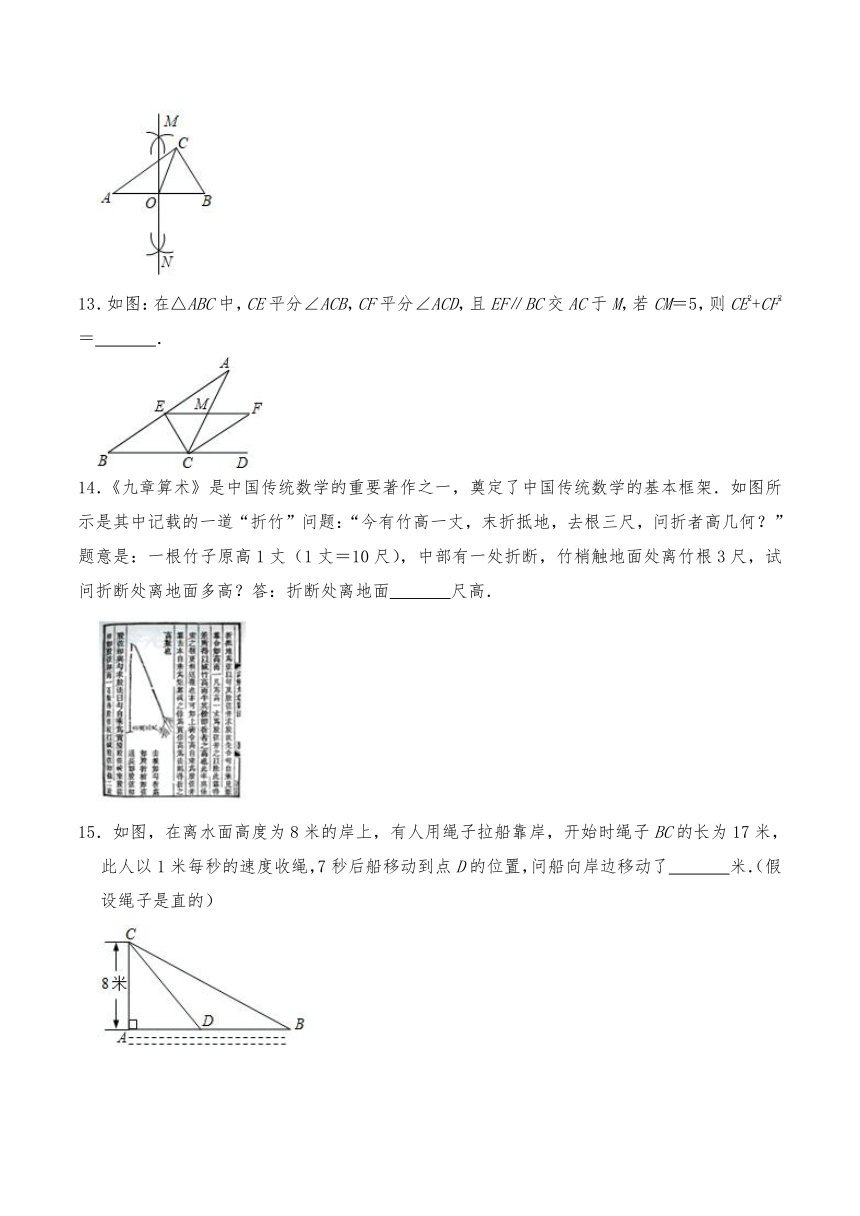
8.如图所示为一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②,…,依此类推,若正方形①的面积为64,则正方形⑤的面积为( )
A.2 B.4 C.8 D.16
二、填空题(本大题共10小题,每小题2分,共20分.)
9.5、12、m是一组勾股数,则m= .
10.若△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判断△ABC是直角三角形的是 (填序号).
11.若直角三角形的两边长分别为a,b,且满足a2﹣6a+9+|b﹣4|=0,则该直角三角形的第三边长的平方为 .
12.如图,在△ABC中,AB=5,AC=4,BC=3,分别以点A、点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,连接CO,则CO的长为 .
13.如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2= .
14.《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面 尺高.
15.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点D的位置,问船向岸边移动了 米.(假设绳子是直的)
16.如图,△ABC为等边三角形,BD⊥AB,BD=AB,则∠DCB= °.
17.如图,在等腰△ABC中,AB=AC=10,高BD=8,AE平分∠BAC,则△ABE的面积为 .
18.如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t= s时,△PBQ为直角三角形.
三、解答题(本大题共9小题,共64分.)
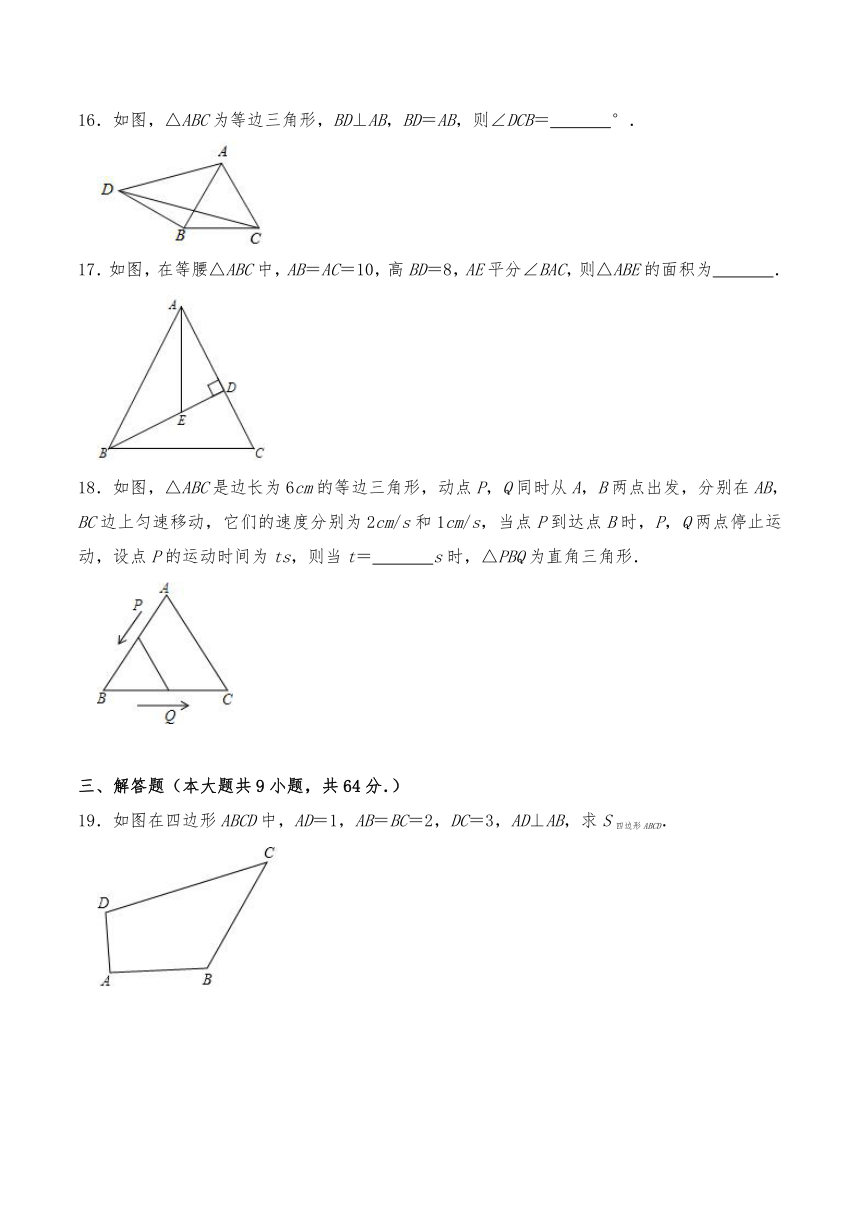
19.如图在四边形ABCD中,AD=1,AB=BC=2,DC=3,AD⊥AB,求S四边形ABCD.
20.如图,某工厂C前面有一条笔直的公路,原来有两条路AC,BC可以从工厂C到达公路,经测量AC=6千米,BC=8千米,AB=10千米,现需要修建一条路,使工厂C到公路的路程最短.请你帮工厂C设计一种方案,并求出新建路的长.
21.如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长;
(2)若E是边AB上的动点,求线段DE的最小值.
22.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺送行,二步恰竿齐,五尺板高离地…”翻译成现代文为:如图秋千细索OA悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为一尺(AC=1尺).将它往前推进两步(EB⊥OC于点E,且EB=10尺),踏板升高到点B位置,此塔板离地五尽(BD=5尺),求秋千绳索(OA或OB)的长度.
23.如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
(1)求证:DF⊥AB;
(2)利用图中阴影部分面积完成勾股定理的证明,已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.
24.法国数学家费尔马早在17世纪就研究过形如x2+y2=z2的方程,显然,这个方程有无数组解.我们把满足该方程的正整数的解(x,y,z)叫做勾股数,如(3,4,5)就是一组勾股数.
(1)在研究勾股数时,古希腊的哲学家柏拉图曾指出:如果n表示大于1的整数,x=2n,y=n2﹣1,z=n2+1,那么,以x,y,z为三边的三角形为直角三角形(即x,y,z为勾股数),请你加以证明;
(2)探索规律:观察下列各组数(3,4,5),(5,12,13),(7,24,25),(9,40,41)…,直接写出第6个数组.
25.如图,在Rt△ABC中,AB=3,BC=4,动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P,Q的运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止运动,连接PQ,设它们的运动时间为t(t>0)秒.
(1)设△CBQ的面积为S,请用含有t的代数式来表示S;
(2)线段PQ的垂直平分线记为直线l,当直线l经过点C时,求AQ的长.
26.[阅读理解]
勾股定理是几何学中一颗光彩夺目的明珠.她反映了直角三角形的三边关系即直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦“边长的平方.也就是说,设直角三角形两直角边为a和b,斜边为c,那么a2+b2=c2.迄今为止,全世界发现勾股定理的证明方法约有400种.如:美国第二十任总统伽菲尔德的“总统证法”(如图1),利用三个直角三角形拼成一个直角梯形,于是直角梯形的面积可以表示为(a+b)2或者是2abc2,因此得到(a+b)2=2abc2,运用乘法公式展开整理得到a2+b2=c2.
[尝试探究]
(1)其实我国古人早就运用各种方法证明勾股定理,如图2用四个直角三角形拼成正方形,中间也是一个正方形.其中四个直角三角形直角边分别为a、b,斜边长为c,请你根据古人的拼图完成证明.
(2)图3是2002年在中国北京召开的国际数学家大会会标,利用此图也能证明勾股定理,其中四个直角三角形直角边分别为a、b,斜边长为c,请你帮助完成.
[实践应用]
已知a、b、c为Rt△ABC的三边(c>b>a),试比较代数式a2c2+a2b2与c4﹣b4的大小关系.
27.如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上(但不与A点重合),求t的值.
答案
一、选择题
D.A.B.B.B.D.B.B.
二、填空题
9.13.
10.①②④.
11.7或25.
12..
13.100.
14.4.55.
15.9.
16.15.
17.15.
18.或.
三、解答题
19.连接BD,
∵AD⊥AB,
∴∠A=90°,
由勾股定理得:BD,
∵在△DBC中,BC=2,DB,DC=3,
∴BD2+BC2=DC2,
∴∠DBC=90°,
∴S四边形ABCD=S△DAB+S△DBC2=1.
20.过点C作CD⊥AB于点D,则线段CD为新建公路.
∵AC=6km,BC=8km,AB=10km
∴AC2+BC2=62+82=100,AB2=102=100,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
∵S△ABC AC BCAB CD,
∴6×810×CD,∴CD=4.8km
∴新建路的长为4.8km.
21.(1)在△BCD中,BC=13,BD=12,CD=AC﹣AD=5,
∵52+122=169=132,即CD2+BD2=BC2,
∴∠BDC=90°.
在Rt△ABD中,AD=16,BD=12,∠ADB=90°,
∴AB20.
又∵点E是边AB的中点,
∴DEAB=10.
(2)当DE⊥AB时,DE长度最小.
此时:S△ABDAD BDAB DE,
∴DE.
∴线段DE的最小值为.
22.设OB=OA=x(尺),
∵四边形BECD是矩形,
∴BD=EC=5(尺),
在Rt△OBE中,OB=x,OE=x﹣4,BE=10,
∴x2=102+(x﹣4)2,
∴x.
∴OA的长度为(尺).
23.(1)∵AC⊥BD,∠CAD=45°,
∴AC=DC,∠ACB=∠DCE=90°,
在Rt△ABC与Rt△DEC中,
,
∴Rt△ABC≌Rt△DEC(HL),
∴∠BAC=∠EDC,
∵∠EDC+∠CED=90°,∠CED=∠AEF,
∴∠AEF+∠BAC=90°,
∴∠AFE=90°,
∴DF⊥AB.
(2)∵S△BCE+S△ACD=S△ABD﹣S△ABE,
∴a2b2 c DF c EF c (DF﹣EF) c DEc2,
∴a2+b2=c2.
24.(1)证明:x2+y2
=(2n)2+(n2﹣1)2
=4n2+n4﹣2n2+1
=n4+2n2+1
=(n2+1)2
=z2,
即x,y,z为勾股数.
(2)∵①3=2×1+1,4=2×12+2×1,5=2×12+2×1+1;
②5=2×2+1,12=2×22+2×2,13=2×22+2×2+1;
③7=2×3+1,24=2×32+2×3,25=2×32+2×3+1;
④9=2×4+1,40=2×42+2×4,41=2×42+2×4+1;
⑤11=2×5+1,60=2×52+2×5,61=2×52+2×5+1,
则⑥13=2×6+1,2×62+2×6=84,2×62+2×6+1=85,
∴第6组勾股数是:(13,84,85).
25.(1)如图1,当0<t≤3时,
BQ=t,BC=4,
∴S4×t=2t;
如图2,当3<t≤5时,
,
AQ=t﹣3,
则BQ=3﹣(t﹣3)=6﹣t,
∴S4×(6﹣t)=12﹣2t;
(2)连接CQ,如图3,
∵QP的垂直平分线过点C,
∴CP=CQ,∵AB=3,BC=4,∴AC5,
∴42+t2=(5﹣t)2,解得t;
或42+(6﹣t)2=(5﹣t)2,显然不成立;
∴AQ=3.
26.[尝试探究](1)图中大正方形的面积可表示为(a+b)2,也可表示为c2+4(ab),即(a+b)2=c2+4(ab),
∴a2+b2=c2;
(2)图中大正方形的面积可表示为c2,也可表示为(b﹣a)2+4(ab),即(b﹣a)2+4(ab)=c2,
∴a2+b2=c2;
[实践应用]∵a2c2+a2b2=a2(c2+b2),c4﹣b4=(c2+b2)(c2﹣b2)=(c2+b2)a2,
∴代数式a2c2+a2b2与c4﹣b4的大小关系是相等.
27.(1)在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,
则由勾股定理得到:AC8(cm)
设存在点P,使得PA=PB,
此时PA=PB=t,PC=8﹣t,
在Rt△PCB中,PC2+CB2=PB2,
即:(8﹣t)2+62=t2,
解得:t,
∴当t时,PA=PB;
(2)当点P在∠BAC的平分线上时,如图,过点P作PE⊥AB于点E,
此时BP=14﹣t,PE=PC=t﹣8,BE=10﹣8=2,
在Rt△BEP中,PE2+BE2=BP2,
即:(t﹣8)2+22=(14﹣t)2,
解得:t,
∴当t时,P在△ABC的角平分线上.
一、选择题(本大题共8小题,每小题2分,共16分).
1.如图,在△ABC中,AB=AC=10,AD是角平分线,AD=6,则BC的长度为( )
A.6 B.8 C.12 D.16
2.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
3.如图,正方形ABCD的面积是( )
A.5 B.25 C.7 D.1
4.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列条件中,能判断△ABC是直角三角形的是( )
A.a=2,b=3,c=4 B.a:b:c
C.∠A+∠B=2∠C D.∠A=2∠B=3∠C
5.已知直角三角形纸片的两条直角边长分别为m和n(m<n),过锐角顶点把该纸片剪成两个三角形.若这两个三角形都是等腰三角形,则( )
A.﹣3m2+2mn+n2=0 B.m2+2mn﹣n2=0
C.2m2﹣2mn+n2=0 D.3m2﹣mn﹣n2=0
6.《九章算术》是我国古代的数学名著,书中的“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,问折断处离地面的高度是多少?设折断后离地面的高度为x尺,则可列方程为( )
A.x2﹣3=(10﹣x)2 B.x2﹣32=(10﹣x)2
C.x2+3=(10﹣x)2 D.x2+32=(10﹣x)2
7.如图是我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形、如果大正方形的面积13,小正方形的面积是1,直角三角形的短直角边为a,较长的直角边为b,那么(a+b)2的值为( )
A.169 B.25 C.19 D.13
8.如图所示为一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②,…,依此类推,若正方形①的面积为64,则正方形⑤的面积为( )
A.2 B.4 C.8 D.16
二、填空题(本大题共10小题,每小题2分,共20分.)
9.5、12、m是一组勾股数,则m= .
10.若△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判断△ABC是直角三角形的是 (填序号).
11.若直角三角形的两边长分别为a,b,且满足a2﹣6a+9+|b﹣4|=0,则该直角三角形的第三边长的平方为 .
12.如图,在△ABC中,AB=5,AC=4,BC=3,分别以点A、点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,连接CO,则CO的长为 .
13.如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2= .
14.《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面 尺高.
15.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点D的位置,问船向岸边移动了 米.(假设绳子是直的)
16.如图,△ABC为等边三角形,BD⊥AB,BD=AB,则∠DCB= °.
17.如图,在等腰△ABC中,AB=AC=10,高BD=8,AE平分∠BAC,则△ABE的面积为 .
18.如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t= s时,△PBQ为直角三角形.
三、解答题(本大题共9小题,共64分.)
19.如图在四边形ABCD中,AD=1,AB=BC=2,DC=3,AD⊥AB,求S四边形ABCD.
20.如图,某工厂C前面有一条笔直的公路,原来有两条路AC,BC可以从工厂C到达公路,经测量AC=6千米,BC=8千米,AB=10千米,现需要修建一条路,使工厂C到公路的路程最短.请你帮工厂C设计一种方案,并求出新建路的长.
21.如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长;
(2)若E是边AB上的动点,求线段DE的最小值.
22.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺送行,二步恰竿齐,五尺板高离地…”翻译成现代文为:如图秋千细索OA悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为一尺(AC=1尺).将它往前推进两步(EB⊥OC于点E,且EB=10尺),踏板升高到点B位置,此塔板离地五尽(BD=5尺),求秋千绳索(OA或OB)的长度.
23.如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
(1)求证:DF⊥AB;
(2)利用图中阴影部分面积完成勾股定理的证明,已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.
24.法国数学家费尔马早在17世纪就研究过形如x2+y2=z2的方程,显然,这个方程有无数组解.我们把满足该方程的正整数的解(x,y,z)叫做勾股数,如(3,4,5)就是一组勾股数.
(1)在研究勾股数时,古希腊的哲学家柏拉图曾指出:如果n表示大于1的整数,x=2n,y=n2﹣1,z=n2+1,那么,以x,y,z为三边的三角形为直角三角形(即x,y,z为勾股数),请你加以证明;
(2)探索规律:观察下列各组数(3,4,5),(5,12,13),(7,24,25),(9,40,41)…,直接写出第6个数组.
25.如图,在Rt△ABC中,AB=3,BC=4,动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P,Q的运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止运动,连接PQ,设它们的运动时间为t(t>0)秒.
(1)设△CBQ的面积为S,请用含有t的代数式来表示S;
(2)线段PQ的垂直平分线记为直线l,当直线l经过点C时,求AQ的长.
26.[阅读理解]
勾股定理是几何学中一颗光彩夺目的明珠.她反映了直角三角形的三边关系即直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦“边长的平方.也就是说,设直角三角形两直角边为a和b,斜边为c,那么a2+b2=c2.迄今为止,全世界发现勾股定理的证明方法约有400种.如:美国第二十任总统伽菲尔德的“总统证法”(如图1),利用三个直角三角形拼成一个直角梯形,于是直角梯形的面积可以表示为(a+b)2或者是2abc2,因此得到(a+b)2=2abc2,运用乘法公式展开整理得到a2+b2=c2.
[尝试探究]
(1)其实我国古人早就运用各种方法证明勾股定理,如图2用四个直角三角形拼成正方形,中间也是一个正方形.其中四个直角三角形直角边分别为a、b,斜边长为c,请你根据古人的拼图完成证明.
(2)图3是2002年在中国北京召开的国际数学家大会会标,利用此图也能证明勾股定理,其中四个直角三角形直角边分别为a、b,斜边长为c,请你帮助完成.
[实践应用]
已知a、b、c为Rt△ABC的三边(c>b>a),试比较代数式a2c2+a2b2与c4﹣b4的大小关系.
27.如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上(但不与A点重合),求t的值.
答案
一、选择题
D.A.B.B.B.D.B.B.
二、填空题
9.13.
10.①②④.
11.7或25.
12..
13.100.
14.4.55.
15.9.
16.15.
17.15.
18.或.
三、解答题
19.连接BD,
∵AD⊥AB,
∴∠A=90°,
由勾股定理得:BD,
∵在△DBC中,BC=2,DB,DC=3,
∴BD2+BC2=DC2,
∴∠DBC=90°,
∴S四边形ABCD=S△DAB+S△DBC2=1.
20.过点C作CD⊥AB于点D,则线段CD为新建公路.
∵AC=6km,BC=8km,AB=10km
∴AC2+BC2=62+82=100,AB2=102=100,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
∵S△ABC AC BCAB CD,
∴6×810×CD,∴CD=4.8km
∴新建路的长为4.8km.
21.(1)在△BCD中,BC=13,BD=12,CD=AC﹣AD=5,
∵52+122=169=132,即CD2+BD2=BC2,
∴∠BDC=90°.
在Rt△ABD中,AD=16,BD=12,∠ADB=90°,
∴AB20.
又∵点E是边AB的中点,
∴DEAB=10.
(2)当DE⊥AB时,DE长度最小.
此时:S△ABDAD BDAB DE,
∴DE.
∴线段DE的最小值为.
22.设OB=OA=x(尺),
∵四边形BECD是矩形,
∴BD=EC=5(尺),
在Rt△OBE中,OB=x,OE=x﹣4,BE=10,
∴x2=102+(x﹣4)2,
∴x.
∴OA的长度为(尺).
23.(1)∵AC⊥BD,∠CAD=45°,
∴AC=DC,∠ACB=∠DCE=90°,
在Rt△ABC与Rt△DEC中,
,
∴Rt△ABC≌Rt△DEC(HL),
∴∠BAC=∠EDC,
∵∠EDC+∠CED=90°,∠CED=∠AEF,
∴∠AEF+∠BAC=90°,
∴∠AFE=90°,
∴DF⊥AB.
(2)∵S△BCE+S△ACD=S△ABD﹣S△ABE,
∴a2b2 c DF c EF c (DF﹣EF) c DEc2,
∴a2+b2=c2.
24.(1)证明:x2+y2
=(2n)2+(n2﹣1)2
=4n2+n4﹣2n2+1
=n4+2n2+1
=(n2+1)2
=z2,
即x,y,z为勾股数.
(2)∵①3=2×1+1,4=2×12+2×1,5=2×12+2×1+1;
②5=2×2+1,12=2×22+2×2,13=2×22+2×2+1;
③7=2×3+1,24=2×32+2×3,25=2×32+2×3+1;
④9=2×4+1,40=2×42+2×4,41=2×42+2×4+1;
⑤11=2×5+1,60=2×52+2×5,61=2×52+2×5+1,
则⑥13=2×6+1,2×62+2×6=84,2×62+2×6+1=85,
∴第6组勾股数是:(13,84,85).
25.(1)如图1,当0<t≤3时,
BQ=t,BC=4,
∴S4×t=2t;
如图2,当3<t≤5时,
,
AQ=t﹣3,
则BQ=3﹣(t﹣3)=6﹣t,
∴S4×(6﹣t)=12﹣2t;
(2)连接CQ,如图3,
∵QP的垂直平分线过点C,
∴CP=CQ,∵AB=3,BC=4,∴AC5,
∴42+t2=(5﹣t)2,解得t;
或42+(6﹣t)2=(5﹣t)2,显然不成立;
∴AQ=3.
26.[尝试探究](1)图中大正方形的面积可表示为(a+b)2,也可表示为c2+4(ab),即(a+b)2=c2+4(ab),
∴a2+b2=c2;
(2)图中大正方形的面积可表示为c2,也可表示为(b﹣a)2+4(ab),即(b﹣a)2+4(ab)=c2,
∴a2+b2=c2;
[实践应用]∵a2c2+a2b2=a2(c2+b2),c4﹣b4=(c2+b2)(c2﹣b2)=(c2+b2)a2,
∴代数式a2c2+a2b2与c4﹣b4的大小关系是相等.
27.(1)在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,
则由勾股定理得到:AC8(cm)
设存在点P,使得PA=PB,
此时PA=PB=t,PC=8﹣t,
在Rt△PCB中,PC2+CB2=PB2,
即:(8﹣t)2+62=t2,
解得:t,
∴当t时,PA=PB;
(2)当点P在∠BAC的平分线上时,如图,过点P作PE⊥AB于点E,
此时BP=14﹣t,PE=PC=t﹣8,BE=10﹣8=2,
在Rt△BEP中,PE2+BE2=BP2,
即:(t﹣8)2+22=(14﹣t)2,
解得:t,
∴当t时,P在△ABC的角平分线上.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
