八年级数学上册苏科版试题 第2章轴对称图形单元测试(含答案)
文档属性
| 名称 | 八年级数学上册苏科版试题 第2章轴对称图形单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 162.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 21:27:23 | ||
图片预览




文档简介
第2章轴对称图形单元测试
一、选择题(本大题共8小题,每小题2分,共16分).
1.下列几何图形不一定是轴对称图形的是( )
A.三角形 B.长方形 C.正五边形 D.圆
2.下列说法中,正确的是( )
A.线段是轴对称图形,对称轴是线段的垂直平分线
B.等腰三角形至少有1条对称轴,至多有3条对称轴
C.全等的两个三角形一定关于某直线对称
D.两图形关于某直线对称,对称点一定在直线的两旁
3.一个等腰三角形的两边长分别是2cm和5cm,则它的周长为( )
A.9cm B.12cm C.7cm D.9cm或12cm
4.如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC,分别交AB、AC于点D、E,那么下列结论:①△BDF和△CEF都是等腰三角形;②F为DE中点;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的有( )
A.①③ B.①②③ C.①② D.①④
5.如图,已知OC平分∠AOB,P是OC上一点,PH⊥OB于H,若PH=5,则点P与射线OA上某一点连线的长度可以是( )
A.6 B.4 C.3 D.2
6.如图,已知△ABC中,∠ABC=40°,∠ACB=60°,DE垂直平分AC,连接AE,则∠BAE的度数是( )
A.10° B.15° C.20° D.25°
7.如图,∠MON=90°,已知△ABC中,AC=BC=AB=6,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的距离为整数的点有( )个.
A.5 B.6 C.7 D.8
8.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF,根据图中标示的角度,∠EAF的度数为( )
A.126° B.128° C.130° D.132°
二、填空题(本大题共10小题,每小题2分,共20分.)
9.如图,在三角形纸片ABC中剪去∠C得到四边形ABDE,且∠C=40°,则∠1+∠2的度数为 .
10.直角三角形中,两直角边长分别为2和4,则斜边上的中线长为 .
11.如果实数a、b满足|a﹣2|+(b﹣4)2=0,且a、b恰好是等腰△ABC的两边长,则△ABC的周长是 .
12.如图,在△ABC中,AB=AC,∠DBC=28°,且BD⊥AC,则∠A= °.
13.在等腰三角形ABC中,∠A=2∠B,则∠C的度数为 .
14.如图,在△ABC中,AB=10,AC=8,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.则△AMN的周长为 .
15.如图△ABC中,AB的垂直平分线交BC于D,AD=5,BC=11,则DC= .
16.△ABC中,最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,如图为其中一种分割法,此时△ABC中的最大内角为90°,那么其它分割法中,△ABC中的最大内角度数为 .
17.Rt△ABC中,∠ACB=90°,∠A=60°,在直线BC上取一点P使得△PAB是等腰三角形,则符合条件的点P有 个.
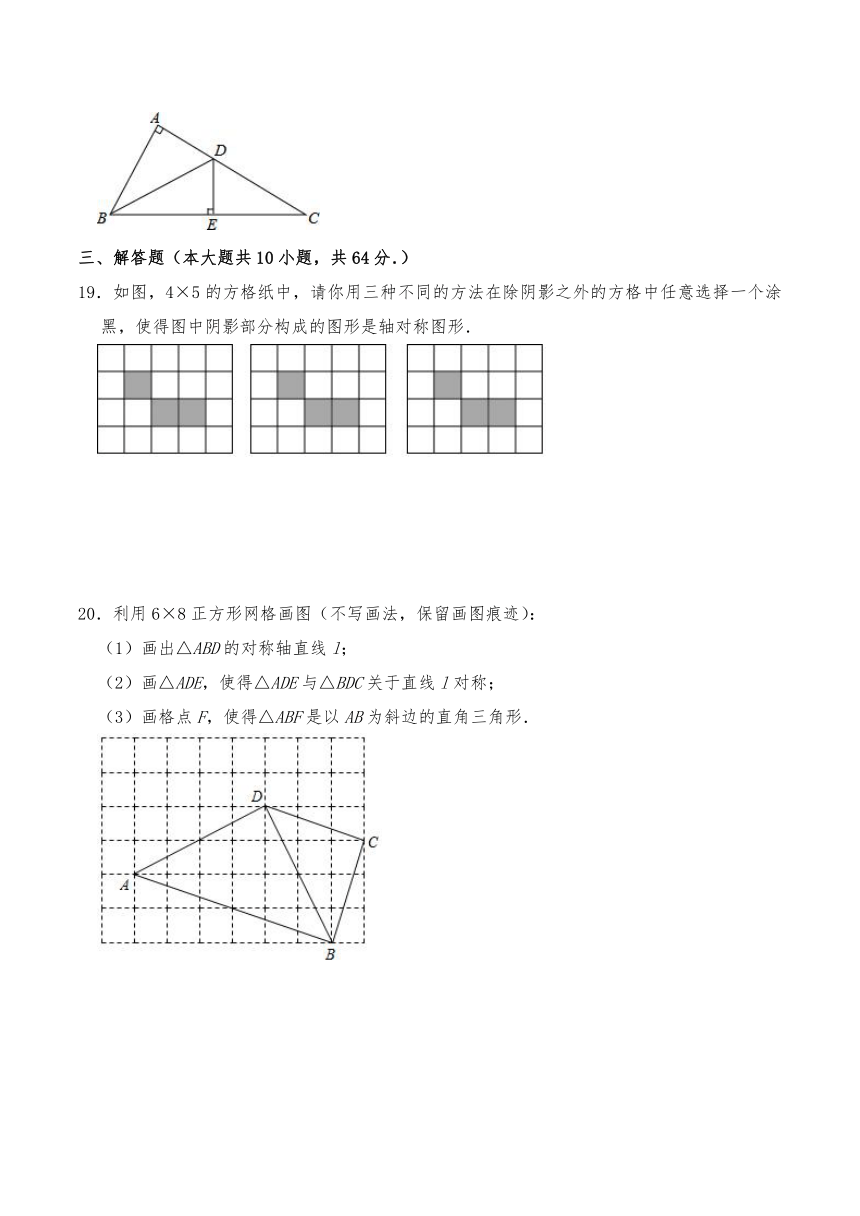
18.如图,Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,DE垂直平分BC,垂足为E,则∠C的度数为 °.
三、解答题(本大题共10小题,共64分.)
19.如图,4×5的方格纸中,请你用三种不同的方法在除阴影之外的方格中任意选择一个涂黑,使得图中阴影部分构成的图形是轴对称图形.
20.利用6×8正方形网格画图(不写画法,保留画图痕迹):
(1)画出△ABD的对称轴直线l;
(2)画△ADE,使得△ADE与△BDC关于直线l对称;
(3)画格点F,使得△ABF是以AB为斜边的直角三角形.
21.方格纸中每个小方格都的边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.
(1)在图1中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形;
(2)在图2中画一个格点正方形,使其面积等于10;
(3)直接写出图3中△FGH的面积是 .
22.如图:在△ABC中,∠B=90°,AB=BD,AD=CD,求∠CAD的度数.
23.已知:如图,在△ABC中,∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,垂足分别为E、F.
(1)求证:PE=PF;
(2)若∠BAC=60°,连接AP,求∠EAP的度数.
24.如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若AB=21cm,则△CMN的周长= ;(第一问直接写答案)
(2)若∠MFN=80°,求∠MCN的度数.
25.如图,三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,求△ADE的周长.
26.如图,在△ABC中,∠ABC=70°,∠A=∠C,EF∥BD,∠1=∠2.
求:(1)∠C的度数;
(2)∠ADG的度数.
27.(1)如图1,△ABC中,作∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E.F.
①求证:OE=BE;
②若△ABC的周长是25,BC=9,试求出△AEF的周长;
(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,若∠BAC=80°.∠PAC的度数
28.如图,在△ABC中,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)若∠BAC=90°(图1),求∠DAE的度数;
(2)若∠BAC=120°(图2),求∠DAE的度数;
(3)当∠BAC>90°时,探求∠DAE与∠BAC之间的数量关系,直接写出结果.
答案
一、选择题
A.B.B.A.A.C.B.D.
二、填空题
9.220°.
10..
11.10.
12.56.
13.45°或72°.
14.18.
15.6.
16.117°或108°或84°.
17.4.
18.30
三、解答题
19.如图所示:
.
20.(1)如图所示,直线l即为所求.
(2)如图所示,△ADE即为所求;
(3)如图所示,点F即为所求.
21.(1)如图1所示:
(2)如图2所示:
(3)如图3所示:
△FGH的面积=矩形ABHC的面积﹣△AFG的面积﹣△BGH的面积﹣△FCH的面积
=5×6
=9
故答案为:9.
22.∵△ABC中,∠B=90°,AB=BD,AD=CD
∴∠BAD=∠ADB=45°,∠DCA=∠CAD
∴∠BDA=2∠CAD=45°
∴∠CAD=22.5°
23.(1)过点P作PD⊥BC于D,
∵∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,
∴PD=PE,PD=PF,
∴PE=PF;
(2)∵PE=PF,PE⊥AB,PF⊥AC,
∴AP平分∠BAC,
∵∠BAC=60°,
∴∠EAP30°.
24.(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB=21cm,
故答案为:21cm;
(2)∵∠MFN=80°,
∴∠MNF+∠NMF=180°﹣80°=100°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=100°,
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣100°=80°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°﹣2(∠A+∠B)=180°﹣2×80°=20°.
25.∵折叠这个三角形点C落在AB边上的点E处,折痕为BD,
∴BE=BC,DE=CD,
∴AE=AB﹣BE=AB﹣BC=8﹣6=2cm,
∴△ADE的周长=AD+DE+AE,
=AD+CD+AE,
=AC+AE,
=5+2,
=7cm.
26.(1)∵∠A+∠ABC+∠C=180°,∠ABC=70°,
∴∠A+∠C=110°,
∵∠A=∠C,
∴∠C=55°;
(2)∵EF∥BD,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴DG∥BC,
∴∠ADG=∠C=55°.
27.(1)①∵BO平分∠ABC,
∴∠EBO=∠OBC,
∵EF∥BC,
∴∠EOB=∠OBC,
∴∠EOB=∠EBO,
∴OE=BE;
②△AEF的周长=AE+AF+EF=AE+AF+EB+FC=AB+AC=25﹣9=16;
(2)解:延长BA,做PN⊥BD,PF⊥BA,PM⊥AC,
∵CP平分∠ACD,
∴∠ACP=∠PCD,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∴∠FAP=∠PAC,
∴∠FAC=2∠PAC,
∵∠FAC+∠BAC=180°,
∴2∠PAC+∠BAC=180°,
∴∠PAC(180°﹣∠BAC)(180°﹣80°)=50°.
28.(1)如图1,∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA(180°﹣∠B)=67.5°,
∵CE=CA,
∴∠CAE=∠E∠ACB=22.5°,
∴∠BAE=180°﹣∠B﹣∠E=112.5°,
∴∠DAE=∠BAE﹣∠BAD=45°,
(2)如图2,∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=30°,
∵BA=BD,
∴∠BAD=∠BDA=75°,
∴∠DAC=45°,
∵CA=CE,
∴∠E=∠CAE=15°,
∴∠DAE=∠DAC+∠CAE=60°;
(3)∠DAE∠BAC,
理由:设∠CAE=x,∠BAD=y,
则∠B=180°﹣2y,∠E=∠CAE=x,
∴∠BAE=180°﹣∠B﹣∠E=2y﹣x,
∴∠DAE=∠BAE﹣∠BAD=2y﹣x﹣y=y﹣x,
∠BAC=∠BAE﹣∠CAE=2y﹣x﹣x=2y﹣2x
∴∠DAE∠BAC.
一、选择题(本大题共8小题,每小题2分,共16分).
1.下列几何图形不一定是轴对称图形的是( )
A.三角形 B.长方形 C.正五边形 D.圆
2.下列说法中,正确的是( )
A.线段是轴对称图形,对称轴是线段的垂直平分线
B.等腰三角形至少有1条对称轴,至多有3条对称轴
C.全等的两个三角形一定关于某直线对称
D.两图形关于某直线对称,对称点一定在直线的两旁
3.一个等腰三角形的两边长分别是2cm和5cm,则它的周长为( )
A.9cm B.12cm C.7cm D.9cm或12cm
4.如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC,分别交AB、AC于点D、E,那么下列结论:①△BDF和△CEF都是等腰三角形;②F为DE中点;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的有( )
A.①③ B.①②③ C.①② D.①④
5.如图,已知OC平分∠AOB,P是OC上一点,PH⊥OB于H,若PH=5,则点P与射线OA上某一点连线的长度可以是( )
A.6 B.4 C.3 D.2
6.如图,已知△ABC中,∠ABC=40°,∠ACB=60°,DE垂直平分AC,连接AE,则∠BAE的度数是( )
A.10° B.15° C.20° D.25°
7.如图,∠MON=90°,已知△ABC中,AC=BC=AB=6,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的距离为整数的点有( )个.
A.5 B.6 C.7 D.8
8.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF,根据图中标示的角度,∠EAF的度数为( )
A.126° B.128° C.130° D.132°
二、填空题(本大题共10小题,每小题2分,共20分.)
9.如图,在三角形纸片ABC中剪去∠C得到四边形ABDE,且∠C=40°,则∠1+∠2的度数为 .
10.直角三角形中,两直角边长分别为2和4,则斜边上的中线长为 .
11.如果实数a、b满足|a﹣2|+(b﹣4)2=0,且a、b恰好是等腰△ABC的两边长,则△ABC的周长是 .
12.如图,在△ABC中,AB=AC,∠DBC=28°,且BD⊥AC,则∠A= °.
13.在等腰三角形ABC中,∠A=2∠B,则∠C的度数为 .
14.如图,在△ABC中,AB=10,AC=8,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.则△AMN的周长为 .
15.如图△ABC中,AB的垂直平分线交BC于D,AD=5,BC=11,则DC= .
16.△ABC中,最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,如图为其中一种分割法,此时△ABC中的最大内角为90°,那么其它分割法中,△ABC中的最大内角度数为 .
17.Rt△ABC中,∠ACB=90°,∠A=60°,在直线BC上取一点P使得△PAB是等腰三角形,则符合条件的点P有 个.
18.如图,Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,DE垂直平分BC,垂足为E,则∠C的度数为 °.
三、解答题(本大题共10小题,共64分.)
19.如图,4×5的方格纸中,请你用三种不同的方法在除阴影之外的方格中任意选择一个涂黑,使得图中阴影部分构成的图形是轴对称图形.
20.利用6×8正方形网格画图(不写画法,保留画图痕迹):
(1)画出△ABD的对称轴直线l;
(2)画△ADE,使得△ADE与△BDC关于直线l对称;
(3)画格点F,使得△ABF是以AB为斜边的直角三角形.
21.方格纸中每个小方格都的边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.
(1)在图1中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形;
(2)在图2中画一个格点正方形,使其面积等于10;
(3)直接写出图3中△FGH的面积是 .
22.如图:在△ABC中,∠B=90°,AB=BD,AD=CD,求∠CAD的度数.
23.已知:如图,在△ABC中,∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,垂足分别为E、F.
(1)求证:PE=PF;
(2)若∠BAC=60°,连接AP,求∠EAP的度数.
24.如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若AB=21cm,则△CMN的周长= ;(第一问直接写答案)
(2)若∠MFN=80°,求∠MCN的度数.
25.如图,三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,求△ADE的周长.
26.如图,在△ABC中,∠ABC=70°,∠A=∠C,EF∥BD,∠1=∠2.
求:(1)∠C的度数;
(2)∠ADG的度数.
27.(1)如图1,△ABC中,作∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E.F.
①求证:OE=BE;
②若△ABC的周长是25,BC=9,试求出△AEF的周长;
(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,若∠BAC=80°.∠PAC的度数
28.如图,在△ABC中,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)若∠BAC=90°(图1),求∠DAE的度数;
(2)若∠BAC=120°(图2),求∠DAE的度数;
(3)当∠BAC>90°时,探求∠DAE与∠BAC之间的数量关系,直接写出结果.
答案
一、选择题
A.B.B.A.A.C.B.D.
二、填空题
9.220°.
10..
11.10.
12.56.
13.45°或72°.
14.18.
15.6.
16.117°或108°或84°.
17.4.
18.30
三、解答题
19.如图所示:
.
20.(1)如图所示,直线l即为所求.
(2)如图所示,△ADE即为所求;
(3)如图所示,点F即为所求.
21.(1)如图1所示:
(2)如图2所示:
(3)如图3所示:
△FGH的面积=矩形ABHC的面积﹣△AFG的面积﹣△BGH的面积﹣△FCH的面积
=5×6
=9
故答案为:9.
22.∵△ABC中,∠B=90°,AB=BD,AD=CD
∴∠BAD=∠ADB=45°,∠DCA=∠CAD
∴∠BDA=2∠CAD=45°
∴∠CAD=22.5°
23.(1)过点P作PD⊥BC于D,
∵∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,
∴PD=PE,PD=PF,
∴PE=PF;
(2)∵PE=PF,PE⊥AB,PF⊥AC,
∴AP平分∠BAC,
∵∠BAC=60°,
∴∠EAP30°.
24.(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB=21cm,
故答案为:21cm;
(2)∵∠MFN=80°,
∴∠MNF+∠NMF=180°﹣80°=100°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=100°,
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣100°=80°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°﹣2(∠A+∠B)=180°﹣2×80°=20°.
25.∵折叠这个三角形点C落在AB边上的点E处,折痕为BD,
∴BE=BC,DE=CD,
∴AE=AB﹣BE=AB﹣BC=8﹣6=2cm,
∴△ADE的周长=AD+DE+AE,
=AD+CD+AE,
=AC+AE,
=5+2,
=7cm.
26.(1)∵∠A+∠ABC+∠C=180°,∠ABC=70°,
∴∠A+∠C=110°,
∵∠A=∠C,
∴∠C=55°;
(2)∵EF∥BD,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴DG∥BC,
∴∠ADG=∠C=55°.
27.(1)①∵BO平分∠ABC,
∴∠EBO=∠OBC,
∵EF∥BC,
∴∠EOB=∠OBC,
∴∠EOB=∠EBO,
∴OE=BE;
②△AEF的周长=AE+AF+EF=AE+AF+EB+FC=AB+AC=25﹣9=16;
(2)解:延长BA,做PN⊥BD,PF⊥BA,PM⊥AC,
∵CP平分∠ACD,
∴∠ACP=∠PCD,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∴∠FAP=∠PAC,
∴∠FAC=2∠PAC,
∵∠FAC+∠BAC=180°,
∴2∠PAC+∠BAC=180°,
∴∠PAC(180°﹣∠BAC)(180°﹣80°)=50°.
28.(1)如图1,∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA(180°﹣∠B)=67.5°,
∵CE=CA,
∴∠CAE=∠E∠ACB=22.5°,
∴∠BAE=180°﹣∠B﹣∠E=112.5°,
∴∠DAE=∠BAE﹣∠BAD=45°,
(2)如图2,∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=30°,
∵BA=BD,
∴∠BAD=∠BDA=75°,
∴∠DAC=45°,
∵CA=CE,
∴∠E=∠CAE=15°,
∴∠DAE=∠DAC+∠CAE=60°;
(3)∠DAE∠BAC,
理由:设∠CAE=x,∠BAD=y,
则∠B=180°﹣2y,∠E=∠CAE=x,
∴∠BAE=180°﹣∠B﹣∠E=2y﹣x,
∴∠DAE=∠BAE﹣∠BAD=2y﹣x﹣y=y﹣x,
∠BAC=∠BAE﹣∠CAE=2y﹣x﹣x=2y﹣2x
∴∠DAE∠BAC.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
