多边形内角和
图片预览



文档简介
课件21张PPT。
由这图形你能抽象出什么几何图形?你猜到了吗?比
一
比? 1、你能说一说什么叫三角形? 2、你能说出什么叫四边形、五边形、多边形吗? 由 条不在同一直线上的线段首尾顺次连结组成的平面图形,称为 边形。
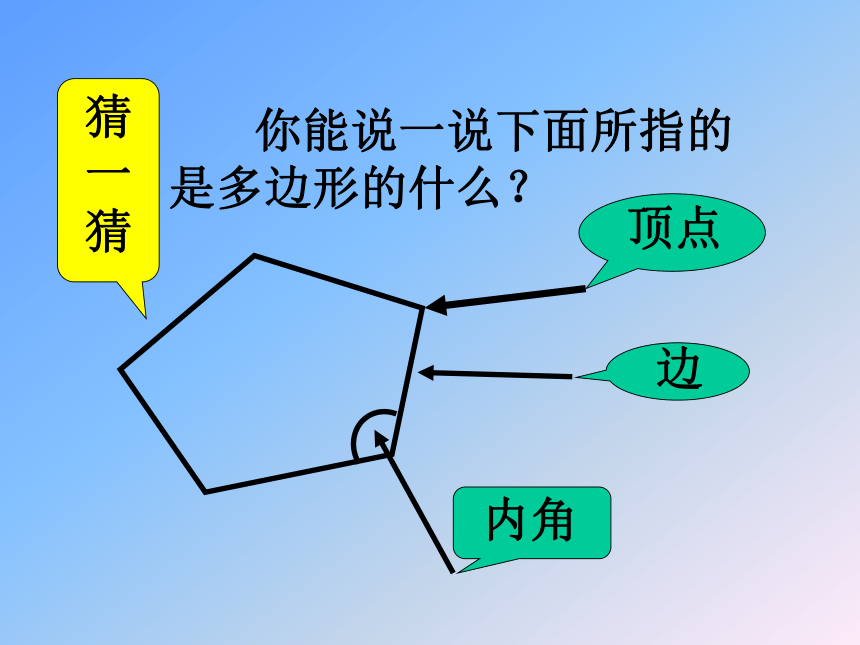
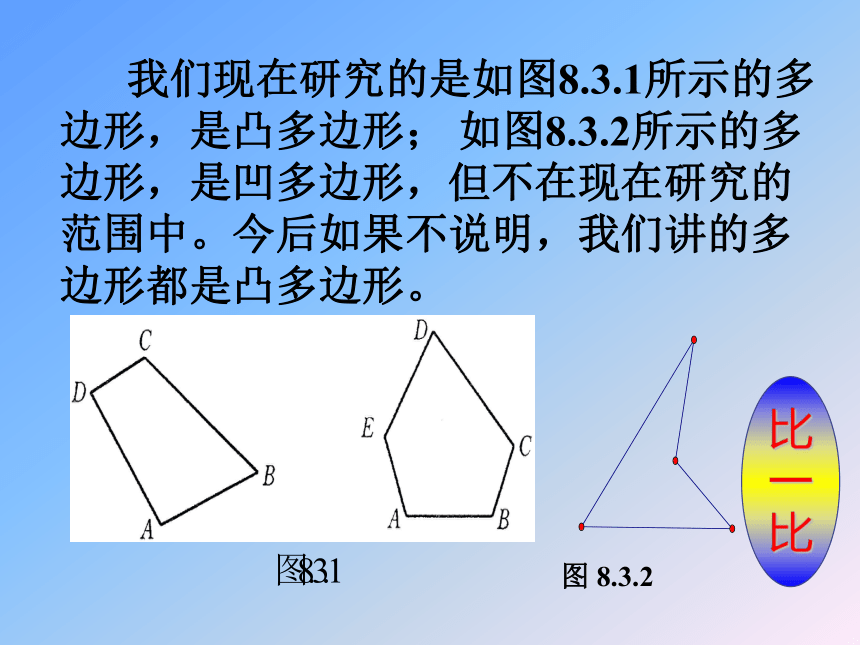
五四四五nn又称为多边形。 你能说一说下面所指的是多边形的什么? 猜一猜边内角顶点1、什么叫正三角形?什么叫正方形? 3、如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形 (regular polygon)2、什么叫正多边形?归纳: 我们现在研究的是如图8.3.1所示的多边形,是凸多边形; 如图8.3.2所示的多边形,是凹多边形,但不在现在研究的范围中。今后如果不说明,我们讲的多边形都是凸多边形。图 8.3.2比
一
比画出连结下面四点的所有线段: 连结多边形不相邻的两个顶点的线段叫做多边形的对角线。 做
一
做ABCD 你知道三角形、四边形、五边形、六边形等n边形从一个顶点所画的对角线的条数吗?在练习卷上试画一画,并填下表:??????0123n-3探索课后试一试 :你能求n边形的对角线的条数 ? 请同学们利用数学工具,先把你们手上的多边形的内角和计算出来,并完成下表.试一试议一议总结最佳方法: 通过分割成三角形,转
化为利用三角形内角和求出。 1800 3600 540072009000 为了求得n边形的内角和,请根据下图所示,完成表格。??????1 2 3 4n-21800360054007200(n-2)×1800你找到规律了吗?例2 已知多边形的每一内角为 150°,求这个多边形的边数.解设这个多边形的边数为n,
根据题意,得(n-2)×1800 =1500 n解这个方程,得n= 12 经检验,符合题意答:这个多边形的边数为12.八边形的内角和是 ;例11080o探索多边形的内角和关键是: 把多边形分成几个三角形,再利用三角形的内角和求得。议
一
议你还有其它的分法吗?PPn×180o-360o(n-1)×180o-180o(课本P55:)
(1) 十边形的内角和是 ; 如果十边形的各个内角都相等,那么它的一个内角是 。
(2)已知一个多边形的内角和是2340°,则这个多边形的边数是_______。1440o144o15巩固练习 1、n边形从一个顶点所画对角线的条数是 ;
2、n边形内角和 = ;
3、九边形的内角和是__________
4、已知一个多边形的边数恰好是从一个顶点所画的对角线的条数的2倍,则此多边形的边数为 ;
5、一个多边形的边数增加1,则内角和增加的度数是(?? ? )
A.60°??????? B.90°?????? C.180°?????? D.360° C 课 堂 测 试 6n-3(n-2)× 180°1260° 如图:某居民小区搞绿化,分别在三角 形、四边形、五边形的广场各角修建半径为1米的花坛。小区绿化组长想先求花坛的面积,再根据面积买花苗。探究 今天的收获 3、n边形的内角和等于:(n-2)×180° 2、n边形从一个顶点所画对角线的条数为:n-3?? 4、利用类比归纳、转化的学习方法,可以把多边形问题转化为三角形问题来解决; 5、方程的数学思想在几何中有重要的作用。 1、 由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形。
A组:课本P62:5、6、7 作业:
FB组:
已知一个多边形除了一个内角外,其余各内角的和是2750°,求这个多边形的边数。
C组:
如图:我国的国旗上的五星是正五角星,正五角星中的五边形ABCDE是正五边形,你能求出五角星中∠F的度数? 祝同学们今后在数学广阔的天空中更加自由的翱翔!再见!
由这图形你能抽象出什么几何图形?你猜到了吗?比
一
比? 1、你能说一说什么叫三角形? 2、你能说出什么叫四边形、五边形、多边形吗? 由 条不在同一直线上的线段首尾顺次连结组成的平面图形,称为 边形。
五四四五nn又称为多边形。 你能说一说下面所指的是多边形的什么? 猜一猜边内角顶点1、什么叫正三角形?什么叫正方形? 3、如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形 (regular polygon)2、什么叫正多边形?归纳: 我们现在研究的是如图8.3.1所示的多边形,是凸多边形; 如图8.3.2所示的多边形,是凹多边形,但不在现在研究的范围中。今后如果不说明,我们讲的多边形都是凸多边形。图 8.3.2比
一
比画出连结下面四点的所有线段: 连结多边形不相邻的两个顶点的线段叫做多边形的对角线。 做
一
做ABCD 你知道三角形、四边形、五边形、六边形等n边形从一个顶点所画的对角线的条数吗?在练习卷上试画一画,并填下表:??????0123n-3探索课后试一试 :你能求n边形的对角线的条数 ? 请同学们利用数学工具,先把你们手上的多边形的内角和计算出来,并完成下表.试一试议一议总结最佳方法: 通过分割成三角形,转
化为利用三角形内角和求出。 1800 3600 540072009000 为了求得n边形的内角和,请根据下图所示,完成表格。??????1 2 3 4n-21800360054007200(n-2)×1800你找到规律了吗?例2 已知多边形的每一内角为 150°,求这个多边形的边数.解设这个多边形的边数为n,
根据题意,得(n-2)×1800 =1500 n解这个方程,得n= 12 经检验,符合题意答:这个多边形的边数为12.八边形的内角和是 ;例11080o探索多边形的内角和关键是: 把多边形分成几个三角形,再利用三角形的内角和求得。议
一
议你还有其它的分法吗?PPn×180o-360o(n-1)×180o-180o(课本P55:)
(1) 十边形的内角和是 ; 如果十边形的各个内角都相等,那么它的一个内角是 。
(2)已知一个多边形的内角和是2340°,则这个多边形的边数是_______。1440o144o15巩固练习 1、n边形从一个顶点所画对角线的条数是 ;
2、n边形内角和 = ;
3、九边形的内角和是__________
4、已知一个多边形的边数恰好是从一个顶点所画的对角线的条数的2倍,则此多边形的边数为 ;
5、一个多边形的边数增加1,则内角和增加的度数是(?? ? )
A.60°??????? B.90°?????? C.180°?????? D.360° C 课 堂 测 试 6n-3(n-2)× 180°1260° 如图:某居民小区搞绿化,分别在三角 形、四边形、五边形的广场各角修建半径为1米的花坛。小区绿化组长想先求花坛的面积,再根据面积买花苗。探究 今天的收获 3、n边形的内角和等于:(n-2)×180° 2、n边形从一个顶点所画对角线的条数为:n-3?? 4、利用类比归纳、转化的学习方法,可以把多边形问题转化为三角形问题来解决; 5、方程的数学思想在几何中有重要的作用。 1、 由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形。
A组:课本P62:5、6、7 作业:
FB组:
已知一个多边形除了一个内角外,其余各内角的和是2750°,求这个多边形的边数。
C组:
如图:我国的国旗上的五星是正五角星,正五角星中的五边形ABCDE是正五边形,你能求出五角星中∠F的度数? 祝同学们今后在数学广阔的天空中更加自由的翱翔!再见!
