江苏省盐城市亭湖区盐城景山中学2023-2024学年八年级上学期10月月考数学试题(含答案)
文档属性
| 名称 | 江苏省盐城市亭湖区盐城景山中学2023-2024学年八年级上学期10月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 440.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 08:47:44 | ||
图片预览



文档简介
2023年秋学期八年级第一次课堂检测
数学试卷
考试时间:100分钟 卷面总分:120分 命题人:倪娜 审核人:严根翔
一.选择题(共8小题,每小题3分,共24分)
1.杭州亚运会将于2023年9月23日举行,下面是杭州亚运会比赛项目中几个项目的图标,其图案可看作轴对称图形的是( )
A.赛艇 B.电子竞技 C.体操 D.柔术
2.16的算术平方根是( )
A.±4 B.4 C.-2 D.-16
3.下列尺规作图,能判断AD是△ABC边上的中线的是( )
A. B. C. D.
4.如图,△ACB≌△A'CB',∠BCB'=30°,则∠ACA'的度数为( )
第4题图
A.25° B.30° C.35° D.40°
5.如图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线.此仪器的原理是( )
第5题图
A.SSS B.SAS C.ASA D.AAS
6.△ABC的三条边分别为a,b,c,下列条件不能判断△ABC是直角三角形的是( )
A.b2=(a+c)(a-c) B.∠A=∠B+∠C
C.∠A:∠B:∠C=3:4:5 D.a=6,b=8,c=10
7.如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED'=50°,则∠EFC等于( )
第7题图
A.65° B.110° C.115° D.130°
8.如图,△ABC中,点D为BC上一点,且AB=AC=CD,则图中∠1和∠2的关系是( )
第8题图
A.∠2=2∠1 B.∠1+2∠2=90° C.2∠1+3∠2=180° D.3∠1+2∠2=180°
二.填空题(共10小题,每小题3分,共30分)
9.如图,一块三角形玻璃板破裂成①,②,③三块,现需要买另一块同样大小的一块三角形玻璃,为了方便,只需带第______块碎片比较好.
第9题图
10.等腰三角形的底角是80°,则它的顶角是______.
11.如图,△ABC≌△DEF,BE=5,BF=1,则CF=______.
第11题图
12.如图是由9个小等边三角形构成的图形,其中已有两个被涂黑,若再涂黑一个,则整个被涂黑的图案构成轴对称图形的方法有______种.
第12题图
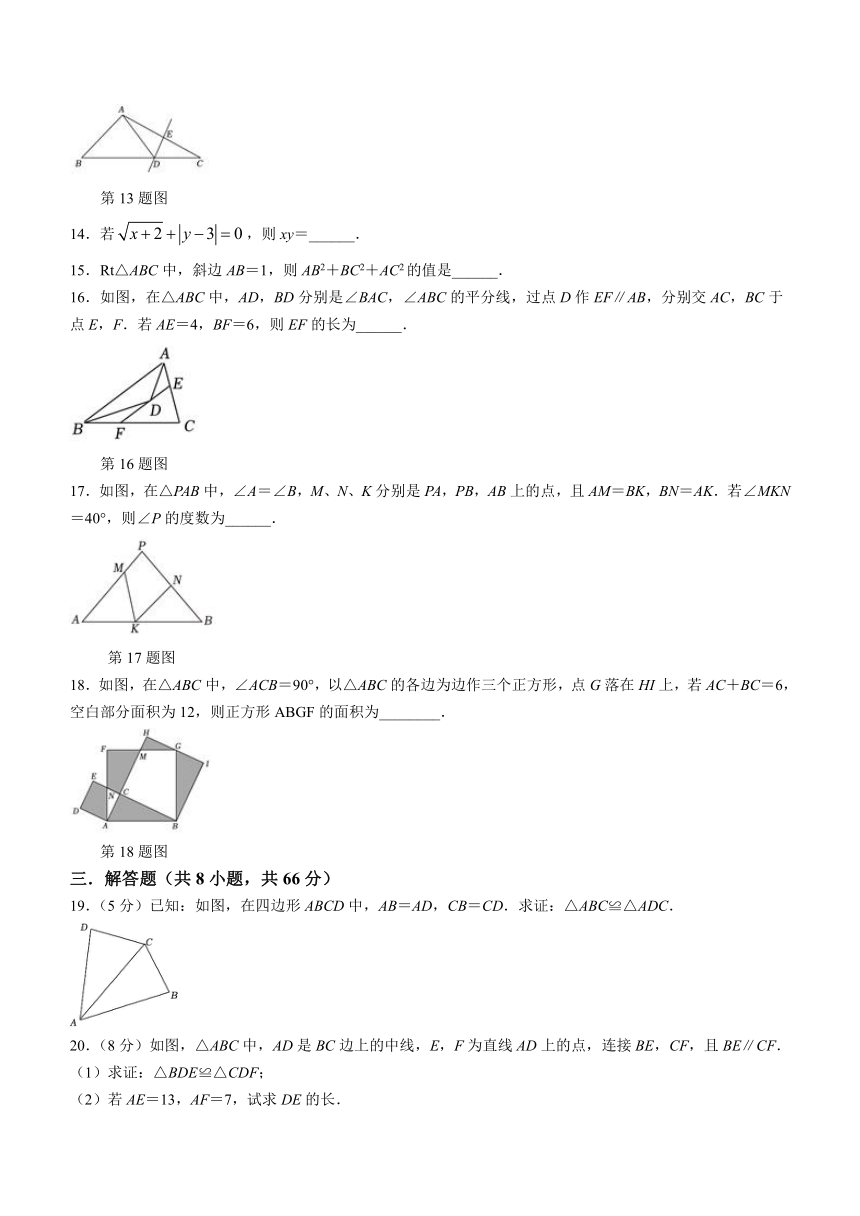
13.如图,在△ABC中,DE是AC的垂直平分线,AB=4,BC=7,则△ABD的周长为______.
第13题图
14.若,则xy=______.
15.Rt△ABC中,斜边AB=1,则AB2+BC2+AC2的值是______.
16.如图,在△ABC中,AD,BD分别是∠BAC,∠ABC的平分线,过点D作EF∥AB,分别交AC,BC于点E,F.若AE=4,BF=6,则EF的长为______.
第16题图
17.如图,在△PAB中,∠A=∠B,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为______.
第17题图
18.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为12,则正方形ABGF的面积为________.
第18题图
三.解答题(共8小题,共66分)
19.(5分)已知:如图,在四边形ABCD中,AB=AD,CB=CD.求证:△ABC≌△ADC.
20.(8分)如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF.
(1)求证:△BDE≌△CDF;
(2)若AE=13,AF=7,试求DE的长.
21.(8分)已知一个正数m的平方根为2n+1和4-3n.
(1)求m的值;
(2),a+b+c的平方根是多少?
22.(8分)在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,
测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.
23.(共9分,每小题3分)如图,在8×6的网格中,每个小正方形的边长均为一个单位.
(1)在图1中画出以BC为一边,面积为12的等腰三角形;
(2)在图2中画出平分△ABC面积的线段BD;
(3)在图3中画出△ABC的角平分线BE.
(请按要求完成下列作图:①仅用无刻度的直尺;②保留作图痕迹;③标注相关字母.)
24.(9分)如图,直角三角形ACB,直角顶点C在直线l上,分别过点A、B作直线l的垂线,垂足分别为点D和点E.
(1)求证:∠DAC=∠BCE;
(2)如果AC=BC.
①求证:CD=BE;
②若设△ADC的三边分别为a、b、c,试用此图证明勾股定理.
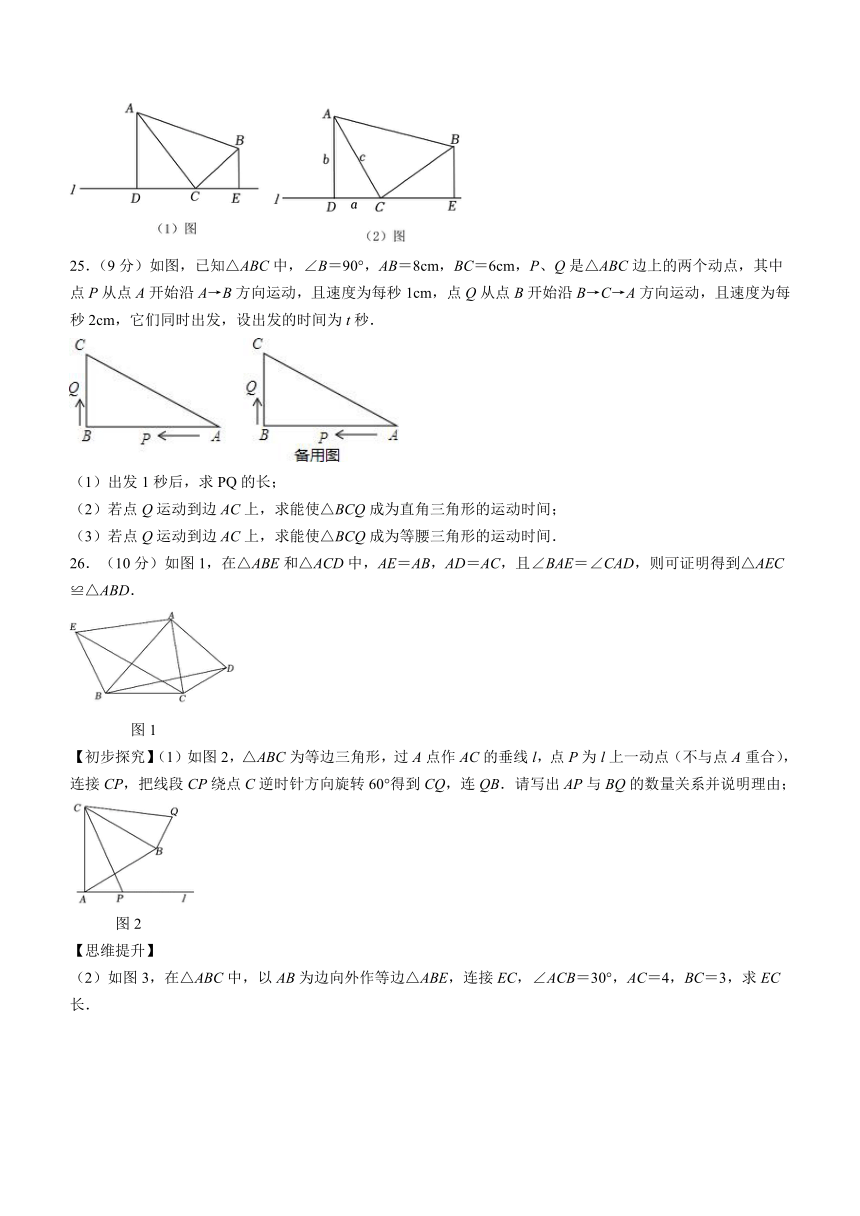
25.(9分)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发1秒后,求PQ的长;
(2)若点Q运动到边AC上,求能使△BCQ成为直角三角形的运动时间;
(3)若点Q运动到边AC上,求能使△BCQ成为等腰三角形的运动时间.
(10分)如图1,在△ABE和△ACD中,AE=AB,AD=AC,且∠BAE=∠CAD,则可证明得到△AEC≌△ABD.
图1
【初步探究】(1)如图2,△ABC为等边三角形,过A点作AC的垂线l,点P为l上一动点(不与点A重合),连接CP,把线段CP绕点C逆时针方向旋转60°得到CQ,连QB.请写出AP与BQ的数量关系并说明理由;
图2
【思维提升】
如图3,在△ABC中,以AB为边向外作等边△ABE,连接EC,∠ACB=30°,AC=4,BC=3,求EC长.
图3
【拓展应用】
(3)如图4,在△ABC中,∠ABC=60°,AB=4,作AD⊥BC交BC于点D,过点B作直线l⊥BC,点H是直线l上的一个动点,线段AH绕点A按顺时针方向旋转30°得到线段AH′,则AH'+BH'的最小值为_______.
图4
景山2023年秋学期八年级第一次课堂检测
数学参考答案
一、选择题:
1.B 2.B 3.A 4.B 5.A 6.C 7.C 8.C
二、填空题:
9.③ 10.20° 11.3 12.3 13.11
14.-6 15.2 16.10 17.100° 18.20
三、解答题:
19.证明:在△ABC和△ADC中,,
∴△ABC≌△ADC(SSS).
20.(1)证明:∵AD是BC边上的中线,∴BD=CD,
∵BE∥CF,∴∠DBE=∠DCF,
在△BDE和△CDF中,
∴△BDE≌△CDF(ASA);
(2)解:∵AE=13,AF=7,∴EF=AE-AF=13-7=6,
∵△BDE≌△CDF,∴DE=DF,
∵DE+DF=EF=6,
∴DE=3.
21.(1)∵正数m的平方根为2n+1和4-3n,正数m的平方根互为相反数,
∴2n+1+4-3n=0,∴n=5,∴2n+1=11,
∴m=121;
(2)∵,
∴a-1=0,b=0,c-n=0,∴a=1,b=0,c=n=5,
∴a+b+c=1+0+5=6,
∴a+b+c的平方根是.
22.解:(1)是,
理由是:在△CHB中,
∵,
∴
∴CH⊥AB,
所以CH是从村庄C到河边的最近路
(2)设AC=x
在Rt△ACH中,由已知得AC=x,AH=x-1.8,CH=2.4
由勾股定理得:
∴
解这个方程,得x=2.5,
答:原来的路线AC的长为2.5千米.
23.(每个图3分)
解:(1)△ABC即为所求;(2)线段DB即为所求;
(3)BE为△ABC的角平分线BE.
24.证明:(1)∵∠ACB=90°,AD⊥DE于点D,
∴∠DAC+∠ACD=90°,∠ADC+∠BCE=90°,
∴∠DAC=∠BCE;
(2)①∵AD⊥DE于点D,BE⊥DE于点E,
∴∠ADC=∠CEB=90°,
由(1)知:∠DAC=∠BCE,
在△ADC和△CEB中,,
∴△ADC≌△CEB(AAS),
∴CD=BE;
②由图可知:
,
∴,
化简,得:.
25.解:(1)当t=1时,AP=1cm,BQ=2cm,
∴BP=7cm,∴,
∴;
(2)当∠BQC=90°时,
∵∠ABC=90°,由勾股定理得,AC=10cm,
∴(cm),
在Rt△BCQ中,由勾股定理得,(cm),
∴t=(BC+CQ)÷2=4.8,
当∠CBQ=90°时,点Q与A重合,
∴t=(BC+AC)÷2=8,
综上所述:t=4.8或8;
(3)当点Q在AC上时,AQ=BC+AC-2t=16-2t,
∴CQ=AC-AQ=10-(16-2t)=2t-6,
∵△BCQ为等腰三角形,
∴有BQ=BC,CQ=BC和CQ=BQ三种情况,
①当BQ=BC=6时,如图1,过B作BD⊥AC于D,
则.
在Rt△ABC中,,
∴,
在Rt△BCD中,由勾股定理可得,
即,解得或(舍去);
②当CQ=BC=6时,则2t-6=6,解得t=6;
③当CQ=BQ时,则∠C=∠QBC,
∴∠C+∠A=∠CBQ+∠QBA,∴∠A=∠QBA,∴QB=QA,
∴,即2t-6=5,解得t=5.5;
26.解:(1)AP=BQ,理由如下:
在等边△ABC中,AC=BC,∠ACB=60°,
由旋转可得,CP=CQ,∠PCQ=60°,∴∠ACB=∠PCQ,
∴∠ACB-∠PCB=∠PCQ-∠PCB,即∠ACP=∠BCQ,
∴△ACP≌△BCQ(SAS),∴AP=BQ;
(2)如图1,
作等边三角形ACD,连接BD,
∴∠ACD=60°,CD=AC=4,
∵∠ACB=30°,∴∠BCD=90°,
∴;
(3)()
数学试卷
考试时间:100分钟 卷面总分:120分 命题人:倪娜 审核人:严根翔
一.选择题(共8小题,每小题3分,共24分)
1.杭州亚运会将于2023年9月23日举行,下面是杭州亚运会比赛项目中几个项目的图标,其图案可看作轴对称图形的是( )
A.赛艇 B.电子竞技 C.体操 D.柔术
2.16的算术平方根是( )
A.±4 B.4 C.-2 D.-16
3.下列尺规作图,能判断AD是△ABC边上的中线的是( )
A. B. C. D.
4.如图,△ACB≌△A'CB',∠BCB'=30°,则∠ACA'的度数为( )
第4题图
A.25° B.30° C.35° D.40°
5.如图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线.此仪器的原理是( )
第5题图
A.SSS B.SAS C.ASA D.AAS
6.△ABC的三条边分别为a,b,c,下列条件不能判断△ABC是直角三角形的是( )
A.b2=(a+c)(a-c) B.∠A=∠B+∠C
C.∠A:∠B:∠C=3:4:5 D.a=6,b=8,c=10
7.如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED'=50°,则∠EFC等于( )
第7题图
A.65° B.110° C.115° D.130°
8.如图,△ABC中,点D为BC上一点,且AB=AC=CD,则图中∠1和∠2的关系是( )
第8题图
A.∠2=2∠1 B.∠1+2∠2=90° C.2∠1+3∠2=180° D.3∠1+2∠2=180°
二.填空题(共10小题,每小题3分,共30分)
9.如图,一块三角形玻璃板破裂成①,②,③三块,现需要买另一块同样大小的一块三角形玻璃,为了方便,只需带第______块碎片比较好.
第9题图
10.等腰三角形的底角是80°,则它的顶角是______.
11.如图,△ABC≌△DEF,BE=5,BF=1,则CF=______.
第11题图
12.如图是由9个小等边三角形构成的图形,其中已有两个被涂黑,若再涂黑一个,则整个被涂黑的图案构成轴对称图形的方法有______种.
第12题图
13.如图,在△ABC中,DE是AC的垂直平分线,AB=4,BC=7,则△ABD的周长为______.
第13题图
14.若,则xy=______.
15.Rt△ABC中,斜边AB=1,则AB2+BC2+AC2的值是______.
16.如图,在△ABC中,AD,BD分别是∠BAC,∠ABC的平分线,过点D作EF∥AB,分别交AC,BC于点E,F.若AE=4,BF=6,则EF的长为______.
第16题图
17.如图,在△PAB中,∠A=∠B,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为______.
第17题图
18.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为12,则正方形ABGF的面积为________.
第18题图
三.解答题(共8小题,共66分)
19.(5分)已知:如图,在四边形ABCD中,AB=AD,CB=CD.求证:△ABC≌△ADC.
20.(8分)如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF.
(1)求证:△BDE≌△CDF;
(2)若AE=13,AF=7,试求DE的长.
21.(8分)已知一个正数m的平方根为2n+1和4-3n.
(1)求m的值;
(2),a+b+c的平方根是多少?
22.(8分)在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,
测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.
23.(共9分,每小题3分)如图,在8×6的网格中,每个小正方形的边长均为一个单位.
(1)在图1中画出以BC为一边,面积为12的等腰三角形;
(2)在图2中画出平分△ABC面积的线段BD;
(3)在图3中画出△ABC的角平分线BE.
(请按要求完成下列作图:①仅用无刻度的直尺;②保留作图痕迹;③标注相关字母.)
24.(9分)如图,直角三角形ACB,直角顶点C在直线l上,分别过点A、B作直线l的垂线,垂足分别为点D和点E.
(1)求证:∠DAC=∠BCE;
(2)如果AC=BC.
①求证:CD=BE;
②若设△ADC的三边分别为a、b、c,试用此图证明勾股定理.
25.(9分)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发1秒后,求PQ的长;
(2)若点Q运动到边AC上,求能使△BCQ成为直角三角形的运动时间;
(3)若点Q运动到边AC上,求能使△BCQ成为等腰三角形的运动时间.
(10分)如图1,在△ABE和△ACD中,AE=AB,AD=AC,且∠BAE=∠CAD,则可证明得到△AEC≌△ABD.
图1
【初步探究】(1)如图2,△ABC为等边三角形,过A点作AC的垂线l,点P为l上一动点(不与点A重合),连接CP,把线段CP绕点C逆时针方向旋转60°得到CQ,连QB.请写出AP与BQ的数量关系并说明理由;
图2
【思维提升】
如图3,在△ABC中,以AB为边向外作等边△ABE,连接EC,∠ACB=30°,AC=4,BC=3,求EC长.
图3
【拓展应用】
(3)如图4,在△ABC中,∠ABC=60°,AB=4,作AD⊥BC交BC于点D,过点B作直线l⊥BC,点H是直线l上的一个动点,线段AH绕点A按顺时针方向旋转30°得到线段AH′,则AH'+BH'的最小值为_______.
图4
景山2023年秋学期八年级第一次课堂检测
数学参考答案
一、选择题:
1.B 2.B 3.A 4.B 5.A 6.C 7.C 8.C
二、填空题:
9.③ 10.20° 11.3 12.3 13.11
14.-6 15.2 16.10 17.100° 18.20
三、解答题:
19.证明:在△ABC和△ADC中,,
∴△ABC≌△ADC(SSS).
20.(1)证明:∵AD是BC边上的中线,∴BD=CD,
∵BE∥CF,∴∠DBE=∠DCF,
在△BDE和△CDF中,
∴△BDE≌△CDF(ASA);
(2)解:∵AE=13,AF=7,∴EF=AE-AF=13-7=6,
∵△BDE≌△CDF,∴DE=DF,
∵DE+DF=EF=6,
∴DE=3.
21.(1)∵正数m的平方根为2n+1和4-3n,正数m的平方根互为相反数,
∴2n+1+4-3n=0,∴n=5,∴2n+1=11,
∴m=121;
(2)∵,
∴a-1=0,b=0,c-n=0,∴a=1,b=0,c=n=5,
∴a+b+c=1+0+5=6,
∴a+b+c的平方根是.
22.解:(1)是,
理由是:在△CHB中,
∵,
∴
∴CH⊥AB,
所以CH是从村庄C到河边的最近路
(2)设AC=x
在Rt△ACH中,由已知得AC=x,AH=x-1.8,CH=2.4
由勾股定理得:
∴
解这个方程,得x=2.5,
答:原来的路线AC的长为2.5千米.
23.(每个图3分)
解:(1)△ABC即为所求;(2)线段DB即为所求;
(3)BE为△ABC的角平分线BE.
24.证明:(1)∵∠ACB=90°,AD⊥DE于点D,
∴∠DAC+∠ACD=90°,∠ADC+∠BCE=90°,
∴∠DAC=∠BCE;
(2)①∵AD⊥DE于点D,BE⊥DE于点E,
∴∠ADC=∠CEB=90°,
由(1)知:∠DAC=∠BCE,
在△ADC和△CEB中,,
∴△ADC≌△CEB(AAS),
∴CD=BE;
②由图可知:
,
∴,
化简,得:.
25.解:(1)当t=1时,AP=1cm,BQ=2cm,
∴BP=7cm,∴,
∴;
(2)当∠BQC=90°时,
∵∠ABC=90°,由勾股定理得,AC=10cm,
∴(cm),
在Rt△BCQ中,由勾股定理得,(cm),
∴t=(BC+CQ)÷2=4.8,
当∠CBQ=90°时,点Q与A重合,
∴t=(BC+AC)÷2=8,
综上所述:t=4.8或8;
(3)当点Q在AC上时,AQ=BC+AC-2t=16-2t,
∴CQ=AC-AQ=10-(16-2t)=2t-6,
∵△BCQ为等腰三角形,
∴有BQ=BC,CQ=BC和CQ=BQ三种情况,
①当BQ=BC=6时,如图1,过B作BD⊥AC于D,
则.
在Rt△ABC中,,
∴,
在Rt△BCD中,由勾股定理可得,
即,解得或(舍去);
②当CQ=BC=6时,则2t-6=6,解得t=6;
③当CQ=BQ时,则∠C=∠QBC,
∴∠C+∠A=∠CBQ+∠QBA,∴∠A=∠QBA,∴QB=QA,
∴,即2t-6=5,解得t=5.5;
26.解:(1)AP=BQ,理由如下:
在等边△ABC中,AC=BC,∠ACB=60°,
由旋转可得,CP=CQ,∠PCQ=60°,∴∠ACB=∠PCQ,
∴∠ACB-∠PCB=∠PCQ-∠PCB,即∠ACP=∠BCQ,
∴△ACP≌△BCQ(SAS),∴AP=BQ;
(2)如图1,
作等边三角形ACD,连接BD,
∴∠ACD=60°,CD=AC=4,
∵∠ACB=30°,∴∠BCD=90°,
∴;
(3)()
同课章节目录
