2023-2024学年甘肃省武威市凉州区人教版八年级第一学期数学第十一章 三角形 单元测试题(含答案)
文档属性
| 名称 | 2023-2024学年甘肃省武威市凉州区人教版八年级第一学期数学第十一章 三角形 单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 172.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 08:47:58 | ||
图片预览


文档简介
2023-2024学年甘肃省武威市凉州区八年级第一学期数学第十一章 三角形单元测试题人教版
一、选择题(每小题3分,共30分)
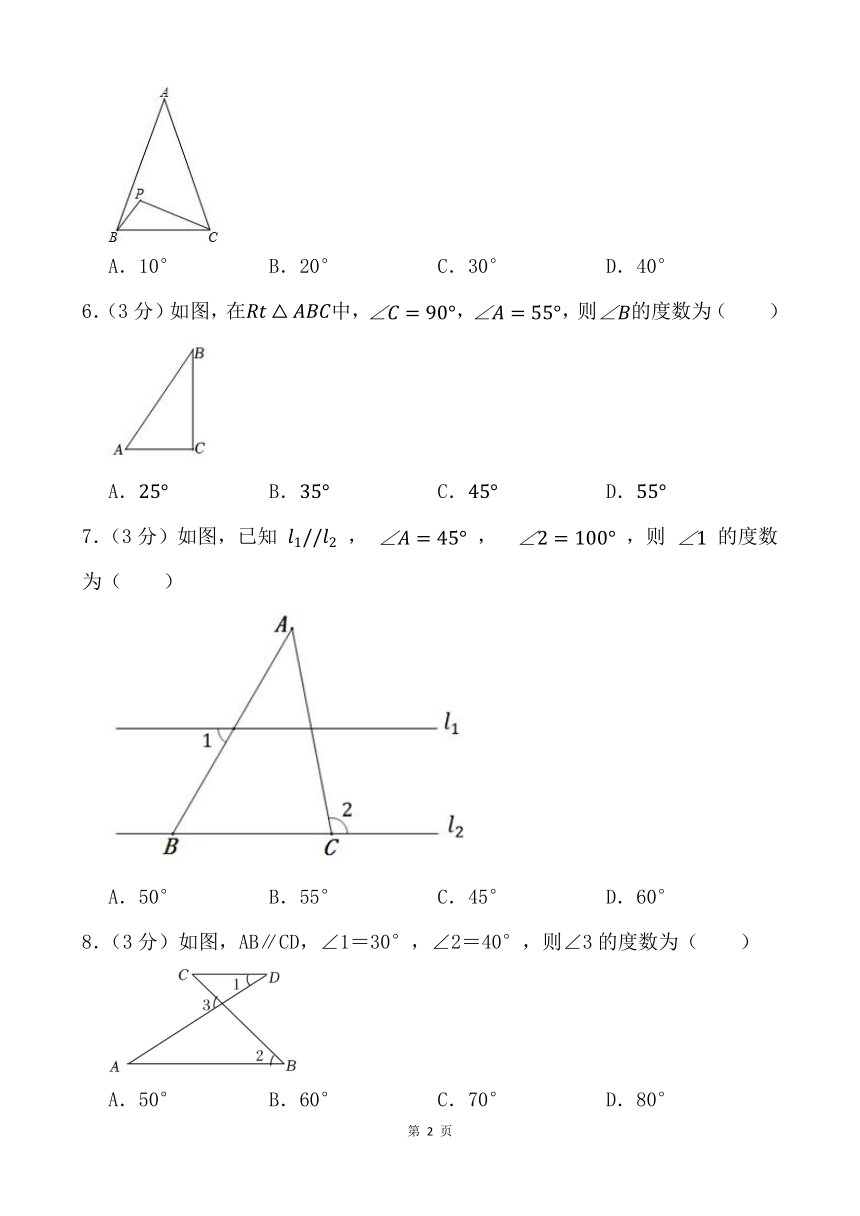
1.(3分)下列长度的三条线段能组成三角形的是( )
A. B. C. D.
2.(3分)如图,BD是△ABC的中线,点E为BD上一点,BE=2ED,连接AE并延长,交BC于点F,若△ABC的面积是24cm2,则△AED的面积是( )
A.2cm2 B.3cm2 C.4cm2 D.6cm2
3.(3分)如图,在△ABC中,AB=12,BC=13,AC=5,则BC边上的高AD为( )
A.3 B.4 C. D.4.8
4.(3分)生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的( )
A.全等形 B.稳定性 C.灵活性 D.对称性
5.(3分)如图,在中,,P为内的一点,且,,则∠A的大小为( )
A.10° B.20° C.30° D.40°
6.(3分)如图,在中,,,则的度数为( )
A. B. C. D.
7.(3分)如图,已知 , , ,则 的度数为( )
A.50° B.55° C.45° D.60°
8.(3分)如图,AB∥CD,∠1=30°,∠2=40°,则∠3的度数为( )
A.50° B.60° C.70° D.80°
9.(3分)多边形的每一个外角都是,则此多边形从一个顶点出发的对角线有( )条.
A.7条 B.8条 C.9条 D.10条
10.(3分)如图,在△ABC中,∠C=70°,沿图中虚线截去∠C,则∠1+∠2=( )
A.360° B.250° C.180° D.140°
二、填空题(每小题3分,共30分)
11.(3分)已知的三边长分别是、、,化简 .
12.(3分)已知三角形的三边长分别是8、10、x,则x的取值范围是 .
13.(3分)如图,已知,分别是的中线和高,若,,则的面积是 .
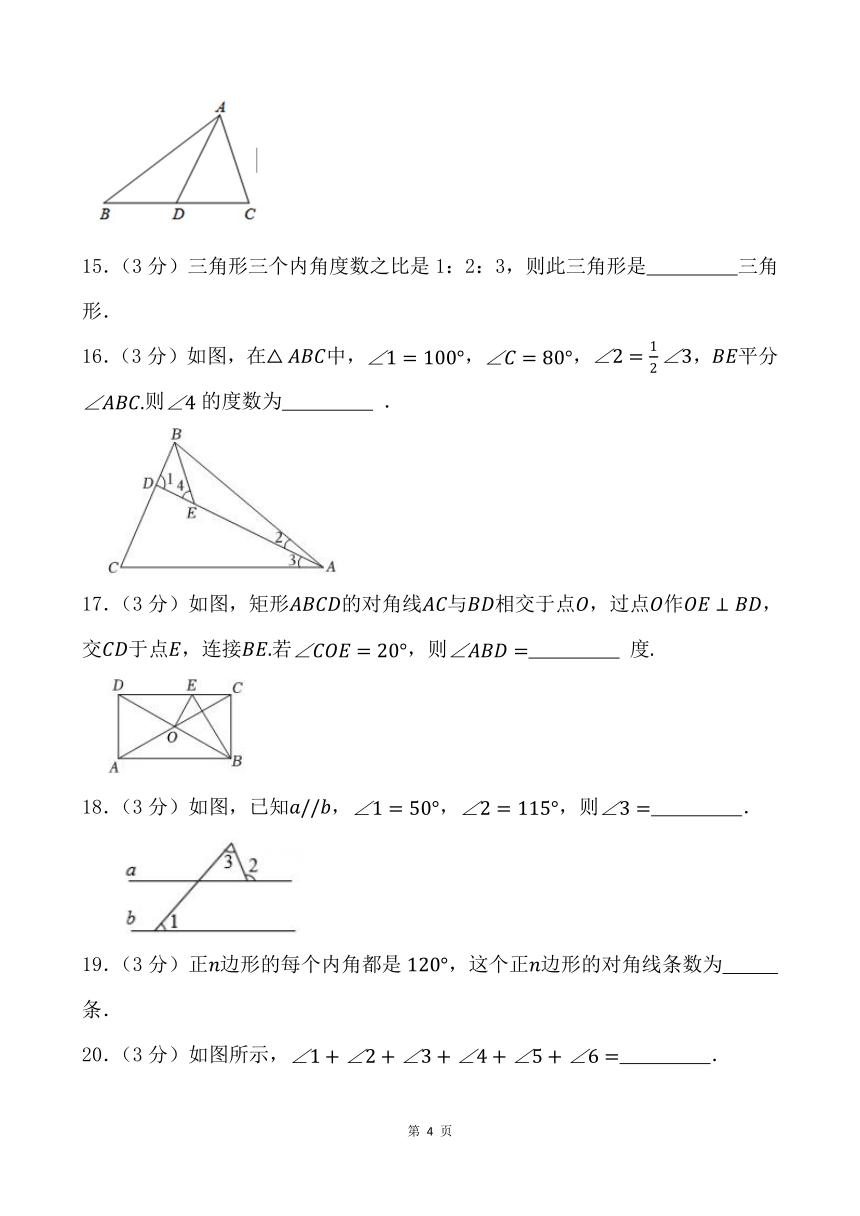
14.(3分) 如图,是的一条中线,若,则 .
15.(3分)三角形三个内角度数之比是1:2:3,则此三角形是 三角形.
16.(3分)如图,在中,,,,平分则的度数为 .
17.(3分)如图,矩形的对角线与相交于点,过点作,交于点,连接若,则 度
18.(3分)如图,已知,,,则 .
19.(3分)正边形的每个内角都是,这个正边形的对角线条数为 条.
20.(3分)如图所示, .
三、作图题(保留作图痕迹,不必写作法)(共4分)
21.如图,已知△ABC中,AB=2AC,作一条射线AD交线段BC于点D,使△ABD的面积是△ACD的面积的2倍.
四、解答题(共56分)
22.(6分)已知一个多边形的内角和是外角和的4倍,求边数.
23.(6分)一个等腰三角形的一个内角比另一个内角的2倍少30°,求这个三角形的顶角的度数.
24.(8分)如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
25.(8分)已知:如图,四边形ABCD中,AB⊥BC,AB=2,BC=3,CD=6,AD=7,求四边形ABCD的面积.
26.(8分)如图,已知AE⊥BC,AD平分∠BAE,∠ADB=110°,∠CAE=20°,求∠BAC和∠B的度数.
27.(10分)如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.
(1)(5分)求证:BC=DC;
(2)(5分)若∠A=25°,∠D=15°,求∠ACB的度数.
28.(10分)已知:如图,在 中,是边上的高线,是边上 的中线,G是的中点,连结,,,.
(1)(5分)求的长.
(2)(5分)求证:.
答案
1.B 2.C 3.C 4.B 5.B 6.B 7.B 8.C 9.C 10.B
11. 12.2<x<18 13.12 14.10 15.直角 16.45° 17.35
18. 19.9 20.
21.解:如图:
22.边数为10.
23.①30°,30°,120°
②48°,66°,66°;
③这个三角形的顶角为120°或48°或75°.
24.∠DAC=20°.
25..
26.∠B=50° ∠BAC=60°.
27.(1)解:∵ ∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ACE,
∴∠BCA=∠DCE,
∵ EC=AC,∠A=∠E,
∴ BCA≌ DCE(ASA),
∴BC=DC;
(2)∠ACB=140°.
28.(1)
(2)证明:连接,
∵,是边上 的中线,
∴ ,
∴,
∵G是的中点,
∴.
一、选择题(每小题3分,共30分)
1.(3分)下列长度的三条线段能组成三角形的是( )
A. B. C. D.
2.(3分)如图,BD是△ABC的中线,点E为BD上一点,BE=2ED,连接AE并延长,交BC于点F,若△ABC的面积是24cm2,则△AED的面积是( )
A.2cm2 B.3cm2 C.4cm2 D.6cm2
3.(3分)如图,在△ABC中,AB=12,BC=13,AC=5,则BC边上的高AD为( )
A.3 B.4 C. D.4.8
4.(3分)生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的( )
A.全等形 B.稳定性 C.灵活性 D.对称性
5.(3分)如图,在中,,P为内的一点,且,,则∠A的大小为( )
A.10° B.20° C.30° D.40°
6.(3分)如图,在中,,,则的度数为( )
A. B. C. D.
7.(3分)如图,已知 , , ,则 的度数为( )
A.50° B.55° C.45° D.60°
8.(3分)如图,AB∥CD,∠1=30°,∠2=40°,则∠3的度数为( )
A.50° B.60° C.70° D.80°
9.(3分)多边形的每一个外角都是,则此多边形从一个顶点出发的对角线有( )条.
A.7条 B.8条 C.9条 D.10条
10.(3分)如图,在△ABC中,∠C=70°,沿图中虚线截去∠C,则∠1+∠2=( )
A.360° B.250° C.180° D.140°
二、填空题(每小题3分,共30分)
11.(3分)已知的三边长分别是、、,化简 .
12.(3分)已知三角形的三边长分别是8、10、x,则x的取值范围是 .
13.(3分)如图,已知,分别是的中线和高,若,,则的面积是 .
14.(3分) 如图,是的一条中线,若,则 .
15.(3分)三角形三个内角度数之比是1:2:3,则此三角形是 三角形.
16.(3分)如图,在中,,,,平分则的度数为 .
17.(3分)如图,矩形的对角线与相交于点,过点作,交于点,连接若,则 度
18.(3分)如图,已知,,,则 .
19.(3分)正边形的每个内角都是,这个正边形的对角线条数为 条.
20.(3分)如图所示, .
三、作图题(保留作图痕迹,不必写作法)(共4分)
21.如图,已知△ABC中,AB=2AC,作一条射线AD交线段BC于点D,使△ABD的面积是△ACD的面积的2倍.
四、解答题(共56分)
22.(6分)已知一个多边形的内角和是外角和的4倍,求边数.
23.(6分)一个等腰三角形的一个内角比另一个内角的2倍少30°,求这个三角形的顶角的度数.
24.(8分)如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
25.(8分)已知:如图,四边形ABCD中,AB⊥BC,AB=2,BC=3,CD=6,AD=7,求四边形ABCD的面积.
26.(8分)如图,已知AE⊥BC,AD平分∠BAE,∠ADB=110°,∠CAE=20°,求∠BAC和∠B的度数.
27.(10分)如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.
(1)(5分)求证:BC=DC;
(2)(5分)若∠A=25°,∠D=15°,求∠ACB的度数.
28.(10分)已知:如图,在 中,是边上的高线,是边上 的中线,G是的中点,连结,,,.
(1)(5分)求的长.
(2)(5分)求证:.
答案
1.B 2.C 3.C 4.B 5.B 6.B 7.B 8.C 9.C 10.B
11. 12.2<x<18 13.12 14.10 15.直角 16.45° 17.35
18. 19.9 20.
21.解:如图:
22.边数为10.
23.①30°,30°,120°
②48°,66°,66°;
③这个三角形的顶角为120°或48°或75°.
24.∠DAC=20°.
25..
26.∠B=50° ∠BAC=60°.
27.(1)解:∵ ∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ACE,
∴∠BCA=∠DCE,
∵ EC=AC,∠A=∠E,
∴ BCA≌ DCE(ASA),
∴BC=DC;
(2)∠ACB=140°.
28.(1)
(2)证明:连接,
∵,是边上 的中线,
∴ ,
∴,
∵G是的中点,
∴.
