18.2正比例函数的图像(第2课时)教学课件(共27张PPT) 2023-2024学年八年级数学上册(沪教版)
文档属性
| 名称 | 18.2正比例函数的图像(第2课时)教学课件(共27张PPT) 2023-2024学年八年级数学上册(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 22:29:03 | ||
图片预览






文档简介
(共27张PPT)
沪教版八年级上册
第18章 正比例函数与反比例函数
18.2正比例函数的图像(第2课时)
学习目标
1.了解画函数图像的一般步骤. (重点)
2.了解正比例函数的图像和性质并会画正比例函数图像. (重点)
1、下列函数中哪些是正比例函数?
(1)y =2x
(2)y=x2+1
(3)
(4)
是
是
不是
不是
看变量之间是否
满足函数的定义:
即形如 y=kx
(k是常数,k≠0)
知识回顾
1、若 y =5x 3m-2 是正比例函数,
则 m = 。
2、若 是正比例函数,
则 m = 。
注意:
1、使自变量的指数为1
2、系数不为0
3、常数项为零
3、
若
是正比例函数,
则 k = ( ),
此时的函数解析式为
( )
1
-2
-2
y=-4x
知识回顾
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
-4
-2
0
2
4
y=2x
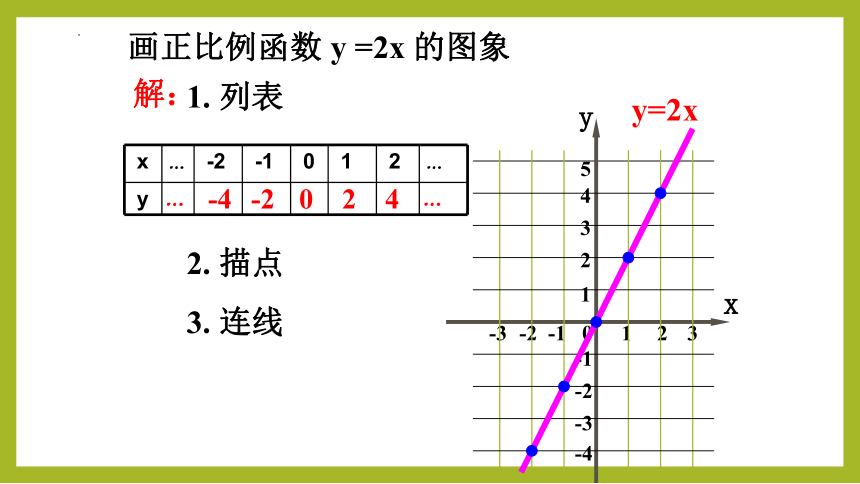
x … -2 -1 0 1 2 …
y
画正比例函数 y =2x 的图象
解:
1. 列表
2. 描点
3. 连线
…
…
6
4
2
0
-2
-4
-6
x
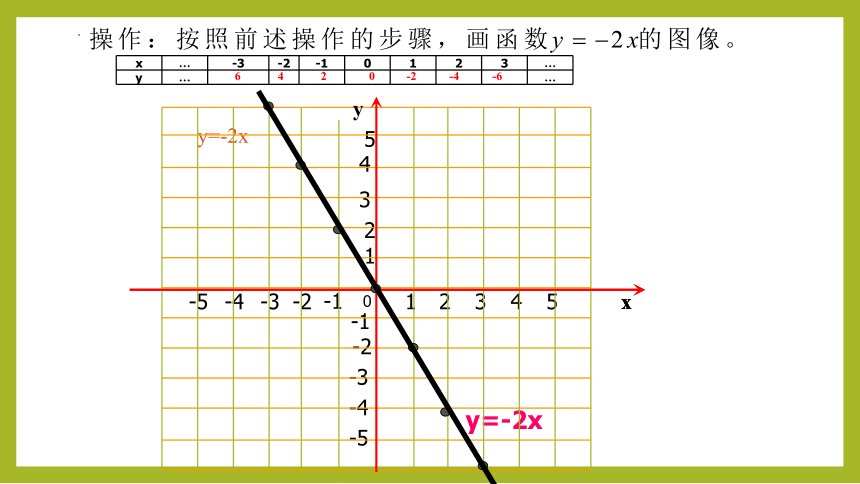
y=-2x
x … -3 -2 -1 0 1 2 3 …
y … …
x
-5
-4
-3
y=-2x
-2
-1
5
4
3
2
1
-1
-2
-3
-4
-5
1
2
3
4
5
x
y
0
-1
5
4
3
2
1
-2
-3
-4
-5
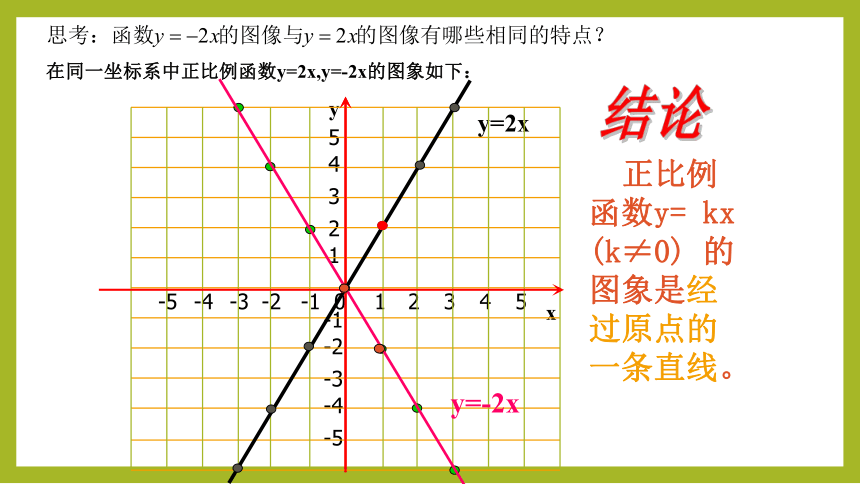
在同一坐标系中正比例函数y=2x,y=-2x的图象如下:
x
-5
-4
-3
-2
-1 0
1
2
3
4
5
y
y=2x
y=-2x
正比例函数y= kx (k≠0) 的图象是经过原点的一条直线。
结论
我有新发现:
正比例函数y= kx (k≠0)
的图象是经过原点(0,0)和(1,k)的一条直线。
y=x
y=3x
1
y
x
o
3
3
1
1
y
x
o
当k>0时,它的图像 经过第一、三象限,y随x的增大而增大
什么时候正比例函数图像经过第一三象限?
3
3
1
y=3x
y=x
1
y
x
o
当k<0时,它的图像经过第二、四像限,y随x的增大而减小
什么时候正比例函数图像经过第二四象限?
y=-3x
y=-x
y=- x
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
x
y
1
y=2x
两点法画出正比例函数 的图象
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
x
y
1
y=2x
对比K的取值,它们的图像都经过哪几个象限?
从左到右呈什么趋势?这说明Y随着X的增大如何变化?
正比例函数y= kx (k≠0) 的图象是
当k>0时,直线y=kx 经过第一、三象限;
当k<0时,直线y=kx 经过第二、四象限。
一条经过原点的直线。
从左向右上升,即随着x的增大y也增大
从左向右下降,即随着x的增大y反而减小
拓展与延伸
当 |k| 越大时,图像越靠近y轴;
当 |k| 相等时,图像关于坐标轴对称。
课本练习
1.正比例函数y=kx的图象如图所示,则k
的取值范围是( )
A.k>0 B.k<0
C.k>1 D.k<1
A
随堂检测
2.若正比例函数的图象经过点(2,-3),则这个图象必经过点( )
A.(-3,-2) B.(2,3)
C.(3,-2) D.(-2,3)
D
3.若正比例函数y=(3k-5)x的图象如图所示,则k的取值范围是________.
4.当k>0时,正比例函数y=kx的图象大致是( )
5.设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m等于( )
A.2 B.-2 C.4 D.-4
A
B
6.已知函数y=3x的图象经过点A(-1,y1)、点 B(-2,y2),则y1________y2.(填“>”“<”或“=”)
分析:
方法一:把点A、点B的坐标分别代入函数
y=3x,求出y1,y2的值比较大小即可.
>
方法二:画出正比例函数y=3x的图象,在函数图象上标出点A、点B,利用数形结合思想来比较y1,y2的大小.如图,观察图形,显然可得y1>y2.
方法三:根据正比例函数的增减性来比较函数值的大小.根据正比例函数的性质,当k>0时,y的值随着x值的增大而增大,即可 得y1>y2.
如何画正比例函数的图像?
画正比例函数的图像时,只需描两个点,然后过这两个点画一条直线
因为正比例函数的图像是一条直线,而两点确定一条直线
课堂小结
沪教版八年级上册
第18章 正比例函数与反比例函数
18.2正比例函数的图像(第2课时)
学习目标
1.了解画函数图像的一般步骤. (重点)
2.了解正比例函数的图像和性质并会画正比例函数图像. (重点)
1、下列函数中哪些是正比例函数?
(1)y =2x
(2)y=x2+1
(3)
(4)
是
是
不是
不是
看变量之间是否
满足函数的定义:
即形如 y=kx
(k是常数,k≠0)
知识回顾
1、若 y =5x 3m-2 是正比例函数,
则 m = 。
2、若 是正比例函数,
则 m = 。
注意:
1、使自变量的指数为1
2、系数不为0
3、常数项为零
3、
若
是正比例函数,
则 k = ( ),
此时的函数解析式为
( )
1
-2
-2
y=-4x
知识回顾
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
-4
-2
0
2
4
y=2x
x … -2 -1 0 1 2 …
y
画正比例函数 y =2x 的图象
解:
1. 列表
2. 描点
3. 连线
…
…
6
4
2
0
-2
-4
-6
x
y=-2x
x … -3 -2 -1 0 1 2 3 …
y … …
x
-5
-4
-3
y=-2x
-2
-1
5
4
3
2
1
-1
-2
-3
-4
-5
1
2
3
4
5
x
y
0
-1
5
4
3
2
1
-2
-3
-4
-5
在同一坐标系中正比例函数y=2x,y=-2x的图象如下:
x
-5
-4
-3
-2
-1 0
1
2
3
4
5
y
y=2x
y=-2x
正比例函数y= kx (k≠0) 的图象是经过原点的一条直线。
结论
我有新发现:
正比例函数y= kx (k≠0)
的图象是经过原点(0,0)和(1,k)的一条直线。
y=x
y=3x
1
y
x
o
3
3
1
1
y
x
o
当k>0时,它的图像 经过第一、三象限,y随x的增大而增大
什么时候正比例函数图像经过第一三象限?
3
3
1
y=3x
y=x
1
y
x
o
当k<0时,它的图像经过第二、四像限,y随x的增大而减小
什么时候正比例函数图像经过第二四象限?
y=-3x
y=-x
y=- x
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
x
y
1
y=2x
两点法画出正比例函数 的图象
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
x
y
1
y=2x
对比K的取值,它们的图像都经过哪几个象限?
从左到右呈什么趋势?这说明Y随着X的增大如何变化?
正比例函数y= kx (k≠0) 的图象是
当k>0时,直线y=kx 经过第一、三象限;
当k<0时,直线y=kx 经过第二、四象限。
一条经过原点的直线。
从左向右上升,即随着x的增大y也增大
从左向右下降,即随着x的增大y反而减小
拓展与延伸
当 |k| 越大时,图像越靠近y轴;
当 |k| 相等时,图像关于坐标轴对称。
课本练习
1.正比例函数y=kx的图象如图所示,则k
的取值范围是( )
A.k>0 B.k<0
C.k>1 D.k<1
A
随堂检测
2.若正比例函数的图象经过点(2,-3),则这个图象必经过点( )
A.(-3,-2) B.(2,3)
C.(3,-2) D.(-2,3)
D
3.若正比例函数y=(3k-5)x的图象如图所示,则k的取值范围是________.
4.当k>0时,正比例函数y=kx的图象大致是( )
5.设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m等于( )
A.2 B.-2 C.4 D.-4
A
B
6.已知函数y=3x的图象经过点A(-1,y1)、点 B(-2,y2),则y1________y2.(填“>”“<”或“=”)
分析:
方法一:把点A、点B的坐标分别代入函数
y=3x,求出y1,y2的值比较大小即可.
>
方法二:画出正比例函数y=3x的图象,在函数图象上标出点A、点B,利用数形结合思想来比较y1,y2的大小.如图,观察图形,显然可得y1>y2.
方法三:根据正比例函数的增减性来比较函数值的大小.根据正比例函数的性质,当k>0时,y的值随着x值的增大而增大,即可 得y1>y2.
如何画正比例函数的图像?
画正比例函数的图像时,只需描两个点,然后过这两个点画一条直线
因为正比例函数的图像是一条直线,而两点确定一条直线
课堂小结
