专题22.30实际问题与二次函数 分层练习基础练(含解析)2023-2024学年九年级数学上册人教版专项讲练
文档属性
| 名称 | 专题22.30实际问题与二次函数 分层练习基础练(含解析)2023-2024学年九年级数学上册人教版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 679.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 00:00:00 | ||
图片预览

文档简介
专题22.30 实际问题与二次函数(分层练习)(基础练)
一、单选题
1.如图,用绳子围成周长为的矩形,记矩形的一边长为,矩形的面积为.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为( )
A. B.
C. D.
2.如图(1)是一个横断面为抛物线形状的拱桥,当水面在时,拱顶(拱桥洞的最高点)离水面2 m,水面宽4 m.如图(2)建立平面直角坐标系,则抛物线的解析式是( )
A. B. C. D.
3.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价每提高2元,则每天少卖4套.设冰墩墩和雪容融套件每套售价定为x元时,则该商品每天销售套件所获利润w与x之间的函数关系式为( ).
A. B.
C. D.
4.小明在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形,若实心球运动的抛物线的表达式为,其中是实心球飞行的高度,是实心球飞行的水平距离,则小明此次郑球过程中,实心球的最大高度是( )
A. B. C. D.
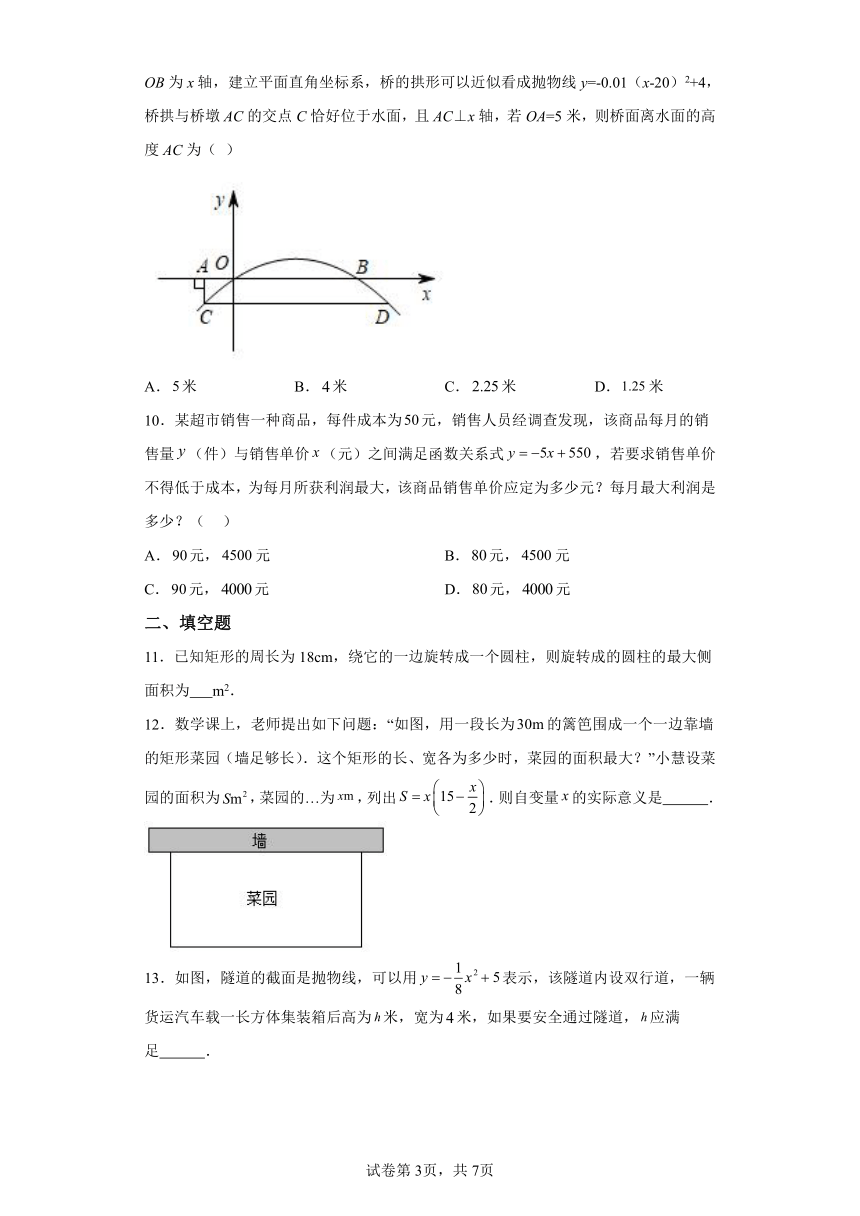
5.如图,动点P在线段上(不与点A,B重合),分别以为直径作半圆,记图中所示的阴影部分面积为y,线段的长为x.当点P从点A移动到点B时,y随x的变化而变化,则表示y与x之间关系的图象大致是( )
A. B. C. D.
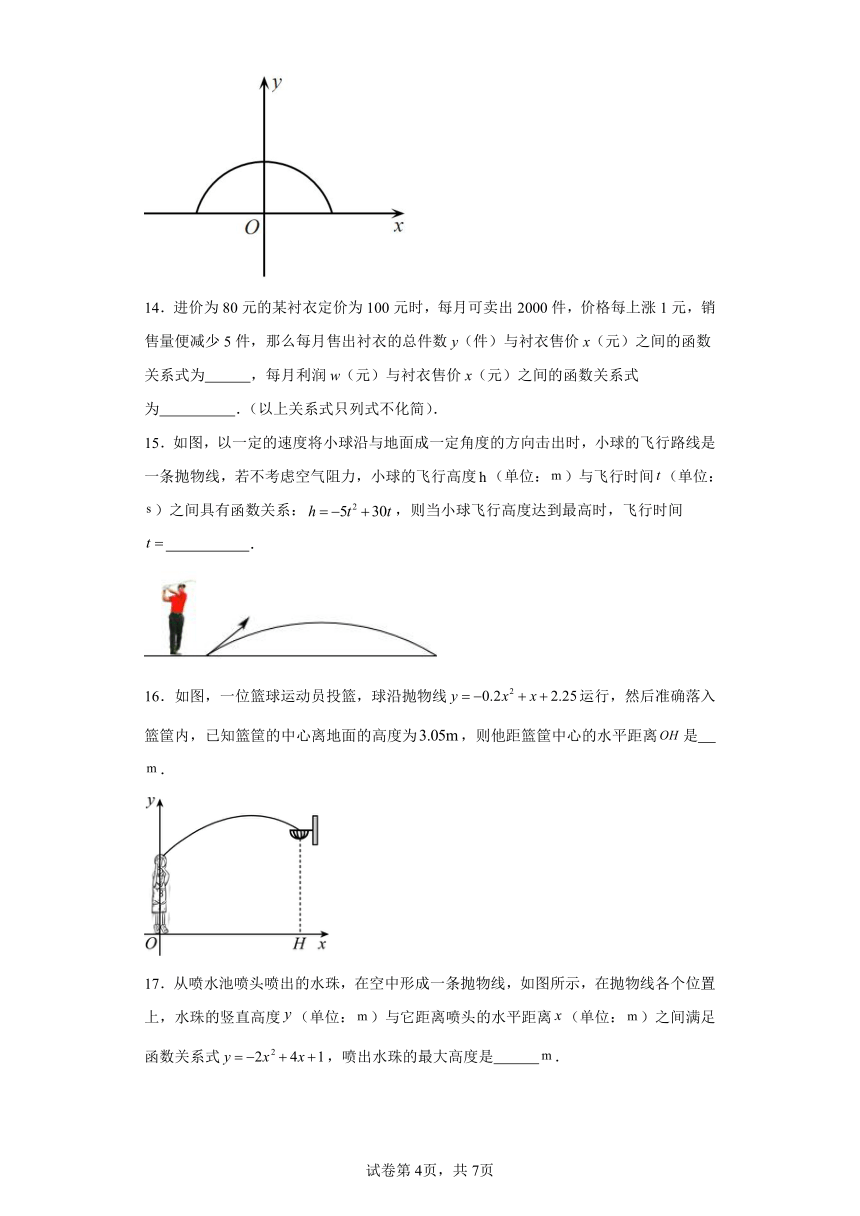
6.一座拱桥的轮廓是抛物线型(如图所示),桥高为8米,拱高6米,跨度20米.相邻两支柱间的距离均为5米,则支柱的高度为( )米.
A.米 B.3米 C.米 D.4米
7.某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(万元)与销售量x(辆)之间分别满足:,,若该公司在甲、乙两地共销售15辆该品牌的汽车,则能获得的最大利润为( )
A.30万元 B.38万元 C.46万元 D.48万元
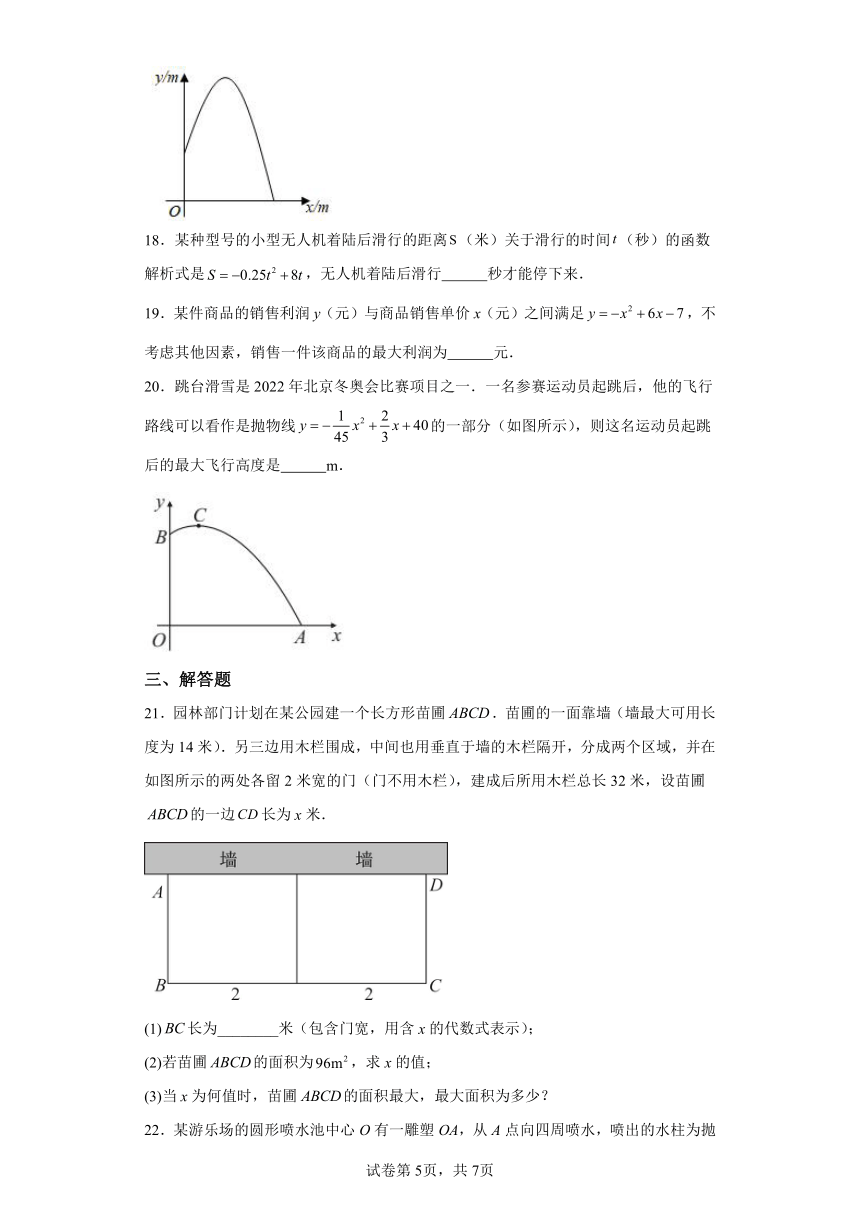
8.如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)具有函数关系为,则小球从飞出到落地的所用时间为( )
A. B. C. D.
9.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
10.某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
二、填空题
11.已知矩形的周长为18cm,绕它的一边旋转成一个圆柱,则旋转成的圆柱的最大侧面积为 m2.
12.数学课上,老师提出如下问题:“如图,用一段长为的篱笆围成一个一边靠墙的矩形菜园(墙足够长).这个矩形的长、宽各为多少时,菜园的面积最大?”小慧设菜园的面积为,菜园的…为,列出.则自变量的实际意义是 .
13.如图,隧道的截面是抛物线,可以用表示,该隧道内设双行道,一辆货运汽车载一长方体集装箱后高为米,宽为米,如果要安全通过隧道,应满足 .
14.进价为80元的某衬衣定价为100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 ,每月利润w(元)与衬衣售价x(元)之间的函数关系式为 .(以上关系式只列式不化简).
15.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线,若不考虑空气阻力,小球的飞行高度(单位:)与飞行时间(单位:)之间具有函数关系:,则当小球飞行高度达到最高时,飞行时间 .
16.如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是 .
17.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度(单位:)与它距离喷头的水平距离(单位:)之间满足函数关系式,喷出水珠的最大高度是 .
18.某种型号的小型无人机着陆后滑行的距离(米)关于滑行的时间(秒)的函数解析式是,无人机着陆后滑行 秒才能停下来.
19.某件商品的销售利润y(元)与商品销售单价x(元)之间满足,不考虑其他因素,销售一件该商品的最大利润为 元.
20.跳台滑雪是2022年北京冬奥会比赛项目之一.一名参赛运动员起跳后,他的飞行路线可以看作是抛物线的一部分(如图所示),则这名运动员起跳后的最大飞行高度是 m.
三、解答题
21.园林部门计划在某公园建一个长方形苗圃.苗圃的一面靠墙(墙最大可用长度为14米).另三边用木栏围成,中间也用垂直于墙的木栏隔开,分成两个区域,并在如图所示的两处各留2米宽的门(门不用木栏),建成后所用木栏总长32米,设苗圃的一边长为x米.
(1)长为________米(包含门宽,用含x的代数式表示);
(2)若苗圃的面积为,求x的值;
(3)当x为何值时,苗圃的面积最大,最大面积为多少?
22.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同。如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为.
(1)求落水点C、D之间的距离;
(2)若需在OD上离O点10米的E处竖立雕塑EF,,且雕塑的顶部刚好碰到水柱,求雕塑EF的高.
23.我国互联网发展走到了世界的前列,尤其是电子商务.据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)设每月获得利润为w(元),当销售单价定为多少元时,每月获得最大利润?
(2)如果每月获得8000元的利润,那么销售单价应定为多少元?;
(3)由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月销售单价不低于60元,那么每月成本最少需要多少元?
24.如图1所示的某种发石车是古代一种远程攻击的武器,发射出去的石块的运动轨迹是抛物线的一部分,且距离发射点20米时达到最大高度10米.将发石车置于山坡底部O处,山坡上有一点A,点A与点O的水平距离为30米,与地面的竖直距离为3米,AB是高度为3米的防御墙.若以点O为原点,建立如图2所示的平面直角坐标系.
(1)求石块运动轨迹所在抛物线的解析式;
(2)试通过计算说明石块能否飞越防御墙AB;
(3)在竖直方向上,试求石块飞行时与坡面OA的最大距离.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】矩形的周长为2(x+y)=10,可用x来表示y,代入S=xy中,化简即可得到S关于x的函数关系式.
【详解】解:由题意得,
2(x+y)=10,
∴x+y=5,
∴y=5﹣x,
∵S=xy
=x(5﹣x)
∴矩形面积满足的函数关系为S=x(5﹣x),
由题意可知自变量的取值范围为,
故选:A.
【点睛】本题考查了二次函数在实际问题中的应用,理清题中的数量关系并熟练掌握二次函数的解析式形式是解题的关键.
2.A
【分析】首先设抛物线解析式为y=ax2,再得出抛物线上一点为(2,﹣2),进而求出a的值.
【详解】解:由图中可以看出,所求抛物线的顶点在原点,对称轴为y轴,可设此函数解析式为:y=ax2,且抛物线过(2,﹣2)点,
故﹣2=a×22,
解得:a=﹣0.5,
故选:A.
【点睛】此题主要考查了二次函数的应用,正确设出抛物线的解析式是解题关键.
3.C
【分析】根据题意找出等量关系:总利润=单个利润×数量,即可列出函数关系式.
【详解】解:根据题意得:,
故选:C.
【点睛】本题主要考查了二次函数得实际应用,解题的关键是正确地根据题意找出等量关系列出函数表达式.
4.B
【分析】由可得抛物线的顶点坐标为:,结合函数的性质可得答案.
【详解】解:∵,
∴抛物线的顶点坐标为:,
∵,
∴实心球的最大高度是,
故选B.
【点睛】本题考查的是抛物线的图像与性质,掌握“利用顶点式求解抛物线的顶点坐标或函数的最值”是解本题的关键.
5.C
【分析】假设,则,然后根据求出y关于x的函数关系式即可得到答案.
【详解】解:假设,则,
∴
,
故选C.
【点睛】本题主要考查了二次函数在几何图形中的应用,正确求出y关于x的函数关系式是解题的关键.
6.C
【分析】设拱桥两端分别为点A、B,拱桥顶端为点C,以所在的直线为x轴,以的中点O为坐标原点,所在的直线为y轴建立平面直角坐标系,则点,点M,N的横坐标为5,再求出抛物线的解析式,即可求解.
【详解】解:如图,设拱桥两端分别为点A、B,拱桥顶端为点C,以所在的直线为x轴,以的中点O为坐标原点,所在的直线为y轴建立平面直角坐标系,则点,点M,N的横坐标为5,
设抛物线的解析式为,
把点代入得:
,解得:,
∴抛物线的解析式为,
当时,,
∴支柱的高度为米.
故选:C
【点睛】本题考查二次函数的实际应用,借助二次函数解决实际问题是解题根本,求出二次函数关系式是关键.
7.C
【分析】首先根据题意得出总利润与x之间的函数关系式,进而求出最值即可.
【详解】解:设在甲地销售x辆,则在乙地销售辆,总利润为W万元,根据题意得出:
,
∴当时,取最大值,且最大值为46,
∴该公司在甲、乙两地共销售15辆该品牌的汽车,则能获得的最大利润为46万元,故C正确.
故选:C.
【点睛】此题主要考查了二次函数的应用,解题的关键是根据题意得出函数关系式,并将函数关系式化为顶点式.
8.D
【分析】根据二次函数的图象与性质解题.
【详解】解:依题意,令得,
得,
解得(舍去)或,
即小球从飞出到落地所用的时间为,故D正确.
故选:D.
【点睛】本题主要考查二次函数的应用,熟练掌握二次函数的图象与性质是解题关键.
9.C
【分析】根据OA=5知点C的横坐标为-5,据此求出点C的纵坐标即可得出答案.
【详解】解:∵AC⊥x轴,OA=5米,
∴点C的横坐标为-5,
当x=-5时,y=-0.01(x-20)2+4=y=-0.01(-5-20)2+4=-2.25,
∴C(-5,-2.25),
∴桥面离水面的高度AC为2.25米.
故选:C.
【点睛】本题考查了二次函数的应用.解题的关键是明确题意找出所求问题需要的条件.
10.B
【分析】设每月所获利润为w,按照等量关系列出二次函数,并根据二次函数的性质求得最值即可.
【详解】解:设每月总利润为,
依题意得:
,此图象开口向下,又,
当时,有最大值,最大值为元.
故选:B.
【点睛】本题考查了二次函数在实际生活中的应用,根据题意找到等量关系并掌握二次函数求最值的方法是解题的关键.
11.π##40.5π
【分析】设矩形的长是a,宽为9-a,旋转形成的圆柱侧面积得到关于a的二次函数,根据二次函数的性质确定最大值即可.
【详解】解:设矩形的长为a,宽为9-a,
∵旋转形成的圆柱侧面积是S=2πa(9﹣a)=﹣2π(a﹣)2+π,
∴当a=时,侧面积有最大值为π,
故答案为:π
【点睛】本题考查了二次函数的应用,熟练列出二次函数并掌握求二次函数最值的方法是解题的关键.
12.平行于墙的一边的长度
【分析】根据矩形的面积公式可知,是长乘以宽,篱笆30m而根据图可知矩形只需要围3面,因此可知x是平行于墙的一边的长度.
【详解】∵矩形的面积
∴x或者是平行于墙的矩形的长
当是是平行于墙的矩形的长时,+2x≠30 ,不合题意;
当x是是平行于墙的矩形的长时,2()+x=30 ,符合合题意;
故答案为:平行于墙的一边的长度
【点睛】根据函数解析式推导自变量 x 的实际意义,理解函数解析式是解题的关键.
13.
【分析】根据,对称轴为轴,根据汽车宽为米,则当时,,即可.
【详解】∵,汽车宽为米,
∴当时,,
∴.
∵,
∴
故答案为:.
【点睛】本题考查二次函数的知识,解题的关键是掌握二次函数的图象和性质,二次函数的对称性.
14. y=2000-5(x-100) w=[2000-5(x-100)](x-80)
【解析】略
15.
【分析】将函数解析式配方为:,可以确定当小球飞行最高时,飞行时间的值.
【详解】解:∵抛物线的解析式为:,
∴抛物线的解析式为:,
∵,
∴当时,抛物线有最大值,最大值为:.
故答案为:3
【点睛】本题考查了抛物线的性质,根据抛物线解析是确定抛物线的最大值是解题的关键.
16.4
【分析】将代入中可求出x,结合图形可知,即可求出OH.
【详解】解:当时,,解得:或,
结合图形可知:,
故答案为:4
【点睛】本题考查二次函数的实际应用:投球问题,解题的关键是结合函数图形确定x的值.
17.3
【分析】把二次函数化为顶点式,进而即可求解.
【详解】解:∵,
∴当x=1时,,
故答案是:3.
【点睛】本题主要考查二次函数的图像和性质,掌握二次函数的顶点式,是解题的关键.
18.16
【分析】将函数解析式配方成顶点式求出S取得最大值时的t的值即可得答案.
【详解】解:
解:∵,
∴当时,S取得最大值64,
即飞机着陆后滑行16秒才能停下来.
故答案为:16
【点睛】本题主要考查二次函数的应用,理解题意得出飞机滑行的距离即为S的最大值是解题的关键.
19.2
【分析】知的最大值在时取得,值为.
【详解】解:
根据函数图像性质可知在时,最大且取值为
故答案为:.
【点睛】本题考查了二次函数实际应用中的最值问题.解题的关键将二次函数化成顶点式.
20.45
【分析】将抛物线表达式变换为顶点式,确定抛物线的顶点坐标,即可确定运动员起跳后的最大飞行高度.
【详解】解:抛物线,
∴抛物线顶点C的坐标为(15,45),
∴这名运动员起跳后的最大飞行高度是45m.
故答案为:45.
【点睛】本题主要考查了二次函数的应用,解题关键是能够熟练将抛物线表达式由一般式转换为顶点式.
21.(1)(36-3x)
(2)8
(3)当x为米时,苗圃ABCD的最大面积为平方米
【分析】(1)根据木栏总长32米,两处各留2米宽的门,设苗圃的一边长为x米,即得BC的长为(36-3x)米;(2)根据题意得,,即可解得x的值;(3)设苗圃的面积为w,,由二次函数的性质可得答案.
【详解】(1)∵木栏总长32米,两处各留2米宽的门,设苗圃的一边长为x米,
BC的长为32-3x+4=(36-3x)米,
故答案为:(36-3x);
(2)根据题意得,,
解得,x=4或x=8,
∵当x=4时,36-3x=24>14,
∴x=4舍去,
∴x的值为8;
(3)设苗圃的面积为w,
,
∵4<36-3x14,
∴,
∵-3<0,图象开口向下,
∴当时,w取得最大值,w最大为;
答:当x为米时,苗圃ABCD的最大面积为平方米.
【点睛】本题考查了二次函数的应用,解题的关键是读懂题意,根据已知列方程和函数关系式.
22.(1)22米
(2)雕塑EF的高为米
【分析】(1)利用二次函数图象上点的坐标特征可求出点D的坐标,进而可得出OD的长度,由喷出的水柱为抛物线且形状相同,可得出OC的长,结合CD=OC+OD即可求出落水点C,D之间的距离;
(2)代入x=10求出y值即可.
【详解】(1)解:当y=0时,,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(2)解:∵,,
当x=10时,,
∴点F(10,)
∴雕塑EF的高为米.
【点睛】本题考查了二次函数的应用,解题的关键是:(1)利用二次函数图象上点的坐标特征,求出点D的坐标;(2)利用二次函数图象上点的坐标特征,求出抛物线上横坐标为10的点的坐标.
23.(1)当销售单价定为70元时,每月获得最大利润;
(2)如果每月获得8000元的利润,那么销售单价应定为60元或80元;
(3)每月成本最少需要10000元.
【分析】(1)设,把代入即可求出一次函数的解析式,再根据总利润=单件的利润×件数即可求出每月获得利润(元)关于销售单价(元)的函数解析式,利用二次函数的性质求解即可;
(2)当时,得到,解一元二次方程即可求解;
(3)求出x的取值范围,设成本为S,根据成本=进价×销售量,即可求出S与x的函数关系式,然后利用一次函数的增减性即可求出S的最小值.
【详解】(1)解:设,把代入可得,
解得;
∴,
,
∵,抛物线的开口向下,二次函数有最大值,
∴当时,w有最大值为元,
∴当销售单价定为70元时,每月获得最大利润;
(2)解:当时,则,
解得:,;
答:如果每月获得8000元的利润,那么销售单价应定为60元或80元;
(3)解:设成本为S,
依题意得:,
∴,
∵,
∴S随x增大而减小,
∴时,S有最小值为10000元,
答:每月成本最少需要10000元.
【点睛】此题考查的是二次函数与一次函数的应用,掌握利用待定系数法求一次函数解析式和实际问题中的等量关系是解决此题的关键.
24.(1)y=﹣x2+x(0≤x≤40)
(2)能飞越,理由见解析
(3)8.1米
【分析】(1)设石块运行的函数关系式为y=a(x﹣20)2+10,用待定系数法求得a的值即可求得答案;
(2)把x=30代入y=﹣x2+x,求得y的值,与6作比较即可;
(3)用待定系数法求得OA的解析式为y=x,设抛物线上一点P(t,﹣t2+t),过点P作PQ⊥x轴,交OA于点Q,则Q(t,t),用含t的式子表示出d关于t的表达式,再利用二次函数的性质可得答案;
【详解】(1)解:设石块的运动轨迹所在抛物线的解析式为y=a(x﹣20)2+10.
把(0,0)代入,得400a+10=0,解得a=﹣.
∴y=﹣(x﹣20)2+10.即y=﹣x2+x(0≤x≤40).
(2)解:把x=30代入y=﹣x2+x,得y=﹣×900+30=7.5.
∵7.5>3+3,∴石块能飞越防御墙AB.
(3)解:设直线OA的解析式为y=kx(k≠0).
把(30,3)代入,得3=30k,
∴k=.
故直线OA的解析式为y=x.
设直线OA上方的抛物线上的一点P的坐标为(t,﹣t2+t).
过点P作PQ⊥x轴,交OA于点Q,则Q(t,t).
∴PQ=﹣t2+t﹣t=﹣t2+t=﹣(t﹣18)2+8.1.
∴当t=18时,PQ取最大值,最大值为8.1.
答:在竖直方向上,石块飞行时与坡面OA的最大距离是8.1米.
【点睛】本题考查了二次函数在实际问题中的应用,理清题中的数量关系并熟练掌握二次函数的性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,用绳子围成周长为的矩形,记矩形的一边长为,矩形的面积为.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为( )
A. B.
C. D.
2.如图(1)是一个横断面为抛物线形状的拱桥,当水面在时,拱顶(拱桥洞的最高点)离水面2 m,水面宽4 m.如图(2)建立平面直角坐标系,则抛物线的解析式是( )
A. B. C. D.
3.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价每提高2元,则每天少卖4套.设冰墩墩和雪容融套件每套售价定为x元时,则该商品每天销售套件所获利润w与x之间的函数关系式为( ).
A. B.
C. D.
4.小明在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形,若实心球运动的抛物线的表达式为,其中是实心球飞行的高度,是实心球飞行的水平距离,则小明此次郑球过程中,实心球的最大高度是( )
A. B. C. D.
5.如图,动点P在线段上(不与点A,B重合),分别以为直径作半圆,记图中所示的阴影部分面积为y,线段的长为x.当点P从点A移动到点B时,y随x的变化而变化,则表示y与x之间关系的图象大致是( )
A. B. C. D.
6.一座拱桥的轮廓是抛物线型(如图所示),桥高为8米,拱高6米,跨度20米.相邻两支柱间的距离均为5米,则支柱的高度为( )米.
A.米 B.3米 C.米 D.4米
7.某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(万元)与销售量x(辆)之间分别满足:,,若该公司在甲、乙两地共销售15辆该品牌的汽车,则能获得的最大利润为( )
A.30万元 B.38万元 C.46万元 D.48万元
8.如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)具有函数关系为,则小球从飞出到落地的所用时间为( )
A. B. C. D.
9.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
10.某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
二、填空题
11.已知矩形的周长为18cm,绕它的一边旋转成一个圆柱,则旋转成的圆柱的最大侧面积为 m2.
12.数学课上,老师提出如下问题:“如图,用一段长为的篱笆围成一个一边靠墙的矩形菜园(墙足够长).这个矩形的长、宽各为多少时,菜园的面积最大?”小慧设菜园的面积为,菜园的…为,列出.则自变量的实际意义是 .
13.如图,隧道的截面是抛物线,可以用表示,该隧道内设双行道,一辆货运汽车载一长方体集装箱后高为米,宽为米,如果要安全通过隧道,应满足 .
14.进价为80元的某衬衣定价为100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 ,每月利润w(元)与衬衣售价x(元)之间的函数关系式为 .(以上关系式只列式不化简).
15.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线,若不考虑空气阻力,小球的飞行高度(单位:)与飞行时间(单位:)之间具有函数关系:,则当小球飞行高度达到最高时,飞行时间 .
16.如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是 .
17.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度(单位:)与它距离喷头的水平距离(单位:)之间满足函数关系式,喷出水珠的最大高度是 .
18.某种型号的小型无人机着陆后滑行的距离(米)关于滑行的时间(秒)的函数解析式是,无人机着陆后滑行 秒才能停下来.
19.某件商品的销售利润y(元)与商品销售单价x(元)之间满足,不考虑其他因素,销售一件该商品的最大利润为 元.
20.跳台滑雪是2022年北京冬奥会比赛项目之一.一名参赛运动员起跳后,他的飞行路线可以看作是抛物线的一部分(如图所示),则这名运动员起跳后的最大飞行高度是 m.
三、解答题
21.园林部门计划在某公园建一个长方形苗圃.苗圃的一面靠墙(墙最大可用长度为14米).另三边用木栏围成,中间也用垂直于墙的木栏隔开,分成两个区域,并在如图所示的两处各留2米宽的门(门不用木栏),建成后所用木栏总长32米,设苗圃的一边长为x米.
(1)长为________米(包含门宽,用含x的代数式表示);
(2)若苗圃的面积为,求x的值;
(3)当x为何值时,苗圃的面积最大,最大面积为多少?
22.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同。如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为.
(1)求落水点C、D之间的距离;
(2)若需在OD上离O点10米的E处竖立雕塑EF,,且雕塑的顶部刚好碰到水柱,求雕塑EF的高.
23.我国互联网发展走到了世界的前列,尤其是电子商务.据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)设每月获得利润为w(元),当销售单价定为多少元时,每月获得最大利润?
(2)如果每月获得8000元的利润,那么销售单价应定为多少元?;
(3)由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月销售单价不低于60元,那么每月成本最少需要多少元?
24.如图1所示的某种发石车是古代一种远程攻击的武器,发射出去的石块的运动轨迹是抛物线的一部分,且距离发射点20米时达到最大高度10米.将发石车置于山坡底部O处,山坡上有一点A,点A与点O的水平距离为30米,与地面的竖直距离为3米,AB是高度为3米的防御墙.若以点O为原点,建立如图2所示的平面直角坐标系.
(1)求石块运动轨迹所在抛物线的解析式;
(2)试通过计算说明石块能否飞越防御墙AB;
(3)在竖直方向上,试求石块飞行时与坡面OA的最大距离.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】矩形的周长为2(x+y)=10,可用x来表示y,代入S=xy中,化简即可得到S关于x的函数关系式.
【详解】解:由题意得,
2(x+y)=10,
∴x+y=5,
∴y=5﹣x,
∵S=xy
=x(5﹣x)
∴矩形面积满足的函数关系为S=x(5﹣x),
由题意可知自变量的取值范围为,
故选:A.
【点睛】本题考查了二次函数在实际问题中的应用,理清题中的数量关系并熟练掌握二次函数的解析式形式是解题的关键.
2.A
【分析】首先设抛物线解析式为y=ax2,再得出抛物线上一点为(2,﹣2),进而求出a的值.
【详解】解:由图中可以看出,所求抛物线的顶点在原点,对称轴为y轴,可设此函数解析式为:y=ax2,且抛物线过(2,﹣2)点,
故﹣2=a×22,
解得:a=﹣0.5,
故选:A.
【点睛】此题主要考查了二次函数的应用,正确设出抛物线的解析式是解题关键.
3.C
【分析】根据题意找出等量关系:总利润=单个利润×数量,即可列出函数关系式.
【详解】解:根据题意得:,
故选:C.
【点睛】本题主要考查了二次函数得实际应用,解题的关键是正确地根据题意找出等量关系列出函数表达式.
4.B
【分析】由可得抛物线的顶点坐标为:,结合函数的性质可得答案.
【详解】解:∵,
∴抛物线的顶点坐标为:,
∵,
∴实心球的最大高度是,
故选B.
【点睛】本题考查的是抛物线的图像与性质,掌握“利用顶点式求解抛物线的顶点坐标或函数的最值”是解本题的关键.
5.C
【分析】假设,则,然后根据求出y关于x的函数关系式即可得到答案.
【详解】解:假设,则,
∴
,
故选C.
【点睛】本题主要考查了二次函数在几何图形中的应用,正确求出y关于x的函数关系式是解题的关键.
6.C
【分析】设拱桥两端分别为点A、B,拱桥顶端为点C,以所在的直线为x轴,以的中点O为坐标原点,所在的直线为y轴建立平面直角坐标系,则点,点M,N的横坐标为5,再求出抛物线的解析式,即可求解.
【详解】解:如图,设拱桥两端分别为点A、B,拱桥顶端为点C,以所在的直线为x轴,以的中点O为坐标原点,所在的直线为y轴建立平面直角坐标系,则点,点M,N的横坐标为5,
设抛物线的解析式为,
把点代入得:
,解得:,
∴抛物线的解析式为,
当时,,
∴支柱的高度为米.
故选:C
【点睛】本题考查二次函数的实际应用,借助二次函数解决实际问题是解题根本,求出二次函数关系式是关键.
7.C
【分析】首先根据题意得出总利润与x之间的函数关系式,进而求出最值即可.
【详解】解:设在甲地销售x辆,则在乙地销售辆,总利润为W万元,根据题意得出:
,
∴当时,取最大值,且最大值为46,
∴该公司在甲、乙两地共销售15辆该品牌的汽车,则能获得的最大利润为46万元,故C正确.
故选:C.
【点睛】此题主要考查了二次函数的应用,解题的关键是根据题意得出函数关系式,并将函数关系式化为顶点式.
8.D
【分析】根据二次函数的图象与性质解题.
【详解】解:依题意,令得,
得,
解得(舍去)或,
即小球从飞出到落地所用的时间为,故D正确.
故选:D.
【点睛】本题主要考查二次函数的应用,熟练掌握二次函数的图象与性质是解题关键.
9.C
【分析】根据OA=5知点C的横坐标为-5,据此求出点C的纵坐标即可得出答案.
【详解】解:∵AC⊥x轴,OA=5米,
∴点C的横坐标为-5,
当x=-5时,y=-0.01(x-20)2+4=y=-0.01(-5-20)2+4=-2.25,
∴C(-5,-2.25),
∴桥面离水面的高度AC为2.25米.
故选:C.
【点睛】本题考查了二次函数的应用.解题的关键是明确题意找出所求问题需要的条件.
10.B
【分析】设每月所获利润为w,按照等量关系列出二次函数,并根据二次函数的性质求得最值即可.
【详解】解:设每月总利润为,
依题意得:
,此图象开口向下,又,
当时,有最大值,最大值为元.
故选:B.
【点睛】本题考查了二次函数在实际生活中的应用,根据题意找到等量关系并掌握二次函数求最值的方法是解题的关键.
11.π##40.5π
【分析】设矩形的长是a,宽为9-a,旋转形成的圆柱侧面积得到关于a的二次函数,根据二次函数的性质确定最大值即可.
【详解】解:设矩形的长为a,宽为9-a,
∵旋转形成的圆柱侧面积是S=2πa(9﹣a)=﹣2π(a﹣)2+π,
∴当a=时,侧面积有最大值为π,
故答案为:π
【点睛】本题考查了二次函数的应用,熟练列出二次函数并掌握求二次函数最值的方法是解题的关键.
12.平行于墙的一边的长度
【分析】根据矩形的面积公式可知,是长乘以宽,篱笆30m而根据图可知矩形只需要围3面,因此可知x是平行于墙的一边的长度.
【详解】∵矩形的面积
∴x或者是平行于墙的矩形的长
当是是平行于墙的矩形的长时,+2x≠30 ,不合题意;
当x是是平行于墙的矩形的长时,2()+x=30 ,符合合题意;
故答案为:平行于墙的一边的长度
【点睛】根据函数解析式推导自变量 x 的实际意义,理解函数解析式是解题的关键.
13.
【分析】根据,对称轴为轴,根据汽车宽为米,则当时,,即可.
【详解】∵,汽车宽为米,
∴当时,,
∴.
∵,
∴
故答案为:.
【点睛】本题考查二次函数的知识,解题的关键是掌握二次函数的图象和性质,二次函数的对称性.
14. y=2000-5(x-100) w=[2000-5(x-100)](x-80)
【解析】略
15.
【分析】将函数解析式配方为:,可以确定当小球飞行最高时,飞行时间的值.
【详解】解:∵抛物线的解析式为:,
∴抛物线的解析式为:,
∵,
∴当时,抛物线有最大值,最大值为:.
故答案为:3
【点睛】本题考查了抛物线的性质,根据抛物线解析是确定抛物线的最大值是解题的关键.
16.4
【分析】将代入中可求出x,结合图形可知,即可求出OH.
【详解】解:当时,,解得:或,
结合图形可知:,
故答案为:4
【点睛】本题考查二次函数的实际应用:投球问题,解题的关键是结合函数图形确定x的值.
17.3
【分析】把二次函数化为顶点式,进而即可求解.
【详解】解:∵,
∴当x=1时,,
故答案是:3.
【点睛】本题主要考查二次函数的图像和性质,掌握二次函数的顶点式,是解题的关键.
18.16
【分析】将函数解析式配方成顶点式求出S取得最大值时的t的值即可得答案.
【详解】解:
解:∵,
∴当时,S取得最大值64,
即飞机着陆后滑行16秒才能停下来.
故答案为:16
【点睛】本题主要考查二次函数的应用,理解题意得出飞机滑行的距离即为S的最大值是解题的关键.
19.2
【分析】知的最大值在时取得,值为.
【详解】解:
根据函数图像性质可知在时,最大且取值为
故答案为:.
【点睛】本题考查了二次函数实际应用中的最值问题.解题的关键将二次函数化成顶点式.
20.45
【分析】将抛物线表达式变换为顶点式,确定抛物线的顶点坐标,即可确定运动员起跳后的最大飞行高度.
【详解】解:抛物线,
∴抛物线顶点C的坐标为(15,45),
∴这名运动员起跳后的最大飞行高度是45m.
故答案为:45.
【点睛】本题主要考查了二次函数的应用,解题关键是能够熟练将抛物线表达式由一般式转换为顶点式.
21.(1)(36-3x)
(2)8
(3)当x为米时,苗圃ABCD的最大面积为平方米
【分析】(1)根据木栏总长32米,两处各留2米宽的门,设苗圃的一边长为x米,即得BC的长为(36-3x)米;(2)根据题意得,,即可解得x的值;(3)设苗圃的面积为w,,由二次函数的性质可得答案.
【详解】(1)∵木栏总长32米,两处各留2米宽的门,设苗圃的一边长为x米,
BC的长为32-3x+4=(36-3x)米,
故答案为:(36-3x);
(2)根据题意得,,
解得,x=4或x=8,
∵当x=4时,36-3x=24>14,
∴x=4舍去,
∴x的值为8;
(3)设苗圃的面积为w,
,
∵4<36-3x14,
∴,
∵-3<0,图象开口向下,
∴当时,w取得最大值,w最大为;
答:当x为米时,苗圃ABCD的最大面积为平方米.
【点睛】本题考查了二次函数的应用,解题的关键是读懂题意,根据已知列方程和函数关系式.
22.(1)22米
(2)雕塑EF的高为米
【分析】(1)利用二次函数图象上点的坐标特征可求出点D的坐标,进而可得出OD的长度,由喷出的水柱为抛物线且形状相同,可得出OC的长,结合CD=OC+OD即可求出落水点C,D之间的距离;
(2)代入x=10求出y值即可.
【详解】(1)解:当y=0时,,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(2)解:∵,,
当x=10时,,
∴点F(10,)
∴雕塑EF的高为米.
【点睛】本题考查了二次函数的应用,解题的关键是:(1)利用二次函数图象上点的坐标特征,求出点D的坐标;(2)利用二次函数图象上点的坐标特征,求出抛物线上横坐标为10的点的坐标.
23.(1)当销售单价定为70元时,每月获得最大利润;
(2)如果每月获得8000元的利润,那么销售单价应定为60元或80元;
(3)每月成本最少需要10000元.
【分析】(1)设,把代入即可求出一次函数的解析式,再根据总利润=单件的利润×件数即可求出每月获得利润(元)关于销售单价(元)的函数解析式,利用二次函数的性质求解即可;
(2)当时,得到,解一元二次方程即可求解;
(3)求出x的取值范围,设成本为S,根据成本=进价×销售量,即可求出S与x的函数关系式,然后利用一次函数的增减性即可求出S的最小值.
【详解】(1)解:设,把代入可得,
解得;
∴,
,
∵,抛物线的开口向下,二次函数有最大值,
∴当时,w有最大值为元,
∴当销售单价定为70元时,每月获得最大利润;
(2)解:当时,则,
解得:,;
答:如果每月获得8000元的利润,那么销售单价应定为60元或80元;
(3)解:设成本为S,
依题意得:,
∴,
∵,
∴S随x增大而减小,
∴时,S有最小值为10000元,
答:每月成本最少需要10000元.
【点睛】此题考查的是二次函数与一次函数的应用,掌握利用待定系数法求一次函数解析式和实际问题中的等量关系是解决此题的关键.
24.(1)y=﹣x2+x(0≤x≤40)
(2)能飞越,理由见解析
(3)8.1米
【分析】(1)设石块运行的函数关系式为y=a(x﹣20)2+10,用待定系数法求得a的值即可求得答案;
(2)把x=30代入y=﹣x2+x,求得y的值,与6作比较即可;
(3)用待定系数法求得OA的解析式为y=x,设抛物线上一点P(t,﹣t2+t),过点P作PQ⊥x轴,交OA于点Q,则Q(t,t),用含t的式子表示出d关于t的表达式,再利用二次函数的性质可得答案;
【详解】(1)解:设石块的运动轨迹所在抛物线的解析式为y=a(x﹣20)2+10.
把(0,0)代入,得400a+10=0,解得a=﹣.
∴y=﹣(x﹣20)2+10.即y=﹣x2+x(0≤x≤40).
(2)解:把x=30代入y=﹣x2+x,得y=﹣×900+30=7.5.
∵7.5>3+3,∴石块能飞越防御墙AB.
(3)解:设直线OA的解析式为y=kx(k≠0).
把(30,3)代入,得3=30k,
∴k=.
故直线OA的解析式为y=x.
设直线OA上方的抛物线上的一点P的坐标为(t,﹣t2+t).
过点P作PQ⊥x轴,交OA于点Q,则Q(t,t).
∴PQ=﹣t2+t﹣t=﹣t2+t=﹣(t﹣18)2+8.1.
∴当t=18时,PQ取最大值,最大值为8.1.
答:在竖直方向上,石块飞行时与坡面OA的最大距离是8.1米.
【点睛】本题考查了二次函数在实际问题中的应用,理清题中的数量关系并熟练掌握二次函数的性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
