专题22.34实际问题与二次函数 直通中考培优练(含解析)2023-2024学年九年级数学上册人教版专项讲练
文档属性
| 名称 | 专题22.34实际问题与二次函数 直通中考培优练(含解析)2023-2024学年九年级数学上册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 23:10:31 | ||
图片预览




文档简介
专题22.34 实际问题与二次函数(直通中考)(培优练)
(2023·四川南充·统考中考真题)
1.某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件.已知A产品成本价m元/件(m为常数,且,售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式
(1)若产销A,B两种产品的日利润分别为元,元,请分别写出,与x的函数关系式,并写出x的取值范围;
(2)分别求出产销A,B两种产品的最大日利润.(A产品的最大日利润用含m的代数式表示)
(3)为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.【利润(售价成本)产销数量专利费】
(2023·浙江温州·统考中考真题)
2.一次足球训练中,小明从球门正前方的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为时,球达到最高点,此时球离地面.已知球门高为2.44m,现以O为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素).
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方2.25m处?
(2023·湖北黄冈·统考中考真题)
3.加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元/.
(1)当___________时,元/;
(2)设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?
(3)学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降,乙种蔬菜种植成本平均每年下降,当a为何值时,2025年的总种植成本为元?
(2023·湖北武汉·统考中考真题)
4.某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离(单位:)以、飞行高度(单位:)随飞行时间(单位:)变化的数据如下表.
飞行时间 0 2 4 6 8 …
飞行水平距离 0 10 20 30 40 …
飞行高度 0 22 40 54 64 …
探究发现:与,与之间的数量关系可以用我们已学过的函数来描述.直接写出关于的函数解析式和关于的函数解析式(不要求写出自变量的取值范围).
问题解决:如图,活动小组在水平安全线上处设置一个高度可以变化的发射平台试飞该航模飞机.根据上面的探究发现解决下列问题.
(1)若发射平台相对于安全线的高度为0m,求飞机落到安全线时飞行的水平距离;
(2)在安全线上设置回收区域.若飞机落到内(不包括端点),求发射平台相对于安全线的高度的变化范围.
(2023·山东·统考中考真题)
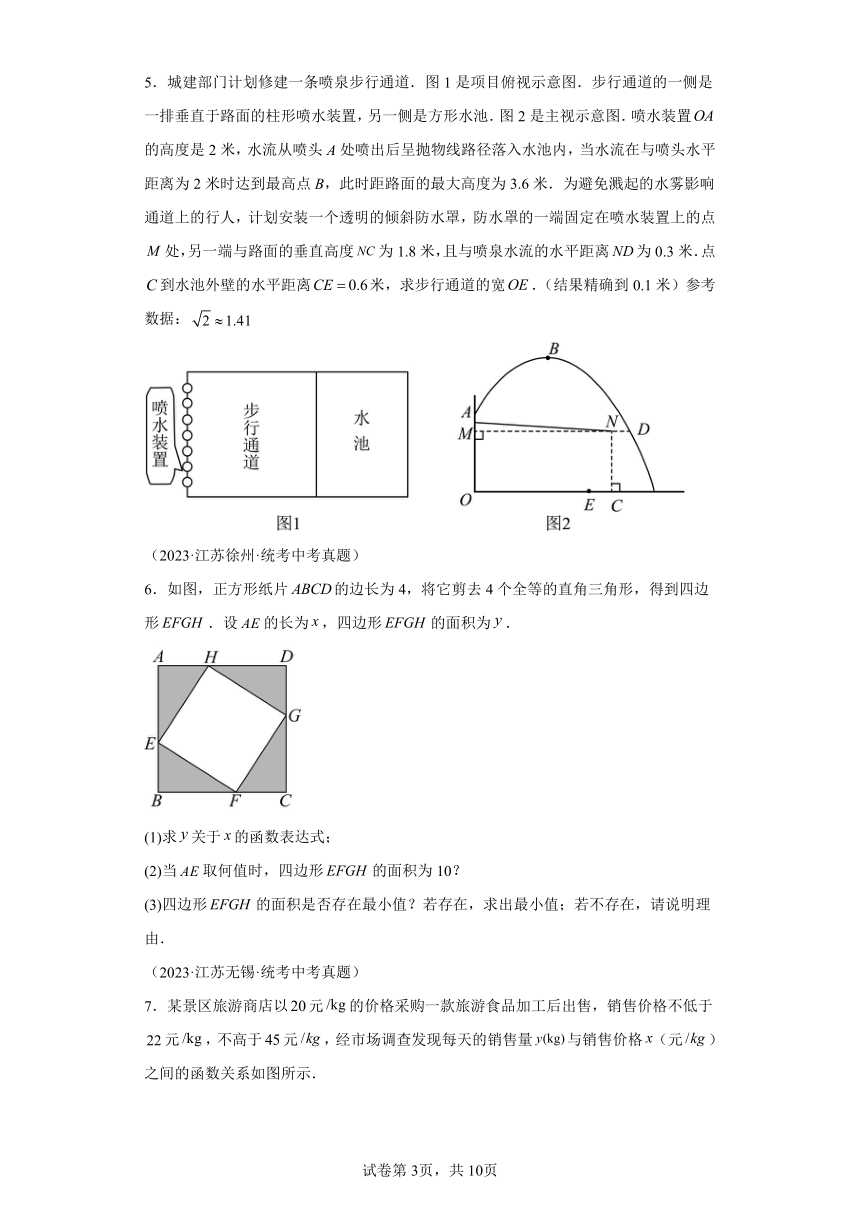
5.城建部门计划修建一条喷泉步行通道.图1是项目俯视示意图.步行通道的一侧是一排垂直于路面的柱形喷水装置,另一侧是方形水池.图2是主视示意图.喷水装置的高度是2米,水流从喷头A处喷出后呈抛物线路径落入水池内,当水流在与喷头水平距离为2米时达到最高点B,此时距路面的最大高度为3.6米.为避免溅起的水雾影响通道上的行人,计划安装一个透明的倾斜防水罩,防水罩的一端固定在喷水装置上的点处,另一端与路面的垂直高度为1.8米,且与喷泉水流的水平距离为0.3米.点到水池外壁的水平距离米,求步行通道的宽.(结果精确到0.1米)参考数据:
(2023·江苏徐州·统考中考真题)
6.如图,正方形纸片的边长为4,将它剪去4个全等的直角三角形,得到四边形.设的长为,四边形的面积为.
(1)求关于的函数表达式;
(2)当取何值时,四边形的面积为10?
(3)四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
(2023·江苏无锡·统考中考真题)
7.某景区旅游商店以元的价格采购一款旅游食品加工后出售,销售价格不低于元,不高于元,经市场调查发现每天的销售量与销售价格(元)之间的函数关系如图所示.
(1)求关于的函数表达式:
(2)当销售价格定为多少时,该商店销售这款食品每天获得的销售利润最大?最大销售利润是多少?【销售利润=(销售价格一采购价格)×销售量】
(2023·辽宁·统考中考真题)
8.商店出售某品牌护眼灯,每台进价为40元,在销售过程中发现,月销量(台)与销售单价(元)之间满足一次函数关系,规定销售单价不低于进价,且不高于进价的2倍,其部分对应数据如下表所示:
销售单价(元) … 50 60 70 …
月销量(台) … 90 80 70 …
(1)求y与x之间的函数关系式;
(2)当护眼灯销售单价定为多少元时,商店每月出售这种护眼灯所获的利润最大?最大月利润为多少元?
(2023·内蒙古·统考中考真题)
9.随着科技的发展,扫地机器人已广泛应用于生活中,某公司推出一款新型扫地机器人,经统计该产品2022年每个月的销售情况发现,每台的销售价格随销售月份的变化而变化、设该产品2022年第(为整数)个月每台的销售价格为(单位:元),与的函数关系如图所示(图中为一折线).
(1)当时,求每台的销售价格与之间的函数关系式;
(2)设该产品2022年第个月的销售数量为(单位:万台),m与的关系可以用来描述,求哪个月的销售收入最多,最多为多少万元?(销售收入每台的销售价格销售数量)
(2023·湖北·统考中考真题)
10.某商店销售某种商品的进价为每件30元,这种商品在近60天中的日销售价与日销售量的相关信息如下表:
时间:第x(天)
日销售价(元/件) 50
日销售量(件)
(,x为整数)
设该商品的日销售利润为w元.
(1)直接写出w与x的函数关系式__________________;
(2)该商品在第几天的日销售利润最大?最大日销售利润是多少?
(2023·甘肃兰州·统考中考真题)
11.一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离的长.
(2023·山东·统考中考真题)
12.某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为A,B两块(如图所示),花园里种满牡丹和芍药,学校已定购篱笆120米.
(1)设计一个使花园面积最大的方案,并求出其最大面积;
(2)在花园面积最大的条件下,A,B两块内分别种植牡丹和芍药,每平方米种植2株,知牡丹每株售价25元,芍药每株售价15元,学校计划购买费用不超过5万元,求最多可以购买多少株牡丹?
(2023·河南·统考中考真题)
13.小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.
如图,在平面直角坐标系中,点A,C在x轴上,球网与y轴的水平距离,,击球点P在y轴上.若选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系;若选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系.
(1)求点P的坐标和a的值.
(2)小林分析发现,上面两种击球方式均能使球过网.要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式.
(2023·湖北随州·统考中考真题)
14.为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为,已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元
(1)___________, ___________;
(2)求第x天的销售额W元与x之间的函数关系式;
(3)在试销售的30天中,销售额超过1000元的共有多少天?
(2023·河北·统考中考真题)
15.嘉嘉和淇淇在玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.
如图,在平面直角坐标系中,一个单位长度代表1m长.嘉嘉在点处将沙包(看成点)抛出,并运动路线为抛物线的一部分,淇淇恰在点处接住,然后跳起将沙包回传,其运动路线为抛物线的一部分.
(1)写出的最高点坐标,并求a,c的值;
(2)若嘉嘉在x轴上方的高度上,且到点A水平距离不超过的范围内可以接到沙包,求符合条件的n的整数值.
(2023·湖北十堰·统考中考真题)
16.“端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为p盒.
(1)当时,__________;
(2)当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?
(3)小强说:“当日销售利润最大时,日销售额不是最大,”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为.”你认为他们的说法正确吗?若正确,请说明理由;若不正确,请直接写出正确的结论.
(2023·辽宁·统考中考真题)
17.电商平台销售某款儿童组装玩具,进价为每件100元,在销售过程中发现,每周的销售量y(件)与每件玩具售价x(元)之间满足一次函数关系(其中,且x为整数).当每件玩具售价为120元时,每周的销量为80件;当每件玩具售价为140元时,每周的销量为40件.
(1)求y与x之间的函数关系式;
(2)当每件玩具售价为多少元时,电商平台每周销售这款玩具所获的利润最大?最大周利润是多少元?
(2023·江苏宿迁·统考中考真题)
18.某商场销售两种商品,每件进价均为20元.调查发现,如果售出种20件,种10件,销售总额为840元;如果售出种10件,种15件,销售总额为660元.
(1)求两种商品的销售单价.
(2)经市场调研,种商品按原售价销售,可售出40件,原售价每降价1元,销售量可增加10件;种商品的售价不变,种商品售价不低于种商品售价.设种商品降价元,如果两种商品销售量相同,求取何值时,商场销售两种商品可获得总利润最大?最大利润是多少?
(2023·黑龙江大庆·统考中考真题)
19.某建筑物的窗户如图所示,上半部分是等腰三角形,,,点、、分别是边、、的中点;下半部分四边形是矩形,,制造窗户框的材料总长为16米(图中所有黑线的长度和),设米,米.
(1)求与之间的函数关系式,并求出自变量的取值范围;
(2)当为多少时,窗户透过的光线最多(窗户的面积最大),并计算窗户的最大面积.
(2023·山东潍坊·统考中考真题)
20.工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量,,与之间的距离为2米,米,米,,.,,是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?
(2023·辽宁营口·统考中考真题)
21.某大型超市购进一款热销的消毒洗衣液,由于原材料价格上涨,今年每瓶洗衣液的进价比去年每瓶洗衣液的进价上涨4元,今年用1440元购进这款洗衣液的数量与去年用1200元购进这款洗衣液的数量相同.当每瓶洗衣液的现售价为36元时,每周可卖出600瓶,为了能薄利多销.该超市决定降价销售,经市场调查发现,这种洗衣液的售价每降价1元,每周的销量可增加100瓶,规定这种消毒洗衣液每瓶的售价不低于进价.
(1)求今年这款消毒洗衣液每瓶进价是多少元;
(2)当这款消毒洗衣液每瓶的售价定为多少元时,这款洗衣液每周的销售利润最大?最大利润是多少元?
(2023·湖南益阳·统考中考真题)
22.某企业准备对A,B两个生产性项目进行投资,根据其生产成本、销售情况等因素进行分析得知:投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:,投资B项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:.
(1)若将10万元资金投入A项目,一年后获得的收益是多少?
(2)若对A,B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,则m的值是多少?
(3)2023年,我国对小微企业施行所得税优惠政策.该企业将根据此政策获得的减免税款及其他结余资金共计32万元,全部投入到A,B两个项目中,当A,B两个项目分别投入多少万元时,一年后获得的收益之和最大?最大值是多少万元?
(2023·江苏泰州·统考中考真题)
23.某公司的化工产品成本为30元/千克.销售部门规定:一次性销售1000千克以内时,以50元/千克的价格销售;一次性销售不低于1000千克时,每增加1千克降价元.考虑到降价对利润的影响,一次性销售不低于1750千克时,均以某一固定价格销售.一次性销售利润y(元)与一次性销售量x(千克)的函数关系如图所示.
(1)当一次性销售800千克时利润为多少元?
(2)求一次性销售量在之间时的最大利润;
(3)当一次性销售多少千克时利润为22100元?
(2023·贵州·统考中考真题)
24.如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在处,对称轴与水平线垂直,,点在抛物线上,且点到对称轴的距离,点在抛物线上,点到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在上找一点,加装拉杆,同时使拉杆的长度之和最短,请你帮小星找到点的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为,当时,函数的值总大于等于9.求的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1),
(2)元,
(3)当时,该工厂应该选择产销A产品能获得最大日利润;当时,该工厂应该选择产销任一产品都能获得最大日利润;当时,该工厂应该选择产销B产品能获得最大日利润,理由见解析
【分析】(1)根据题木所给的利润计算公式求解即可;
(2)根据(1)所求利用一次函数和二次函数的性质求解即可;
(3)比较(2)中所求A、B两种产品的最大利润即可得到答案.
【详解】(1)解:由题意得,,
(2)解:∵,
∴,
∴随x增大而增大,
∴当时,最大,最大为元;
,
∵,
∴当时,随x增大而增大,
∴当时,最大,最大为元;
(3)解:当,即时,该工厂应该选择产销A产品能获得最大日利润;
当,即时,该工厂应该选择产销任一产品都能获得最大日利润;
当,即时,该工厂应该选择产销B产品能获得最大日利润;
综上所述,当时,该工厂应该选择产销A产品能获得最大日利润;当时,该工厂应该选择产销任一产品都能获得最大日利润;当时,该工厂应该选择产销B产品能获得最大日利润.
【点睛】本题主要考查了一次函数的实际应用,二次函数的实际应用,一元一次不等式的实际应用,正确理解题意列出对应的函数关系式是解题的关键.
2.(1),球不能射进球门
(2)当时他应该带球向正后方移动1米射门
【分析】(1)根据建立的平面直角三角坐标系设抛物线解析式为顶点式,代入A点坐标求出a的值即可得到函数表达式,再把代入函数解析式,求出函数值,与球门高度比较即可得到结论;
(2)根据二次函数平移的规律,设出平移后的解析式,然后将点代入即可求解.
【详解】(1)解:由题意得:抛物线的顶点坐标为,
设抛物线解析式为,
把点代入,得,
解得,
∴抛物线的函数表达式为,
当时,,
∴球不能射进球门;
(2)设小明带球向正后方移动米,则移动后的抛物线为,
把点代入得,
解得(舍去),,
∴当时他应该带球向正后方移动1米射门.
【点睛】此题考查了二次函数的应用,待定系数法求函数解析式、二次函数图象的平移等知识,读懂题意,熟练掌握待定系数法是解题的关键.
3.(1)
(2)当甲种蔬菜的种植面积为,乙种蔬菜的种植面积为时,W最小;
(3)当a为时,2025年的总种植成本为元.
【分析】(1)求出当时,设甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系式为,当时,,求出当时的x的值即可;
(2)当时,,由二次函数性质得到当时,有最小值,最小值为,当时,由一次函数性质得到当时,有最小值,最小值为,比较后即可得到方案;
(3)根据2025年的总种植成本为元列出一元二次方程,解方程即可得到答案.
【详解】(1)解:当时,设甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系式为,把点代入得,
,
解得,
∴当时,,
当时,,
∴当时,,解得,
即当时,元/;
故答案为:;
(2)解:当时,,
∵,
∴抛物线开口向上,
∴当时,有最小值,最小值为,
当时,,
∵,
∴随着x的增大而减小,
∴当时,有最小值,最小值为,
综上可知,当甲种蔬菜的种植面积为,乙种蔬菜的种植面积为时,W最小;
(3)由题意可得,
解得(不合题意,舍去),
∴当a为时,2025年的总种植成本为元.
【点睛】此题考查了二次函数的应用、一元二次方程的应用、一次函数的应用等知识,读懂题意,正确列出函数解析式和方程是解题的关键.
4.探索发现:;问题解决:(1);(2)大于且小于
【分析】探究发现:根据待定系数法求解即可;
问题解决:(1)令二次函数代入函数解析式即可求解;
(2)设发射平台相对于安全线的高度为,则飞机相对于安全线的飞行高度.结合,即可求解.
【详解】探究发现:x与t是一次函数关系,y与t是二次函数关系,
设,,
由题意得:,,
解得:,
∴.
问题解决(1) 解:依题总,得.
解得,(舍),,
当时,.
答:飞机落到安全线时飞行的水平距离为.
(2)解:设发射平台相对于安全线的高度为,飞机相对于安全线的飞行高度.
,
,
,
在中,
当时,;
当时,.
.
答:发射平台相对于安全线的高度的变化范围是大于且小于.
【点睛】本题考查了一次函数与二次函数的应用,利用待定系数法求函数的解析式,关键是把实际问题分析转变成数学模型.
5.3.2米
【分析】先以点O为坐标原点,所在直线为x轴,所在直线为y轴,建立平面直角坐标系,则,,设设抛物线的解析式为,把代入,求得,即,再求出点D的坐标,即可求解.
【详解】解:如图,建立平面直角坐标系,
由题意知:,,
∵抛物线的最高点B,
∴设抛物线的解析式为,
把代入,得,
解得,
∴抛物线的解析式为,
令,则,
解得:,
∴,
∴ (米),
答:步行通道的宽的长约为3.2米.
【点睛】本题考查抛物线的实际应用.熟练掌握用待定系数法求抛物线解析式和抛物线的图象性质是解题的关键.
6.(1)
(2)当取1或3时,四边形的面积为10;
(3)存在,最小值为8.
【分析】(1)先证出四边形为正方形,用未知数x表示其任一边长,根据正方形面积公式即可解决问题;
(2)代入y值,解一元二次方程即可;
(3)把二次函数配方化为顶点式,结合其性质即可求出最小值.
【详解】(1)解:在正方形纸片上剪去4个全等的直角三角形,
,
,四边形为正方形,
在中,,
,
正方形的面积;
不能为负,
,
故关于的函数表达式为
(2)解:令,得,
整理,得,
解得,
故当取1或3时,四边形的面积为10;
(3)解:存在.
正方形的面积;
当时,y有最小值8,即四边形的面积最小为8.
【点睛】本题考查二次函数的应用.解题的关键是找准数量关系,对于第三问,只需把二次函数表达式配方化为顶点式,即可求解.
7.(1)
(2)销售价格为元时,利润最大为
【分析】(1)分时,当时,分别待定系数法求解析式即可求解;
(2)设利润为,根据题意当时,得出,当时,,
进而根据分时,当时,分别求得最大值,即可求解.
【详解】(1)当时,设关于的函数表达式为,将点代入得,
∴
解得:
∴,
当时,设关于的函数表达式为,将点代入得,
解得:
∴,
(2)设利润为
当时,
∵在范围内,随着的增大而增大,
当时,取得最大值为;
当时,
∴当时,w取得最大值为
,
当销售价格为元时,利润最大为.
【点睛】本题考查了一次函数的应用,二次函数的应用,根据题意列出函数关系式是解题的关键.
8.(1)
(2)护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获的利润最大,最大月利润为2400元
【分析】(1)用待定系数法求解即可;
(2)设销售利润为W元,列出W关于x的函数关系式,即可求得最大利润.
【详解】(1)解:由题意设,
由表知,当时,;当时,;
以上值代入函数解析式中得:,
解得:,
所以y与x之间的函数关系式为;
(2)解:设销售利润为W元,
则,
整理得:,
由于销售单价不低于进价,且不高于进价的2倍,则,
∵,,
∴当时,W随x的增大而增大,
∴当时,W有最大值,且最大值为2400;
答:当护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获的利润最大,最大月利润为2400元.
9.(1)
(2)第5个月的销售收入最多,最多为3375万元
【分析】(1)利用待定系数法即可求解;
(2)根据销售收入每台的销售价格销售数量求得销售收入为万元与销售月份之间的函数关系,再利用函数的性质即可求解.
【详解】(1)解:当时,设每台的销售价格与之间的函数关系式为.
∵图象过两点,
,解得
∴当时,每台的销售价格与之间的函数关系式为.
(2)设销售收入为万元,
①当时,,
,当时,(万元).
②当时,,
,
∴随的增大而增大,
∴当时,(万元).
,∴第5个月的销售收入最多,最多为3375万元.
【点睛】本题考查了待定系数法求一次函数的解析式、二次函数在销售问题中的应用,理清题中的数量关系并熟练掌握二次函数的性质是解题的关键.
10.(1)
(2)该商品在第26天的日销售利润最大,最大日销售利润是1296元
【分析】(1)根据利润=单个利润×数量可进行求解;
(2)由(1)分别求出两种情况下的最大利润,然后问题可求解.
【详解】(1)解:由题意得:
当时,则;
当时,则;
∴;
(2)解:当时,;
∵抛物线开口向下,对称轴为直线,
∴当时,(元).
当时,,随增大而减小,
∴当时,(元).
∵,
∴该商品在第26天的日销售利润最大,最大日销售利润是1296元.
【点睛】本题主要考查二次函数与一次函数的应用,熟练掌握一次函数与二次函数的性质是解题的关键.
11.(1)y关于x的函数表达式为;
(2)运动员从起跳点到入水点的水平距离的长为.
【分析】(1)由题意得抛物线的对称轴为,经过点,,利用待定系数法即可求解;
(2)令,解方程即可求解.
【详解】(1)解:由题意得抛物线的对称轴为,经过点,,
设抛物线的表达式为,
∴,解得,
∴y关于x的函数表达式为;
(2)解:令,则,
解得(负值舍去),
∴运动员从起跳点到入水点的水平距离的长为.
【点睛】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握运用待定系数法求抛物线的解析式是解题的关键.
12.(1)长为60米,宽为20米时,有最大面积,且最大面积为1200平方米
(2)最多可以购买1400株牡丹
【分析】(1)设长为x米,面积为y平方米,则宽为米,可以得到y与x的函数关系式,配成顶点式求出函数的最大值即可;
(2)设种植牡丹的面积为a平方米,则种植芍药的面积为平方米,由题意列出不等式求得种植牡丹面积的最大值,即可解答.
【详解】(1)解:设长为x米,面积为y平方米,则宽为米,
∴,
∴当时,y有最大值是1200,
此时,宽为(米)
答:长为60米,宽为20米时,有最大面积,且最大面积为1200平方米.
(2)解:设种植牡丹的面积为a平方米,则种植芍药的面积为平方米,
由题意可得
解得:,
即牡丹最多种植700平方米,
(株),
答:最多可以购买1400株牡丹.
【点睛】本题考查二次函数的应用、一元一次不等式的应用,解题的关键是明确题意,找出所求问题需要的条件.
13.(1),,
(2)选择吊球,使球的落地点到C点的距离更近
【分析】(1)在一次函数上,令,可求得,再代入即可求得的值;
(2)由题意可知,令,分别求得,,即可求得落地点到点的距离,即可判断谁更近.
【详解】(1)解:在一次函数,
令时,,
∴,
将代入中,可得:,
解得:;
(2)∵,,
∴,
选择扣球,则令,即:,解得:,
即:落地点距离点距离为,
∴落地点到C点的距离为,
选择吊球,则令,即:,解得:(负值舍去),
即:落地点距离点距离为,
∴落地点到C点的距离为,
∵,
∴选择吊球,使球的落地点到C点的距离更近.
【点睛】本题考查二次函数与一次函数的应用,理解题意,求得函数解析式是解决问题的关键.
14.(1),
(2)时,,当时,
(3)7天
【分析】(1)利用待定系数法求待定系数;
(2)根据“销售额=售价×销售量”列出函数关系式,
(3)利用二次函数和一次函数的性质分析求解.
【详解】(1)解:∵第5天售价为50元/千克,第10天售价为40元/千克,
∴,解得,
故答案为:,;
(2)解:由题意当时,,
当时,,
(3)解:由题意当时,,
∵,
∴当时,最大为,
当时,,
由时,解得,
又∵x为整数,且,
∴当时,随的增大而增大,
∴第至天,销售额超过1000元,共7天.
【点睛】本题考查一次函数的应用,二次函数的应用,理解题意,分段分析函数解析式,掌握一次函数和二次函数的性质是解题关键.
15.(1)的最高点坐标为,,;
(2)符合条件的n的整数值为4和5.
【分析】(1)利用顶点式即可得到最高点坐标;点在抛物线上,利用待定系数法即可求得a的值;令,即可求得c的值;
(2)求得点A的坐标范围为,求得n的取值范围,即可求解.
【详解】(1)解:∵抛物线,
∴的最高点坐标为,
∵点在抛物线上,
∴,解得:,
∴抛物线的解析式为,令,则;
(2)解:∵到点A水平距离不超过的范围内可以接到沙包,
∴点A的坐标范围为,
当经过时,,
解得;
当经过时,,
解得;
∴
∴符合条件的n的整数值为4和5.
【点睛】本题考查了二次函数的应用,联系实际,读懂题意,熟练掌握二次函数图象上点的坐标特征是解题的关键.
16.(1)
(2)当每盒售价定为65元时,日销售利润W(元)最大,最大利润是元.
(3)他们的说法正确,理由见解析
【分析】(1)根据每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,列式计算即可;
(2)根据销售量乘以每盒的利润得到,根据二次函数的性质即可得到答案;
(3)设日销售额为元,则,根据二次函数的性质即可判断当日销售利润最大时,日销售额不是最大,即可判断小强的说法;当时,由,解得,由抛物线开口向下,得到当时,,即可判断小红的说法.
【详解】(1)解:当时,(盒),
故答案为:
(2)由题意得,
,
又∵,即,
解得,
∵,
∴当时,W最大,最大值为,
∴当每盒售价定为65元时,日销售利润W(元)最大,最大利润是元.
(3)他们的说法正确,理由如下:
设日销售额为元,则
,
∵,
∴当时,最大,最大值为,
∴当时,最大,此时为,
即小强的说法正确;
当时,,解得,
∵抛物线开口向下,
∴当时,∵,
∴当日销售利润不低于元时,每盒售价x的范围为.
故小红的说法错误.
【点睛】此题考查了二次函数的应用,根据题意正确列出函数解析式是基础,熟练掌握二次函数的性质和正确计算是解题的关键.
17.(1)(其中,且x为整数)
(2)当每件玩具售价为130元时,电商平台每周销售这款玩具所获的利润最大,最大周利润是1800元
【分析】(1)设y与x之间的函数关系式为,利用待定系数法求解即可;
(2)设每周销售这款玩具所获的利润为W,列出W关于x的二次函数关系式,化为顶点式即可求解.
【详解】(1)解:设y与x之间的函数关系式为,
由已知得,
解得,
因此y与x之间的函数关系式为(其中,且x为整数);
(2)解:设每周销售这款玩具所获的利润为W,
由题意得,
,
W关于x的二次函数图象开口向上,
,且x为整数,
当时,W取最大值,最大值为1800,
即当每件玩具售价为130元时,电商平台每周销售这款玩具所获的利润最大,最大周利润是1800元.
【点睛】本题考查一次函数与二次函数的实际应用,列出周利润W关于x的二次函数关系式是解题的关键.
18.(1)的销售单价为元、的销售单价为元
(2)当时,商场销售两种商品可获得总利润最大,最大利润是元.
【分析】(1)设的销售单价为元、的销售单价为元,根据题中售出种20件,种10件,销售总额为840元;售出种10件,种15件,销售总额为660元列方程组求解即可得到答案;
(2)设利润为,根据题意,得到,结合二次函数性质及题中限制条件分析求解即可得到答案.
【详解】(1)解:设的销售单价为元、的销售单价为元,则
,解得,
答:的销售单价为元、的销售单价为元;
(2)解:种商品售价不低于种商品售价,
,解得,即,
设利润为,则
,
,
在时能取到最大值,最大值为,
当时,商场销售两种商品可获得总利润最大,最大利润是元.
【点睛】本题考查二元一次方程组及二次函数解实际应用题,读懂题意,根据等量关系列出方程组,根据函数关系找到函数关系式分析是解决问题的关键.
19.(1)
(2)当时,窗户透过的光线最多(窗户的面积最大),最大面积为.
【分析】(1)由可表示出的长,由,可表示出,,,,,的长,进而可求出与之间的函数关系式;
(2)根据(1)中相关数据列出函数解析式,然后利用函数的性质解答.
【详解】(1)∵四边形是矩形,
∴,
∵,
∴.
∵,是边的中点,
∴,,
∵,
∴,
∴.
∵点、、分别是边、的中点,
∴,
∴,
∴,
∴,
∵,
∴,
∴;
(2)设面积为S,
则
,
∴当时,窗户透过的光线最多(窗户的面积最大),最大面积为.
【点睛】本题考查了一次函数的应用,二次函数的应用,正确列出函数解析式是解答本题的关键.
20.当的长度为米时,矩形铁皮的面积最大,最大面积是平方米
【分析】连接,分别交于点,交于点,先判断出四边形是矩形,从而可得,再判断出四边形和四边形都是矩形,从而可得米,,然后设矩形的面积为平方米,米,则米,米,利用矩形的面积公式可得关于的二次函数,最后利用二次函数的性质求解即可得.
【详解】解:如图,连接,分别交于点,交于点,
,
,
米,
四边形是平行四边形,
又,
四边形是矩形,
,,
,
,
四边形是矩形,
,
四边形和四边形都是矩形,
米,,
和都是等腰直角三角形,
,
,
设矩形的面积为平方米,米,则米,米,
米,
米,
,
又,与之间的距离为2米,米,
,
由二次函数的性质可知,当时,随的增大而增大;当时,随的增大而减小,
则当时,取得最大值,最大值为,
答:当的长度为米时,矩形铁皮的面积最大,最大面积是平方米.
【点睛】本题考查了二次函数的几何应用、矩形的判定与性质等知识点,熟练掌握二次函数的性质是解题关键.
21.(1)今年这款消毒洗衣液每瓶进价是24元;
(2)当这款消毒洗衣液每瓶的售价定为33元时,这款洗衣液每周的销售利润最大,最大利润是8100元.
【分析】(1)设今年这款消毒洗衣液每瓶进价是x元,则去年这款消毒洗衣液每瓶进价是元,根据题意列出分式方程,解方程即可;
(2)设这款消毒洗衣液每瓶的售价定为m元时,这款洗衣液每周的销售利润w最大,根据题意得出:,根据二次函数的性质可得出答案.
【详解】(1)解:设今年这款消毒洗衣液每瓶进价是x元,则去年这款消毒洗衣液每瓶进价是元,
根据题意可得:,
解得:,
经检验:是方程的解,
元,
答:今年这款消毒洗衣液每瓶进价是24元.
(2)解:设这款消毒洗衣液每瓶的售价定为m元时,这款洗衣液每周的销售利润w最大,
根据题意得出:,
整理得:,
根据二次函数的性质得出:当时,利润最大,
最大利润为:,
答:当这款消毒洗衣液每瓶的售价定为33元时,这款洗衣液每周的销售利润最大,最大利润是8100元.
【点睛】本题考查分式方程的应用,二次函数的应用,正确理解题意列出关系式是解题关键.
22.(1)4万元
(2)
(3)当A,B两个项目分别投入28万,4万元时,一年后获得的收益之和最大,最大值是16万元.
【分析】(1)把代入可得答案;
(2)当时,可得,再解方程可得答案;
(3)设投入到B项目的资金为万元,则投入到A项目的资金为万元,设总收益为y万元,,而,再利用二次函数的性质可得答案.
【详解】(1)解:∵投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:,
当时,(万元);
(2)∵对A,B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,
∴,
整理得:,
解得:,(不符合题意),
∴m的值为8.
(3)
设投入到B项目的资金为万元,则投入到A项目的资金为万元,设总收益为y万元,
∴
,
而,
∴当时,(万元);
∴当A,B两个项目分别投入28万,4万元时,一年后获得的收益之和最大,最大值是16万元.
【点睛】本题考查的是正比例函数的性质,一元二次方程的解法,列二次函数的解析式,二次函数的性质,理解题意,选择合适的方法解题是关键.
23.(1)当一次性销售800千克时利润为16000元;
(2)一次性销售量在之间时的最大利润为22500元;
(3)当一次性销售为1300或1700千克时利润为22100元.
【分析】(1)用销售量×利润计算即可;
(2)根据一次性销售不低于1000千克时,每增加1千克降价元求出销售单价,再乘以销售量即可列出函数解析式,再根据函数的性质求最值;
(3)根据(2)中解析式,令y=22100,解方程即可.
【详解】(1)解:根据题意,
当时,,
∴当一次性销售800千克时利润为16000元;
(2)解:设一次性销售量在之间时,
销售价格为,
∴
,
∵,,
∴当时,y有最大值,最大值为22500,
∴一次性销售量在之间时的最大利润为22500元;
(3)解:由(2)知,当时,
,
∴当一次性销售量在之间时,利润为22100元,
∴,
解得,
∴当一次性销售为1300或1700千克时利润为22100元.
【点睛】本题考查二次函数的应用,根据等量关系列出函数解析式,掌握二次函数的性质是解答本题的关键.
24.(1)
(2)点的坐标为
(3)
【分析】(1)设抛物线的解析式为,将,代入即可求解;
(2)点B关于y轴的对称点,则,求出直线与y轴的交点坐标即可;
(3)分和两种情况,根据最小值大于等于9列不等式,即可求解.
【详解】(1)解:抛物线的对称轴与y轴重合,
设抛物线的解析式为,
,,
,,
将,代入,得:
,
解得,
抛物线的解析式为;
(2)解: 抛物线的解析式为,点到对称轴的距离是1,
当时,,
,
作点B关于y轴的对称点,
则,,
,
当,,A共线时,拉杆长度之和最短,
设直线的解析式为,
将,代入,得,
解得,
直线的解析式为,
当时,,
点的坐标为,位置如下图所示:
(3)解:中,
抛物线开口向下,
当时,
在范围内,当时,y取最小值,最小值为:
则,
解得,
;
当时,
在范围内,当时,y取最小值,最小值为:
则,
解得,
;
综上可知,或,
的取值范围为.
【点睛】本题考查二次函数的实际应用,涉及求二次函数解析式,求一次函数解析式,根据对称性求线段的最值,抛物线的增减性等知识点,解题的关键是熟练掌握二次函数的图象和性质,第3问注意分情况讨论.
答案第1页,共2页
答案第1页,共2页
(2023·四川南充·统考中考真题)
1.某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件.已知A产品成本价m元/件(m为常数,且,售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式
(1)若产销A,B两种产品的日利润分别为元,元,请分别写出,与x的函数关系式,并写出x的取值范围;
(2)分别求出产销A,B两种产品的最大日利润.(A产品的最大日利润用含m的代数式表示)
(3)为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.【利润(售价成本)产销数量专利费】
(2023·浙江温州·统考中考真题)
2.一次足球训练中,小明从球门正前方的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为时,球达到最高点,此时球离地面.已知球门高为2.44m,现以O为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素).
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方2.25m处?
(2023·湖北黄冈·统考中考真题)
3.加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元/.
(1)当___________时,元/;
(2)设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?
(3)学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降,乙种蔬菜种植成本平均每年下降,当a为何值时,2025年的总种植成本为元?
(2023·湖北武汉·统考中考真题)
4.某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离(单位:)以、飞行高度(单位:)随飞行时间(单位:)变化的数据如下表.
飞行时间 0 2 4 6 8 …
飞行水平距离 0 10 20 30 40 …
飞行高度 0 22 40 54 64 …
探究发现:与,与之间的数量关系可以用我们已学过的函数来描述.直接写出关于的函数解析式和关于的函数解析式(不要求写出自变量的取值范围).
问题解决:如图,活动小组在水平安全线上处设置一个高度可以变化的发射平台试飞该航模飞机.根据上面的探究发现解决下列问题.
(1)若发射平台相对于安全线的高度为0m,求飞机落到安全线时飞行的水平距离;
(2)在安全线上设置回收区域.若飞机落到内(不包括端点),求发射平台相对于安全线的高度的变化范围.
(2023·山东·统考中考真题)
5.城建部门计划修建一条喷泉步行通道.图1是项目俯视示意图.步行通道的一侧是一排垂直于路面的柱形喷水装置,另一侧是方形水池.图2是主视示意图.喷水装置的高度是2米,水流从喷头A处喷出后呈抛物线路径落入水池内,当水流在与喷头水平距离为2米时达到最高点B,此时距路面的最大高度为3.6米.为避免溅起的水雾影响通道上的行人,计划安装一个透明的倾斜防水罩,防水罩的一端固定在喷水装置上的点处,另一端与路面的垂直高度为1.8米,且与喷泉水流的水平距离为0.3米.点到水池外壁的水平距离米,求步行通道的宽.(结果精确到0.1米)参考数据:
(2023·江苏徐州·统考中考真题)
6.如图,正方形纸片的边长为4,将它剪去4个全等的直角三角形,得到四边形.设的长为,四边形的面积为.
(1)求关于的函数表达式;
(2)当取何值时,四边形的面积为10?
(3)四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
(2023·江苏无锡·统考中考真题)
7.某景区旅游商店以元的价格采购一款旅游食品加工后出售,销售价格不低于元,不高于元,经市场调查发现每天的销售量与销售价格(元)之间的函数关系如图所示.
(1)求关于的函数表达式:
(2)当销售价格定为多少时,该商店销售这款食品每天获得的销售利润最大?最大销售利润是多少?【销售利润=(销售价格一采购价格)×销售量】
(2023·辽宁·统考中考真题)
8.商店出售某品牌护眼灯,每台进价为40元,在销售过程中发现,月销量(台)与销售单价(元)之间满足一次函数关系,规定销售单价不低于进价,且不高于进价的2倍,其部分对应数据如下表所示:
销售单价(元) … 50 60 70 …
月销量(台) … 90 80 70 …
(1)求y与x之间的函数关系式;
(2)当护眼灯销售单价定为多少元时,商店每月出售这种护眼灯所获的利润最大?最大月利润为多少元?
(2023·内蒙古·统考中考真题)
9.随着科技的发展,扫地机器人已广泛应用于生活中,某公司推出一款新型扫地机器人,经统计该产品2022年每个月的销售情况发现,每台的销售价格随销售月份的变化而变化、设该产品2022年第(为整数)个月每台的销售价格为(单位:元),与的函数关系如图所示(图中为一折线).
(1)当时,求每台的销售价格与之间的函数关系式;
(2)设该产品2022年第个月的销售数量为(单位:万台),m与的关系可以用来描述,求哪个月的销售收入最多,最多为多少万元?(销售收入每台的销售价格销售数量)
(2023·湖北·统考中考真题)
10.某商店销售某种商品的进价为每件30元,这种商品在近60天中的日销售价与日销售量的相关信息如下表:
时间:第x(天)
日销售价(元/件) 50
日销售量(件)
(,x为整数)
设该商品的日销售利润为w元.
(1)直接写出w与x的函数关系式__________________;
(2)该商品在第几天的日销售利润最大?最大日销售利润是多少?
(2023·甘肃兰州·统考中考真题)
11.一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离的长.
(2023·山东·统考中考真题)
12.某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为A,B两块(如图所示),花园里种满牡丹和芍药,学校已定购篱笆120米.
(1)设计一个使花园面积最大的方案,并求出其最大面积;
(2)在花园面积最大的条件下,A,B两块内分别种植牡丹和芍药,每平方米种植2株,知牡丹每株售价25元,芍药每株售价15元,学校计划购买费用不超过5万元,求最多可以购买多少株牡丹?
(2023·河南·统考中考真题)
13.小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.
如图,在平面直角坐标系中,点A,C在x轴上,球网与y轴的水平距离,,击球点P在y轴上.若选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系;若选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系.
(1)求点P的坐标和a的值.
(2)小林分析发现,上面两种击球方式均能使球过网.要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式.
(2023·湖北随州·统考中考真题)
14.为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为,已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元
(1)___________, ___________;
(2)求第x天的销售额W元与x之间的函数关系式;
(3)在试销售的30天中,销售额超过1000元的共有多少天?
(2023·河北·统考中考真题)
15.嘉嘉和淇淇在玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.
如图,在平面直角坐标系中,一个单位长度代表1m长.嘉嘉在点处将沙包(看成点)抛出,并运动路线为抛物线的一部分,淇淇恰在点处接住,然后跳起将沙包回传,其运动路线为抛物线的一部分.
(1)写出的最高点坐标,并求a,c的值;
(2)若嘉嘉在x轴上方的高度上,且到点A水平距离不超过的范围内可以接到沙包,求符合条件的n的整数值.
(2023·湖北十堰·统考中考真题)
16.“端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为p盒.
(1)当时,__________;
(2)当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?
(3)小强说:“当日销售利润最大时,日销售额不是最大,”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为.”你认为他们的说法正确吗?若正确,请说明理由;若不正确,请直接写出正确的结论.
(2023·辽宁·统考中考真题)
17.电商平台销售某款儿童组装玩具,进价为每件100元,在销售过程中发现,每周的销售量y(件)与每件玩具售价x(元)之间满足一次函数关系(其中,且x为整数).当每件玩具售价为120元时,每周的销量为80件;当每件玩具售价为140元时,每周的销量为40件.
(1)求y与x之间的函数关系式;
(2)当每件玩具售价为多少元时,电商平台每周销售这款玩具所获的利润最大?最大周利润是多少元?
(2023·江苏宿迁·统考中考真题)
18.某商场销售两种商品,每件进价均为20元.调查发现,如果售出种20件,种10件,销售总额为840元;如果售出种10件,种15件,销售总额为660元.
(1)求两种商品的销售单价.
(2)经市场调研,种商品按原售价销售,可售出40件,原售价每降价1元,销售量可增加10件;种商品的售价不变,种商品售价不低于种商品售价.设种商品降价元,如果两种商品销售量相同,求取何值时,商场销售两种商品可获得总利润最大?最大利润是多少?
(2023·黑龙江大庆·统考中考真题)
19.某建筑物的窗户如图所示,上半部分是等腰三角形,,,点、、分别是边、、的中点;下半部分四边形是矩形,,制造窗户框的材料总长为16米(图中所有黑线的长度和),设米,米.
(1)求与之间的函数关系式,并求出自变量的取值范围;
(2)当为多少时,窗户透过的光线最多(窗户的面积最大),并计算窗户的最大面积.
(2023·山东潍坊·统考中考真题)
20.工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量,,与之间的距离为2米,米,米,,.,,是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?
(2023·辽宁营口·统考中考真题)
21.某大型超市购进一款热销的消毒洗衣液,由于原材料价格上涨,今年每瓶洗衣液的进价比去年每瓶洗衣液的进价上涨4元,今年用1440元购进这款洗衣液的数量与去年用1200元购进这款洗衣液的数量相同.当每瓶洗衣液的现售价为36元时,每周可卖出600瓶,为了能薄利多销.该超市决定降价销售,经市场调查发现,这种洗衣液的售价每降价1元,每周的销量可增加100瓶,规定这种消毒洗衣液每瓶的售价不低于进价.
(1)求今年这款消毒洗衣液每瓶进价是多少元;
(2)当这款消毒洗衣液每瓶的售价定为多少元时,这款洗衣液每周的销售利润最大?最大利润是多少元?
(2023·湖南益阳·统考中考真题)
22.某企业准备对A,B两个生产性项目进行投资,根据其生产成本、销售情况等因素进行分析得知:投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:,投资B项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:.
(1)若将10万元资金投入A项目,一年后获得的收益是多少?
(2)若对A,B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,则m的值是多少?
(3)2023年,我国对小微企业施行所得税优惠政策.该企业将根据此政策获得的减免税款及其他结余资金共计32万元,全部投入到A,B两个项目中,当A,B两个项目分别投入多少万元时,一年后获得的收益之和最大?最大值是多少万元?
(2023·江苏泰州·统考中考真题)
23.某公司的化工产品成本为30元/千克.销售部门规定:一次性销售1000千克以内时,以50元/千克的价格销售;一次性销售不低于1000千克时,每增加1千克降价元.考虑到降价对利润的影响,一次性销售不低于1750千克时,均以某一固定价格销售.一次性销售利润y(元)与一次性销售量x(千克)的函数关系如图所示.
(1)当一次性销售800千克时利润为多少元?
(2)求一次性销售量在之间时的最大利润;
(3)当一次性销售多少千克时利润为22100元?
(2023·贵州·统考中考真题)
24.如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在处,对称轴与水平线垂直,,点在抛物线上,且点到对称轴的距离,点在抛物线上,点到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在上找一点,加装拉杆,同时使拉杆的长度之和最短,请你帮小星找到点的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为,当时,函数的值总大于等于9.求的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1),
(2)元,
(3)当时,该工厂应该选择产销A产品能获得最大日利润;当时,该工厂应该选择产销任一产品都能获得最大日利润;当时,该工厂应该选择产销B产品能获得最大日利润,理由见解析
【分析】(1)根据题木所给的利润计算公式求解即可;
(2)根据(1)所求利用一次函数和二次函数的性质求解即可;
(3)比较(2)中所求A、B两种产品的最大利润即可得到答案.
【详解】(1)解:由题意得,,
(2)解:∵,
∴,
∴随x增大而增大,
∴当时,最大,最大为元;
,
∵,
∴当时,随x增大而增大,
∴当时,最大,最大为元;
(3)解:当,即时,该工厂应该选择产销A产品能获得最大日利润;
当,即时,该工厂应该选择产销任一产品都能获得最大日利润;
当,即时,该工厂应该选择产销B产品能获得最大日利润;
综上所述,当时,该工厂应该选择产销A产品能获得最大日利润;当时,该工厂应该选择产销任一产品都能获得最大日利润;当时,该工厂应该选择产销B产品能获得最大日利润.
【点睛】本题主要考查了一次函数的实际应用,二次函数的实际应用,一元一次不等式的实际应用,正确理解题意列出对应的函数关系式是解题的关键.
2.(1),球不能射进球门
(2)当时他应该带球向正后方移动1米射门
【分析】(1)根据建立的平面直角三角坐标系设抛物线解析式为顶点式,代入A点坐标求出a的值即可得到函数表达式,再把代入函数解析式,求出函数值,与球门高度比较即可得到结论;
(2)根据二次函数平移的规律,设出平移后的解析式,然后将点代入即可求解.
【详解】(1)解:由题意得:抛物线的顶点坐标为,
设抛物线解析式为,
把点代入,得,
解得,
∴抛物线的函数表达式为,
当时,,
∴球不能射进球门;
(2)设小明带球向正后方移动米,则移动后的抛物线为,
把点代入得,
解得(舍去),,
∴当时他应该带球向正后方移动1米射门.
【点睛】此题考查了二次函数的应用,待定系数法求函数解析式、二次函数图象的平移等知识,读懂题意,熟练掌握待定系数法是解题的关键.
3.(1)
(2)当甲种蔬菜的种植面积为,乙种蔬菜的种植面积为时,W最小;
(3)当a为时,2025年的总种植成本为元.
【分析】(1)求出当时,设甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系式为,当时,,求出当时的x的值即可;
(2)当时,,由二次函数性质得到当时,有最小值,最小值为,当时,由一次函数性质得到当时,有最小值,最小值为,比较后即可得到方案;
(3)根据2025年的总种植成本为元列出一元二次方程,解方程即可得到答案.
【详解】(1)解:当时,设甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系式为,把点代入得,
,
解得,
∴当时,,
当时,,
∴当时,,解得,
即当时,元/;
故答案为:;
(2)解:当时,,
∵,
∴抛物线开口向上,
∴当时,有最小值,最小值为,
当时,,
∵,
∴随着x的增大而减小,
∴当时,有最小值,最小值为,
综上可知,当甲种蔬菜的种植面积为,乙种蔬菜的种植面积为时,W最小;
(3)由题意可得,
解得(不合题意,舍去),
∴当a为时,2025年的总种植成本为元.
【点睛】此题考查了二次函数的应用、一元二次方程的应用、一次函数的应用等知识,读懂题意,正确列出函数解析式和方程是解题的关键.
4.探索发现:;问题解决:(1);(2)大于且小于
【分析】探究发现:根据待定系数法求解即可;
问题解决:(1)令二次函数代入函数解析式即可求解;
(2)设发射平台相对于安全线的高度为,则飞机相对于安全线的飞行高度.结合,即可求解.
【详解】探究发现:x与t是一次函数关系,y与t是二次函数关系,
设,,
由题意得:,,
解得:,
∴.
问题解决(1) 解:依题总,得.
解得,(舍),,
当时,.
答:飞机落到安全线时飞行的水平距离为.
(2)解:设发射平台相对于安全线的高度为,飞机相对于安全线的飞行高度.
,
,
,
在中,
当时,;
当时,.
.
答:发射平台相对于安全线的高度的变化范围是大于且小于.
【点睛】本题考查了一次函数与二次函数的应用,利用待定系数法求函数的解析式,关键是把实际问题分析转变成数学模型.
5.3.2米
【分析】先以点O为坐标原点,所在直线为x轴,所在直线为y轴,建立平面直角坐标系,则,,设设抛物线的解析式为,把代入,求得,即,再求出点D的坐标,即可求解.
【详解】解:如图,建立平面直角坐标系,
由题意知:,,
∵抛物线的最高点B,
∴设抛物线的解析式为,
把代入,得,
解得,
∴抛物线的解析式为,
令,则,
解得:,
∴,
∴ (米),
答:步行通道的宽的长约为3.2米.
【点睛】本题考查抛物线的实际应用.熟练掌握用待定系数法求抛物线解析式和抛物线的图象性质是解题的关键.
6.(1)
(2)当取1或3时,四边形的面积为10;
(3)存在,最小值为8.
【分析】(1)先证出四边形为正方形,用未知数x表示其任一边长,根据正方形面积公式即可解决问题;
(2)代入y值,解一元二次方程即可;
(3)把二次函数配方化为顶点式,结合其性质即可求出最小值.
【详解】(1)解:在正方形纸片上剪去4个全等的直角三角形,
,
,四边形为正方形,
在中,,
,
正方形的面积;
不能为负,
,
故关于的函数表达式为
(2)解:令,得,
整理,得,
解得,
故当取1或3时,四边形的面积为10;
(3)解:存在.
正方形的面积;
当时,y有最小值8,即四边形的面积最小为8.
【点睛】本题考查二次函数的应用.解题的关键是找准数量关系,对于第三问,只需把二次函数表达式配方化为顶点式,即可求解.
7.(1)
(2)销售价格为元时,利润最大为
【分析】(1)分时,当时,分别待定系数法求解析式即可求解;
(2)设利润为,根据题意当时,得出,当时,,
进而根据分时,当时,分别求得最大值,即可求解.
【详解】(1)当时,设关于的函数表达式为,将点代入得,
∴
解得:
∴,
当时,设关于的函数表达式为,将点代入得,
解得:
∴,
(2)设利润为
当时,
∵在范围内,随着的增大而增大,
当时,取得最大值为;
当时,
∴当时,w取得最大值为
,
当销售价格为元时,利润最大为.
【点睛】本题考查了一次函数的应用,二次函数的应用,根据题意列出函数关系式是解题的关键.
8.(1)
(2)护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获的利润最大,最大月利润为2400元
【分析】(1)用待定系数法求解即可;
(2)设销售利润为W元,列出W关于x的函数关系式,即可求得最大利润.
【详解】(1)解:由题意设,
由表知,当时,;当时,;
以上值代入函数解析式中得:,
解得:,
所以y与x之间的函数关系式为;
(2)解:设销售利润为W元,
则,
整理得:,
由于销售单价不低于进价,且不高于进价的2倍,则,
∵,,
∴当时,W随x的增大而增大,
∴当时,W有最大值,且最大值为2400;
答:当护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获的利润最大,最大月利润为2400元.
9.(1)
(2)第5个月的销售收入最多,最多为3375万元
【分析】(1)利用待定系数法即可求解;
(2)根据销售收入每台的销售价格销售数量求得销售收入为万元与销售月份之间的函数关系,再利用函数的性质即可求解.
【详解】(1)解:当时,设每台的销售价格与之间的函数关系式为.
∵图象过两点,
,解得
∴当时,每台的销售价格与之间的函数关系式为.
(2)设销售收入为万元,
①当时,,
,当时,(万元).
②当时,,
,
∴随的增大而增大,
∴当时,(万元).
,∴第5个月的销售收入最多,最多为3375万元.
【点睛】本题考查了待定系数法求一次函数的解析式、二次函数在销售问题中的应用,理清题中的数量关系并熟练掌握二次函数的性质是解题的关键.
10.(1)
(2)该商品在第26天的日销售利润最大,最大日销售利润是1296元
【分析】(1)根据利润=单个利润×数量可进行求解;
(2)由(1)分别求出两种情况下的最大利润,然后问题可求解.
【详解】(1)解:由题意得:
当时,则;
当时,则;
∴;
(2)解:当时,;
∵抛物线开口向下,对称轴为直线,
∴当时,(元).
当时,,随增大而减小,
∴当时,(元).
∵,
∴该商品在第26天的日销售利润最大,最大日销售利润是1296元.
【点睛】本题主要考查二次函数与一次函数的应用,熟练掌握一次函数与二次函数的性质是解题的关键.
11.(1)y关于x的函数表达式为;
(2)运动员从起跳点到入水点的水平距离的长为.
【分析】(1)由题意得抛物线的对称轴为,经过点,,利用待定系数法即可求解;
(2)令,解方程即可求解.
【详解】(1)解:由题意得抛物线的对称轴为,经过点,,
设抛物线的表达式为,
∴,解得,
∴y关于x的函数表达式为;
(2)解:令,则,
解得(负值舍去),
∴运动员从起跳点到入水点的水平距离的长为.
【点睛】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握运用待定系数法求抛物线的解析式是解题的关键.
12.(1)长为60米,宽为20米时,有最大面积,且最大面积为1200平方米
(2)最多可以购买1400株牡丹
【分析】(1)设长为x米,面积为y平方米,则宽为米,可以得到y与x的函数关系式,配成顶点式求出函数的最大值即可;
(2)设种植牡丹的面积为a平方米,则种植芍药的面积为平方米,由题意列出不等式求得种植牡丹面积的最大值,即可解答.
【详解】(1)解:设长为x米,面积为y平方米,则宽为米,
∴,
∴当时,y有最大值是1200,
此时,宽为(米)
答:长为60米,宽为20米时,有最大面积,且最大面积为1200平方米.
(2)解:设种植牡丹的面积为a平方米,则种植芍药的面积为平方米,
由题意可得
解得:,
即牡丹最多种植700平方米,
(株),
答:最多可以购买1400株牡丹.
【点睛】本题考查二次函数的应用、一元一次不等式的应用,解题的关键是明确题意,找出所求问题需要的条件.
13.(1),,
(2)选择吊球,使球的落地点到C点的距离更近
【分析】(1)在一次函数上,令,可求得,再代入即可求得的值;
(2)由题意可知,令,分别求得,,即可求得落地点到点的距离,即可判断谁更近.
【详解】(1)解:在一次函数,
令时,,
∴,
将代入中,可得:,
解得:;
(2)∵,,
∴,
选择扣球,则令,即:,解得:,
即:落地点距离点距离为,
∴落地点到C点的距离为,
选择吊球,则令,即:,解得:(负值舍去),
即:落地点距离点距离为,
∴落地点到C点的距离为,
∵,
∴选择吊球,使球的落地点到C点的距离更近.
【点睛】本题考查二次函数与一次函数的应用,理解题意,求得函数解析式是解决问题的关键.
14.(1),
(2)时,,当时,
(3)7天
【分析】(1)利用待定系数法求待定系数;
(2)根据“销售额=售价×销售量”列出函数关系式,
(3)利用二次函数和一次函数的性质分析求解.
【详解】(1)解:∵第5天售价为50元/千克,第10天售价为40元/千克,
∴,解得,
故答案为:,;
(2)解:由题意当时,,
当时,,
(3)解:由题意当时,,
∵,
∴当时,最大为,
当时,,
由时,解得,
又∵x为整数,且,
∴当时,随的增大而增大,
∴第至天,销售额超过1000元,共7天.
【点睛】本题考查一次函数的应用,二次函数的应用,理解题意,分段分析函数解析式,掌握一次函数和二次函数的性质是解题关键.
15.(1)的最高点坐标为,,;
(2)符合条件的n的整数值为4和5.
【分析】(1)利用顶点式即可得到最高点坐标;点在抛物线上,利用待定系数法即可求得a的值;令,即可求得c的值;
(2)求得点A的坐标范围为,求得n的取值范围,即可求解.
【详解】(1)解:∵抛物线,
∴的最高点坐标为,
∵点在抛物线上,
∴,解得:,
∴抛物线的解析式为,令,则;
(2)解:∵到点A水平距离不超过的范围内可以接到沙包,
∴点A的坐标范围为,
当经过时,,
解得;
当经过时,,
解得;
∴
∴符合条件的n的整数值为4和5.
【点睛】本题考查了二次函数的应用,联系实际,读懂题意,熟练掌握二次函数图象上点的坐标特征是解题的关键.
16.(1)
(2)当每盒售价定为65元时,日销售利润W(元)最大,最大利润是元.
(3)他们的说法正确,理由见解析
【分析】(1)根据每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,列式计算即可;
(2)根据销售量乘以每盒的利润得到,根据二次函数的性质即可得到答案;
(3)设日销售额为元,则,根据二次函数的性质即可判断当日销售利润最大时,日销售额不是最大,即可判断小强的说法;当时,由,解得,由抛物线开口向下,得到当时,,即可判断小红的说法.
【详解】(1)解:当时,(盒),
故答案为:
(2)由题意得,
,
又∵,即,
解得,
∵,
∴当时,W最大,最大值为,
∴当每盒售价定为65元时,日销售利润W(元)最大,最大利润是元.
(3)他们的说法正确,理由如下:
设日销售额为元,则
,
∵,
∴当时,最大,最大值为,
∴当时,最大,此时为,
即小强的说法正确;
当时,,解得,
∵抛物线开口向下,
∴当时,∵,
∴当日销售利润不低于元时,每盒售价x的范围为.
故小红的说法错误.
【点睛】此题考查了二次函数的应用,根据题意正确列出函数解析式是基础,熟练掌握二次函数的性质和正确计算是解题的关键.
17.(1)(其中,且x为整数)
(2)当每件玩具售价为130元时,电商平台每周销售这款玩具所获的利润最大,最大周利润是1800元
【分析】(1)设y与x之间的函数关系式为,利用待定系数法求解即可;
(2)设每周销售这款玩具所获的利润为W,列出W关于x的二次函数关系式,化为顶点式即可求解.
【详解】(1)解:设y与x之间的函数关系式为,
由已知得,
解得,
因此y与x之间的函数关系式为(其中,且x为整数);
(2)解:设每周销售这款玩具所获的利润为W,
由题意得,
,
W关于x的二次函数图象开口向上,
,且x为整数,
当时,W取最大值,最大值为1800,
即当每件玩具售价为130元时,电商平台每周销售这款玩具所获的利润最大,最大周利润是1800元.
【点睛】本题考查一次函数与二次函数的实际应用,列出周利润W关于x的二次函数关系式是解题的关键.
18.(1)的销售单价为元、的销售单价为元
(2)当时,商场销售两种商品可获得总利润最大,最大利润是元.
【分析】(1)设的销售单价为元、的销售单价为元,根据题中售出种20件,种10件,销售总额为840元;售出种10件,种15件,销售总额为660元列方程组求解即可得到答案;
(2)设利润为,根据题意,得到,结合二次函数性质及题中限制条件分析求解即可得到答案.
【详解】(1)解:设的销售单价为元、的销售单价为元,则
,解得,
答:的销售单价为元、的销售单价为元;
(2)解:种商品售价不低于种商品售价,
,解得,即,
设利润为,则
,
,
在时能取到最大值,最大值为,
当时,商场销售两种商品可获得总利润最大,最大利润是元.
【点睛】本题考查二元一次方程组及二次函数解实际应用题,读懂题意,根据等量关系列出方程组,根据函数关系找到函数关系式分析是解决问题的关键.
19.(1)
(2)当时,窗户透过的光线最多(窗户的面积最大),最大面积为.
【分析】(1)由可表示出的长,由,可表示出,,,,,的长,进而可求出与之间的函数关系式;
(2)根据(1)中相关数据列出函数解析式,然后利用函数的性质解答.
【详解】(1)∵四边形是矩形,
∴,
∵,
∴.
∵,是边的中点,
∴,,
∵,
∴,
∴.
∵点、、分别是边、的中点,
∴,
∴,
∴,
∴,
∵,
∴,
∴;
(2)设面积为S,
则
,
∴当时,窗户透过的光线最多(窗户的面积最大),最大面积为.
【点睛】本题考查了一次函数的应用,二次函数的应用,正确列出函数解析式是解答本题的关键.
20.当的长度为米时,矩形铁皮的面积最大,最大面积是平方米
【分析】连接,分别交于点,交于点,先判断出四边形是矩形,从而可得,再判断出四边形和四边形都是矩形,从而可得米,,然后设矩形的面积为平方米,米,则米,米,利用矩形的面积公式可得关于的二次函数,最后利用二次函数的性质求解即可得.
【详解】解:如图,连接,分别交于点,交于点,
,
,
米,
四边形是平行四边形,
又,
四边形是矩形,
,,
,
,
四边形是矩形,
,
四边形和四边形都是矩形,
米,,
和都是等腰直角三角形,
,
,
设矩形的面积为平方米,米,则米,米,
米,
米,
,
又,与之间的距离为2米,米,
,
由二次函数的性质可知,当时,随的增大而增大;当时,随的增大而减小,
则当时,取得最大值,最大值为,
答:当的长度为米时,矩形铁皮的面积最大,最大面积是平方米.
【点睛】本题考查了二次函数的几何应用、矩形的判定与性质等知识点,熟练掌握二次函数的性质是解题关键.
21.(1)今年这款消毒洗衣液每瓶进价是24元;
(2)当这款消毒洗衣液每瓶的售价定为33元时,这款洗衣液每周的销售利润最大,最大利润是8100元.
【分析】(1)设今年这款消毒洗衣液每瓶进价是x元,则去年这款消毒洗衣液每瓶进价是元,根据题意列出分式方程,解方程即可;
(2)设这款消毒洗衣液每瓶的售价定为m元时,这款洗衣液每周的销售利润w最大,根据题意得出:,根据二次函数的性质可得出答案.
【详解】(1)解:设今年这款消毒洗衣液每瓶进价是x元,则去年这款消毒洗衣液每瓶进价是元,
根据题意可得:,
解得:,
经检验:是方程的解,
元,
答:今年这款消毒洗衣液每瓶进价是24元.
(2)解:设这款消毒洗衣液每瓶的售价定为m元时,这款洗衣液每周的销售利润w最大,
根据题意得出:,
整理得:,
根据二次函数的性质得出:当时,利润最大,
最大利润为:,
答:当这款消毒洗衣液每瓶的售价定为33元时,这款洗衣液每周的销售利润最大,最大利润是8100元.
【点睛】本题考查分式方程的应用,二次函数的应用,正确理解题意列出关系式是解题关键.
22.(1)4万元
(2)
(3)当A,B两个项目分别投入28万,4万元时,一年后获得的收益之和最大,最大值是16万元.
【分析】(1)把代入可得答案;
(2)当时,可得,再解方程可得答案;
(3)设投入到B项目的资金为万元,则投入到A项目的资金为万元,设总收益为y万元,,而,再利用二次函数的性质可得答案.
【详解】(1)解:∵投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:,
当时,(万元);
(2)∵对A,B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,
∴,
整理得:,
解得:,(不符合题意),
∴m的值为8.
(3)
设投入到B项目的资金为万元,则投入到A项目的资金为万元,设总收益为y万元,
∴
,
而,
∴当时,(万元);
∴当A,B两个项目分别投入28万,4万元时,一年后获得的收益之和最大,最大值是16万元.
【点睛】本题考查的是正比例函数的性质,一元二次方程的解法,列二次函数的解析式,二次函数的性质,理解题意,选择合适的方法解题是关键.
23.(1)当一次性销售800千克时利润为16000元;
(2)一次性销售量在之间时的最大利润为22500元;
(3)当一次性销售为1300或1700千克时利润为22100元.
【分析】(1)用销售量×利润计算即可;
(2)根据一次性销售不低于1000千克时,每增加1千克降价元求出销售单价,再乘以销售量即可列出函数解析式,再根据函数的性质求最值;
(3)根据(2)中解析式,令y=22100,解方程即可.
【详解】(1)解:根据题意,
当时,,
∴当一次性销售800千克时利润为16000元;
(2)解:设一次性销售量在之间时,
销售价格为,
∴
,
∵,,
∴当时,y有最大值,最大值为22500,
∴一次性销售量在之间时的最大利润为22500元;
(3)解:由(2)知,当时,
,
∴当一次性销售量在之间时,利润为22100元,
∴,
解得,
∴当一次性销售为1300或1700千克时利润为22100元.
【点睛】本题考查二次函数的应用,根据等量关系列出函数解析式,掌握二次函数的性质是解答本题的关键.
24.(1)
(2)点的坐标为
(3)
【分析】(1)设抛物线的解析式为,将,代入即可求解;
(2)点B关于y轴的对称点,则,求出直线与y轴的交点坐标即可;
(3)分和两种情况,根据最小值大于等于9列不等式,即可求解.
【详解】(1)解:抛物线的对称轴与y轴重合,
设抛物线的解析式为,
,,
,,
将,代入,得:
,
解得,
抛物线的解析式为;
(2)解: 抛物线的解析式为,点到对称轴的距离是1,
当时,,
,
作点B关于y轴的对称点,
则,,
,
当,,A共线时,拉杆长度之和最短,
设直线的解析式为,
将,代入,得,
解得,
直线的解析式为,
当时,,
点的坐标为,位置如下图所示:
(3)解:中,
抛物线开口向下,
当时,
在范围内,当时,y取最小值,最小值为:
则,
解得,
;
当时,
在范围内,当时,y取最小值,最小值为:
则,
解得,
;
综上可知,或,
的取值范围为.
【点睛】本题考查二次函数的实际应用,涉及求二次函数解析式,求一次函数解析式,根据对称性求线段的最值,抛物线的增减性等知识点,解题的关键是熟练掌握二次函数的图象和性质,第3问注意分情况讨论.
答案第1页,共2页
答案第1页,共2页
同课章节目录
