人教版九年级数学上册22.3实际问题与二次函数 测试卷(无答案)
文档属性
| 名称 | 人教版九年级数学上册22.3实际问题与二次函数 测试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 362.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 09:23:31 | ||
图片预览


文档简介
人教版九年级数学《22.3实际问题与二次函数》测试卷
试卷满分:120分 测试时间:120分钟
选择题(每小题3分,共30分)
1.(2023 东莞市校级模拟)飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数解析式是s=﹣1.5t2+60t,那么飞机着陆后滑行多长时间才能停下来( )
A.10s B.20s C.30s D.40s
2.(2023秋 姑苏区校级月考)2019年在武汉市举行了军运会.在军运会比赛中,某次羽毛球的运动路线可以看作是抛物线的一部分(如图),其中出球点B离地面O点的距离是1米,球落地点A到O点的距离是( )
A.1米 B.3米 C.4米 D.米
3.(2023秋 赵县月考)一个弹性球从地面竖直向上弹起时的速度为6米/秒,经过t秒时,球距离地面的高度h(米)满足公式h=6t﹣5t2,那么球弹起后又回到地面所花的时间t是( )
A.0.6 B.1 C.1.2 D.2
4.(2023秋 河东区校级月考)如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=﹣0.01(x﹣20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.5米 B.4米 C.2.25米 D.1.25米
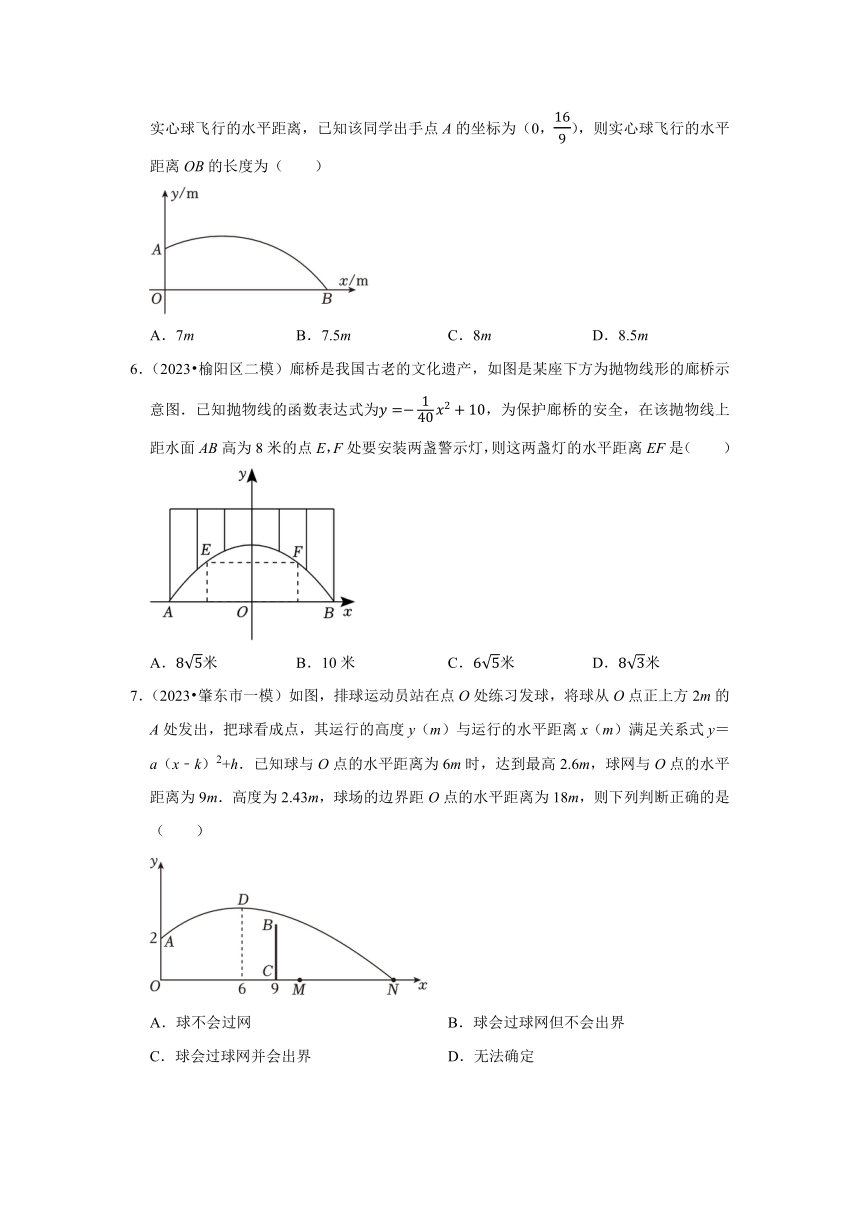
5.(2023秋 东光县月考)小明在期末体育测试中掷出的实心球的运动路线呈抛物线形,若实心球运动的抛物线的解析式为y(x﹣3)2+k,其中y是实心球飞行的高度,x是实心球飞行的水平距离,已知该同学出手点A的坐标为(0,),则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
6.(2023 榆阳区二模)廊桥是我国古老的文化遗产,如图是某座下方为抛物线形的廊桥示意图.已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是( )
A.米 B.10米 C.米 D.米
7.(2023 肇东市一模)如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网 B.球会过球网但不会出界
C.球会过球网并会出界 D.无法确定
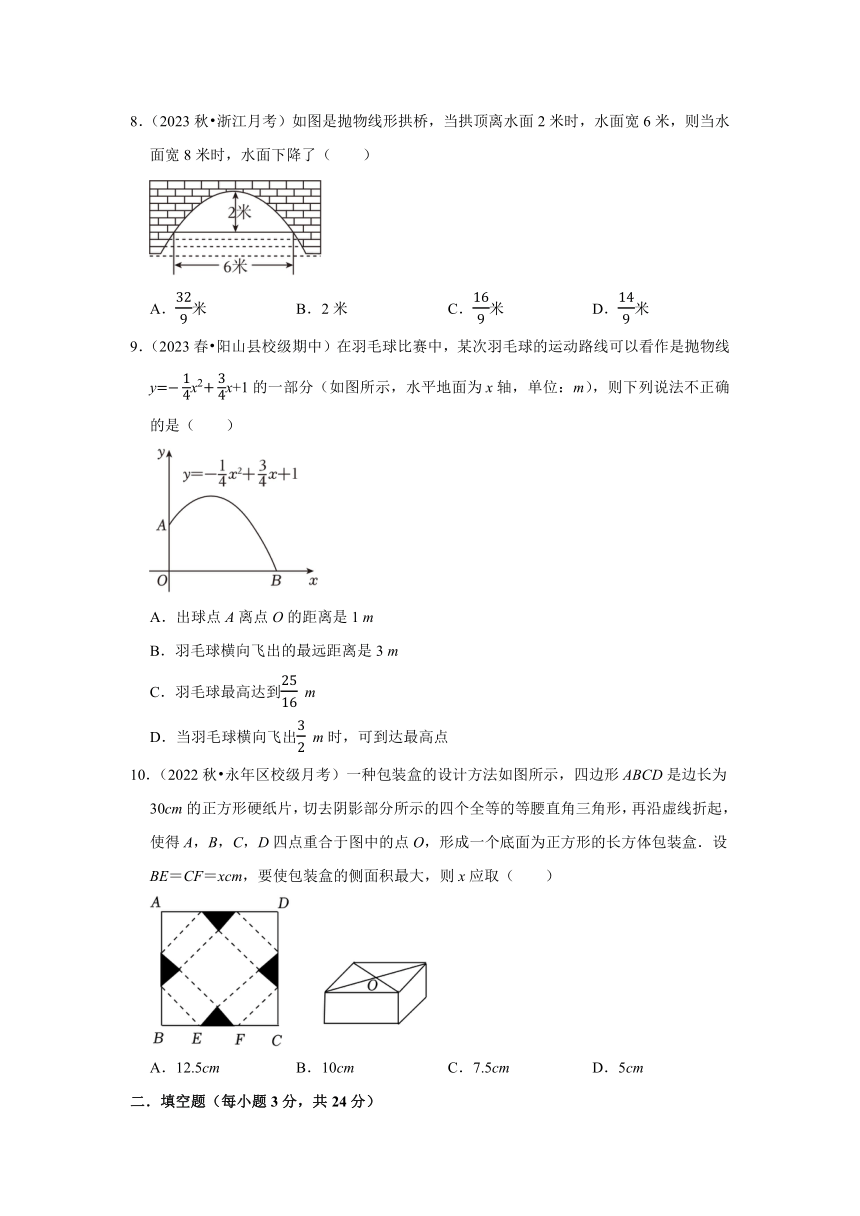
8.(2023秋 浙江月考)如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,则当水面宽8米时,水面下降了( )
A.米 B.2米 C.米 D.米
9.(2023春 阳山县校级期中)在羽毛球比赛中,某次羽毛球的运动路线可以看作是抛物线yx2x+1的一部分(如图所示,水平地面为x轴,单位:m),则下列说法不正确的是( )
A.出球点A离点O的距离是1 m
B.羽毛球横向飞出的最远距离是3 m
C.羽毛球最高达到 m
D.当羽毛球横向飞出 m时,可到达最高点
10.(2022秋 永年区校级月考)一种包装盒的设计方法如图所示,四边形ABCD是边长为30cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒.设BE=CF=xcm,要使包装盒的侧面积最大,则x应取( )
A.12.5cm B.10cm C.7.5cm D.5cm
填空题(每小题3分,共24分)
10.(2023春 罗湖区期中)如图,某小区规划在一块边长为x米的正方形场地上,铺设两条宽为1米的小路,其余部分铺设草坪,则草坪的面积y(米2)与正方形场地边长x(米)之间的关系式为 .
11.(2023 运城模拟)标准大气压下,质量一定的水的体积V(cm3)与温度t(℃)之间的关系满足二次函数(t>0),则当温度为16℃时,水的体积为 cm3.
12.(2022秋 连云港期末)学校航模组设计制作的火箭升空高度n(m)与飞行时间t(s)满足函数表达式h=﹣t2+26t+1.如果火箭在点火升空到最高点时打开降落伞,那么降落伞将在离地面 m处打开.
13.(2023 绿园区校级模拟)要建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3米,水柱落地处离池中心3米,水管长应为 米.
(2023秋 船营区校级月考)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四
周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为,则两个水柱的最高点M,N之间的距离为 m.
15.(2023秋 金乡县月考)某西瓜经营户以2元/千克的价格购进一批西瓜,以3元/千克售出,每天可售出200千克,经调查,售价每降0.1元,每天多卖40千克,另外,每天的其它固定成本24元.当定价为 元能获得最大利润.
16.(2023 阳城县一模)晋阳高速扩建工程作为省市重点项目,是全省第一条“四改八”高速公路,也是全省在建十四条高速公路的品质示范和绿色示范项目.牛王山隧道是晋阳高速的一处路段,如图,隧道的横截面为抛物线形的隧道,底部宽14m,高7m,隧道内双车道通行,交通部门规定车辆必须在中心线两侧行驶,在隧道内禁止变道,且距离道路边缘2m的范围内行驶,并保持车辆顶部与隧道有不少于m的空隙,则通过隧道车辆的限高(最大高度)是 m.
15.(2023 南关区校级模拟)如图,同学们在操场上玩跳大绳游戏,绳甩到最高处时的形状是抛物线型,摇绳的甲、乙两名同学拿绳的手的间距为6米,到地面的距离AO与BD均为0.9米,绳子甩到最高点C处时,最高点距地面的垂直距离为1.8米.身高为1.4米的小吉站在距点O水平距离为m米处,若他能够正常跳大绳(绳子甩到最高时超过他的头顶),则m的取值范围是 .
16.(2023 韩城市二模)如图,已知OP、OQ为两条定长的线段,,OQ=10,∠O=45°,点A、C分别为线段OQ,OP上的点(点C可与点P重合),AB⊥OQ、BC∥OQ,若AB+BC=8,则四边形OABC面积的最大值为 .
三.解答题(共66分)
17.(6分)(2023秋 浑源县月考)如图,这是一位篮球运动员投篮的进球路线,球沿抛物线y=ax2+x+c运动,然后准确落入篮筐内.已知投篮运动员在投篮处A到地面的距离AO=2.25米.以O为坐标原点,建立直角坐标系,篮筐的中心D的坐标为(4,3.05),对称轴与抛物线交于点B,与x轴交于点C.
(1)求抛物线的表达式.
(2)求点B到DH所在直线的距离及点B到地面的距离BC.
18.(7分)(2023秋 虎丘区校级月考)某游乐场的圆形喷水池中心O有一喷水管OA,从点A向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系(单位长度为1m),点A在y轴上,水柱所在的抛物线(第一象限部分)的函数表达式为.
(1)求喷水管高OA.
(2)身高为1.7m的小明站在距离喷水管4m的地方,他会被水喷到吗?
19.(8分)(2023 碑林区一模)如图1,是抛物线形的拱桥,当拱顶高离水面2米时,水面宽4米.如图建立平面直角坐标系,解答下列问题:
(1)如图2,求该抛物线的函数解析式.
(2)当水面AB下降1米,到CD处时,水面宽度增加多少米?(保留根号)
(3)当水面AB上升1米时,水面宽度减少多少米?(保留根号)
20.(8分)(2023秋 汉阳区校级月考)网络销售已经成为一种热门的销售方式,为了减少农产品的库存,某市市长亲自在网络平台上进行直播销售板栗,为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足关系式:y=﹣100x+5000.经销售发现,销售单价不低于成本价且不高于30元/kg.设板栗公司销售该板栗的日获利为w(元).
(1)请求出日获利w与销售单价x之间的函数关系式;
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
21.(9分)(2023秋 呼和浩特月考)如图,用长为45m的篱笆,一面利用墙(墙的最大可用长度是20m),围成中间有一道篱笆的矩形花圃,设花圃的一边长AB是x(单位:m),面积是S(单位:m2).
(1)求S与x的函数关系式及x的取值范围;
(2)如果要围成面积为162m2的花圃,AB的长为多少米?
(3)AB长为多少时,花圃面积最大,最大面积是多少?
22.(9分)(2023 兴宁区校级开学)任意球是足球比赛的主要得分手段之一,在某次足球比赛中,李强站在点O处发出任意球,如图,把球看作点,其运行轨迹的高度y(米)与水平距离x(米)满足函数关系式y=a(x﹣12)2+h,李强罚任意球时防守队员站在李强前方8米处组成人墙,防守队员的身高为2米,对手球门与李强的水平距离为18米,已知足球球门的高是2.43米.
(1)当h=3时,求y与x的函数关系式;
(2)在第(1)问的前提下,足球能否越过人墙?足球能否直接射进球门?请分别说明理由;
(3)若李强罚出任意球一定能直接射进球门得分,直接写出h的取值范围.
23.(9分)(2023秋 启东市校级月考)小颖大学毕业后回家乡创业,开了一家服装专卖店代理某品牌服装的销售.该服装初始售价为每件100元,小颖统计开业10个月以来该服装的每件售价y(元)与月份x的函数关系如图所示,该服装每件的进价z(元)与月份x的关系为.
(1)①求y与x之间的函数关系式;
②第3个月每件服装的利润是多少?
(2)若小颖每个月购进该服装120件,当月销售完毕,第几个月能获得最大利润?最大利润是多少?
24.(10分)(2023 朝阳一模)某水果店销售一种水果,该水果的进价为40元/千克,经市场调查发现:该商品的周销售量y(千克)是售价x(元/千克)的一次函数,部分数据如表:
售价x(元/千克) 45 60 70 75
周销售量y(千克) 110 80 60 50
(1)求出y与x之间的函数表达式;
(2)当售价定为多少元/千克时,每周可获得最大利润?最大利润是多少元?
(3)由于某种原因,该商店进价提高了m元/千克(m>0).通过销售记录发现,当售价大于76元/千克时,每周的利润随售价的增大而减小,请求出m的取值范围.
试卷满分:120分 测试时间:120分钟
选择题(每小题3分,共30分)
1.(2023 东莞市校级模拟)飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数解析式是s=﹣1.5t2+60t,那么飞机着陆后滑行多长时间才能停下来( )
A.10s B.20s C.30s D.40s
2.(2023秋 姑苏区校级月考)2019年在武汉市举行了军运会.在军运会比赛中,某次羽毛球的运动路线可以看作是抛物线的一部分(如图),其中出球点B离地面O点的距离是1米,球落地点A到O点的距离是( )
A.1米 B.3米 C.4米 D.米
3.(2023秋 赵县月考)一个弹性球从地面竖直向上弹起时的速度为6米/秒,经过t秒时,球距离地面的高度h(米)满足公式h=6t﹣5t2,那么球弹起后又回到地面所花的时间t是( )
A.0.6 B.1 C.1.2 D.2
4.(2023秋 河东区校级月考)如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=﹣0.01(x﹣20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.5米 B.4米 C.2.25米 D.1.25米
5.(2023秋 东光县月考)小明在期末体育测试中掷出的实心球的运动路线呈抛物线形,若实心球运动的抛物线的解析式为y(x﹣3)2+k,其中y是实心球飞行的高度,x是实心球飞行的水平距离,已知该同学出手点A的坐标为(0,),则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
6.(2023 榆阳区二模)廊桥是我国古老的文化遗产,如图是某座下方为抛物线形的廊桥示意图.已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是( )
A.米 B.10米 C.米 D.米
7.(2023 肇东市一模)如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网 B.球会过球网但不会出界
C.球会过球网并会出界 D.无法确定
8.(2023秋 浙江月考)如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,则当水面宽8米时,水面下降了( )
A.米 B.2米 C.米 D.米
9.(2023春 阳山县校级期中)在羽毛球比赛中,某次羽毛球的运动路线可以看作是抛物线yx2x+1的一部分(如图所示,水平地面为x轴,单位:m),则下列说法不正确的是( )
A.出球点A离点O的距离是1 m
B.羽毛球横向飞出的最远距离是3 m
C.羽毛球最高达到 m
D.当羽毛球横向飞出 m时,可到达最高点
10.(2022秋 永年区校级月考)一种包装盒的设计方法如图所示,四边形ABCD是边长为30cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒.设BE=CF=xcm,要使包装盒的侧面积最大,则x应取( )
A.12.5cm B.10cm C.7.5cm D.5cm
填空题(每小题3分,共24分)
10.(2023春 罗湖区期中)如图,某小区规划在一块边长为x米的正方形场地上,铺设两条宽为1米的小路,其余部分铺设草坪,则草坪的面积y(米2)与正方形场地边长x(米)之间的关系式为 .
11.(2023 运城模拟)标准大气压下,质量一定的水的体积V(cm3)与温度t(℃)之间的关系满足二次函数(t>0),则当温度为16℃时,水的体积为 cm3.
12.(2022秋 连云港期末)学校航模组设计制作的火箭升空高度n(m)与飞行时间t(s)满足函数表达式h=﹣t2+26t+1.如果火箭在点火升空到最高点时打开降落伞,那么降落伞将在离地面 m处打开.
13.(2023 绿园区校级模拟)要建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3米,水柱落地处离池中心3米,水管长应为 米.
(2023秋 船营区校级月考)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四
周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为,则两个水柱的最高点M,N之间的距离为 m.
15.(2023秋 金乡县月考)某西瓜经营户以2元/千克的价格购进一批西瓜,以3元/千克售出,每天可售出200千克,经调查,售价每降0.1元,每天多卖40千克,另外,每天的其它固定成本24元.当定价为 元能获得最大利润.
16.(2023 阳城县一模)晋阳高速扩建工程作为省市重点项目,是全省第一条“四改八”高速公路,也是全省在建十四条高速公路的品质示范和绿色示范项目.牛王山隧道是晋阳高速的一处路段,如图,隧道的横截面为抛物线形的隧道,底部宽14m,高7m,隧道内双车道通行,交通部门规定车辆必须在中心线两侧行驶,在隧道内禁止变道,且距离道路边缘2m的范围内行驶,并保持车辆顶部与隧道有不少于m的空隙,则通过隧道车辆的限高(最大高度)是 m.
15.(2023 南关区校级模拟)如图,同学们在操场上玩跳大绳游戏,绳甩到最高处时的形状是抛物线型,摇绳的甲、乙两名同学拿绳的手的间距为6米,到地面的距离AO与BD均为0.9米,绳子甩到最高点C处时,最高点距地面的垂直距离为1.8米.身高为1.4米的小吉站在距点O水平距离为m米处,若他能够正常跳大绳(绳子甩到最高时超过他的头顶),则m的取值范围是 .
16.(2023 韩城市二模)如图,已知OP、OQ为两条定长的线段,,OQ=10,∠O=45°,点A、C分别为线段OQ,OP上的点(点C可与点P重合),AB⊥OQ、BC∥OQ,若AB+BC=8,则四边形OABC面积的最大值为 .
三.解答题(共66分)
17.(6分)(2023秋 浑源县月考)如图,这是一位篮球运动员投篮的进球路线,球沿抛物线y=ax2+x+c运动,然后准确落入篮筐内.已知投篮运动员在投篮处A到地面的距离AO=2.25米.以O为坐标原点,建立直角坐标系,篮筐的中心D的坐标为(4,3.05),对称轴与抛物线交于点B,与x轴交于点C.
(1)求抛物线的表达式.
(2)求点B到DH所在直线的距离及点B到地面的距离BC.
18.(7分)(2023秋 虎丘区校级月考)某游乐场的圆形喷水池中心O有一喷水管OA,从点A向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系(单位长度为1m),点A在y轴上,水柱所在的抛物线(第一象限部分)的函数表达式为.
(1)求喷水管高OA.
(2)身高为1.7m的小明站在距离喷水管4m的地方,他会被水喷到吗?
19.(8分)(2023 碑林区一模)如图1,是抛物线形的拱桥,当拱顶高离水面2米时,水面宽4米.如图建立平面直角坐标系,解答下列问题:
(1)如图2,求该抛物线的函数解析式.
(2)当水面AB下降1米,到CD处时,水面宽度增加多少米?(保留根号)
(3)当水面AB上升1米时,水面宽度减少多少米?(保留根号)
20.(8分)(2023秋 汉阳区校级月考)网络销售已经成为一种热门的销售方式,为了减少农产品的库存,某市市长亲自在网络平台上进行直播销售板栗,为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足关系式:y=﹣100x+5000.经销售发现,销售单价不低于成本价且不高于30元/kg.设板栗公司销售该板栗的日获利为w(元).
(1)请求出日获利w与销售单价x之间的函数关系式;
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
21.(9分)(2023秋 呼和浩特月考)如图,用长为45m的篱笆,一面利用墙(墙的最大可用长度是20m),围成中间有一道篱笆的矩形花圃,设花圃的一边长AB是x(单位:m),面积是S(单位:m2).
(1)求S与x的函数关系式及x的取值范围;
(2)如果要围成面积为162m2的花圃,AB的长为多少米?
(3)AB长为多少时,花圃面积最大,最大面积是多少?
22.(9分)(2023 兴宁区校级开学)任意球是足球比赛的主要得分手段之一,在某次足球比赛中,李强站在点O处发出任意球,如图,把球看作点,其运行轨迹的高度y(米)与水平距离x(米)满足函数关系式y=a(x﹣12)2+h,李强罚任意球时防守队员站在李强前方8米处组成人墙,防守队员的身高为2米,对手球门与李强的水平距离为18米,已知足球球门的高是2.43米.
(1)当h=3时,求y与x的函数关系式;
(2)在第(1)问的前提下,足球能否越过人墙?足球能否直接射进球门?请分别说明理由;
(3)若李强罚出任意球一定能直接射进球门得分,直接写出h的取值范围.
23.(9分)(2023秋 启东市校级月考)小颖大学毕业后回家乡创业,开了一家服装专卖店代理某品牌服装的销售.该服装初始售价为每件100元,小颖统计开业10个月以来该服装的每件售价y(元)与月份x的函数关系如图所示,该服装每件的进价z(元)与月份x的关系为.
(1)①求y与x之间的函数关系式;
②第3个月每件服装的利润是多少?
(2)若小颖每个月购进该服装120件,当月销售完毕,第几个月能获得最大利润?最大利润是多少?
24.(10分)(2023 朝阳一模)某水果店销售一种水果,该水果的进价为40元/千克,经市场调查发现:该商品的周销售量y(千克)是售价x(元/千克)的一次函数,部分数据如表:
售价x(元/千克) 45 60 70 75
周销售量y(千克) 110 80 60 50
(1)求出y与x之间的函数表达式;
(2)当售价定为多少元/千克时,每周可获得最大利润?最大利润是多少元?
(3)由于某种原因,该商店进价提高了m元/千克(m>0).通过销售记录发现,当售价大于76元/千克时,每周的利润随售价的增大而减小,请求出m的取值范围.
同课章节目录
