数学人教A版(2019)必修第一册第三章函数的概念与性质单元复习(共38张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册第三章函数的概念与性质单元复习(共38张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 06:56:08 | ||
图片预览










文档简介
(共38张PPT)
必修第一册 第三章
函数的概念与性质
章末复习
第三章 函数的概念与性质
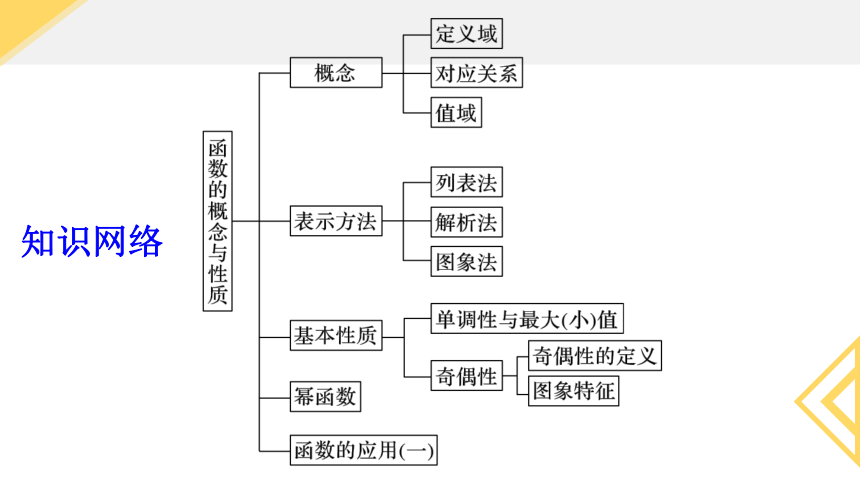
知识网络
知识点梳理
1.函数的概念
一般地,设A,B是非空的 ,如果对于集合A中的 一个数x,按照某种确定的对应关系f,在集合B中都有 的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A.
2.函数的三要素
(1)函数的三要素: 、 、 .
(2)如果两个函数的 相同,并且 完全一致,则这两个函数为同一个函数.
实数集
任意
唯一确定
定义域
对应关系
值域
定义域
对应关系
知识点梳理
3.函数的表示法
表示函数的常用方法有 、图象法和 .
4.分段函数
若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,这种函数称为分段函数.
解析法
列表法
知识点梳理
增函数 减函数
定义 一般地,设函数f(x)的定义域为I,区间D I,如果 x1,x2∈D 当x15.函数的单调性
(1)单调函数的定义
f(x1)f(x1)>f(x2)
图象描述 自左向右看图象是上升的
自左向右看图象是下降的
知识点梳理
(2)单调区间的定义
如果函数y=f(x)在区间D上_________或_________,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
单调递增
单调递减
前提 设函数y=f(x)的定义域为I,如果存在实数M满足 条件 (1) x∈I,都有________; (2) x0∈I,使得_________ (1) x∈I,都有_________;
(2) x0∈I,使得_________
结论 M为最大值 M为最小值
6.函数的最值
f(x)≤M
f(x)≥M
f(x0)=M
f(x0)=M
知识点梳理
奇偶性 定义 图象特点
偶函数 一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,且___________,那么函数f(x)就叫做偶函数 关于____对称
奇函数 一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,且_____________,那么函数f(x)就叫做奇函数 关于_____对称
7.函数的奇偶性
f(-x)=f(x)
y轴
f(-x)=-f(x)
原点
知识点梳理
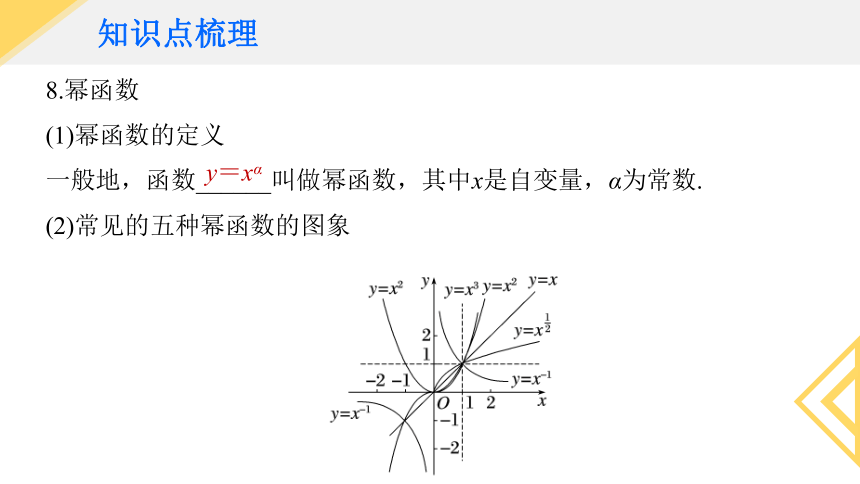
8.幂函数
(1)幂函数的定义
一般地,函数______叫做幂函数,其中x是自变量,α为常数.
(2)常见的五种幂函数的图象
y=xα
知识点梳理
(3)幂函数的性质
①幂函数在(0,+∞)上都有定义;
②当α>0时,幂函数的图象都过点_____和_____,且在(0,+∞)上单调递增;
③当α<0时,幂函数的图象都过点_____,且在(0,+∞)上单调递减;
④当α为奇数时,y=xα为_______;当α为偶数时,y=xα为_______.
(1,1)
(0,0)
(1,1)
奇函数
偶函数
知识点梳理
一次函数
二次函数
幂函数型
分段函数
常见函数模型
9.常见函数模型
【例1】函数的定义域为 .
【答案】
【解析】函数有意义,
则,解得或,
所以函数的定义域为.
故答案为:
题型一:求具体函数与抽象函数的定义域
【对点训练1】若函数的定义域为,则函数的定义域是 .
【答案】
【解析】函数的定义域为,
于是有,
即函数的定义域,
故答案为:
题型一:求具体函数与抽象函数的定义域
【对点训练2】已知函数的定义域为,则函数的定义域为 .
【答案】
【解析】由题意得,解得,
所以的定义域为,
故答案为:
题型一:求具体函数与抽象函数的定义域
【对点训练3】已知函数的定义域为,则函数的定义域为 .
【答案】
【解析】因为,即,
所以,所以,
所以.
故答案为:.
题型一:求具体函数与抽象函数的定义域
【例2】(1)已知为二次函数,且 ,求函数的解析式;
(2)已知,求函数 的解析式.
【解析】(1)设 ,
则有:
,
所以 , 所以 ,
所以 .
(2) 令 .
则 ,
所以 ,
所以 的解析式为 .
题型二:求函数的解析式
【对点训练4】(1)已知是二次函数,且满足,,求解析式;
(2)已知,求的解析式.
(3)若对任意实数x,均有,求的解析式.
【解析】(1)令 ,
因为,所以,
则.
由题意可知:
,
得,所以.
所以.
(2)令,则,
.
.
(3)因为①,
所以②,
由①②得:,
解得:.
题型二:求函数的解析式
【对点训练5】(1)已知,求的解析式;
(2)已知,求函数的解析式;
(3)已知是二次函数,且满足,,求函数的解析式;
(4)已知,求的解析式.
(5)已知是定义在R上的函数,,且对任意的实数x,y都有,求函数的解析式.
【解析】(1).
(2) 设,则,,
即,
所以,
所以.
(3)因为是二次函数,所以设.由,得c=1.
由,得
,
整理得,
所以,所以,
所以.
(4)用-x替换中的x,
得,
由,
解得.
(5)令,
则,
所以.
题型二:求函数的解析式
【例3】求下列函数的值域.
(1);
(2);
(3).
【解析】(1)由于,且;
所以可得,
因此函数的值域是.
(2)令,所以,
即,
当时,,
即函数的值域为.
(3)易知需满足,即,
即函数定义域为;
,
由二次函数性质可得,
所以的值域为.
题型三:求函数的值域
【对点训练6】求下列函数的值域:
(1), (2),
(3), (4)
【解析】(1)由题意可得:,
因为,则,
所以原函数的值域为.
(2)因为,
则,当且仅当,
即时,等号成立,
所以原函数的值域为.
(3)令,解得,
可得函数的定义域为,
因为,
可得
所以原函数的值域为.
(4)设,则,
所以原函数转化为,
因为函数的图象开口向下,对称轴方程为,
可知当时,函数取到最大值,
所以原函数的值域为.
题型三:求函数的值域
【例4】(2023·山东·高一山东省实验中学校考阶段练习)函数的单调递增区间为 .
【答案】
【解析】由题意可得,
即,解得:,
所以函数的定义域是,
是由和 复合而成,
因为对称轴为,开口向下,
所以在区间上单调递增,在区间上单调递减,
而单调递增,
所以的单调递增区间是,
故答案为:.
题型四:函数的单调性
【对点训练7】(2023·黑龙江齐齐哈尔·高一校联考期中)函数在R上单调递减,则实数a的取值范围是 .
【答案】
【解析】当时,
,根据其是由函数向右平移1个单位再向上平移1个单位得到,
则在上单调递减,
由题意得,解得,则的取值范围为.
题型四:函数的单调性
【对点训练8】(2023·湖北武汉·高一校联考期中)函数是定义在上的增函数,若对于任意正实数,恒有,且,则不等式的解集是 .
【答案】
【解析】,,
,
则不等式等价为
,
函数在定义域上为增函数,
不等式等价为,
即,解得,
不等式的解集为
题型四:函数的单调性
【对点训练9】(2023·河北邯郸·高一校考期末)已知定义在上的函数满足:①对任意的,都有;②当且仅当时,成立.
(1)求;
(2)用定义证明的单调性;
【解析】(1)令,则由题意可得
,
(2)任取且,即,
由题意可得
,
而当且仅当时,,
所以,即,
所以函数在单调递减.
题型四:函数的单调性
【对点训练10】(2023·天津·高一统考期中)已知函数是奇函数,且.
(1)求的解析式;
(2)判断在区间上的单调性并说明理由.
【解析】(1)因为函数是奇函数,
所以,即,
因为不恒为0,所以,
所以,
因为,所以,
所以,所以,
所以的解析式为.
(2)在区间上的单调递减.
证明:任取且,只需证明.
易知,
所以
,
因为,所以,
所以,
所以,所以,
因为,所以,
所以,
所以,即,
所以在区间上的单调递减.
题型四:函数的单调性
【例5】(2023·全国·高一期中)已知函数,且.
(1)求实数的值;
(2)判断该函数的奇偶性;
(3)判断函数在上的单调性,并证明.
【解析】(1),且,
,
;
(2)由(1)得函数,
定义域为关于原点对称
,
函数为奇函数.
(3)函数在上是增函数,
任取,,不妨设,
则
,
且
,,
,即,
在上是增函数.
题型五:函数的奇偶性
【对点训练11】(2023·全国·高一期中)已知定义在,,上的函数满足:①,,,,;②当时,,且.
(1)试判断函数的奇偶性;
(2)判断函数在上的单调性;
(3)求函数在区间,,上的最大值;
(4)求不等式的解集.
【解析】(1)令,则,
得;
再令,则,
得.
对于条件,令,
则,所以.
又函数的定义域关于原点对称,所以函数为偶函数.
(2)任取,,且,则有.
又当时,,
而,
所以函数在上是增函数.
(3).
又由(1)知函数在区间,,上是偶函数且在上是增函数,
函数在区间,,上的最大值为
(4),
,
原不等式等价于
又函数为偶函数,且函数在上是增函数,
原不等式又等价于,
即或,
不等式的解集为或
题型五:函数的奇偶性
【对点训练12】(2023·江西南昌·高一南昌市八一中学校考阶段练习)已知函数是定义在上的奇函数,当时,,其中
(1)求函数的解析式;
(2)若函数在区间不单调,求出实数的取值范围.
【解析】(1)由是定义在上的奇函数,
所以,
又时,,
所以时,,
所以,
所以函数的解析式为.
(2)当时,,
若,由知,在上递增,不合题意;
,,
所以在上先减再增,符合函数在上不单调,
综上,实数的取值范围为.
题型五:函数的奇偶性
【例6】(多选题)(2023·黑龙江齐齐哈尔·高一校联考期中)函数,,用表示,中的较大者,记为,则下列说法正确的是( )
A. B., C.有最大值 D.最小值为0
【答案】BD
【解析】令,即,
解得或,
所以可知
,
所以,故A错误;
当时,,故B正确;
由(或)可知,函数无最大值,故C错误;
当或时,,当时,,
所以最小值为0,故D正确.
故选:BD
题型六:函数性质的综合应用
【对点训练13】(多选题)(2023·福建福州·高一校联考期中)已知连续函数对任意实数恒有,当时,,,则( )
A. B.在上的最大值是4
C.图像关于中心对称 D.不等式的解集为
【答案】ACD
【解析】令,
则,即A正确;
令,则,
又,∴,
,
则
,
即C正确;
由,即B项错误;
由条件可得
,
当时,,
即在定义域上单调递增,
,
即,即D正确;
故选:ACD
题型六:函数性质的综合应用
【对点训练14】(2023·全国·高一期中)已知函数
(1)设在区间的最小值为,求的表达式;
(2)设,若函数在区间上是增函数,求实数a的取值范围.
【解析】(1)由于,当时,
对称轴为,
当即时,在上为增函数,
;
当即时,;
当即时,在上为减函数,
综上可得.
(2),
在区间上任取,
则
(*)
∵在上为增函数,
∴
∴(*)可转化为对任意,在区间上都成立.
即
因为,
所以,
由
得,
解得;
所以实数a的取值范围是.
题型六:函数性质的综合应用
【例7】(2023·浙江金华·高一校考期中)已知点在幂函数的图像上.
(1)求的解析式;
(2)若函数,是否存在实数a,使得最小值为5?若存在,求出a的值;若不存在,说明理由
【解析】(1)设幂函数,
由点在幂函数的图象上,
所以,
解得,
所以.
(2)函数,,且二次函数的图象是抛物线,对称轴是.
①当,即时,在上是单调增函数,最小值为,解得,满足题意;
②当,即时,在上先减后增,最小值为,方程无解;
综上知,存在实数,使得有最小值为.
题型七:幂函数
【对点训练15】(2023·全国·高一假期作业)已知幂函数的图象关于y轴对称,且在上单调递增.
(1)求m和n的值;
(2)求满足不等式的a的取值范围.
【解析】(1)∵是幂函数,
∴,解得m=3.
由在上单调递增得,
解得.
∵,
∴或.
当时,函数,图象关于y轴对称,符合题意.
当时,函数,图象关于原点对称,不合题意.
综上,,.
(2)由(1)得,,
∴.
∵函数在和上均单调递减,
∴当时,,
当时,.
∴满足不等式的条件为或或,
解得或,
∴满足不等式的的取值范围.
题型七:幂函数
【对点训练16】(2023·广西柳州·高一柳铁一中校联考阶段练习)已知幂函数,
且.
(1)求函数的解析式;
(2)试判断是否存在正数,使得函数在区间上的最大值为5,若存在,求出的值,若不存在,请说明理由.
【解析】(1)由题知,,
解得或,
当时,,满足,
当时,,不满足,
所以.
(2).
当时,在区间上单调递增,在上单调递减,
所以,
解得,不合题意;
当时,在区间上递增,
所以,解得.
综上所述,存在正数,使得在区间上的最大值为5.
题型七:幂函数
【例8】某地区去年用电量为,电价为0.8元/,今年计划将电价降到0.55~0.75元/.用户心理承受价位是0.40元/.下调电价后,实际价位和用户心理价位仍存在差距,假设新增的用电量与这个差值成反比(比例系数为0.2a),该地区的电力成本价为0.3元/,那么电价定为多少时仍可保证电力部门的收益增长率不低于20%?
【解析】设下调后的电价为x元,
依题意知,新增用电量与实际电价和用户期望电价的差成反比(比例系数为0.2a),
则新增用电量为,即用电量增至,
所以今年电力部门的收益
;
要保证电力部门的收益增长率不低于20%,
则,
由,
整理得,
解得.
答:当电价定到0.60~0.75元/,仍可保证电力部门的收益比上年至少增长20%.
题型八:函数的实际应用
【对点训练17】某公司每月最多生产100台报警系统装置,生产台的收入函数为(单位:元),其成本函数为(单位:元),利润是收入与成本之差.
(1)求利润函数及利润函数的最大值;
(2)为了促销,如果每月还需投入500元的宣传费用,设每台产品的利润为,求的最大值及此时的值.
【解析】(1)由题意知,
,
易得的对称轴为,
所以当或时,取得最大值为(元).
所以利润函数,最大值为(元);
(2)依题意,得
(元).
当且仅当时等号成立,
即时,等号成立.
所以当台时,每台产品的利润取得最大值元.
题型八:函数的实际应用
【对点训练18】巴拿马运河起着连接美洲南北陆路通道的作用,是世界上最繁忙的运河之一,假设运河上的船只航行速度为(单位:海里/小时),船只的密集度为(单位:艘/海里),当运河上的船只密度为50艘/海里时,河道拥堵,此时航行速度为0;当船只密度不超过5艘/海里时,船只的速度为45海里/小时,数据统计表明:当时,船只的速度是船只密集度的一次函数.
(1)当时,求函数的表达式;
(2)当船只密度为多大时,单位时间内,通过的船只数量可以达到最大值,求出最大值.(取整)
【解析】(1)由题意知
时,海里/小时;
当时,设,
则,解得,
故;
(2)由(1)可得
,
当时,,
此时;
当时,
,
当时,取到最大值为625;
由于,故当船只密度为25艘/海里时,通过的船只数量可以达到最大值,
最大值为625.
题型八:函数的实际应用
好学数学
数学好学
学好数学
必修第一册 第三章
函数的概念与性质
章末复习
第三章 函数的概念与性质
知识网络
知识点梳理
1.函数的概念
一般地,设A,B是非空的 ,如果对于集合A中的 一个数x,按照某种确定的对应关系f,在集合B中都有 的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A.
2.函数的三要素
(1)函数的三要素: 、 、 .
(2)如果两个函数的 相同,并且 完全一致,则这两个函数为同一个函数.
实数集
任意
唯一确定
定义域
对应关系
值域
定义域
对应关系
知识点梳理
3.函数的表示法
表示函数的常用方法有 、图象法和 .
4.分段函数
若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,这种函数称为分段函数.
解析法
列表法
知识点梳理
增函数 减函数
定义 一般地,设函数f(x)的定义域为I,区间D I,如果 x1,x2∈D 当x1
(1)单调函数的定义
f(x1)
图象描述 自左向右看图象是上升的
自左向右看图象是下降的
知识点梳理
(2)单调区间的定义
如果函数y=f(x)在区间D上_________或_________,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
单调递增
单调递减
前提 设函数y=f(x)的定义域为I,如果存在实数M满足 条件 (1) x∈I,都有________; (2) x0∈I,使得_________ (1) x∈I,都有_________;
(2) x0∈I,使得_________
结论 M为最大值 M为最小值
6.函数的最值
f(x)≤M
f(x)≥M
f(x0)=M
f(x0)=M
知识点梳理
奇偶性 定义 图象特点
偶函数 一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,且___________,那么函数f(x)就叫做偶函数 关于____对称
奇函数 一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,且_____________,那么函数f(x)就叫做奇函数 关于_____对称
7.函数的奇偶性
f(-x)=f(x)
y轴
f(-x)=-f(x)
原点
知识点梳理
8.幂函数
(1)幂函数的定义
一般地,函数______叫做幂函数,其中x是自变量,α为常数.
(2)常见的五种幂函数的图象
y=xα
知识点梳理
(3)幂函数的性质
①幂函数在(0,+∞)上都有定义;
②当α>0时,幂函数的图象都过点_____和_____,且在(0,+∞)上单调递增;
③当α<0时,幂函数的图象都过点_____,且在(0,+∞)上单调递减;
④当α为奇数时,y=xα为_______;当α为偶数时,y=xα为_______.
(1,1)
(0,0)
(1,1)
奇函数
偶函数
知识点梳理
一次函数
二次函数
幂函数型
分段函数
常见函数模型
9.常见函数模型
【例1】函数的定义域为 .
【答案】
【解析】函数有意义,
则,解得或,
所以函数的定义域为.
故答案为:
题型一:求具体函数与抽象函数的定义域
【对点训练1】若函数的定义域为,则函数的定义域是 .
【答案】
【解析】函数的定义域为,
于是有,
即函数的定义域,
故答案为:
题型一:求具体函数与抽象函数的定义域
【对点训练2】已知函数的定义域为,则函数的定义域为 .
【答案】
【解析】由题意得,解得,
所以的定义域为,
故答案为:
题型一:求具体函数与抽象函数的定义域
【对点训练3】已知函数的定义域为,则函数的定义域为 .
【答案】
【解析】因为,即,
所以,所以,
所以.
故答案为:.
题型一:求具体函数与抽象函数的定义域
【例2】(1)已知为二次函数,且 ,求函数的解析式;
(2)已知,求函数 的解析式.
【解析】(1)设 ,
则有:
,
所以 , 所以 ,
所以 .
(2) 令 .
则 ,
所以 ,
所以 的解析式为 .
题型二:求函数的解析式
【对点训练4】(1)已知是二次函数,且满足,,求解析式;
(2)已知,求的解析式.
(3)若对任意实数x,均有,求的解析式.
【解析】(1)令 ,
因为,所以,
则.
由题意可知:
,
得,所以.
所以.
(2)令,则,
.
.
(3)因为①,
所以②,
由①②得:,
解得:.
题型二:求函数的解析式
【对点训练5】(1)已知,求的解析式;
(2)已知,求函数的解析式;
(3)已知是二次函数,且满足,,求函数的解析式;
(4)已知,求的解析式.
(5)已知是定义在R上的函数,,且对任意的实数x,y都有,求函数的解析式.
【解析】(1).
(2) 设,则,,
即,
所以,
所以.
(3)因为是二次函数,所以设.由,得c=1.
由,得
,
整理得,
所以,所以,
所以.
(4)用-x替换中的x,
得,
由,
解得.
(5)令,
则,
所以.
题型二:求函数的解析式
【例3】求下列函数的值域.
(1);
(2);
(3).
【解析】(1)由于,且;
所以可得,
因此函数的值域是.
(2)令,所以,
即,
当时,,
即函数的值域为.
(3)易知需满足,即,
即函数定义域为;
,
由二次函数性质可得,
所以的值域为.
题型三:求函数的值域
【对点训练6】求下列函数的值域:
(1), (2),
(3), (4)
【解析】(1)由题意可得:,
因为,则,
所以原函数的值域为.
(2)因为,
则,当且仅当,
即时,等号成立,
所以原函数的值域为.
(3)令,解得,
可得函数的定义域为,
因为,
可得
所以原函数的值域为.
(4)设,则,
所以原函数转化为,
因为函数的图象开口向下,对称轴方程为,
可知当时,函数取到最大值,
所以原函数的值域为.
题型三:求函数的值域
【例4】(2023·山东·高一山东省实验中学校考阶段练习)函数的单调递增区间为 .
【答案】
【解析】由题意可得,
即,解得:,
所以函数的定义域是,
是由和 复合而成,
因为对称轴为,开口向下,
所以在区间上单调递增,在区间上单调递减,
而单调递增,
所以的单调递增区间是,
故答案为:.
题型四:函数的单调性
【对点训练7】(2023·黑龙江齐齐哈尔·高一校联考期中)函数在R上单调递减,则实数a的取值范围是 .
【答案】
【解析】当时,
,根据其是由函数向右平移1个单位再向上平移1个单位得到,
则在上单调递减,
由题意得,解得,则的取值范围为.
题型四:函数的单调性
【对点训练8】(2023·湖北武汉·高一校联考期中)函数是定义在上的增函数,若对于任意正实数,恒有,且,则不等式的解集是 .
【答案】
【解析】,,
,
则不等式等价为
,
函数在定义域上为增函数,
不等式等价为,
即,解得,
不等式的解集为
题型四:函数的单调性
【对点训练9】(2023·河北邯郸·高一校考期末)已知定义在上的函数满足:①对任意的,都有;②当且仅当时,成立.
(1)求;
(2)用定义证明的单调性;
【解析】(1)令,则由题意可得
,
(2)任取且,即,
由题意可得
,
而当且仅当时,,
所以,即,
所以函数在单调递减.
题型四:函数的单调性
【对点训练10】(2023·天津·高一统考期中)已知函数是奇函数,且.
(1)求的解析式;
(2)判断在区间上的单调性并说明理由.
【解析】(1)因为函数是奇函数,
所以,即,
因为不恒为0,所以,
所以,
因为,所以,
所以,所以,
所以的解析式为.
(2)在区间上的单调递减.
证明:任取且,只需证明.
易知,
所以
,
因为,所以,
所以,
所以,所以,
因为,所以,
所以,
所以,即,
所以在区间上的单调递减.
题型四:函数的单调性
【例5】(2023·全国·高一期中)已知函数,且.
(1)求实数的值;
(2)判断该函数的奇偶性;
(3)判断函数在上的单调性,并证明.
【解析】(1),且,
,
;
(2)由(1)得函数,
定义域为关于原点对称
,
函数为奇函数.
(3)函数在上是增函数,
任取,,不妨设,
则
,
且
,,
,即,
在上是增函数.
题型五:函数的奇偶性
【对点训练11】(2023·全国·高一期中)已知定义在,,上的函数满足:①,,,,;②当时,,且.
(1)试判断函数的奇偶性;
(2)判断函数在上的单调性;
(3)求函数在区间,,上的最大值;
(4)求不等式的解集.
【解析】(1)令,则,
得;
再令,则,
得.
对于条件,令,
则,所以.
又函数的定义域关于原点对称,所以函数为偶函数.
(2)任取,,且,则有.
又当时,,
而,
所以函数在上是增函数.
(3).
又由(1)知函数在区间,,上是偶函数且在上是增函数,
函数在区间,,上的最大值为
(4),
,
原不等式等价于
又函数为偶函数,且函数在上是增函数,
原不等式又等价于,
即或,
不等式的解集为或
题型五:函数的奇偶性
【对点训练12】(2023·江西南昌·高一南昌市八一中学校考阶段练习)已知函数是定义在上的奇函数,当时,,其中
(1)求函数的解析式;
(2)若函数在区间不单调,求出实数的取值范围.
【解析】(1)由是定义在上的奇函数,
所以,
又时,,
所以时,,
所以,
所以函数的解析式为.
(2)当时,,
若,由知,在上递增,不合题意;
,,
所以在上先减再增,符合函数在上不单调,
综上,实数的取值范围为.
题型五:函数的奇偶性
【例6】(多选题)(2023·黑龙江齐齐哈尔·高一校联考期中)函数,,用表示,中的较大者,记为,则下列说法正确的是( )
A. B., C.有最大值 D.最小值为0
【答案】BD
【解析】令,即,
解得或,
所以可知
,
所以,故A错误;
当时,,故B正确;
由(或)可知,函数无最大值,故C错误;
当或时,,当时,,
所以最小值为0,故D正确.
故选:BD
题型六:函数性质的综合应用
【对点训练13】(多选题)(2023·福建福州·高一校联考期中)已知连续函数对任意实数恒有,当时,,,则( )
A. B.在上的最大值是4
C.图像关于中心对称 D.不等式的解集为
【答案】ACD
【解析】令,
则,即A正确;
令,则,
又,∴,
,
则
,
即C正确;
由,即B项错误;
由条件可得
,
当时,,
即在定义域上单调递增,
,
即,即D正确;
故选:ACD
题型六:函数性质的综合应用
【对点训练14】(2023·全国·高一期中)已知函数
(1)设在区间的最小值为,求的表达式;
(2)设,若函数在区间上是增函数,求实数a的取值范围.
【解析】(1)由于,当时,
对称轴为,
当即时,在上为增函数,
;
当即时,;
当即时,在上为减函数,
综上可得.
(2),
在区间上任取,
则
(*)
∵在上为增函数,
∴
∴(*)可转化为对任意,在区间上都成立.
即
因为,
所以,
由
得,
解得;
所以实数a的取值范围是.
题型六:函数性质的综合应用
【例7】(2023·浙江金华·高一校考期中)已知点在幂函数的图像上.
(1)求的解析式;
(2)若函数,是否存在实数a,使得最小值为5?若存在,求出a的值;若不存在,说明理由
【解析】(1)设幂函数,
由点在幂函数的图象上,
所以,
解得,
所以.
(2)函数,,且二次函数的图象是抛物线,对称轴是.
①当,即时,在上是单调增函数,最小值为,解得,满足题意;
②当,即时,在上先减后增,最小值为,方程无解;
综上知,存在实数,使得有最小值为.
题型七:幂函数
【对点训练15】(2023·全国·高一假期作业)已知幂函数的图象关于y轴对称,且在上单调递增.
(1)求m和n的值;
(2)求满足不等式的a的取值范围.
【解析】(1)∵是幂函数,
∴,解得m=3.
由在上单调递增得,
解得.
∵,
∴或.
当时,函数,图象关于y轴对称,符合题意.
当时,函数,图象关于原点对称,不合题意.
综上,,.
(2)由(1)得,,
∴.
∵函数在和上均单调递减,
∴当时,,
当时,.
∴满足不等式的条件为或或,
解得或,
∴满足不等式的的取值范围.
题型七:幂函数
【对点训练16】(2023·广西柳州·高一柳铁一中校联考阶段练习)已知幂函数,
且.
(1)求函数的解析式;
(2)试判断是否存在正数,使得函数在区间上的最大值为5,若存在,求出的值,若不存在,请说明理由.
【解析】(1)由题知,,
解得或,
当时,,满足,
当时,,不满足,
所以.
(2).
当时,在区间上单调递增,在上单调递减,
所以,
解得,不合题意;
当时,在区间上递增,
所以,解得.
综上所述,存在正数,使得在区间上的最大值为5.
题型七:幂函数
【例8】某地区去年用电量为,电价为0.8元/,今年计划将电价降到0.55~0.75元/.用户心理承受价位是0.40元/.下调电价后,实际价位和用户心理价位仍存在差距,假设新增的用电量与这个差值成反比(比例系数为0.2a),该地区的电力成本价为0.3元/,那么电价定为多少时仍可保证电力部门的收益增长率不低于20%?
【解析】设下调后的电价为x元,
依题意知,新增用电量与实际电价和用户期望电价的差成反比(比例系数为0.2a),
则新增用电量为,即用电量增至,
所以今年电力部门的收益
;
要保证电力部门的收益增长率不低于20%,
则,
由,
整理得,
解得.
答:当电价定到0.60~0.75元/,仍可保证电力部门的收益比上年至少增长20%.
题型八:函数的实际应用
【对点训练17】某公司每月最多生产100台报警系统装置,生产台的收入函数为(单位:元),其成本函数为(单位:元),利润是收入与成本之差.
(1)求利润函数及利润函数的最大值;
(2)为了促销,如果每月还需投入500元的宣传费用,设每台产品的利润为,求的最大值及此时的值.
【解析】(1)由题意知,
,
易得的对称轴为,
所以当或时,取得最大值为(元).
所以利润函数,最大值为(元);
(2)依题意,得
(元).
当且仅当时等号成立,
即时,等号成立.
所以当台时,每台产品的利润取得最大值元.
题型八:函数的实际应用
【对点训练18】巴拿马运河起着连接美洲南北陆路通道的作用,是世界上最繁忙的运河之一,假设运河上的船只航行速度为(单位:海里/小时),船只的密集度为(单位:艘/海里),当运河上的船只密度为50艘/海里时,河道拥堵,此时航行速度为0;当船只密度不超过5艘/海里时,船只的速度为45海里/小时,数据统计表明:当时,船只的速度是船只密集度的一次函数.
(1)当时,求函数的表达式;
(2)当船只密度为多大时,单位时间内,通过的船只数量可以达到最大值,求出最大值.(取整)
【解析】(1)由题意知
时,海里/小时;
当时,设,
则,解得,
故;
(2)由(1)可得
,
当时,,
此时;
当时,
,
当时,取到最大值为625;
由于,故当船只密度为25艘/海里时,通过的船只数量可以达到最大值,
最大值为625.
题型八:函数的实际应用
好学数学
数学好学
学好数学
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
