勾股定理
图片预览





文档简介
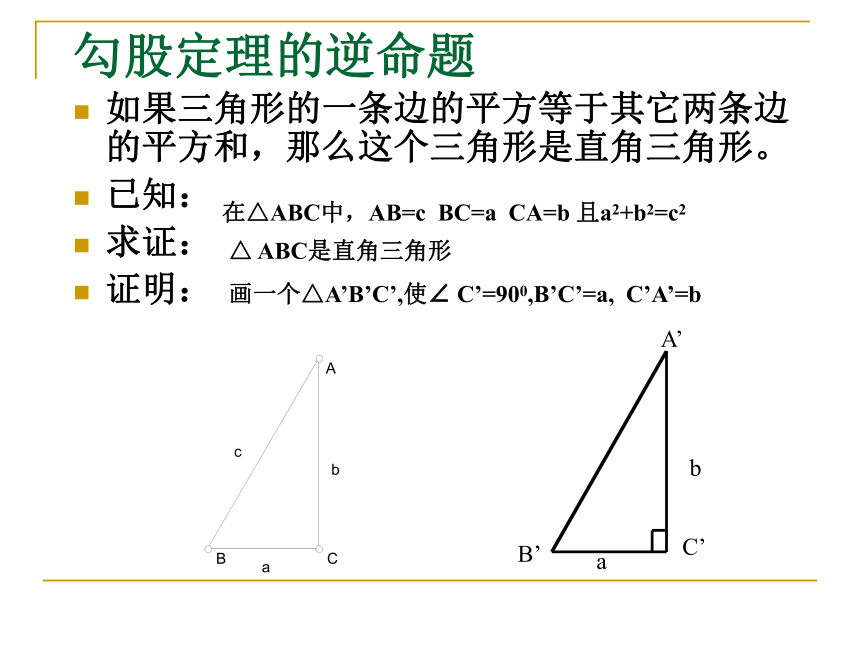
课件17张PPT。课题:勾股定理的逆定理ACB操作每个同学的桌上有一段12cm长的线,请同学量出4cm,用大头钉固定好把生下的线分成5cm和3cm两段拉紧固定,用量角器量出最大角的度数。勾股定理的逆命题如果三角形的一条边的平方等于其它两条边的平方和,那么这个三角形是直角三角形。
已知:
求证:
证明:
在△ABC中,AB=c BC=a CA=b 且a2+b2=c2△ ABC是直角三角形画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=babA’B’C’∵ ∠ C’=900∴ A’B’2= a2+b2∵ a2+b2=c2∴ A’B’ 2=c2∴ A’B’ =c∵ 边长取正值∴ △ ABC ≌△ A’B’C’(SSS)∴ ∠ C= ∠ C’(全等三角形对应角相等)∴ ∠C= 900已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ ABC是直角三角形证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b在△ ABC和△ A’B’C’中∴ △ ABC是直角三角形(直角三角形的定义)如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。勾股定理的逆定理(1)上述结论中,哪条边所对的角是直角?
(2)如果三角形中较短两边的平方和不等于
最长的平方,那么这个三角形是直角三角形吗?想一想:例1.根据下列条件,分别判断以a,b,c
为边的三角形是不是直角三角形?
(1)a=7,b=24,c=25;
(2)a= , b=1,c= .练习一下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ________ ________(3) a=41 b=9 c=40 _______ ________(4) a:b: c=3:4:5 ________ ________是是是是∠ A=900∠ B=900∠ A=900∠ C=900例2 如果△ABC的三边长分别为 a,b,c,且
a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)
则△ABC是直角三角形
解:∵ a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)∴a2+b2=(m2-n2)2+(2mn)2=m4-2m2n2+n4+4m2n2=m4+2m2n2+n4=(m2+n2)2=c2∴△ABC是直角三角形。 课堂练习:
一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( )
2.? ABC的a=6,b=8,则c=10 ( )
二填空题
1.在? ABC中,C=90°,
(1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______.
2.在? ABC中, C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.??例1已知:在△ ABC中, AB=15cm,AC=20cm, BC=25cm,AD是BC边上的中线。求: AD的长。解: ∵ AB=15cm,AC=20cm,BC=25cm∴ AB2+AC2=225+400=625
BC2=625∴ AB2+AC2=BC2∵ ∠ BAC=900(勾股定理的逆定理)已知:在△ ABC中, AB=15cm,AC=20cm,
BC=25cm,AD是BC边上的高。
求: AD的长。练习解: ∵ AB=15cm,AC=20cm,BC=25cm∴ AB2+AC2=225+400=625
BC2=625∴ AB2+AC2=BC2∵ ∠ BAC=900(勾股定理的逆定理)应用拓展:解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25∴AD=4,DF=2,FC=2,EC=1∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF求:(1) S四边形ABCD。例2∵AC⊥AB(已知)∴ AC2+AB2=BC2(勾股定理)∵ AB=3cm,BC=5cm∴ AC2=16 , CD2+AD2=12+4=16∴ AC2=CD2+AD2∴ ∠ADC=900(勾股定理的逆定理∴ S四边形ABCD=S △ ABC+ S△ ACD∴解:解:∵ RtADC中AD=2, AC=4∴ ∠ DCA=300(在直角三角形中如果一条直角边等于斜边的一半,那么这条直角边所对的角等于300)求:(1) S四边形ABCD。(2)∠ DCA的度数例2小结利用勾股定理,已知直角三角形的两条边,可以求出第三边,利用勾股定理的逆定理,可以判定一个角为直角。从而判定直角三角形,也可以用来判定两 直线互相垂直。思考题在平面直角坐标系中有RT △ ABC,已知A(2,4),B(0,-2),点A(2,4),B(0,-2),点C在X轴上,求点C的坐标。
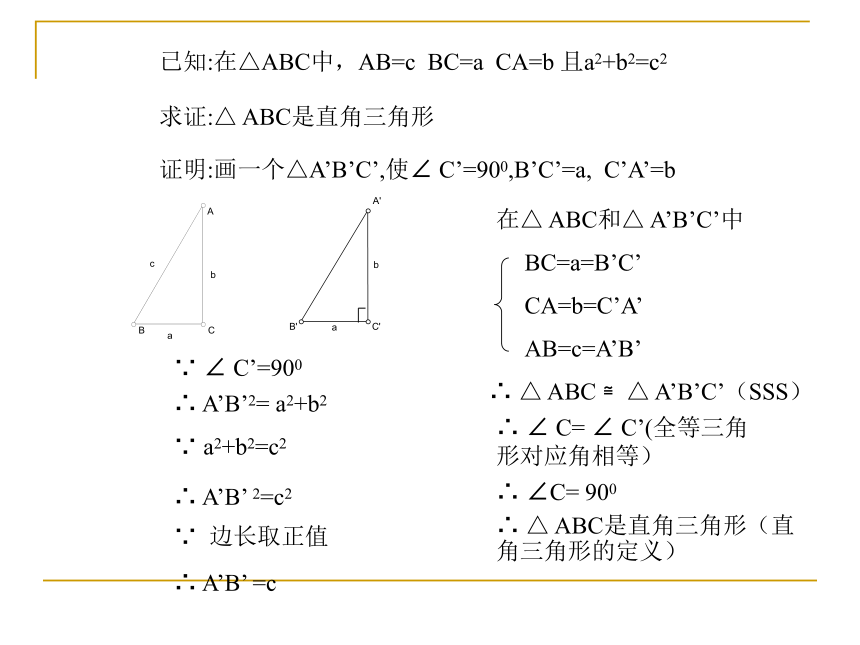
已知:
求证:
证明:
在△ABC中,AB=c BC=a CA=b 且a2+b2=c2△ ABC是直角三角形画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=babA’B’C’∵ ∠ C’=900∴ A’B’2= a2+b2∵ a2+b2=c2∴ A’B’ 2=c2∴ A’B’ =c∵ 边长取正值∴ △ ABC ≌△ A’B’C’(SSS)∴ ∠ C= ∠ C’(全等三角形对应角相等)∴ ∠C= 900已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ ABC是直角三角形证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b在△ ABC和△ A’B’C’中∴ △ ABC是直角三角形(直角三角形的定义)如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。勾股定理的逆定理(1)上述结论中,哪条边所对的角是直角?
(2)如果三角形中较短两边的平方和不等于
最长的平方,那么这个三角形是直角三角形吗?想一想:例1.根据下列条件,分别判断以a,b,c
为边的三角形是不是直角三角形?
(1)a=7,b=24,c=25;
(2)a= , b=1,c= .练习一下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ________ ________(3) a=41 b=9 c=40 _______ ________(4) a:b: c=3:4:5 ________ ________是是是是∠ A=900∠ B=900∠ A=900∠ C=900例2 如果△ABC的三边长分别为 a,b,c,且
a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)
则△ABC是直角三角形
解:∵ a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)∴a2+b2=(m2-n2)2+(2mn)2=m4-2m2n2+n4+4m2n2=m4+2m2n2+n4=(m2+n2)2=c2∴△ABC是直角三角形。 课堂练习:
一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( )
2.? ABC的a=6,b=8,则c=10 ( )
二填空题
1.在? ABC中,C=90°,
(1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______.
2.在? ABC中, C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.??例1已知:在△ ABC中, AB=15cm,AC=20cm, BC=25cm,AD是BC边上的中线。求: AD的长。解: ∵ AB=15cm,AC=20cm,BC=25cm∴ AB2+AC2=225+400=625
BC2=625∴ AB2+AC2=BC2∵ ∠ BAC=900(勾股定理的逆定理)已知:在△ ABC中, AB=15cm,AC=20cm,
BC=25cm,AD是BC边上的高。
求: AD的长。练习解: ∵ AB=15cm,AC=20cm,BC=25cm∴ AB2+AC2=225+400=625
BC2=625∴ AB2+AC2=BC2∵ ∠ BAC=900(勾股定理的逆定理)应用拓展:解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25∴AD=4,DF=2,FC=2,EC=1∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF求:(1) S四边形ABCD。例2∵AC⊥AB(已知)∴ AC2+AB2=BC2(勾股定理)∵ AB=3cm,BC=5cm∴ AC2=16 , CD2+AD2=12+4=16∴ AC2=CD2+AD2∴ ∠ADC=900(勾股定理的逆定理∴ S四边形ABCD=S △ ABC+ S△ ACD∴解:解:∵ RtADC中AD=2, AC=4∴ ∠ DCA=300(在直角三角形中如果一条直角边等于斜边的一半,那么这条直角边所对的角等于300)求:(1) S四边形ABCD。(2)∠ DCA的度数例2小结利用勾股定理,已知直角三角形的两条边,可以求出第三边,利用勾股定理的逆定理,可以判定一个角为直角。从而判定直角三角形,也可以用来判定两 直线互相垂直。思考题在平面直角坐标系中有RT △ ABC,已知A(2,4),B(0,-2),点A(2,4),B(0,-2),点C在X轴上,求点C的坐标。
