3.1.1函数及其表示方法(第一课时) 课件(共20张PPT)
文档属性
| 名称 | 3.1.1函数及其表示方法(第一课时) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 09:31:50 | ||
图片预览








文档简介
(共20张PPT)
3.1.1函数及其表示方法(1)
在数学中函数概念的解释有两个基本的派别,第一派叫古典派,它的主要目标是数学在物理和技术中的传统应用,以“变量”的概念为基础。初中数学里的函数概念属于这一派;第二派叫现代派(或集合论派),以“元素”概念为基础,函数概念的外延更广,用于所有传统的数学应用和新近出现的新的应用领域.这节课我们一起学习一下吧.
1.理解函数的概念,了解构成函数的三要素.(重点、难点)
2.会判断给出的两个函数是否是同一函数.
3.会求一些简单函数的定义域.(重点)
探究点1 函数的概念
思考1:初中我们学习过哪些函数呢?你能举几个例子吗?
【提示】正比例函数,一次函数,
反比例函数,二次函数.
思考2:初中我们学习的函数是怎样定义的?
【提示】在一个变化过程中,数值发生变化的量称为变量;在一个变化过程中,如果有两个变量与,并且对于的每一个确定的值,都有唯一确定的值与其对应,那么就称是的函数.
(1)国家统计局的课题组公布,如果将2005年中国创新指数记为100,近些年来中国创新指数的情况如下表所示。
思考3:观察下列两个实例有什么不同点和共同点?与初中学习的函数是否相同?
以y表示年度值,i表示中国创新指数的取值,则是的的函数吗?如果是,这个函数用数学符号可以怎样表示?
【提示】是的函数.的变化范围是数集{2008,2009,20100,2011,2012,2013,2014,2015},的变化范围是数集{116.5,125.5,131.8,139.6,148.2,152.6,158.2,171.5}.并且对于数集中每一个,按照图表,在数集中都有唯一确定的与之对应.
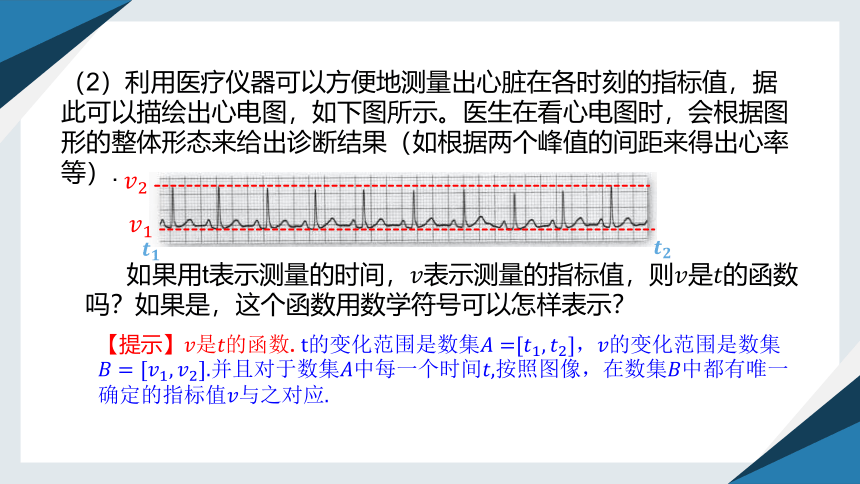
(2)利用医疗仪器可以方便地测量出心脏在各时刻的指标值,据此可以描绘出心电图,如下图所示。医生在看心电图时,会根据图形的整体形态来给出诊断结果(如根据两个峰值的间距来得出心率等).
如果用t表示测量的时间,表示测量的指标值,则是的函数吗?如果是,这个函数用数学符号可以怎样表示?
【提示】是的函数.的变化范围是数集[],的变化范围是数集.并且对于数集中每一个时间,按照图像,在数集中都有唯一确定的指标值与之对应.
两个实例有什么共同点和不同点?
不同点
实例1是用表格刻画变量之间的对应关系.
实例2是用图象刻画变量之间的对应关系.
共同点
(1)都有两个非空数集.
(2)两个数集之间都有一种确定的对应关系.
初中实际上是用变量的观点和解析式来描述函数的,但从这两个实例可知,初中的方法有一定的局限性:实例中的是的函数,是的函数,但是这两个函数与初中的函数有所不同,比如都很难用一个解析式表示,而且每个变量的取值范围也有了限制,等等.
那么如何给函数下一个新的定义呢?
一般地,给定两个非空实数集与,以及对应关系,如果对于集合中的每一个实数,在集合中都有唯一确定的实数与对应,则称为定义在集合上的一个函数,记作
,,
其中称为自变量,称为因变量,自变量取值的范围(即数集)称为这个函数的定义域.
{|,}
称为函数的值域.
函数
所有函数值组成的集合
注意:
2.如何理解“ ”?
【解析】符号表示“ 是变量的函数”,它仅仅是函数符号,并不表示等于与的乘积,是对应关系,也可用其他小写英文字母如 , 等表示.例如:即表示.
【解析】当为常数时,表示的是自变量时对应的函数值,是一个常数,也可以记作 .
1.函数概念中的关键词
【解析】(1) A,B是非空数集.(2)任意的∈A,存在唯一的∈B与之对应.
3.与的区别和联系.
即时训练:
下列可作为函数的图象的是( )
A B C D
x
x
x
x
y
y
y
y
O
O
O
O
√
D
是否一个自变量的值仅对应一个函数值
例1 求下列函数的定义域:
(1) (2)
【解析】(1)因为函数有意义当且仅当
解得,所以函数的定义域为
(2)因为函数有意义当且仅当
解得且,所以函数的定义域为
在表示函数时,如果不会产生歧义,函数的定义域通常省略不写,此时就约定:函数的定义域就是使得这个函数有意义的所有实数组成的集合.
【总结】
1.求函数定义域常用的依据:
(1)分式中分母不能为零;
(2)二次根式中的被开方数要大于或等于零;
(3)零次方的底数不能为零;
(4)实际问题要有意义.
2.定义域要写成集合或区间形式.
跟踪训练 求下列函数的定义域:
【解析】(1)因为函数有意义当且仅当
解得,所以函数的定义域为
(2)因为函数有意义当且仅当
解得,所以函数的定义域为
探究点2 相等函数
思考1:函数与是同一函数吗?
提示:不是,定义域不同
思考3:函数与是同一函数吗?
提示:是,定义域相同,对应关系相同
思考2:函数与是同一函数吗?
提示:是,定义域相同,对应关系
一般地,如果两个函数表达式表示的函数定义域相同,对应关系也相同,则称这两个函数表达式表示的就是同一函数.
即时训练 下列函数是否表示同一函数.
(1);
(2);
(3);
(4).
是
是
不是,定义域不同
不是,定义域不同
例2 设函数的值域为S,分别判断和3是否是S中的元素.
【解析】由于恒成立,所以无解,因此,.
当时,可解得,即,所以.
用方程去判断一个数是否属于函数的值域.
例3 已知:
(1)求和;
(2)求函数的值域.
【解析】(1)由已知可得
(2)(方法一)因为
所以恒成立,从而可知
又因为当的绝对值逐渐变大时,函数值会逐渐接近于0,但不会等于0,
因此所求函数值域为.
观察法
(方法二)假设是所求值域中的元素,则关于的方程应该
有解,即应该有解,从而
解得.因此所求函数值域为.
方程法
求函数的值域,应先确定定义域,遵循定义域优先原则,再根据具体情况求的取值范围.
注意
跟踪训练 求下列函数的值域.
(1);(2)
【解析】(1)
因此,函数的值域为
(2)
因此,函数的值域为
定义域
值域
函数的概念
函数的记法
函数
3.1.1函数及其表示方法(1)
在数学中函数概念的解释有两个基本的派别,第一派叫古典派,它的主要目标是数学在物理和技术中的传统应用,以“变量”的概念为基础。初中数学里的函数概念属于这一派;第二派叫现代派(或集合论派),以“元素”概念为基础,函数概念的外延更广,用于所有传统的数学应用和新近出现的新的应用领域.这节课我们一起学习一下吧.
1.理解函数的概念,了解构成函数的三要素.(重点、难点)
2.会判断给出的两个函数是否是同一函数.
3.会求一些简单函数的定义域.(重点)
探究点1 函数的概念
思考1:初中我们学习过哪些函数呢?你能举几个例子吗?
【提示】正比例函数,一次函数,
反比例函数,二次函数.
思考2:初中我们学习的函数是怎样定义的?
【提示】在一个变化过程中,数值发生变化的量称为变量;在一个变化过程中,如果有两个变量与,并且对于的每一个确定的值,都有唯一确定的值与其对应,那么就称是的函数.
(1)国家统计局的课题组公布,如果将2005年中国创新指数记为100,近些年来中国创新指数的情况如下表所示。
思考3:观察下列两个实例有什么不同点和共同点?与初中学习的函数是否相同?
以y表示年度值,i表示中国创新指数的取值,则是的的函数吗?如果是,这个函数用数学符号可以怎样表示?
【提示】是的函数.的变化范围是数集{2008,2009,20100,2011,2012,2013,2014,2015},的变化范围是数集{116.5,125.5,131.8,139.6,148.2,152.6,158.2,171.5}.并且对于数集中每一个,按照图表,在数集中都有唯一确定的与之对应.
(2)利用医疗仪器可以方便地测量出心脏在各时刻的指标值,据此可以描绘出心电图,如下图所示。医生在看心电图时,会根据图形的整体形态来给出诊断结果(如根据两个峰值的间距来得出心率等).
如果用t表示测量的时间,表示测量的指标值,则是的函数吗?如果是,这个函数用数学符号可以怎样表示?
【提示】是的函数.的变化范围是数集[],的变化范围是数集.并且对于数集中每一个时间,按照图像,在数集中都有唯一确定的指标值与之对应.
两个实例有什么共同点和不同点?
不同点
实例1是用表格刻画变量之间的对应关系.
实例2是用图象刻画变量之间的对应关系.
共同点
(1)都有两个非空数集.
(2)两个数集之间都有一种确定的对应关系.
初中实际上是用变量的观点和解析式来描述函数的,但从这两个实例可知,初中的方法有一定的局限性:实例中的是的函数,是的函数,但是这两个函数与初中的函数有所不同,比如都很难用一个解析式表示,而且每个变量的取值范围也有了限制,等等.
那么如何给函数下一个新的定义呢?
一般地,给定两个非空实数集与,以及对应关系,如果对于集合中的每一个实数,在集合中都有唯一确定的实数与对应,则称为定义在集合上的一个函数,记作
,,
其中称为自变量,称为因变量,自变量取值的范围(即数集)称为这个函数的定义域.
{|,}
称为函数的值域.
函数
所有函数值组成的集合
注意:
2.如何理解“ ”?
【解析】符号表示“ 是变量的函数”,它仅仅是函数符号,并不表示等于与的乘积,是对应关系,也可用其他小写英文字母如 , 等表示.例如:即表示.
【解析】当为常数时,表示的是自变量时对应的函数值,是一个常数,也可以记作 .
1.函数概念中的关键词
【解析】(1) A,B是非空数集.(2)任意的∈A,存在唯一的∈B与之对应.
3.与的区别和联系.
即时训练:
下列可作为函数的图象的是( )
A B C D
x
x
x
x
y
y
y
y
O
O
O
O
√
D
是否一个自变量的值仅对应一个函数值
例1 求下列函数的定义域:
(1) (2)
【解析】(1)因为函数有意义当且仅当
解得,所以函数的定义域为
(2)因为函数有意义当且仅当
解得且,所以函数的定义域为
在表示函数时,如果不会产生歧义,函数的定义域通常省略不写,此时就约定:函数的定义域就是使得这个函数有意义的所有实数组成的集合.
【总结】
1.求函数定义域常用的依据:
(1)分式中分母不能为零;
(2)二次根式中的被开方数要大于或等于零;
(3)零次方的底数不能为零;
(4)实际问题要有意义.
2.定义域要写成集合或区间形式.
跟踪训练 求下列函数的定义域:
【解析】(1)因为函数有意义当且仅当
解得,所以函数的定义域为
(2)因为函数有意义当且仅当
解得,所以函数的定义域为
探究点2 相等函数
思考1:函数与是同一函数吗?
提示:不是,定义域不同
思考3:函数与是同一函数吗?
提示:是,定义域相同,对应关系相同
思考2:函数与是同一函数吗?
提示:是,定义域相同,对应关系
一般地,如果两个函数表达式表示的函数定义域相同,对应关系也相同,则称这两个函数表达式表示的就是同一函数.
即时训练 下列函数是否表示同一函数.
(1);
(2);
(3);
(4).
是
是
不是,定义域不同
不是,定义域不同
例2 设函数的值域为S,分别判断和3是否是S中的元素.
【解析】由于恒成立,所以无解,因此,.
当时,可解得,即,所以.
用方程去判断一个数是否属于函数的值域.
例3 已知:
(1)求和;
(2)求函数的值域.
【解析】(1)由已知可得
(2)(方法一)因为
所以恒成立,从而可知
又因为当的绝对值逐渐变大时,函数值会逐渐接近于0,但不会等于0,
因此所求函数值域为.
观察法
(方法二)假设是所求值域中的元素,则关于的方程应该
有解,即应该有解,从而
解得.因此所求函数值域为.
方程法
求函数的值域,应先确定定义域,遵循定义域优先原则,再根据具体情况求的取值范围.
注意
跟踪训练 求下列函数的值域.
(1);(2)
【解析】(1)
因此,函数的值域为
(2)
因此,函数的值域为
定义域
值域
函数的概念
函数的记法
函数
