2023-2024学年苏科版九年级数学上第七周周末提优训练(圆+5.1)(含答案)
文档属性
| 名称 | 2023-2024学年苏科版九年级数学上第七周周末提优训练(圆+5.1)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 14:21:24 | ||
图片预览




文档简介
2023-2024学年苏科版九年级数学上第七周周末提优训练(圆+5.1)
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共30分)
1.下列事件中,属于必然事件的是( )
A. 三个点确定一个圆 B.每条边都相等的多边形是正多边形
C.平分弦的直径垂直于弦 D.直径所对的圆周角是直角
2.如图⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是( )
A.4 B.6 C.8 D.10
第2题图 第3题图 第5题图 第6题图
3.如图,AB是⊙O的直径,点C,D在⊙O上,且OD经过AC的中点E,连结DC并延长,与AB的延长线相交于点P,若∠CAB=16°,则∠BPC的度数为( )
A.16° B.21° C.32° D.37°
4.以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.﹣2 C.﹣22 D.﹣2<b<2
5.如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现( )
A.3次 B.5次 C.6次 D.7次
6.如图,在半径为4的扇形OAB中,∠AOB=90°,点C是AB上一动点,点D是OC的中点,连结AD并延长交OB于点E,则图中阴影部分面积的最小值为( )
A.4π﹣4 B.4π﹣ C.2π﹣4 D.2π﹣
7、下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆心角为120°的扇形面积S与半径R之间的关系
8. 圆的半径为5cm,若其半径增加xcm,其面积增加ycm2,y是x的二次函数,其函数表达式为( )
A. y=πx2 B. y=π(x+5)2 C. y=πx2+10πx D. y=πx2+10x+25
9.如图,圆锥的底面半径R=3,母线l=5dm,AB为底面直径,C为底面圆周上一点,∠COB=150°,D为VB上一点,VD=.现有一只蚂蚁,沿圆锥表面从点C爬到D.则蚂蚁爬行的最短路程是( )
A.3 B.4 C. D.2
第9题图 第10题图 第12题图
10. 在矩形ABCD中,AB=10,AD=6,点N是线段BC的中点,点E、G分别为射线DA,线段AB上的动点,CE交以DE为直径的圆于点M,则GM+GN的最小值为( ).
A. B. C. 5 D. 6
二.填空题(每小题3分 共30分)
11.在矩形ABCD中,BC=6,CD=8,以点A为圆心画圆,且点D在⊙A的内部,点B在⊙A的外部,则⊙A的半径r的取值范围是 .
12.如图正六边形ABCDEF内接于⊙O,若⊙O的周长为8π,则正六边形的边长为 .
13.如图,已知⊙O上有三点A、B、C,半径OC=2,∠ABC=30°,切线AP交OC延长线于点P,则△OAP的周长为______________
第13题图 第14题图 第16题图 第17题图
14. 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,且点A的坐标为,D为第一象限内上的一点,若,则____.
15.在平面直角坐标系中,⊙P经过点A(0,)、B(0,3),⊙P与x轴相切于点C,则点P的坐标是_____________
16.如图,AB是半圆O的直径,点C在半圆上.AB=5,AC=4,D是上的一个动点,连接AD.过点C作CE⊥AD于E.连接BE,则BE的最小值是__________.
17. 如图在Rt△ABC中,AB⊥BC、AB=6,BC=4,点P是△ABC内部的一个动点,连接PC,且满足∠PAB=∠PBC,过点P作PD⊥BC交BC于点D当线段CP最短时,△BCP的面积为______;
18.观察下列各图中小球的摆放规律,若第n个图中小球的个数为y,则y与n的函数关系式为
第18题图 第19题图 第20题图
19.如图,在直角梯形ABCD中,BF=AE=DG=x,AB=6,CD=3,AD=4,则四边形CGEF的面积y与x之间的函数关系式为 ,
20.如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是___________.
三.解答题(60分)
21.(8分)已知y=(m-4)+2x2-3x-1是y关于x的函数.
(1)当m为何值时,它是y关于x的一次函数
(2)当m为何值时,它是y关于x的二次函数
22.(8分)如图,⊙O的直径AB=12 cm,有一条定长为8 cm的动弦CD在上滑动(点C不与A,B重合,点D也不与A,B重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出证明,并求出这个定值;若不是,请说明理由.
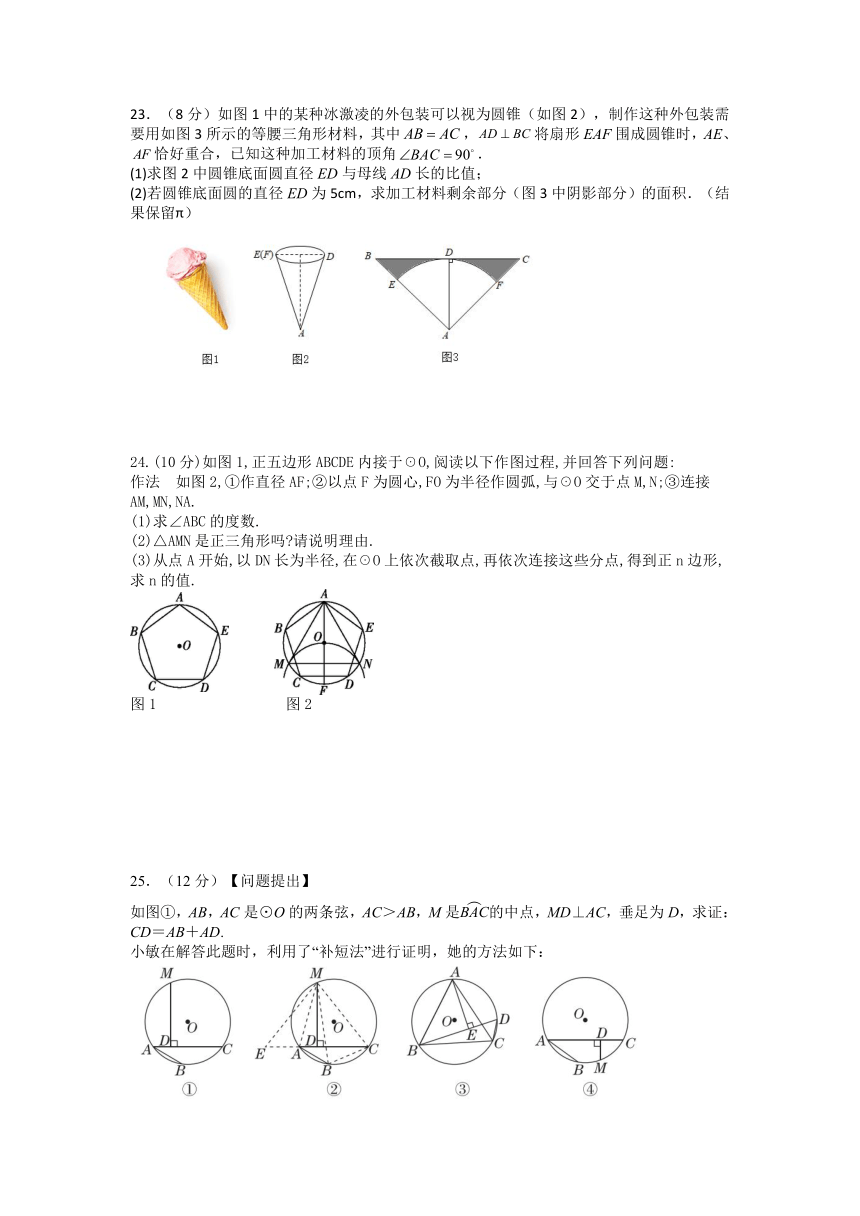
23.(8分)如图1中的某种冰激凌的外包装可以视为圆锥(如图2),制作这种外包装需要用如图3所示的等腰三角形材料,其中,将扇形EAF围成圆锥时,AE、恰好重合,已知这种加工材料的顶角.
(1)求图2中圆锥底面圆直径ED与母线AD长的比值;
(2)若圆锥底面圆的直径ED为5cm,求加工材料剩余部分(图3中阴影部分)的面积.(结果保留π)
24.(10分)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题:
作法 如图2,①作直径AF;②以点F为圆心,FO为半径作圆弧,与☉O交于点M,N;③连接AM,MN,NA.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗 请说明理由.
(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
图1 图2
25.(12分)【问题提出】
如图①,AB,AC是⊙O的两条弦,AC>AB,M是的中点,MD⊥AC,垂足为D,求证:CD=AB+AD.
小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
证明:如图②,延长CA至点E,使AE=AB,连结MA,MB,MC,ME,BC.
∵M是的中点,∴=,
∴∠MCB=∠MBC,MB=MC.(请你在下面的空白处补全小敏的证明过程)
【推广运用】
如图③,等边三角形ABC内接于⊙O,AB=1,D是上一点,∠ABD=45°,AE⊥BD,垂足为E,则△BDC的周长是________.
【拓展研究】
如图④,若将【问题提出】中的“M是的中点”改成“M是的中点”,其余条件不变,“CD=AB+AD”这一结论还成立吗?若成立,请说明理由;若不成立,请写出CD,AB,AD三者之间的数量关系,并说明理由.
26.(14分)对于一平面图形而言,若点M、N是该图形上的任意两点,我们规定:线段MN长度的最大值称为该平面图形S的“绝对距离”.例如,圆的“绝对距离”等于它的直径.如图2,在平面直角坐标系中,已知点A(0,﹣1)、B(0,1),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的“绝对距离”为d.
(1)写出下列图形的“绝对距离”:①边长为1的正方形的“绝对距离: ;②如图1,上方是半径为1的半圆,下方是等边三角形的“绝对距离”: ;(2)动点C从(﹣5,0)出发,沿x轴以每秒一个单位的速度向右运动,当d=3时,请求出t的值;(3)若点C在⊙M上运动,⊙M的半径为1,圆心M在x轴上运动.对于⊙M上任意点C,都有4≤d≤8,直接写出圆心M的横坐标x的取值范围.
教师样卷
一.选择题(每小题3分 共30分)
1.下列事件中,属于必然事件的是( C )
A. 三个点确定一个圆 B.每条边都相等的多边形是正多边形
C.平分弦的直径垂直于弦 D.直径所对的圆周角是直角
2.如图⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是( D )
A.4 B.6 C.8 D.10
第2题图 第3题图 第5题图 第6题图
3.如图,AB是⊙O的直径,点C,D在⊙O上,且OD经过AC的中点E,连结DC并延长,与AB的延长线相交于点P,若∠CAB=16°,则∠BPC的度数为( B )
A.16° B.21° C.32° D.37°
4.以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( D )
A.0≤b<2 B.﹣2 C.﹣22 D.﹣2<b<2
5.如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现( B )
A.3次 B.5次 C.6次 D.7次
解:∵⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,设O1O2交圆O于M,∴PM=8﹣3﹣1=4,圆O1与以P为圆心,以4为半径的圆相外切,∴根据图形得出有5次.故选:B.
6.如图,在半径为4的扇形OAB中,∠AOB=90°,点C是AB上一动点,点D是OC的中点,连结AD并延长交OB于点E,则图中阴影部分面积的最小值为( B )
A.4π﹣4 B.4π﹣ C.2π﹣4 D.2π﹣
解:∵点D是OC的中点,OC=4,∴OD=2,OA=4,∴点D在以点O为圆心2为半径的圆弧上,∴当AE′与小圆O相切时,OE′最大,此时OC′与小圆O交于点D′,∵OA=4,∠AOE=90°,∴当OE最大时,阴影部分取得最小值,∵∠AD′O=90°,OD′=2,OA=4,∴OA=2OD′,∴∠OAD′=30°,∴OE′=,∴图中阴影部分面积的最小值为:=4π﹣,故选:B.
7、下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆心角为120°的扇形面积S与半径R之间的关系
8. 圆的半径为5cm,若其半径增加xcm,其面积增加ycm2,y是x的二次函数,其函数表达式为( C )
A. y=πx2 B. y=π(x+5)2 C. y=πx2+10πx D. y=πx2+10x+25
9.如图,圆锥的底面半径R=3,母线l=5dm,AB为底面直径,C为底面圆周上一点,∠COB=150°,D为VB上一点,VD=.现有一只蚂蚁,沿圆锥表面从点C爬到D.则蚂蚁爬行的最短路程是( B )
A.3 B.4 C. D.2
解:如图:∵,∴设弧所对的圆心角的度数为n,∴,解得,∴,∴.故选:B.
第9题图 第10题图 第12题图
10. 在矩形ABCD中,AB=10,AD=6,点N是线段BC的中点,点E、G分别为射线DA,线段AB上的动点,CE交以DE为直径的圆于点M,则GM+GN的最小值为( A ).
A. B. C. 5 D. 6
解:作点N关于AB的对称点H,取CD的中点F,连接FH,交AB于点G,连接DM、FM、GM、NG,如图所示,当H、M、F、G1在同一直线上时,GM+GN最小,最小值为FH-FM,∵在矩形ABCD中,AB=10,AD=6,∴CD=10,BC=6,∠ABC=90°,∵DE为直径,∴∠DME=∠DMC=90°,
∵CD的中点为F,AB=10,∴FM= FM=5,由对称可知,BH=BN= ,CH=9,
,GM+GN最小值为,故选:A.
二.填空题(每小题3分 共30分)
11.在矩形ABCD中,BC=6,CD=8,以点A为圆心画圆,且点D在⊙A的内部,点B在⊙A的外部,则⊙A的半径r的取值范围是 6<r<8 .
解:∵四边形ABCD是矩形,∴AB=CD=8,AD=BC=6,∵点D在⊙A内,点B在⊙A外,∴6<r<8.故答案为:6<r<8.
12.如图正六边形ABCDEF内接于⊙O,若⊙O的周长为8π,则正六边形的边长为 4 .
解:连接OA,OB,∵正六边形ABCDEF内接于⊙O,⊙O的周长为8π,∴⊙O的半径为4,
∵∠AOB==60°,∴△AOB是等边三角形,∴AB=OA=4,∴正六边形ABCDEF的边长为4,故答案为:4.
13.如图,已知⊙O上有三点A、B、C,半径OC=2,∠ABC=30°,切线AP交OC延长线于点P,则△OAP的周长为______________
解:连接OA,如下图..为的切线,
,,.,,,的周长为.故答案为:.
第13题图 第14题图 第16题图 第17题图
14. 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,且点A的坐标为,D为第一象限内上的一点,若,则____.
解:连接OD,BD,∵,∴∠EOD=2,∵,
∴,∴,∵AB为圆的直径,∴,∴BD=,
∴,故答案为:.
15.在平面直角坐标系中,⊙P经过点A(0,)、B(0,3),⊙P与x轴相切于点C,则点P的坐标是__(3,2)或(﹣3,2)___________
解:如图1,过P作PD⊥y轴于D,连接PC,∵⊙P与x轴相切于点C,∴PC⊥x轴,
∴四边形OCPD是矩形,∴PC=OD,PD=OC,∵点A(0,)、B(0,3),∴AB=2,
∴BD=AD=AB=,∵∠PCO=∠PDO=∠COD=90°,∴四边形PCOD是矩形,∴PC=OD=2,连接PB,∴PB=PC=2,在Rt△PBD中,PD===3,∴P(3,2);如图2,同理可得,P(﹣3,2),综上所述,点P的坐标是(3,2)或(﹣3,2),
16.如图,AB是半圆O的直径,点C在半圆上.AB=5,AC=4,D是上的一个动点,连接AD.过点C作CE⊥AD于E.连接BE,则BE的最小值是__﹣2__________.
解:如图,取AC的中点O′,连接BO′、BC.∵CE⊥AD,∴∠AEC=90°,∴在点D移动的过程中,点E在以AC为直径的圆上运动,∵AB是直径,∴∠ACB=90°,在Rt△ABC中,∵AC=4,AB=5,∴BC==3,在Rt△BCO′中,BO′==,∵O′E+BE≥O′B,∴当O′、E、B共线时,BE的值最小,最小值为O′B﹣O′E=﹣2,
17. 如图,在Rt△ABC中,AB⊥BC、AB=6,BC=4,点P是△ABC内部的一个动点,连接PC,且满足∠PAB=∠PBC,过点P作PD⊥BC交BC于点D当线段CP最短时,△BCP的面积为______________;
解: 设的中点为,连接, 则,点在以为直径的上,连接交于点,此时最小, 在中, , ,, , , ,
, .故答案为:.
18.观察下列各图中小球的摆放规律,若第n个图中小球的个数为y,则y与n的函数关系式为 y=n2﹣n+1
解:根据题意分析可得:第n个图中,从中心点分出n个分支,每个分支上有(n﹣1)个点,不含中心点; 则第n个图中小黑点的个数y=n×(n﹣1)+1=n2﹣n+1.即y与n的函数关系式为 y=n2﹣n+1.故答案为:y=n2﹣n+1.
第18题图 第19题图 第20题图
19.如图,在直角梯形ABCD中,BF=AE=DG=x,AB=6,CD=3,AD=4,则四边形CGEF的面积y与x之间的函数关系式为 y=x2﹣7x+18,0<x<3. ,
解:由题意可得: y=S梯形ABCD﹣S△DGE﹣S△EAF﹣S△BFC= (3+6)×4﹣ x×(4﹣x)﹣ x×(6﹣x)﹣ x×4=18+ x2﹣2x+ x2﹣3x﹣2x=x2﹣7x+18,(0<x<3)
故答案为:y=x2﹣7x+18,0<x<3.
20.如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是___y= x2_________.
解:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE∴∠BAC=∠DAE又∵AB=AD,∠ACB=∠E=90°
∴△ABC≌△ADE(AAS)∴BC=DE,AC=AE,设BC=a,则DE=a,DF=AE=AC=4BC=4a,
CF=AC﹣AF=AC﹣DE=3a,在Rt△CDF中,由勾股定理得,CF2+DF2=CD2,即(3a)2+(4a)2=x2,解得:a= ,∴y=S四边形ABCD=S梯形ACDE= ×(DE+AC)×DF= ×(a+4a)×4a
=10a2= x2.
三.解答题(60分)
21.(8分)已知y=(m-4)+2x2-3x-1是y关于x的函数.
(1)当m为何值时,它是y关于x的一次函数
(2)当m为何值时,它是y关于x的二次函数
解:(1)由y=(m-4)+2x2-3x-1是y关于x的一次函数,得
解得m=2,∴当m=2时,它是y关于x的一次函数.
(2)由y=(m-4)+2x2-3x-1是y关于x的二次函数,得①m-4=0,解得m=4;②m2-m=1,解得m=;③解得m=-1; ④m2-m=0,解得m=0或m=1.综上所述,当m=0,m=1,m=4,m=或m=-1时,它是y关于x的二次函数.
22.(8分)如图,⊙O的直径AB=12 cm,有一条定长为8 cm的动弦CD在上滑动(点C不与A,B重合,点D也不与A,B重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出证明,并求出这个定值;若不是,请说明理由.
解:(1)证明:过点O作OH⊥CD于点H,易得H为CD的中点.
∵CE⊥CD,DF⊥CD,∴EC∥OH∥FD,易得O为EF的中点,即OE=OF.
又∵OA=OB,∴AE=OA-OE=OB-OF=BF,即AE=BF.
(2)解:四边形CDFE的面积为定值.证明如下:∵动弦CD在滑动的过程中,条件EC⊥CD,FD⊥CD不变,∴CE∥DF不变.由此可知,四边形CDFE为直角梯形或矩形,易得S四边形CDFE=OH·CD.连结OC,由勾股定理得OH===2(cm).又∵CD=8 cm,∴S四边形CDFE=OH·CD=2×8=16(cm2),是常数.综上,四边形CDFE的面积为定值,为16cm2.
23.(8分)如图1中的某种冰激凌的外包装可以视为圆锥(如图2),制作这种外包装需要用如图3所示的等腰三角形材料,其中,将扇形EAF围成圆锥时,AE、恰好重合,已知这种加工材料的顶角.
(1)求图2中圆锥底面圆直径ED与母线AD长的比值;
(2)若圆锥底面圆的直径ED为5cm,求加工材料剩余部分(图3中阴影部分)的面积.(结果保留π)
解:(1)由圆锥的底面圆周长相当于侧面展开后扇形的弧长得:.
∴.∴,ED与母线AD长之比为
(2)∵∴
答:加工材料剩余部分的面积为
24.(10分)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题:
作法 如图2,①作直径AF;②以点F为圆心,FO为半径作圆弧,与☉O交于点M,N;③连接AM,MN,NA.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗 请说明理由.
(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
图1 图2
解:(1)∵五边形ABCDE是正五边形,∴∠ABC==108°.
(2)△AMN是正三角形.理由如下:连接ON,NF,如图.由题意可得,FN=ON=OF,∴△FON是等边三角形,∴∠NFA=60°,∴∠NMA=60°.同理可得,∠ANM=60°,∴∠MAN=60°,∴△MAN是正三角形.
(3)连接OD,如图.∵∠AMN=60°,∴∠AON=120°.∵∠AOD=×2=144°,∴∠NOD=∠AOD-∠AON=144°-120°=24°.∵360°÷24°=15,∴n的值是15.
25.(12分)【问题提出】
如图①,AB,AC是⊙O的两条弦,AC>AB,M是的中点,MD⊥AC,垂足为D,求证:CD=AB+AD.
小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
证明:如图②,延长CA至点E,使AE=AB,连结MA,MB,MC,ME,BC.
∵M是的中点,∴=,
∴∠MCB=∠MBC,MB=MC.(请你在下面的空白处补全小敏的证明过程)
【推广运用】
如图③,等边三角形ABC内接于⊙O,AB=1,D是上一点,∠ABD=45°,AE⊥BD,垂足为E,则△BDC的周长是________.
【拓展研究】
如图④,若将【问题提出】中的“M是的中点”改成“M是的中点”,其余条件不变,“CD=AB+AD”这一结论还成立吗?若成立,请说明理由;若不成立,请写出CD,AB,AD三者之间的数量关系,并说明理由.
解:【问题提出】∵∠MAC=∠MBC,∴∠EAM=180°-∠MAC=180°-∠MBC.
又∵∠BAM=180°-∠MCB,∴∠EAM=∠BAM.在△EAM 和△BAM 中,∴△EAM≌△BAM,∴ME=MB=MC.又∵MD⊥AC,∴ED=CD,
∴CD=AE+AD=AB+AD.
【推广运用】1+
【拓展研究】不成立,AD=AB+CD,理由:如图,延长MD交⊙O于点E,连结EA,EC,EB,EB交AC于点N.∵M是的中点,∴=.∴∠BEM=∠CEM.在△EDN 和△EDC 中, ∴△EDN≌△EDC,∴ND=CD,∠END=∠ECD.又∵∠ECD=∠ABE,∠END=∠ANB,∴∠ANB=∠ABE,∴AN=AB,∴AD=AN+ND=AB+CD.
26.(14分)对于一平面图形而言,若点M、N是该图形上的任意两点,我们规定:线段MN长度的最大值称为该平面图形S的“绝对距离”.例如,圆的“绝对距离”等于它的直径.如图2,在平面直角坐标系中,已知点A(0,﹣1)、B(0,1),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的“绝对距离”为d.
(1)写出下列图形的“绝对距离”:①边长为1的正方形的“绝对距离: ;②如图1,上方是半径为1的半圆,下方是等边三角形的“绝对距离”: ;(2)动点C从(﹣5,0)出发,沿x轴以每秒一个单位的速度向右运动,当d=3时,请求出t的值;(3)若点C在⊙M上运动,⊙M的半径为1,圆心M在x轴上运动.对于⊙M上任意点C,都有4≤d≤8,直接写出圆心M的横坐标x的取值范围.
解:(1)①∵边长为1的正方形的“绝对距离是对角线的长,∴边长为1的正方形的“绝对距离=,
②如图1,∴上方是半径为1的半圆,下方是等边三角形的“绝对距离”是CH,
∴CH=1+,故答案为:,1+;
(2)如图2中,∵A(0,﹣10,B(0,1),∴OA=OB=1,AB=2,∵CO⊥AB,∴CA=CB,
∵d=3,不妨设AC=BC=3,则OC===2,∴t=5﹣2或=5+2.
(3)如图3中,如图2﹣2中,当点M在y轴的右侧时,连接AM.∵对于⊙M上任意点C,都有4≤d≤8,∴当d=4时,AM=5,∴OM===2,此时M(2,0),当d=8时,AM=7,∴OM===4,此时M(4,0),
∴满足条件的点M的横坐标的范围为2≤x≤4.当点M在y轴的左侧时,满足条件的点M的横坐标的范围为﹣4≤x≤﹣2,综上所述,满足条件的圆心M的横坐标x的取值范围为2≤x≤4或﹣4≤x≤﹣2.
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共30分)
1.下列事件中,属于必然事件的是( )
A. 三个点确定一个圆 B.每条边都相等的多边形是正多边形
C.平分弦的直径垂直于弦 D.直径所对的圆周角是直角
2.如图⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是( )
A.4 B.6 C.8 D.10
第2题图 第3题图 第5题图 第6题图
3.如图,AB是⊙O的直径,点C,D在⊙O上,且OD经过AC的中点E,连结DC并延长,与AB的延长线相交于点P,若∠CAB=16°,则∠BPC的度数为( )
A.16° B.21° C.32° D.37°
4.以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.﹣2 C.﹣22 D.﹣2<b<2
5.如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现( )
A.3次 B.5次 C.6次 D.7次
6.如图,在半径为4的扇形OAB中,∠AOB=90°,点C是AB上一动点,点D是OC的中点,连结AD并延长交OB于点E,则图中阴影部分面积的最小值为( )
A.4π﹣4 B.4π﹣ C.2π﹣4 D.2π﹣
7、下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆心角为120°的扇形面积S与半径R之间的关系
8. 圆的半径为5cm,若其半径增加xcm,其面积增加ycm2,y是x的二次函数,其函数表达式为( )
A. y=πx2 B. y=π(x+5)2 C. y=πx2+10πx D. y=πx2+10x+25
9.如图,圆锥的底面半径R=3,母线l=5dm,AB为底面直径,C为底面圆周上一点,∠COB=150°,D为VB上一点,VD=.现有一只蚂蚁,沿圆锥表面从点C爬到D.则蚂蚁爬行的最短路程是( )
A.3 B.4 C. D.2
第9题图 第10题图 第12题图
10. 在矩形ABCD中,AB=10,AD=6,点N是线段BC的中点,点E、G分别为射线DA,线段AB上的动点,CE交以DE为直径的圆于点M,则GM+GN的最小值为( ).
A. B. C. 5 D. 6
二.填空题(每小题3分 共30分)
11.在矩形ABCD中,BC=6,CD=8,以点A为圆心画圆,且点D在⊙A的内部,点B在⊙A的外部,则⊙A的半径r的取值范围是 .
12.如图正六边形ABCDEF内接于⊙O,若⊙O的周长为8π,则正六边形的边长为 .
13.如图,已知⊙O上有三点A、B、C,半径OC=2,∠ABC=30°,切线AP交OC延长线于点P,则△OAP的周长为______________
第13题图 第14题图 第16题图 第17题图
14. 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,且点A的坐标为,D为第一象限内上的一点,若,则____.
15.在平面直角坐标系中,⊙P经过点A(0,)、B(0,3),⊙P与x轴相切于点C,则点P的坐标是_____________
16.如图,AB是半圆O的直径,点C在半圆上.AB=5,AC=4,D是上的一个动点,连接AD.过点C作CE⊥AD于E.连接BE,则BE的最小值是__________.
17. 如图在Rt△ABC中,AB⊥BC、AB=6,BC=4,点P是△ABC内部的一个动点,连接PC,且满足∠PAB=∠PBC,过点P作PD⊥BC交BC于点D当线段CP最短时,△BCP的面积为______;
18.观察下列各图中小球的摆放规律,若第n个图中小球的个数为y,则y与n的函数关系式为
第18题图 第19题图 第20题图
19.如图,在直角梯形ABCD中,BF=AE=DG=x,AB=6,CD=3,AD=4,则四边形CGEF的面积y与x之间的函数关系式为 ,
20.如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是___________.
三.解答题(60分)
21.(8分)已知y=(m-4)+2x2-3x-1是y关于x的函数.
(1)当m为何值时,它是y关于x的一次函数
(2)当m为何值时,它是y关于x的二次函数
22.(8分)如图,⊙O的直径AB=12 cm,有一条定长为8 cm的动弦CD在上滑动(点C不与A,B重合,点D也不与A,B重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出证明,并求出这个定值;若不是,请说明理由.
23.(8分)如图1中的某种冰激凌的外包装可以视为圆锥(如图2),制作这种外包装需要用如图3所示的等腰三角形材料,其中,将扇形EAF围成圆锥时,AE、恰好重合,已知这种加工材料的顶角.
(1)求图2中圆锥底面圆直径ED与母线AD长的比值;
(2)若圆锥底面圆的直径ED为5cm,求加工材料剩余部分(图3中阴影部分)的面积.(结果保留π)
24.(10分)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题:
作法 如图2,①作直径AF;②以点F为圆心,FO为半径作圆弧,与☉O交于点M,N;③连接AM,MN,NA.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗 请说明理由.
(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
图1 图2
25.(12分)【问题提出】
如图①,AB,AC是⊙O的两条弦,AC>AB,M是的中点,MD⊥AC,垂足为D,求证:CD=AB+AD.
小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
证明:如图②,延长CA至点E,使AE=AB,连结MA,MB,MC,ME,BC.
∵M是的中点,∴=,
∴∠MCB=∠MBC,MB=MC.(请你在下面的空白处补全小敏的证明过程)
【推广运用】
如图③,等边三角形ABC内接于⊙O,AB=1,D是上一点,∠ABD=45°,AE⊥BD,垂足为E,则△BDC的周长是________.
【拓展研究】
如图④,若将【问题提出】中的“M是的中点”改成“M是的中点”,其余条件不变,“CD=AB+AD”这一结论还成立吗?若成立,请说明理由;若不成立,请写出CD,AB,AD三者之间的数量关系,并说明理由.
26.(14分)对于一平面图形而言,若点M、N是该图形上的任意两点,我们规定:线段MN长度的最大值称为该平面图形S的“绝对距离”.例如,圆的“绝对距离”等于它的直径.如图2,在平面直角坐标系中,已知点A(0,﹣1)、B(0,1),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的“绝对距离”为d.
(1)写出下列图形的“绝对距离”:①边长为1的正方形的“绝对距离: ;②如图1,上方是半径为1的半圆,下方是等边三角形的“绝对距离”: ;(2)动点C从(﹣5,0)出发,沿x轴以每秒一个单位的速度向右运动,当d=3时,请求出t的值;(3)若点C在⊙M上运动,⊙M的半径为1,圆心M在x轴上运动.对于⊙M上任意点C,都有4≤d≤8,直接写出圆心M的横坐标x的取值范围.
教师样卷
一.选择题(每小题3分 共30分)
1.下列事件中,属于必然事件的是( C )
A. 三个点确定一个圆 B.每条边都相等的多边形是正多边形
C.平分弦的直径垂直于弦 D.直径所对的圆周角是直角
2.如图⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是( D )
A.4 B.6 C.8 D.10
第2题图 第3题图 第5题图 第6题图
3.如图,AB是⊙O的直径,点C,D在⊙O上,且OD经过AC的中点E,连结DC并延长,与AB的延长线相交于点P,若∠CAB=16°,则∠BPC的度数为( B )
A.16° B.21° C.32° D.37°
4.以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( D )
A.0≤b<2 B.﹣2 C.﹣22 D.﹣2<b<2
5.如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现( B )
A.3次 B.5次 C.6次 D.7次
解:∵⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,设O1O2交圆O于M,∴PM=8﹣3﹣1=4,圆O1与以P为圆心,以4为半径的圆相外切,∴根据图形得出有5次.故选:B.
6.如图,在半径为4的扇形OAB中,∠AOB=90°,点C是AB上一动点,点D是OC的中点,连结AD并延长交OB于点E,则图中阴影部分面积的最小值为( B )
A.4π﹣4 B.4π﹣ C.2π﹣4 D.2π﹣
解:∵点D是OC的中点,OC=4,∴OD=2,OA=4,∴点D在以点O为圆心2为半径的圆弧上,∴当AE′与小圆O相切时,OE′最大,此时OC′与小圆O交于点D′,∵OA=4,∠AOE=90°,∴当OE最大时,阴影部分取得最小值,∵∠AD′O=90°,OD′=2,OA=4,∴OA=2OD′,∴∠OAD′=30°,∴OE′=,∴图中阴影部分面积的最小值为:=4π﹣,故选:B.
7、下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆心角为120°的扇形面积S与半径R之间的关系
8. 圆的半径为5cm,若其半径增加xcm,其面积增加ycm2,y是x的二次函数,其函数表达式为( C )
A. y=πx2 B. y=π(x+5)2 C. y=πx2+10πx D. y=πx2+10x+25
9.如图,圆锥的底面半径R=3,母线l=5dm,AB为底面直径,C为底面圆周上一点,∠COB=150°,D为VB上一点,VD=.现有一只蚂蚁,沿圆锥表面从点C爬到D.则蚂蚁爬行的最短路程是( B )
A.3 B.4 C. D.2
解:如图:∵,∴设弧所对的圆心角的度数为n,∴,解得,∴,∴.故选:B.
第9题图 第10题图 第12题图
10. 在矩形ABCD中,AB=10,AD=6,点N是线段BC的中点,点E、G分别为射线DA,线段AB上的动点,CE交以DE为直径的圆于点M,则GM+GN的最小值为( A ).
A. B. C. 5 D. 6
解:作点N关于AB的对称点H,取CD的中点F,连接FH,交AB于点G,连接DM、FM、GM、NG,如图所示,当H、M、F、G1在同一直线上时,GM+GN最小,最小值为FH-FM,∵在矩形ABCD中,AB=10,AD=6,∴CD=10,BC=6,∠ABC=90°,∵DE为直径,∴∠DME=∠DMC=90°,
∵CD的中点为F,AB=10,∴FM= FM=5,由对称可知,BH=BN= ,CH=9,
,GM+GN最小值为,故选:A.
二.填空题(每小题3分 共30分)
11.在矩形ABCD中,BC=6,CD=8,以点A为圆心画圆,且点D在⊙A的内部,点B在⊙A的外部,则⊙A的半径r的取值范围是 6<r<8 .
解:∵四边形ABCD是矩形,∴AB=CD=8,AD=BC=6,∵点D在⊙A内,点B在⊙A外,∴6<r<8.故答案为:6<r<8.
12.如图正六边形ABCDEF内接于⊙O,若⊙O的周长为8π,则正六边形的边长为 4 .
解:连接OA,OB,∵正六边形ABCDEF内接于⊙O,⊙O的周长为8π,∴⊙O的半径为4,
∵∠AOB==60°,∴△AOB是等边三角形,∴AB=OA=4,∴正六边形ABCDEF的边长为4,故答案为:4.
13.如图,已知⊙O上有三点A、B、C,半径OC=2,∠ABC=30°,切线AP交OC延长线于点P,则△OAP的周长为______________
解:连接OA,如下图..为的切线,
,,.,,,的周长为.故答案为:.
第13题图 第14题图 第16题图 第17题图
14. 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,且点A的坐标为,D为第一象限内上的一点,若,则____.
解:连接OD,BD,∵,∴∠EOD=2,∵,
∴,∴,∵AB为圆的直径,∴,∴BD=,
∴,故答案为:.
15.在平面直角坐标系中,⊙P经过点A(0,)、B(0,3),⊙P与x轴相切于点C,则点P的坐标是__(3,2)或(﹣3,2)___________
解:如图1,过P作PD⊥y轴于D,连接PC,∵⊙P与x轴相切于点C,∴PC⊥x轴,
∴四边形OCPD是矩形,∴PC=OD,PD=OC,∵点A(0,)、B(0,3),∴AB=2,
∴BD=AD=AB=,∵∠PCO=∠PDO=∠COD=90°,∴四边形PCOD是矩形,∴PC=OD=2,连接PB,∴PB=PC=2,在Rt△PBD中,PD===3,∴P(3,2);如图2,同理可得,P(﹣3,2),综上所述,点P的坐标是(3,2)或(﹣3,2),
16.如图,AB是半圆O的直径,点C在半圆上.AB=5,AC=4,D是上的一个动点,连接AD.过点C作CE⊥AD于E.连接BE,则BE的最小值是__﹣2__________.
解:如图,取AC的中点O′,连接BO′、BC.∵CE⊥AD,∴∠AEC=90°,∴在点D移动的过程中,点E在以AC为直径的圆上运动,∵AB是直径,∴∠ACB=90°,在Rt△ABC中,∵AC=4,AB=5,∴BC==3,在Rt△BCO′中,BO′==,∵O′E+BE≥O′B,∴当O′、E、B共线时,BE的值最小,最小值为O′B﹣O′E=﹣2,
17. 如图,在Rt△ABC中,AB⊥BC、AB=6,BC=4,点P是△ABC内部的一个动点,连接PC,且满足∠PAB=∠PBC,过点P作PD⊥BC交BC于点D当线段CP最短时,△BCP的面积为______________;
解: 设的中点为,连接, 则,点在以为直径的上,连接交于点,此时最小, 在中, , ,, , , ,
, .故答案为:.
18.观察下列各图中小球的摆放规律,若第n个图中小球的个数为y,则y与n的函数关系式为 y=n2﹣n+1
解:根据题意分析可得:第n个图中,从中心点分出n个分支,每个分支上有(n﹣1)个点,不含中心点; 则第n个图中小黑点的个数y=n×(n﹣1)+1=n2﹣n+1.即y与n的函数关系式为 y=n2﹣n+1.故答案为:y=n2﹣n+1.
第18题图 第19题图 第20题图
19.如图,在直角梯形ABCD中,BF=AE=DG=x,AB=6,CD=3,AD=4,则四边形CGEF的面积y与x之间的函数关系式为 y=x2﹣7x+18,0<x<3. ,
解:由题意可得: y=S梯形ABCD﹣S△DGE﹣S△EAF﹣S△BFC= (3+6)×4﹣ x×(4﹣x)﹣ x×(6﹣x)﹣ x×4=18+ x2﹣2x+ x2﹣3x﹣2x=x2﹣7x+18,(0<x<3)
故答案为:y=x2﹣7x+18,0<x<3.
20.如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是___y= x2_________.
解:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE∴∠BAC=∠DAE又∵AB=AD,∠ACB=∠E=90°
∴△ABC≌△ADE(AAS)∴BC=DE,AC=AE,设BC=a,则DE=a,DF=AE=AC=4BC=4a,
CF=AC﹣AF=AC﹣DE=3a,在Rt△CDF中,由勾股定理得,CF2+DF2=CD2,即(3a)2+(4a)2=x2,解得:a= ,∴y=S四边形ABCD=S梯形ACDE= ×(DE+AC)×DF= ×(a+4a)×4a
=10a2= x2.
三.解答题(60分)
21.(8分)已知y=(m-4)+2x2-3x-1是y关于x的函数.
(1)当m为何值时,它是y关于x的一次函数
(2)当m为何值时,它是y关于x的二次函数
解:(1)由y=(m-4)+2x2-3x-1是y关于x的一次函数,得
解得m=2,∴当m=2时,它是y关于x的一次函数.
(2)由y=(m-4)+2x2-3x-1是y关于x的二次函数,得①m-4=0,解得m=4;②m2-m=1,解得m=;③解得m=-1; ④m2-m=0,解得m=0或m=1.综上所述,当m=0,m=1,m=4,m=或m=-1时,它是y关于x的二次函数.
22.(8分)如图,⊙O的直径AB=12 cm,有一条定长为8 cm的动弦CD在上滑动(点C不与A,B重合,点D也不与A,B重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出证明,并求出这个定值;若不是,请说明理由.
解:(1)证明:过点O作OH⊥CD于点H,易得H为CD的中点.
∵CE⊥CD,DF⊥CD,∴EC∥OH∥FD,易得O为EF的中点,即OE=OF.
又∵OA=OB,∴AE=OA-OE=OB-OF=BF,即AE=BF.
(2)解:四边形CDFE的面积为定值.证明如下:∵动弦CD在滑动的过程中,条件EC⊥CD,FD⊥CD不变,∴CE∥DF不变.由此可知,四边形CDFE为直角梯形或矩形,易得S四边形CDFE=OH·CD.连结OC,由勾股定理得OH===2(cm).又∵CD=8 cm,∴S四边形CDFE=OH·CD=2×8=16(cm2),是常数.综上,四边形CDFE的面积为定值,为16cm2.
23.(8分)如图1中的某种冰激凌的外包装可以视为圆锥(如图2),制作这种外包装需要用如图3所示的等腰三角形材料,其中,将扇形EAF围成圆锥时,AE、恰好重合,已知这种加工材料的顶角.
(1)求图2中圆锥底面圆直径ED与母线AD长的比值;
(2)若圆锥底面圆的直径ED为5cm,求加工材料剩余部分(图3中阴影部分)的面积.(结果保留π)
解:(1)由圆锥的底面圆周长相当于侧面展开后扇形的弧长得:.
∴.∴,ED与母线AD长之比为
(2)∵∴
答:加工材料剩余部分的面积为
24.(10分)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题:
作法 如图2,①作直径AF;②以点F为圆心,FO为半径作圆弧,与☉O交于点M,N;③连接AM,MN,NA.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗 请说明理由.
(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
图1 图2
解:(1)∵五边形ABCDE是正五边形,∴∠ABC==108°.
(2)△AMN是正三角形.理由如下:连接ON,NF,如图.由题意可得,FN=ON=OF,∴△FON是等边三角形,∴∠NFA=60°,∴∠NMA=60°.同理可得,∠ANM=60°,∴∠MAN=60°,∴△MAN是正三角形.
(3)连接OD,如图.∵∠AMN=60°,∴∠AON=120°.∵∠AOD=×2=144°,∴∠NOD=∠AOD-∠AON=144°-120°=24°.∵360°÷24°=15,∴n的值是15.
25.(12分)【问题提出】
如图①,AB,AC是⊙O的两条弦,AC>AB,M是的中点,MD⊥AC,垂足为D,求证:CD=AB+AD.
小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
证明:如图②,延长CA至点E,使AE=AB,连结MA,MB,MC,ME,BC.
∵M是的中点,∴=,
∴∠MCB=∠MBC,MB=MC.(请你在下面的空白处补全小敏的证明过程)
【推广运用】
如图③,等边三角形ABC内接于⊙O,AB=1,D是上一点,∠ABD=45°,AE⊥BD,垂足为E,则△BDC的周长是________.
【拓展研究】
如图④,若将【问题提出】中的“M是的中点”改成“M是的中点”,其余条件不变,“CD=AB+AD”这一结论还成立吗?若成立,请说明理由;若不成立,请写出CD,AB,AD三者之间的数量关系,并说明理由.
解:【问题提出】∵∠MAC=∠MBC,∴∠EAM=180°-∠MAC=180°-∠MBC.
又∵∠BAM=180°-∠MCB,∴∠EAM=∠BAM.在△EAM 和△BAM 中,∴△EAM≌△BAM,∴ME=MB=MC.又∵MD⊥AC,∴ED=CD,
∴CD=AE+AD=AB+AD.
【推广运用】1+
【拓展研究】不成立,AD=AB+CD,理由:如图,延长MD交⊙O于点E,连结EA,EC,EB,EB交AC于点N.∵M是的中点,∴=.∴∠BEM=∠CEM.在△EDN 和△EDC 中, ∴△EDN≌△EDC,∴ND=CD,∠END=∠ECD.又∵∠ECD=∠ABE,∠END=∠ANB,∴∠ANB=∠ABE,∴AN=AB,∴AD=AN+ND=AB+CD.
26.(14分)对于一平面图形而言,若点M、N是该图形上的任意两点,我们规定:线段MN长度的最大值称为该平面图形S的“绝对距离”.例如,圆的“绝对距离”等于它的直径.如图2,在平面直角坐标系中,已知点A(0,﹣1)、B(0,1),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的“绝对距离”为d.
(1)写出下列图形的“绝对距离”:①边长为1的正方形的“绝对距离: ;②如图1,上方是半径为1的半圆,下方是等边三角形的“绝对距离”: ;(2)动点C从(﹣5,0)出发,沿x轴以每秒一个单位的速度向右运动,当d=3时,请求出t的值;(3)若点C在⊙M上运动,⊙M的半径为1,圆心M在x轴上运动.对于⊙M上任意点C,都有4≤d≤8,直接写出圆心M的横坐标x的取值范围.
解:(1)①∵边长为1的正方形的“绝对距离是对角线的长,∴边长为1的正方形的“绝对距离=,
②如图1,∴上方是半径为1的半圆,下方是等边三角形的“绝对距离”是CH,
∴CH=1+,故答案为:,1+;
(2)如图2中,∵A(0,﹣10,B(0,1),∴OA=OB=1,AB=2,∵CO⊥AB,∴CA=CB,
∵d=3,不妨设AC=BC=3,则OC===2,∴t=5﹣2或=5+2.
(3)如图3中,如图2﹣2中,当点M在y轴的右侧时,连接AM.∵对于⊙M上任意点C,都有4≤d≤8,∴当d=4时,AM=5,∴OM===2,此时M(2,0),当d=8时,AM=7,∴OM===4,此时M(4,0),
∴满足条件的点M的横坐标的范围为2≤x≤4.当点M在y轴的左侧时,满足条件的点M的横坐标的范围为﹣4≤x≤﹣2,综上所述,满足条件的圆心M的横坐标x的取值范围为2≤x≤4或﹣4≤x≤﹣2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
