苏科版九年级数学下册2023-2024学年6.5相似三角形的性质(第2课时)课件 同步课件(共20张PPT)
文档属性
| 名称 | 苏科版九年级数学下册2023-2024学年6.5相似三角形的性质(第2课时)课件 同步课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 14:30:02 | ||
图片预览







文档简介
(共20张PPT)
第6章 · 图形的相似
6.5 相似三角形的性质(2)
第2课时 相似三角形中对应线段的性质
学习目标
1.理解相似三角形对应线段(高、中线、角平分线)的比等于相似比;
2.利用相似三角形对应线段的性质解决问题.
知识回顾
回顾“相似三角形的面积比等于相似比的平方”这个结论的探究过程,你有什么发现?
A
B
C
A′
B′
C′
D
D′
证明:∵△ABC∽△A′B′C′,
∴ ∠B=∠B',
∵AD⊥BC,A'D′⊥B'C',
∴∠ADB=∠A′D′B'=90°.
∴△ABD∽△A'B'D'.
∴ = =k,
∴ = = =kk=k2
如图,△ABC∽△ A'B'C', △ABC与△ A'B'C'的相似比是k,AD、A 'D'是对应高.
相似三角形对应高的比等于相似比.
类似地,相似三角形对应中线、对应角平分线等对应线段的比是否也等于相似比呢?
思考与探索
A
B
C
A′
B′
C′
E
E′
问题1 如图,△ABC∽△ A'B'C', △ABC与△ A'B'C'的相似比是k,AD、A 'D'是对应中线.
=?
证明:∵△ABC∽△A′B′C′,相似比为k.
∴ = =k,∠B=∠B′,
∵AD、A'D'是中线,
∴ =k,
∴ = ,
∴△ABE∽△A′B′E′.
∴ =k.
思考与探索
A
B
C
A′
B′
C′
F
F′
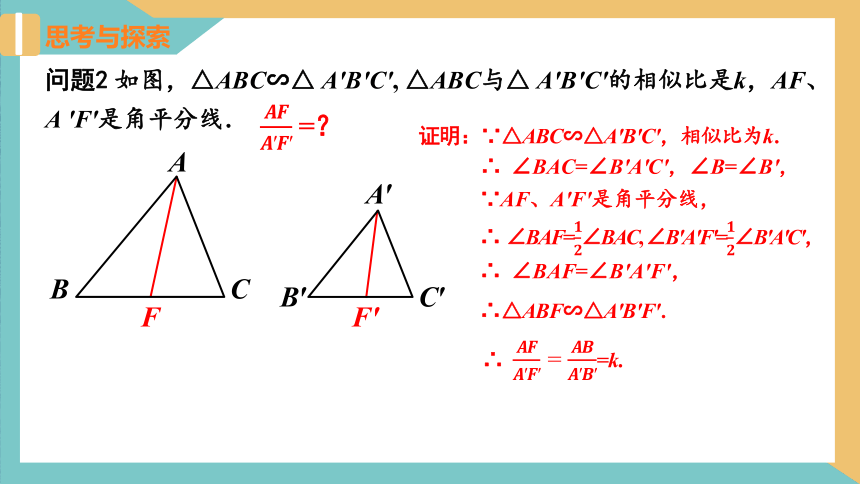
问题2 如图,△ABC∽△ A'B'C', △ABC与△ A'B'C'的相似比是k,AF、A 'F'是角平分线.
=?
证明:∵△ABC∽△A′B′C′,相似比为k.
∴ ∠BAC=∠B′A′C′,∠B=∠B′,
∵AF、A'F'是角平分线,
∴ ∠BAF=∠BAC, ∠B′A′F′=∠B′A′C′,
∴ ∠BAF=∠B′A′F′,
∴△ABF∽△A′B′F′.
∴ =k.
思考与探索
A
B
C
A′
B′
C′
G
G′
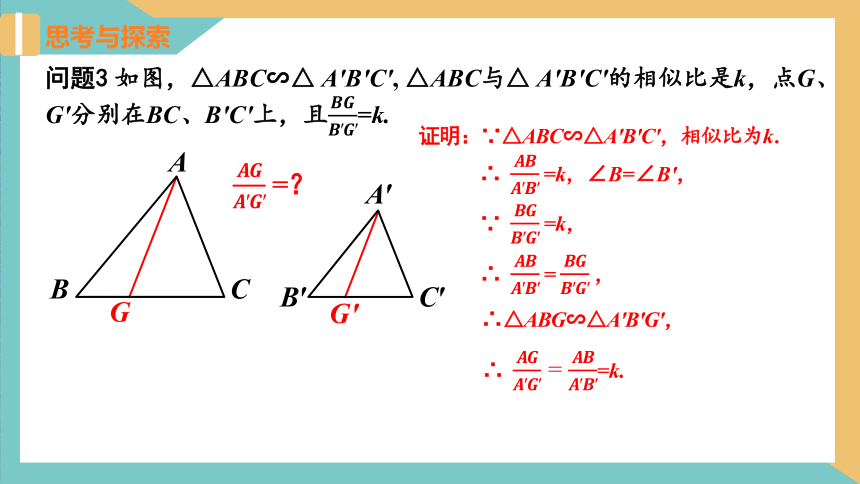
问题3 如图,△ABC∽△ A'B'C', △ABC与△ A'B'C'的相似比是k,点G、G′分别在BC、B′C′上,且=k.
=?
证明:∵△ABC∽△A′B′C′,相似比为k.
∴ =k,∠B=∠B′,
∵ =k,
∴ = ,
∴△ABG∽△A′B′G′,
∴ =k.
相似三角形对应中线等于相似比;
相似三角形对应角平分线等于相似比的平方;
类比与归纳
相似三角形对应线段的比等于相似比的平方.
新知巩固
1. 若两个相似三角形对应高的比为1:3,则它们的相似比为______;对应中线的比为______;对应角平分线的比为______;周长的比为______;面积的比为______.
1 : 3
1 : 3
1 : 3
2.已知两个相似三角形的一组对应高分别是15和5,面积之差为80,则较大三角形的面积为________.
90
1 : 3
1 : 9
新知应用
例 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设DE=6,BC=10,GF=5,求点A到DE、BC的距离.
D
B
C
E
G
F
A
┛
解:由DE∥BC,∠AFB= 90°得
∠AGD=90°,即 AG⊥DE.
可知AG、AF的长分别为点A到DE、BC的距离.
∵DE∥BC,
∴∠ADE= ∠B,∠AED=∠C,∴△ADG∽△FEB,
∴,即,
计算,得AG = 7.5,AF= AG+5 = 12.5,
即点A到DE、BC的距离分别为7.5、12.5.
新知巩固
1.如图,点 D、E分别在 AC、AB上,且∠ADE=∠B,F、G分别是 BC、DE的中点. 设 AD= 3,AB= 5,求的值.
解:∵∠ADE=∠B,∠EAD=∠CAB,
∴△EAD∽△CAB.
∵AG、AF分别是△ADE、△ABC的中线,
∴.
E
B
C
D
G
F
A
新知巩固
2. 如图,在△ABC和△A'B'C'中,AD、A'D'分别是△ABC、△A'B'C' 的角平分线,且AB=2A'B',AC=2A'C',∠BAC=∠B'A'C' 求:
(1)的值;(2)△ABC与△A'B'C'的面积的比.
A
B
C
A′
B′
C′
D
D′
解:(1)∵AB=2A'B',AC=2A'C',
∴2,
∵∠BAC=∠B'A'C' ,
∴△BAC∽△B'A'C' ,
∵AD、A'D'分别是△ABC、△A'B'C' 的角平分线,
∴2.
(2)△ABC与△A'B'C'的面积的比为4.
3. 如图,在△ABC中,AB=AC,正方形DEFG的顶点D、G分别在 AB、AC 上,EF在BC上. 设AB=5,BC=6,求正方形DEFG的边长.
新知巩固
A
B
C
D
G
E
F
M
N
解:设正方形DEFG的边长为x,
作△ABC的高AM,AM交DG于点N.
∵AB=AC,BC=6,
∴BM=CM=BC=×6=3,
∵AM⊥BC,
∴ ∠AMB=90°,
在Rt△AMB中,由勾股定理得AM===4.
∵DG∥BC,
∴△ADG∽△ABC.
∴,
∴,解得x=2.4.
类比归纳
全等三角形与相似三角形性质比较:
全等三角形 相似三角形
对应边( ) 对应边的比等于( )
对应角( ) 对应角( )
周长( ) 周长的比等于( )
面积( ) 面积的比等于( )
对应高( ) 对应高的比等于( )
对应中线( ) 对应中线的比等于( )
对应角平分线( ) 对应角平分线的比等于( )
相等
相等
相等
相等
相等
相等
相等
相等
相似比
相似比
相似比
相似比的平方
相似比
相似比
课堂小结
相似三角形中
对应线段的性质
相似三角形对应中线等于相似比;
相似三角形对应角平分线等于相似比的平方;
相似三角形对应线段的比等于相似比的平方.
当堂检测
1. 用一放大镜看一个直角三角形,该三角形的边长放大到原来的10倍后,下列结论错误的 ( )
A.斜边上的中线是原来的10倍 B.斜边上的高是原来的10倍
C.周长是原来的10倍 D.最小内角是原来的10倍
2. 顺次连接三角形三边的中点,所得的三角形与原三角形对应高的比是( )
A.1:4 B.1:3 C.1: D.1:2
D
D
当堂检测
3. 已知△ABC∽△DEF,面积比为9:4,则△ABC与△DEF的对应角平分线之比为( )A. 4:9 B. 9:4 C. 2:3 D. 3:2
D
4. 在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,AP、DQ 是中线,若 AP=2,则 DQ的值为 ( )
A.2 B.4 C.1 D.
C
当堂检测
5. △ABC 与 △A'B'C' 的面积之比是9:25,若 BC 边上的高 AD=12cm,则 B'C' 边上的高 A'D' =_______ .
20 cm
6. 在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为________.
15.5
B
C
A
D
B
C
A
D(A)
E
F
当堂检测
7.如图,在△ABC中,AD是高,点E、F分别在AB、AC上,且EF∥BC,
EF交AD于点G,. 求:
(1)的值;(2)△AEF与△ABC的面积的比.
E
F
B
C
A
G
D
解:(1)∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠C.
∴△AEF∽△ABC.
∵AG、AD分别是△AEF、△ABC的高,
∴ .
(2)∵△AEF∽△ABC,
∴ .
当堂检测
8. 如图,在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC 上,QM 在 BC上,AD交PN于点 E.设BC = 48,AD=16,PQ:PN=5:9,求矩形PQMN的面积.
A
B
C
P
N
Q
E
D
M
解:∵PN∥BC,
∴∠APN=∠B,∠ANP=∠C.
∴△APN∽△ABC.
∵AE、AD分别是△APN、△ABC的高,
∴ .
即 ,解得PQ=10,PN=PQ=18,
∴矩形PQMN的面积=180.
当堂检测
C
A
B
D
E
9.如图,在四边形ABCD中,点E在AD上,且EC∥AB,EB∥DC.
(1)△ABE与△ECD相似吗?为什么?
(2)设△ABE的边BE上的高为h1,△ECD的边CD上的高为h2,△ABE的面积为3,△ECD的面积为1,求的值以及△BCE的面积.
解:(1)由EC// AB ,EB//DC,得∠A=∠CED,∠AEB=∠D.
∴△ABE∽△ECD.
(2)由题意,得==.
又由EB// DC,得△BCE的边BE上的高与△ECD 的边 CD 上的高相等,
∴ =,
=.
第6章 · 图形的相似
6.5 相似三角形的性质(2)
第2课时 相似三角形中对应线段的性质
学习目标
1.理解相似三角形对应线段(高、中线、角平分线)的比等于相似比;
2.利用相似三角形对应线段的性质解决问题.
知识回顾
回顾“相似三角形的面积比等于相似比的平方”这个结论的探究过程,你有什么发现?
A
B
C
A′
B′
C′
D
D′
证明:∵△ABC∽△A′B′C′,
∴ ∠B=∠B',
∵AD⊥BC,A'D′⊥B'C',
∴∠ADB=∠A′D′B'=90°.
∴△ABD∽△A'B'D'.
∴ = =k,
∴ = = =kk=k2
如图,△ABC∽△ A'B'C', △ABC与△ A'B'C'的相似比是k,AD、A 'D'是对应高.
相似三角形对应高的比等于相似比.
类似地,相似三角形对应中线、对应角平分线等对应线段的比是否也等于相似比呢?
思考与探索
A
B
C
A′
B′
C′
E
E′
问题1 如图,△ABC∽△ A'B'C', △ABC与△ A'B'C'的相似比是k,AD、A 'D'是对应中线.
=?
证明:∵△ABC∽△A′B′C′,相似比为k.
∴ = =k,∠B=∠B′,
∵AD、A'D'是中线,
∴ =k,
∴ = ,
∴△ABE∽△A′B′E′.
∴ =k.
思考与探索
A
B
C
A′
B′
C′
F
F′
问题2 如图,△ABC∽△ A'B'C', △ABC与△ A'B'C'的相似比是k,AF、A 'F'是角平分线.
=?
证明:∵△ABC∽△A′B′C′,相似比为k.
∴ ∠BAC=∠B′A′C′,∠B=∠B′,
∵AF、A'F'是角平分线,
∴ ∠BAF=∠BAC, ∠B′A′F′=∠B′A′C′,
∴ ∠BAF=∠B′A′F′,
∴△ABF∽△A′B′F′.
∴ =k.
思考与探索
A
B
C
A′
B′
C′
G
G′
问题3 如图,△ABC∽△ A'B'C', △ABC与△ A'B'C'的相似比是k,点G、G′分别在BC、B′C′上,且=k.
=?
证明:∵△ABC∽△A′B′C′,相似比为k.
∴ =k,∠B=∠B′,
∵ =k,
∴ = ,
∴△ABG∽△A′B′G′,
∴ =k.
相似三角形对应中线等于相似比;
相似三角形对应角平分线等于相似比的平方;
类比与归纳
相似三角形对应线段的比等于相似比的平方.
新知巩固
1. 若两个相似三角形对应高的比为1:3,则它们的相似比为______;对应中线的比为______;对应角平分线的比为______;周长的比为______;面积的比为______.
1 : 3
1 : 3
1 : 3
2.已知两个相似三角形的一组对应高分别是15和5,面积之差为80,则较大三角形的面积为________.
90
1 : 3
1 : 9
新知应用
例 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设DE=6,BC=10,GF=5,求点A到DE、BC的距离.
D
B
C
E
G
F
A
┛
解:由DE∥BC,∠AFB= 90°得
∠AGD=90°,即 AG⊥DE.
可知AG、AF的长分别为点A到DE、BC的距离.
∵DE∥BC,
∴∠ADE= ∠B,∠AED=∠C,∴△ADG∽△FEB,
∴,即,
计算,得AG = 7.5,AF= AG+5 = 12.5,
即点A到DE、BC的距离分别为7.5、12.5.
新知巩固
1.如图,点 D、E分别在 AC、AB上,且∠ADE=∠B,F、G分别是 BC、DE的中点. 设 AD= 3,AB= 5,求的值.
解:∵∠ADE=∠B,∠EAD=∠CAB,
∴△EAD∽△CAB.
∵AG、AF分别是△ADE、△ABC的中线,
∴.
E
B
C
D
G
F
A
新知巩固
2. 如图,在△ABC和△A'B'C'中,AD、A'D'分别是△ABC、△A'B'C' 的角平分线,且AB=2A'B',AC=2A'C',∠BAC=∠B'A'C' 求:
(1)的值;(2)△ABC与△A'B'C'的面积的比.
A
B
C
A′
B′
C′
D
D′
解:(1)∵AB=2A'B',AC=2A'C',
∴2,
∵∠BAC=∠B'A'C' ,
∴△BAC∽△B'A'C' ,
∵AD、A'D'分别是△ABC、△A'B'C' 的角平分线,
∴2.
(2)△ABC与△A'B'C'的面积的比为4.
3. 如图,在△ABC中,AB=AC,正方形DEFG的顶点D、G分别在 AB、AC 上,EF在BC上. 设AB=5,BC=6,求正方形DEFG的边长.
新知巩固
A
B
C
D
G
E
F
M
N
解:设正方形DEFG的边长为x,
作△ABC的高AM,AM交DG于点N.
∵AB=AC,BC=6,
∴BM=CM=BC=×6=3,
∵AM⊥BC,
∴ ∠AMB=90°,
在Rt△AMB中,由勾股定理得AM===4.
∵DG∥BC,
∴△ADG∽△ABC.
∴,
∴,解得x=2.4.
类比归纳
全等三角形与相似三角形性质比较:
全等三角形 相似三角形
对应边( ) 对应边的比等于( )
对应角( ) 对应角( )
周长( ) 周长的比等于( )
面积( ) 面积的比等于( )
对应高( ) 对应高的比等于( )
对应中线( ) 对应中线的比等于( )
对应角平分线( ) 对应角平分线的比等于( )
相等
相等
相等
相等
相等
相等
相等
相等
相似比
相似比
相似比
相似比的平方
相似比
相似比
课堂小结
相似三角形中
对应线段的性质
相似三角形对应中线等于相似比;
相似三角形对应角平分线等于相似比的平方;
相似三角形对应线段的比等于相似比的平方.
当堂检测
1. 用一放大镜看一个直角三角形,该三角形的边长放大到原来的10倍后,下列结论错误的 ( )
A.斜边上的中线是原来的10倍 B.斜边上的高是原来的10倍
C.周长是原来的10倍 D.最小内角是原来的10倍
2. 顺次连接三角形三边的中点,所得的三角形与原三角形对应高的比是( )
A.1:4 B.1:3 C.1: D.1:2
D
D
当堂检测
3. 已知△ABC∽△DEF,面积比为9:4,则△ABC与△DEF的对应角平分线之比为( )A. 4:9 B. 9:4 C. 2:3 D. 3:2
D
4. 在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,AP、DQ 是中线,若 AP=2,则 DQ的值为 ( )
A.2 B.4 C.1 D.
C
当堂检测
5. △ABC 与 △A'B'C' 的面积之比是9:25,若 BC 边上的高 AD=12cm,则 B'C' 边上的高 A'D' =_______ .
20 cm
6. 在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为________.
15.5
B
C
A
D
B
C
A
D(A)
E
F
当堂检测
7.如图,在△ABC中,AD是高,点E、F分别在AB、AC上,且EF∥BC,
EF交AD于点G,. 求:
(1)的值;(2)△AEF与△ABC的面积的比.
E
F
B
C
A
G
D
解:(1)∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠C.
∴△AEF∽△ABC.
∵AG、AD分别是△AEF、△ABC的高,
∴ .
(2)∵△AEF∽△ABC,
∴ .
当堂检测
8. 如图,在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC 上,QM 在 BC上,AD交PN于点 E.设BC = 48,AD=16,PQ:PN=5:9,求矩形PQMN的面积.
A
B
C
P
N
Q
E
D
M
解:∵PN∥BC,
∴∠APN=∠B,∠ANP=∠C.
∴△APN∽△ABC.
∵AE、AD分别是△APN、△ABC的高,
∴ .
即 ,解得PQ=10,PN=PQ=18,
∴矩形PQMN的面积=180.
当堂检测
C
A
B
D
E
9.如图,在四边形ABCD中,点E在AD上,且EC∥AB,EB∥DC.
(1)△ABE与△ECD相似吗?为什么?
(2)设△ABE的边BE上的高为h1,△ECD的边CD上的高为h2,△ABE的面积为3,△ECD的面积为1,求的值以及△BCE的面积.
解:(1)由EC// AB ,EB//DC,得∠A=∠CED,∠AEB=∠D.
∴△ABE∽△ECD.
(2)由题意,得==.
又由EB// DC,得△BCE的边BE上的高与△ECD 的边 CD 上的高相等,
∴ =,
=.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
