23.2 中心对称 同步讲练(含解析)
图片预览


文档简介
23.2 中心对称
1. 中心对称的定义
中心对称:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心。
注意以下几点:
中心对称指的就是两个图形的位置关系;只有一个对称中心;绕对称中心旋转180°两个图形能够完全重合。
作一个图形关于某点对称的图形
要作出一个图形关于某一点的成中心对称的图形,关键就是作出该图形上关键点关于对称中心的对称点。最后将对称点按照原图形的形状连接起来,即可的出成中心对称图形。
中心对称的性质
(1)关于中心对称的两个图形上的对应点的连线都经过对称中心,并且都被对称中心平分;
(2)关于中心对称的两个图形能够互相重合,就是全等形;
(3)关于中心对称的两个图形,对应线段平行(或共线)且相等。
题型一、 中心对称的概念及性质
【例1.1】如图,与关于点O成中心对称,下列结论中不成立的是( )
A. B. C.点A的对称点是点 D.
【变式1.1】如图是一个中心对称图形,A为对称中心,若,,,则的长为( )
A.4 B. C. D.
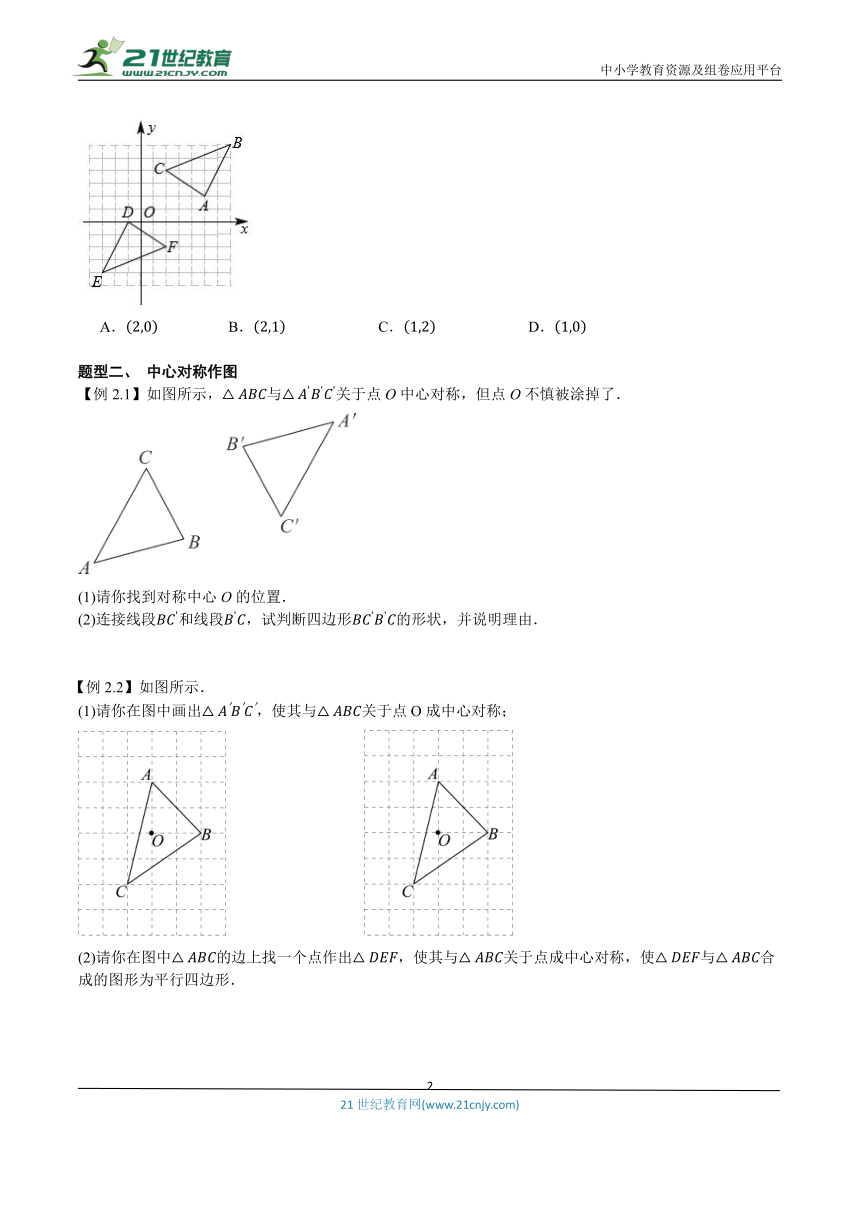
【变式1.2】如图,在平面直角坐标系中,画关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是,请你找出此时的对称中心是( )
A. B. C. D.
题型二、 中心对称作图
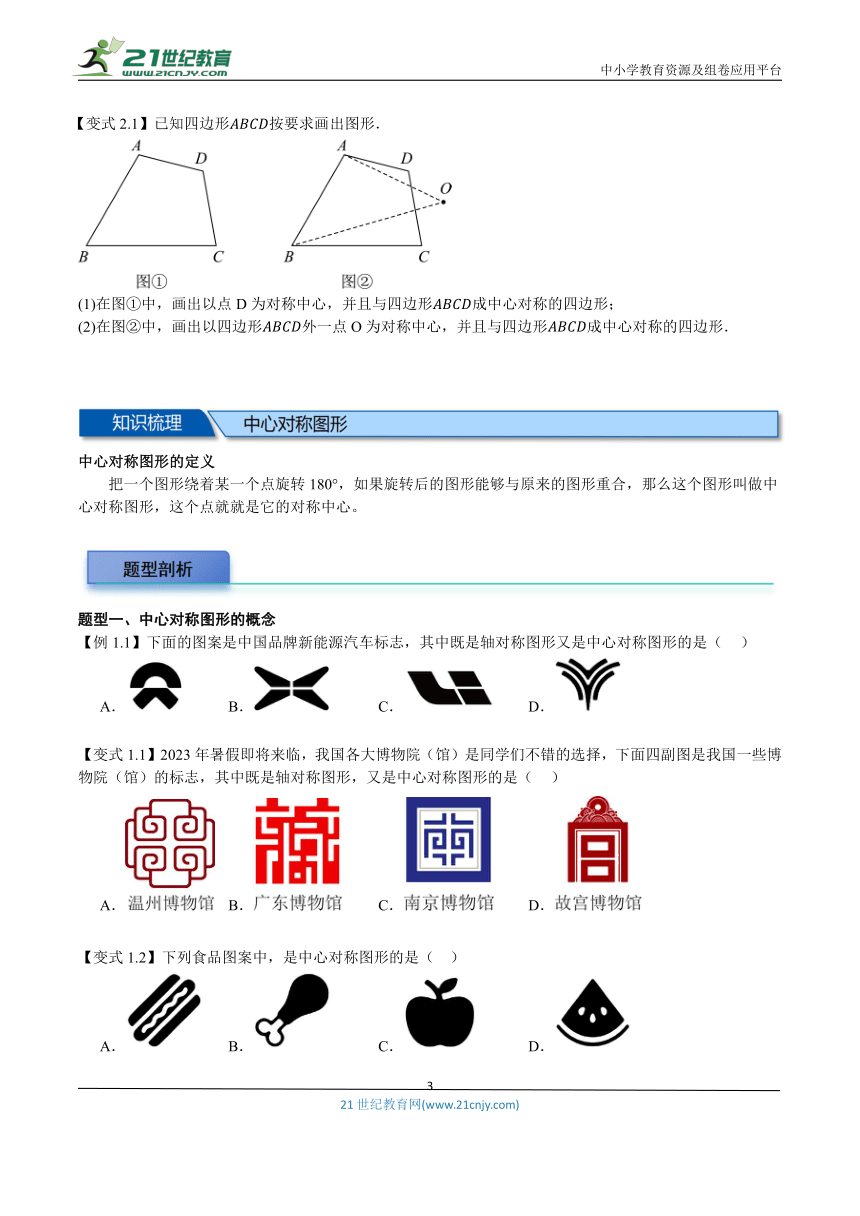
【例2.1】如图所示,与关于点O中心对称,但点O不慎被涂掉了.
(1)请你找到对称中心O的位置.
(2)连接线段和线段,试判断四边形的形状,并说明理由.
【例2.2】如图所示.
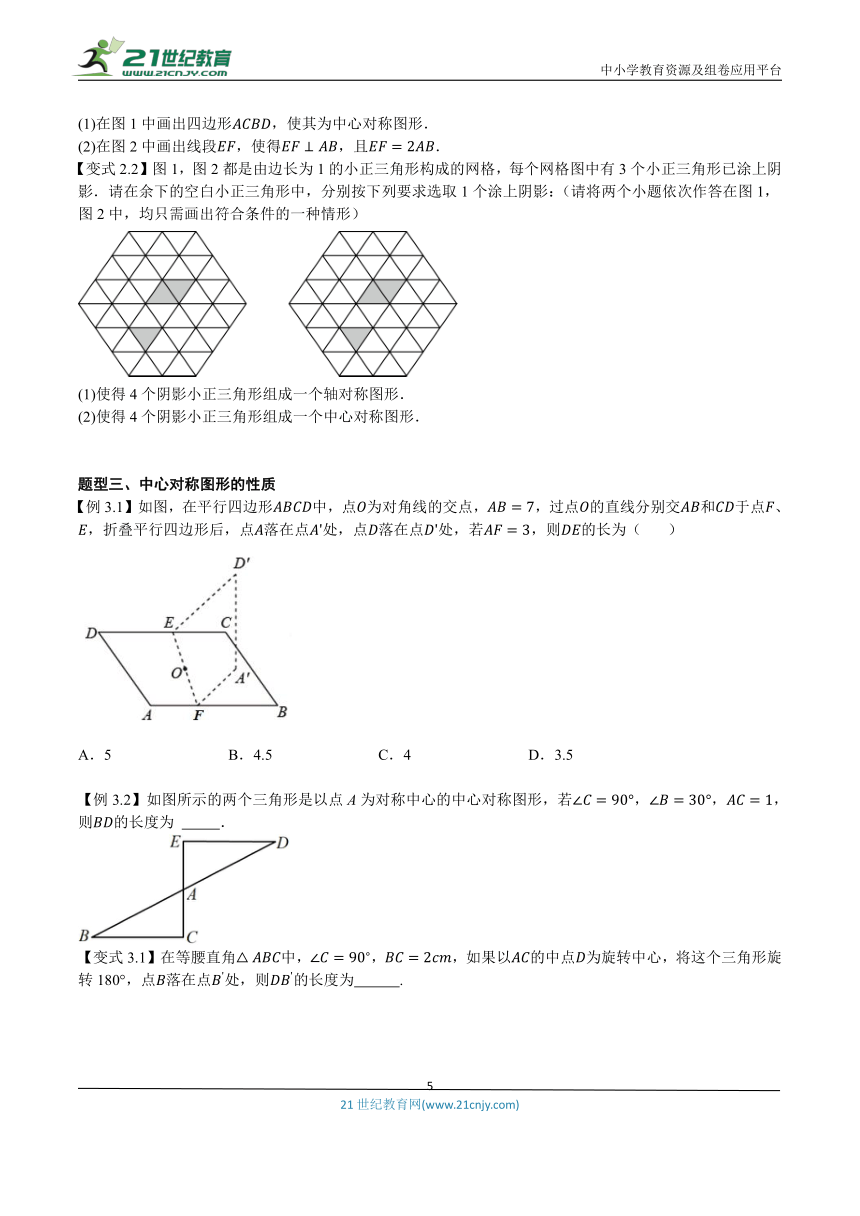
(1)请你在图中画出,使其与关于点O成中心对称;
(2)请你在图中的边上找一个点作出,使其与关于点成中心对称,使与合成的图形为平行四边形.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
【变式2.1】已知四边形按要求画出图形.
(1)在图①中,画出以点D为对称中心,并且与四边形成中心对称的四边形;
(2)在图②中,画出以四边形外一点O为对称中心,并且与四边形成中心对称的四边形.
中心对称图形的定义
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就就是它的对称中心。
题型一、中心对称图形的概念
【例1.1】下面的图案是中国品牌新能源汽车标志,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【变式1.1】2023年暑假即将来临,我国各大博物院(馆)是同学们不错的选择,下面四副图是我国一些博物院(馆)的标志,其中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【变式1.2】下列食品图案中,是中心对称图形的是( )
A. B. C. D.
【变式1.3】下列标志中,是中心对称图形的是( )
A. B.
C. D.
题型二、作中心对称图形
【例2.1】将边长为2的正方形剪成四个全等的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上).
【例2.2】如图是由3个同样的正方形所组成,请再补上一个同样的正方形,使得由4个正方形组成的图形成为一个中心对称图形.画出所有情况(给出的图形不一定全用,不够可添加).
【变式2.1】如图,的正方形网格图中(每个正方形边长为1),已知A、B两点均为格点,连接,请按要求画格点图形(项点均在格点上).
(1)在图1中画出四边形,使其为中心对称图形.
(2)在图2中画出线段,使得,且.
【变式2.2】图1,图2都是由边长为1的小正三角形构成的网格,每个网格图中有3个小正三角形已涂上阴影.请在余下的空白小正三角形中,分别按下列要求选取1个涂上阴影:(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
(1)使得4个阴影小正三角形组成一个轴对称图形.
(2)使得4个阴影小正三角形组成一个中心对称图形.
题型三、中心对称图形的性质
【例3.1】如图,在平行四边形中,点为对角线的交点,,过点的直线分别交和于点、,折叠平行四边形后,点落在点处,点落在点处,若,则的长为( )
A.5 B.4.5 C.4 D.3.5
【例3.2】如图所示的两个三角形是以点A为对称中心的中心对称图形,若,,,则的长度为 .
【变式3.1】在等腰直角中,,,如果以的中点为旋转中心,将这个三角形旋转180°,点落在点处,则的长度为 .
【变式3.2】如图,△ABC与△DBE关于点B成中心对称,若∠A=90°,∠ADC=30°,DE=2,则AB的长为 .
【变式3.3】如图,△ABC和△DEF关于点O中心对称,若OB=4,则OE的长为 .
关于原点对称的点的坐标
在平面直角坐标系中,如果两个点关于原点对称,它们的坐标符号相反,即点p(x,y)关于原点对称点为(-x,-y)。
题型一、关于原点对称的点的坐标
【例1.1】若点与点关于坐标原点成中心对称,则点的坐标是 .
【变式1.1】若点与点关于原点对称,则 .
【变式1.2】平面直角坐标系内与点关于原点对称的点的坐标是,则 .
【变式1.3】已知平行四边形的两条对角线相交于平面直角坐标系中的原点O,点,,则点D的坐标为 .
题型二、作已知图形关于原点对称的图形
【例2.1】如图,平面直角坐标系中, 的顶点坐标分别为,,.
(1)请在图中作出与关于原点对称的图形;
(2)点的坐标是________;点的坐标是________.
【例2.2】如图,正三角形在第一象限内.
(1)作出关于轴为对称轴的对称图形;
(2)作出关于原点为对称中心的对称图形;
(3)与存在怎样的对称关系?
【变式2.1】如图,在平面直角坐标系中,的三个顶点分别为,,.(每个方格的边长均为1个单位长度)
(1)平移得到,若的坐标为,则的坐标为______;
(2)若和关于原点O成中心对称,则的坐标为______;
(3)的面积为______;
(4)将绕点O逆时针旋转,画出旋转后得到的.
【变式2.2】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,的顶点均在格点上.
(1)画出将关于原点O的中心对称图形;
(2)将绕点E逆时针旋转得到,画出.
1.下列航天图标中,其图案是中心对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,点关于原点的对称点为,则的值为( )
A.8 B. C.32 D.
3.下列图形中,是中心对称图形但不一定是轴对称图形的是( )
A.扇形 B.平行四边形 C.等边三角形 D.矩形
4.如图,与关于某个点成中心对称,则这个点是( )
A.点D B.点E C.点F D.点G
5.如图所示的图形中,都是由左边变成右边的图形,分别进行了平移、旋转、轴对称和中心对称变换.其中进行了中心对称变换的是 ,进行了轴对称变换的是 .(填序号)
6.点与点关于原点对称,则的值为 .
7.如图,在平面直角坐标系中,经过中心对称变换得到,那么对称中心的坐标为 .
8.如图,在中,,,,D是的中点,点B,E关于点D成中心对称,则的长为 .
9.如图,与关于C点成中心对称,若,,,求的长
10.如图,和关于点成中心对称.
(1)找出它们的对称中心;
(2)若,,,求的周长;
(3)连接,,试判断四边形的形状,并说明理由.
11.已知三个顶点的坐标分别为,,.
(1)作关于点成中心对称的(点的对应点为,点的对应点为);
(2)把向右平移3个单位,作出平移后的(点的对应点为,点的对应点为,点的对应点为);
(3)轴上存在点,使得的值最小,则点的坐标是______
23.2 中心对称
1. 中心对称的定义
中心对称:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心。
注意以下几点:
中心对称指的就是两个图形的位置关系;只有一个对称中心;绕对称中心旋转180°两个图形能够完全重合。
作一个图形关于某点对称的图形
要作出一个图形关于某一点的成中心对称的图形,关键就是作出该图形上关键点关于对称中心的对称点。最后将对称点按照原图形的形状连接起来,即可的出成中心对称图形。
中心对称的性质
(1)关于中心对称的两个图形上的对应点的连线都经过对称中心,并且都被对称中心平分;
(2)关于中心对称的两个图形能够互相重合,就是全等形;
(3)关于中心对称的两个图形,对应线段平行(或共线)且相等。
题型一、 中心对称的概念及性质
【例1.1】如图,与关于点O成中心对称,下列结论中不成立的是( )
A. B. C.点A的对称点是点 D.
【答案】B
【详解】根据中心对称的性质解决问题即可.
解:∵与关于点O成中心对称,
∴,,点A的对称点是点,,
故A,C,D正确,
故选:B.
【点睛】本题考查中心对称,解题的关键是掌握中心对称的性质,属于中考常考题型.
【变式1.1】如图是一个中心对称图形,A为对称中心,若,,,则的长为( )
A.4 B. C. D.
【答案】A
【分析】在直角中根据30度角所对的直角边等于斜边的一半求得,而,据此即可求解.
【详解】解:在中,,,
,
.
故选:A.
【变式1.2】如图,在平面直角坐标系中,画关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是,请你找出此时的对称中心是( )
A. B. C. D.
【答案】B
【分析】分别求出点的坐标,从而可得的中点坐标,由此即可得.
【详解】解:由图可知,,
的中点坐标为,即为,
的中点坐标为,即为,
的中点坐标为,即为,
的中点坐标均为,
与的对称中心是,
故选:B.
题型二、 中心对称作图
【例2.1】如图所示,与关于点O中心对称,但点O不慎被涂掉了.
(1)请你找到对称中心O的位置.
(2)连接线段和线段,试判断四边形的形状,并说明理由.
【答案】(1)见解析
(2)四边形是平行四边形,理由见解析
【分析】(1)两个图形成中心对称,对应点的连线经过对称中心,且被对称中心平分;连接对应点、,根据对应点的连线经过对称中心,则交点就是对称中心点O;
(2)由中心对称的性质可知:,,再利用平行四边形的判定,即可解决问题.
【详解】(1)解:如图所示:
(2)四边形是平行四边形
由中心对称的性质可得,,
∴四边形是平行四边形.
【例2.2】如图所示.
(1)请你在图中画出,使其与关于点O成中心对称;
(2)请你在图中的边上找一个点作出,使其与关于点成中心对称,使与合成的图形为平行四边形.
【答案】(1)见解析;
(2)见解析;
【分析】(1)将三角形三个顶点分别中心对称后,直接连线即可;
(2)取格点,作平行四边形,可知是对角线中点,则即所求点;或取格点,作平行四边形,可知是对角线中点,则即所求点.
【详解】(1)解:如图所示,即为所求.
(2)解:如图所示,取格点,使得四边形是平行四边形,连接
由图可知,四边形即为所求平行四边形,
则是对角线中点,对角线交点即为所求点.
或取格点,使得四边形是平行四边形,连接,
由图可知,四边形即为所求平行四边形,
则是对角线中点,对角线交点即为所求点.
【点睛】此题考查中心对称,解题关键是图形的中心对称可转化为点的中心对称.
【变式2.1】已知四边形按要求画出图形.
(1)在图①中,画出以点D为对称中心,并且与四边形成中心对称的四边形;
(2)在图②中,画出以四边形外一点O为对称中心,并且与四边形成中心对称的四边形.
【答案】(1)见解析
(2)见解析
【分析】(1)直接利用关于点对称图形的性质得出A,B,C对应点位置进而得出答案.
(2)直接利用关于点对称图形的性质得出A,B,C,D对应点位置进而得出答案.
【详解】(1)解:如图,四边形即为所求;
(2)如图,四边形即为所求.
中心对称图形的定义
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就就是它的对称中心。
题型一、中心对称图形的概念
【例1.1】下面的图案是中国品牌新能源汽车标志,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【答案】B
【分析】根据轴对称图形与中心对称图形的概念求解,如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴,如果一个图形绕某一点旋转后能够与自身重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
【详解】解:、该图形不是中心对称图形,是轴对称图形,故此选项不合题意;
、该图形既是中心对称图形,也是轴对称图形,故此选项符合题意;
、该图形既不是中心对称图形,也不是轴对称图形,故此选项不合题意;
、该图形不是中心对称图形,是轴对称图形,故此选项不合题意.
故选:.
【点睛】本题考查了轴对称图形和中心对称图形的概念,熟练掌握如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴,如果一个图形绕某一点旋转后能够与自身重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心,是解答本题的关键.
【变式1.1】2023年暑假即将来临,我国各大博物院(馆)是同学们不错的选择,下面四副图是我国一些博物院(馆)的标志,其中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【答案】A
【分析】轴对称图形:沿一条直线折叠后,直线两旁的部分能够完全重合;中心对称图形:绕着一个点旋转180°,旋转后的图形能与原来的图形重合.
【详解】解:A:既是轴对称图形,又是中心对称图形,故符合题意;
B:既不是轴对称图形,也不是中心对称图形,故不符合题意;
C:是轴对称图形,不是中心对称图形,故不符合题意;
D:是轴对称图形,不是中心对称图形,故不符合题意;
故选:A
【点睛】本题考查轴对称图形和中心对称图形的识别.掌握相关定义是解题关键.
【变式1.2】下列食品图案中,是中心对称图形的是( )
A. B. C. D.
【答案】A
【分析】根据中心对称图形的概念判断.
【详解】根据中心对称图形定义
即寻找对称中心,旋转后与原图重合
得A符合题意,B、C、D均不符合题意.
故选A.
【点睛】本题考查中心对称图形的概念,中心对称图形是要寻找对称中心,旋转后与原图重合.
【变式1.3】下列标志中,是中心对称图形的是( )
A. B.
C. D.
【答案】B
【分析】根据中心对称图形的定义即可解答.
【详解】解:A、不是中心对称图形,故此选项错误;
B、是中心对称图形,故此选项正确;
C、不是中心对称图形,故此选项错误;
D、不是中心对称图形,故此选项错误;
故选B.
题型二、作中心对称图形
【例2.1】将边长为2的正方形剪成四个全等的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上).
【答案】见解析(答案不唯一,符合题意即可)
【分析】根据轴对称图形和中心对称图形的性质进行作图即可.
【详解】解:①要求是轴对称图形但不是中心对称图形,则可作等腰梯形,如图四边形即为所求;
②要求是中心对称图形但不是轴对称图形,则可作一般平行四边形,如图四边形即为所求;
③要求既是轴对称图形又是中心对称图形,则可作菱形、矩形等,如图四边形即为所求;
④要求既不是轴对称图形又不是中心对称图形,则考虑作任意四边形,如图四边形即为所求.
【点睛】本题考查轴对称图形和中心对称图形的概念及作图,轴对称图形:把一个图形沿着某条直线折叠,能够与另一个图形重合;中心对称图形:把一个图形绕着某个点旋转能够和原图形重合.
【例2.2】如图是由3个同样的正方形所组成,请再补上一个同样的正方形,使得由4个正方形组成的图形成为一个中心对称图形.画出所有情况(给出的图形不一定全用,不够可添加).
【答案】见解析
【分析】根据中心对称图形的概念求解即可.中心对称图形:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.
【详解】解:如图所示,一共有三种情况:
【点睛】此题考查了画中心对称图形,解题的关键是熟练掌握中心对称图形的概念.中心对称图形:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.
【变式2.1】如图,的正方形网格图中(每个正方形边长为1),已知A、B两点均为格点,连接,请按要求画格点图形(项点均在格点上).
(1)在图1中画出四边形,使其为中心对称图形.
(2)在图2中画出线段,使得,且.
【答案】(1)见解析
(2)见解析
【分析】(1)根据中心对称图形的概念求解即可;
(2)根据题意和表格的特点求解即可.
【详解】(1)如图所示,四边形即为所求作四边形.
(2)如图所示,即为所求.
【点睛】本题考查作图-中心对称,垂直等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
【变式2.2】图1,图2都是由边长为1的小正三角形构成的网格,每个网格图中有3个小正三角形已涂上阴影.请在余下的空白小正三角形中,分别按下列要求选取1个涂上阴影:(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
(1)使得4个阴影小正三角形组成一个轴对称图形.
(2)使得4个阴影小正三角形组成一个中心对称图形.
【答案】(1)见解析
(2)见解析
【分析】(1)根据轴对称的性质画出图形即可求解.
(2)根据中心对称的性质画出图象即可求解.
【详解】(1)解:如图所示,答案不唯一,画出一种即可.
(2)如图所示,答案不唯一,画出一种即可.
题型三、中心对称图形的性质
【例3.1】如图,在平行四边形中,点为对角线的交点,,过点的直线分别交和于点、,折叠平行四边形后,点落在点处,点落在点处,若,则的长为( )
A.5 B.4.5 C.4 D.3.5
【答案】C
【分析】根据平行四边形是中心对称图形,对称中心为对角线的交点,则,再根据平行线四边形的性质,可知,继而即可求得
【详解】平行四边形是中心对称图形,对称中心为对角线的交点,根据题意,则
则点和点关于中心对称
,
四边形是平行四边形,
,
,
故选C.
【例3.2】如图所示的两个三角形是以点A为对称中心的中心对称图形,若,,,则的长度为 .
【答案】4
【分析】根据题意得是直角三角形,根据,,可求得,而,据此即可求解.
【详解】解:∵,
∴是直角三角形,
∵,,
∴,
∵所示的两个三角形是以点A为对称中心的中心对称图形,
∴,
故答案为:4.
【点晴】本题主要考查了直角三角形的性质,中心对称图形的性质,解题的关键是掌握这些知识点.
【变式3.1】在等腰直角中,,,如果以的中点为旋转中心,将这个三角形旋转180°,点落在点处,则的长度为 .
【答案】cm
【分析】在Rt△DBC中利用勾股定理即可求得DB的长度,DB′=DB,据此即可求解.
【详解】如图:
在直角△DBC中,则
则
故答案为
【点睛】考查旋转的性质以及勾股定理,画出图形,数形结合是解题的关键.
【变式3.2】如图,△ABC与△DBE关于点B成中心对称,若∠A=90°,∠ADC=30°,DE=2,则AB的长为 .
【答案】
【分析】由中心对称的性质推出,得到,,由锐角的正切求出AD的长,即可求出AB的长.
【详解】解:∵与关于点B成中心对称,
∴,
∴,,
∵,,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查中心对称,直角三角形的性质,勾股定理,解题的关键是掌握中心对称的性质.
【变式3.3】如图,△ABC和△DEF关于点O中心对称,若OB=4,则OE的长为 .
【答案】4
【分析】利用中心对称图形的性质解决问题即可.
【详解】解:∵△ABC和△DEF关于点O中心对称,
∴点B与点E关于点O中心对称,
∴OB=OE,
∵OB=4,
∴OE=4,
故答案为:4.
关于原点对称的点的坐标
在平面直角坐标系中,如果两个点关于原点对称,它们的坐标符号相反,即点p(x,y)关于原点对称点为(-x,-y)。
题型一、关于原点对称的点的坐标
【例1.1】若点与点关于坐标原点成中心对称,则点的坐标是 .
【答案】
【分析】根据点关于原点成中心对称的点的坐标为求解即可.
【详解】解:∵点P与点关于原点成中心对称,
∴点P坐标是,
故答案为:.
【点睛】本题考查关于原点对称的点的坐标,熟练掌握关于原点对称的点的坐标变化规则是解答的关键.
【变式1.1】若点与点关于原点对称,则 .
【答案】
【分析】根据关于原点对称的点的特征:横纵坐标都互为相反数,求出的值,再进行求解即可.
【详解】解:∵点与点关于原点对称,
∴,
∴;
故答案为:9.
【点睛】本题考查关于原点对称的点的特征.解题的关键是掌握关于原点对称的点的特征:横纵坐标都互为相反数.
【变式1.2】平面直角坐标系内与点关于原点对称的点的坐标是,则 .
【答案】
【分析】直接利用关于原点对称点的性质得出x,y的值即可答案.
【详解】解:与点关于原点对称的点的坐标是:.
∴
∴,
故答案为:.
【点睛】此题主要考查了关于点对称点的性质,正确记忆横纵坐标的符号是解题关键.
【变式1.3】已知平行四边形的两条对角线相交于平面直角坐标系中的原点O,点,,则点D的坐标为 .
【答案】
【分析】因为平行四边形两条对角线相互平分,所以点A与点C、点B与点D关于原点对称,由于已知点A,B的坐标,故可求得C,D的坐标.
【详解】解:由题意知:点A与点C、点B与点D关于原点对称,
∵点A,B的坐标分别为,,
∴点C,D的坐标分别是,,
故答案为:.
【点睛】本题考查平行四边形的性质,解题的关键是掌握关于原点对称的点的特征,已知点,则其关于原点对称的点的坐标为.
题型二、作已知图形关于原点对称的图形
【例2.1】如图,平面直角坐标系中, 的顶点坐标分别为,,.
(1)请在图中作出与关于原点对称的图形;
(2)点的坐标是________;点的坐标是________.
【答案】(1)见解析
(2),
【分析】(1)先作出点A和点B关于原点的对称点,再依次连接即可得到;
(2)根据关于原点对称的点横坐标和纵坐标都互为相反数,即可进行解答.
【详解】(1)解:如图所示:即为所求;
(2)解:∵,,
∴,,
故答案为:,.
【点睛】本题主要考查了关于作原点对称的图形,以及关于原点对称点的点坐标特征,解题的关键是掌握关于原点对称的点横坐标和纵坐标都互为相反数.
【例2.2】如图,正三角形在第一象限内.
(1)作出关于轴为对称轴的对称图形;
(2)作出关于原点为对称中心的对称图形;
(3)与存在怎样的对称关系?
【答案】(1)见解析
(2)见解析
(3)关于轴对称
【分析】(1)作A、B、C三点关于x轴的对应点,再顺次连接即可;
(2)作A、B、C三点关于原点的对应点,再顺次连接即可;
(3)由图易得,两个三角形关于y轴对称.
【详解】(1)如图:
即为所求;
(2)如上图,即为所求;
(3)由图可知,与关于轴对称.
【点睛】本题考查了作简单图形轴对称后的图形,其依据是轴对称的性质.基本做法:①先确定图形的关键点;②利用轴对称性质作出关键点的对称;③按原图形中的方式顺次连接对称点.
【变式2.1】如图,在平面直角坐标系中,的三个顶点分别为,,.(每个方格的边长均为1个单位长度)
(1)平移得到,若的坐标为,则的坐标为______;
(2)若和关于原点O成中心对称,则的坐标为______;
(3)的面积为______;
(4)将绕点O逆时针旋转,画出旋转后得到的.
【答案】(1)
(2)
(3)
(4)见解析
【分析】(1)由题意可知,是向右平移3个单位长度,向下平移2个单位长度得到,由此可得答案;
(2)根据中心对称的性质可得答案;
(3)利用割补法求三角形的面积即可;
(4)根据旋转的性质作图即可.
【详解】(1)解:∵,,
∴是向右平移3个单位长度,向下平移2个单位长度得到,
∵,∴的坐标为.
故答案为:;
(2)解:∵和关于原点O成中心对称,,
∴的坐标为.
故答案为:;
(3)解:的面积为,
的面积为.
故答案为:;
(4)解:如图,即为所求.
【变式2.2】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,的顶点均在格点上.
(1)画出将关于原点O的中心对称图形;
(2)将绕点E逆时针旋转得到,画出.
【答案】(1)见解析
(2)见解析
【分析】(1)根据成中心对称图形的性质画图即可;
(2)根据旋转中心、旋转角、旋转方向画图即可.
【详解】(1)作图如下:
(2)作图如下:
1.下列航天图标中,其图案是中心对称图形的是( )
A. B. C. D.
【答案】B
【分析】根据中心对称图形的定义(在平面内,把一个图形绕某点旋转,如果旋转后的图形与另一个图形重合,那么这两个图形互为中心对称图形)逐项判断即可得.
【详解】解: A、不是中心对称图形,故此选项不符合题意;
B、是中心对称图形,故此选项符合题意;
C、不是中心对称图形,故此选项不符合题意;
D、不是中心对称图形,故此选项不符合题意;
故选:B.
2.在平面直角坐标系中,点关于原点的对称点为,则的值为( )
A.8 B. C.32 D.
【答案】B
【分析】根据关于原点对称的点的坐标特点:横纵坐标互为相反数,求出a,b的值,进而可得出结论.
【详解】解:∵点关于原点的对称点为,
,,
∴,
∴.
故选:B.
3.下列图形中,是中心对称图形但不一定是轴对称图形的是( )
A.扇形 B.平行四边形 C.等边三角形 D.矩形
【答案】B
【分析】根据轴对称图形与中心对称图形的概念求解.
【详解】解:A. 扇形,是轴对称图形,不是中心对称图形,故该选项不符合题意;
B. 平行四边形,是中心对称图形但不一定是轴对称图形,故该选项符合题意;
C. 等边三角形,是轴对称图形,不是中心对称图形,故该选项不符合题意;
D. 矩形,是中心对称图形又是轴对称图形,故该选项不符合题意;
故选:B.
4.如图,与关于某个点成中心对称,则这个点是( )
A.点D B.点E C.点F D.点G
【答案】B
【分析】两组对应点连线的交点即是对称中心,根据对称中心的确定方法即可解答.
【详解】如解图,连接、,相交于点E,则点E是对称中心.
故选:B.
5.如图所示的图形中,都是由左边变成右边的图形,分别进行了平移、旋转、轴对称和中心对称变换.其中进行了中心对称变换的是 ,进行了轴对称变换的是 .(填序号)
【答案】 ② ③
【分析】根据中心对称和轴对称的定义即可解答.
【详解】如果一个图形绕着一个定点旋转,如果它能与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,分析可得,进行中心对称变换的是②;
把一个图形沿一条直线对折,如果它能与另一个图形重合,称这两个图形为轴对称,分析可得,则进行轴对称变换的是③;
故答案为:②;③.
【点睛】本题考查了中心对称和轴对称的定义,熟练掌握中心对称和轴对称的定义是解题关键.
6.点与点关于原点对称,则的值为 .
【答案】
【分析】关于原点对称的点,横坐标与纵坐标都互为相反数.
【详解】解:由题意,得,
解得,,
故答案为:.
7.如图,在平面直角坐标系中,经过中心对称变换得到,那么对称中心的坐标为 .
【答案】
【分析】对应点连线的中点即时对称中心的坐标,以此来求解即可.
【详解】解:的中点坐标是,
故答案是:.
【点睛】本题考查了中心对称变换,掌握根据对应点找出对称中心的方法是求解的关键.
8.如图,在中,,,,D是的中点,点B,E关于点D成中心对称,则的长为 .
【答案】6
【分析】先根据勾股定理求出,再根据中心对称的性质可得,最后证明即可求解.
【详解】解:∵,,,
∴,
∵点B,E关于点D成中心对称,
∴,
∵D是的中点,
∴
在和中,
,
∴,
∴,
故答案为:6.
9.如图,与关于C点成中心对称,若,,,求的长
【答案】
【分析】根据与关于C点成中心对称,可得,即可得,,,进而有,在中,利用勾股定理即可求解.
【详解】∵与关于C点成中心对称,
∴,
∴,,,
∵,,,
∴,,,
∴,
∴在中,有:.
即.
【点睛】本题考查了中心对称图形的性质,全等的性质,勾股定理等知识,根据与关于C点成中心对称,得到,是解答本题的关键.
10.如图,和关于点成中心对称.
(1)找出它们的对称中心;
(2)若,,,求的周长;
(3)连接,,试判断四边形的形状,并说明理由.
【答案】(1)见解析
(2)15
(3)平行四边形,理由见解析
【分析】(1)根据中心对称的性质,对称中心在线段AD、CF上,则连接AD和CF,它们的交点即为对称中心O;
(2)根据中心对称的两个三角形全等可得到△DEF各边的长,然后计算△DEF的周长;
(3)根据中心对称的性质得OA=OD,OC=OF,则根据平行四边形的判定方法可判断四边形ACDF为平行四边形.
【详解】(1)如图,点O为所作:
(2)∵△ABC和△DEF关于点O成中心对称,
∴△ABC≌△DEF,
∴DF=AC=6,DE=AB=5,EF=BC=4,
∴△DEF的周长=4+5+6=15;
(3)四边形ACDF为平行四边形.理由如下:
∵△ABC和△DEF关于点O成中心对称,
∴OA=OD,OC=OF,
∴四边形ACDF为平行四边形.
11.已知三个顶点的坐标分别为,,.
(1)作关于点成中心对称的(点的对应点为,点的对应点为);
(2)把向右平移3个单位,作出平移后的(点的对应点为,点的对应点为,点的对应点为);
(3)轴上存在点,使得的值最小,则点的坐标是______
【答案】(1)见解析
(2)见解析
(3)
【分析】(1)分别找到点关于点B对称的点,连接即可;
(2)将各个顶点向右平移三个单位得到对应点,,,连接即可;
(3)利用“将军饮马”模型求解即可
【详解】(1)如图所示,即为所求;
(2)如图所示,即为所求;
(3)如图,找到点关于y轴的对称点,连接,交y轴于点P,根据“将军饮马”模型则点P即为所求,使得的值最小;
由图可知:点,点,点,
设直线,将点,代入解析式得:
,
解得:,
,
故点的坐标为:,
故答案为:
1. 中心对称的定义
中心对称:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心。
注意以下几点:
中心对称指的就是两个图形的位置关系;只有一个对称中心;绕对称中心旋转180°两个图形能够完全重合。
作一个图形关于某点对称的图形
要作出一个图形关于某一点的成中心对称的图形,关键就是作出该图形上关键点关于对称中心的对称点。最后将对称点按照原图形的形状连接起来,即可的出成中心对称图形。
中心对称的性质
(1)关于中心对称的两个图形上的对应点的连线都经过对称中心,并且都被对称中心平分;
(2)关于中心对称的两个图形能够互相重合,就是全等形;
(3)关于中心对称的两个图形,对应线段平行(或共线)且相等。
题型一、 中心对称的概念及性质
【例1.1】如图,与关于点O成中心对称,下列结论中不成立的是( )
A. B. C.点A的对称点是点 D.
【变式1.1】如图是一个中心对称图形,A为对称中心,若,,,则的长为( )
A.4 B. C. D.
【变式1.2】如图,在平面直角坐标系中,画关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是,请你找出此时的对称中心是( )
A. B. C. D.
题型二、 中心对称作图
【例2.1】如图所示,与关于点O中心对称,但点O不慎被涂掉了.
(1)请你找到对称中心O的位置.
(2)连接线段和线段,试判断四边形的形状,并说明理由.
【例2.2】如图所示.
(1)请你在图中画出,使其与关于点O成中心对称;
(2)请你在图中的边上找一个点作出,使其与关于点成中心对称,使与合成的图形为平行四边形.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
【变式2.1】已知四边形按要求画出图形.
(1)在图①中,画出以点D为对称中心,并且与四边形成中心对称的四边形;
(2)在图②中,画出以四边形外一点O为对称中心,并且与四边形成中心对称的四边形.
中心对称图形的定义
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就就是它的对称中心。
题型一、中心对称图形的概念
【例1.1】下面的图案是中国品牌新能源汽车标志,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【变式1.1】2023年暑假即将来临,我国各大博物院(馆)是同学们不错的选择,下面四副图是我国一些博物院(馆)的标志,其中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【变式1.2】下列食品图案中,是中心对称图形的是( )
A. B. C. D.
【变式1.3】下列标志中,是中心对称图形的是( )
A. B.
C. D.
题型二、作中心对称图形
【例2.1】将边长为2的正方形剪成四个全等的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上).
【例2.2】如图是由3个同样的正方形所组成,请再补上一个同样的正方形,使得由4个正方形组成的图形成为一个中心对称图形.画出所有情况(给出的图形不一定全用,不够可添加).
【变式2.1】如图,的正方形网格图中(每个正方形边长为1),已知A、B两点均为格点,连接,请按要求画格点图形(项点均在格点上).
(1)在图1中画出四边形,使其为中心对称图形.
(2)在图2中画出线段,使得,且.
【变式2.2】图1,图2都是由边长为1的小正三角形构成的网格,每个网格图中有3个小正三角形已涂上阴影.请在余下的空白小正三角形中,分别按下列要求选取1个涂上阴影:(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
(1)使得4个阴影小正三角形组成一个轴对称图形.
(2)使得4个阴影小正三角形组成一个中心对称图形.
题型三、中心对称图形的性质
【例3.1】如图,在平行四边形中,点为对角线的交点,,过点的直线分别交和于点、,折叠平行四边形后,点落在点处,点落在点处,若,则的长为( )
A.5 B.4.5 C.4 D.3.5
【例3.2】如图所示的两个三角形是以点A为对称中心的中心对称图形,若,,,则的长度为 .
【变式3.1】在等腰直角中,,,如果以的中点为旋转中心,将这个三角形旋转180°,点落在点处,则的长度为 .
【变式3.2】如图,△ABC与△DBE关于点B成中心对称,若∠A=90°,∠ADC=30°,DE=2,则AB的长为 .
【变式3.3】如图,△ABC和△DEF关于点O中心对称,若OB=4,则OE的长为 .
关于原点对称的点的坐标
在平面直角坐标系中,如果两个点关于原点对称,它们的坐标符号相反,即点p(x,y)关于原点对称点为(-x,-y)。
题型一、关于原点对称的点的坐标
【例1.1】若点与点关于坐标原点成中心对称,则点的坐标是 .
【变式1.1】若点与点关于原点对称,则 .
【变式1.2】平面直角坐标系内与点关于原点对称的点的坐标是,则 .
【变式1.3】已知平行四边形的两条对角线相交于平面直角坐标系中的原点O,点,,则点D的坐标为 .
题型二、作已知图形关于原点对称的图形
【例2.1】如图,平面直角坐标系中, 的顶点坐标分别为,,.
(1)请在图中作出与关于原点对称的图形;
(2)点的坐标是________;点的坐标是________.
【例2.2】如图,正三角形在第一象限内.
(1)作出关于轴为对称轴的对称图形;
(2)作出关于原点为对称中心的对称图形;
(3)与存在怎样的对称关系?
【变式2.1】如图,在平面直角坐标系中,的三个顶点分别为,,.(每个方格的边长均为1个单位长度)
(1)平移得到,若的坐标为,则的坐标为______;
(2)若和关于原点O成中心对称,则的坐标为______;
(3)的面积为______;
(4)将绕点O逆时针旋转,画出旋转后得到的.
【变式2.2】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,的顶点均在格点上.
(1)画出将关于原点O的中心对称图形;
(2)将绕点E逆时针旋转得到,画出.
1.下列航天图标中,其图案是中心对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,点关于原点的对称点为,则的值为( )
A.8 B. C.32 D.
3.下列图形中,是中心对称图形但不一定是轴对称图形的是( )
A.扇形 B.平行四边形 C.等边三角形 D.矩形
4.如图,与关于某个点成中心对称,则这个点是( )
A.点D B.点E C.点F D.点G
5.如图所示的图形中,都是由左边变成右边的图形,分别进行了平移、旋转、轴对称和中心对称变换.其中进行了中心对称变换的是 ,进行了轴对称变换的是 .(填序号)
6.点与点关于原点对称,则的值为 .
7.如图,在平面直角坐标系中,经过中心对称变换得到,那么对称中心的坐标为 .
8.如图,在中,,,,D是的中点,点B,E关于点D成中心对称,则的长为 .
9.如图,与关于C点成中心对称,若,,,求的长
10.如图,和关于点成中心对称.
(1)找出它们的对称中心;
(2)若,,,求的周长;
(3)连接,,试判断四边形的形状,并说明理由.
11.已知三个顶点的坐标分别为,,.
(1)作关于点成中心对称的(点的对应点为,点的对应点为);
(2)把向右平移3个单位,作出平移后的(点的对应点为,点的对应点为,点的对应点为);
(3)轴上存在点,使得的值最小,则点的坐标是______
23.2 中心对称
1. 中心对称的定义
中心对称:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心。
注意以下几点:
中心对称指的就是两个图形的位置关系;只有一个对称中心;绕对称中心旋转180°两个图形能够完全重合。
作一个图形关于某点对称的图形
要作出一个图形关于某一点的成中心对称的图形,关键就是作出该图形上关键点关于对称中心的对称点。最后将对称点按照原图形的形状连接起来,即可的出成中心对称图形。
中心对称的性质
(1)关于中心对称的两个图形上的对应点的连线都经过对称中心,并且都被对称中心平分;
(2)关于中心对称的两个图形能够互相重合,就是全等形;
(3)关于中心对称的两个图形,对应线段平行(或共线)且相等。
题型一、 中心对称的概念及性质
【例1.1】如图,与关于点O成中心对称,下列结论中不成立的是( )
A. B. C.点A的对称点是点 D.
【答案】B
【详解】根据中心对称的性质解决问题即可.
解:∵与关于点O成中心对称,
∴,,点A的对称点是点,,
故A,C,D正确,
故选:B.
【点睛】本题考查中心对称,解题的关键是掌握中心对称的性质,属于中考常考题型.
【变式1.1】如图是一个中心对称图形,A为对称中心,若,,,则的长为( )
A.4 B. C. D.
【答案】A
【分析】在直角中根据30度角所对的直角边等于斜边的一半求得,而,据此即可求解.
【详解】解:在中,,,
,
.
故选:A.
【变式1.2】如图,在平面直角坐标系中,画关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是,请你找出此时的对称中心是( )
A. B. C. D.
【答案】B
【分析】分别求出点的坐标,从而可得的中点坐标,由此即可得.
【详解】解:由图可知,,
的中点坐标为,即为,
的中点坐标为,即为,
的中点坐标为,即为,
的中点坐标均为,
与的对称中心是,
故选:B.
题型二、 中心对称作图
【例2.1】如图所示,与关于点O中心对称,但点O不慎被涂掉了.
(1)请你找到对称中心O的位置.
(2)连接线段和线段,试判断四边形的形状,并说明理由.
【答案】(1)见解析
(2)四边形是平行四边形,理由见解析
【分析】(1)两个图形成中心对称,对应点的连线经过对称中心,且被对称中心平分;连接对应点、,根据对应点的连线经过对称中心,则交点就是对称中心点O;
(2)由中心对称的性质可知:,,再利用平行四边形的判定,即可解决问题.
【详解】(1)解:如图所示:
(2)四边形是平行四边形
由中心对称的性质可得,,
∴四边形是平行四边形.
【例2.2】如图所示.
(1)请你在图中画出,使其与关于点O成中心对称;
(2)请你在图中的边上找一个点作出,使其与关于点成中心对称,使与合成的图形为平行四边形.
【答案】(1)见解析;
(2)见解析;
【分析】(1)将三角形三个顶点分别中心对称后,直接连线即可;
(2)取格点,作平行四边形,可知是对角线中点,则即所求点;或取格点,作平行四边形,可知是对角线中点,则即所求点.
【详解】(1)解:如图所示,即为所求.
(2)解:如图所示,取格点,使得四边形是平行四边形,连接
由图可知,四边形即为所求平行四边形,
则是对角线中点,对角线交点即为所求点.
或取格点,使得四边形是平行四边形,连接,
由图可知,四边形即为所求平行四边形,
则是对角线中点,对角线交点即为所求点.
【点睛】此题考查中心对称,解题关键是图形的中心对称可转化为点的中心对称.
【变式2.1】已知四边形按要求画出图形.
(1)在图①中,画出以点D为对称中心,并且与四边形成中心对称的四边形;
(2)在图②中,画出以四边形外一点O为对称中心,并且与四边形成中心对称的四边形.
【答案】(1)见解析
(2)见解析
【分析】(1)直接利用关于点对称图形的性质得出A,B,C对应点位置进而得出答案.
(2)直接利用关于点对称图形的性质得出A,B,C,D对应点位置进而得出答案.
【详解】(1)解:如图,四边形即为所求;
(2)如图,四边形即为所求.
中心对称图形的定义
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就就是它的对称中心。
题型一、中心对称图形的概念
【例1.1】下面的图案是中国品牌新能源汽车标志,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【答案】B
【分析】根据轴对称图形与中心对称图形的概念求解,如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴,如果一个图形绕某一点旋转后能够与自身重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
【详解】解:、该图形不是中心对称图形,是轴对称图形,故此选项不合题意;
、该图形既是中心对称图形,也是轴对称图形,故此选项符合题意;
、该图形既不是中心对称图形,也不是轴对称图形,故此选项不合题意;
、该图形不是中心对称图形,是轴对称图形,故此选项不合题意.
故选:.
【点睛】本题考查了轴对称图形和中心对称图形的概念,熟练掌握如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴,如果一个图形绕某一点旋转后能够与自身重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心,是解答本题的关键.
【变式1.1】2023年暑假即将来临,我国各大博物院(馆)是同学们不错的选择,下面四副图是我国一些博物院(馆)的标志,其中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【答案】A
【分析】轴对称图形:沿一条直线折叠后,直线两旁的部分能够完全重合;中心对称图形:绕着一个点旋转180°,旋转后的图形能与原来的图形重合.
【详解】解:A:既是轴对称图形,又是中心对称图形,故符合题意;
B:既不是轴对称图形,也不是中心对称图形,故不符合题意;
C:是轴对称图形,不是中心对称图形,故不符合题意;
D:是轴对称图形,不是中心对称图形,故不符合题意;
故选:A
【点睛】本题考查轴对称图形和中心对称图形的识别.掌握相关定义是解题关键.
【变式1.2】下列食品图案中,是中心对称图形的是( )
A. B. C. D.
【答案】A
【分析】根据中心对称图形的概念判断.
【详解】根据中心对称图形定义
即寻找对称中心,旋转后与原图重合
得A符合题意,B、C、D均不符合题意.
故选A.
【点睛】本题考查中心对称图形的概念,中心对称图形是要寻找对称中心,旋转后与原图重合.
【变式1.3】下列标志中,是中心对称图形的是( )
A. B.
C. D.
【答案】B
【分析】根据中心对称图形的定义即可解答.
【详解】解:A、不是中心对称图形,故此选项错误;
B、是中心对称图形,故此选项正确;
C、不是中心对称图形,故此选项错误;
D、不是中心对称图形,故此选项错误;
故选B.
题型二、作中心对称图形
【例2.1】将边长为2的正方形剪成四个全等的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上).
【答案】见解析(答案不唯一,符合题意即可)
【分析】根据轴对称图形和中心对称图形的性质进行作图即可.
【详解】解:①要求是轴对称图形但不是中心对称图形,则可作等腰梯形,如图四边形即为所求;
②要求是中心对称图形但不是轴对称图形,则可作一般平行四边形,如图四边形即为所求;
③要求既是轴对称图形又是中心对称图形,则可作菱形、矩形等,如图四边形即为所求;
④要求既不是轴对称图形又不是中心对称图形,则考虑作任意四边形,如图四边形即为所求.
【点睛】本题考查轴对称图形和中心对称图形的概念及作图,轴对称图形:把一个图形沿着某条直线折叠,能够与另一个图形重合;中心对称图形:把一个图形绕着某个点旋转能够和原图形重合.
【例2.2】如图是由3个同样的正方形所组成,请再补上一个同样的正方形,使得由4个正方形组成的图形成为一个中心对称图形.画出所有情况(给出的图形不一定全用,不够可添加).
【答案】见解析
【分析】根据中心对称图形的概念求解即可.中心对称图形:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.
【详解】解:如图所示,一共有三种情况:
【点睛】此题考查了画中心对称图形,解题的关键是熟练掌握中心对称图形的概念.中心对称图形:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.
【变式2.1】如图,的正方形网格图中(每个正方形边长为1),已知A、B两点均为格点,连接,请按要求画格点图形(项点均在格点上).
(1)在图1中画出四边形,使其为中心对称图形.
(2)在图2中画出线段,使得,且.
【答案】(1)见解析
(2)见解析
【分析】(1)根据中心对称图形的概念求解即可;
(2)根据题意和表格的特点求解即可.
【详解】(1)如图所示,四边形即为所求作四边形.
(2)如图所示,即为所求.
【点睛】本题考查作图-中心对称,垂直等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
【变式2.2】图1,图2都是由边长为1的小正三角形构成的网格,每个网格图中有3个小正三角形已涂上阴影.请在余下的空白小正三角形中,分别按下列要求选取1个涂上阴影:(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
(1)使得4个阴影小正三角形组成一个轴对称图形.
(2)使得4个阴影小正三角形组成一个中心对称图形.
【答案】(1)见解析
(2)见解析
【分析】(1)根据轴对称的性质画出图形即可求解.
(2)根据中心对称的性质画出图象即可求解.
【详解】(1)解:如图所示,答案不唯一,画出一种即可.
(2)如图所示,答案不唯一,画出一种即可.
题型三、中心对称图形的性质
【例3.1】如图,在平行四边形中,点为对角线的交点,,过点的直线分别交和于点、,折叠平行四边形后,点落在点处,点落在点处,若,则的长为( )
A.5 B.4.5 C.4 D.3.5
【答案】C
【分析】根据平行四边形是中心对称图形,对称中心为对角线的交点,则,再根据平行线四边形的性质,可知,继而即可求得
【详解】平行四边形是中心对称图形,对称中心为对角线的交点,根据题意,则
则点和点关于中心对称
,
四边形是平行四边形,
,
,
故选C.
【例3.2】如图所示的两个三角形是以点A为对称中心的中心对称图形,若,,,则的长度为 .
【答案】4
【分析】根据题意得是直角三角形,根据,,可求得,而,据此即可求解.
【详解】解:∵,
∴是直角三角形,
∵,,
∴,
∵所示的两个三角形是以点A为对称中心的中心对称图形,
∴,
故答案为:4.
【点晴】本题主要考查了直角三角形的性质,中心对称图形的性质,解题的关键是掌握这些知识点.
【变式3.1】在等腰直角中,,,如果以的中点为旋转中心,将这个三角形旋转180°,点落在点处,则的长度为 .
【答案】cm
【分析】在Rt△DBC中利用勾股定理即可求得DB的长度,DB′=DB,据此即可求解.
【详解】如图:
在直角△DBC中,则
则
故答案为
【点睛】考查旋转的性质以及勾股定理,画出图形,数形结合是解题的关键.
【变式3.2】如图,△ABC与△DBE关于点B成中心对称,若∠A=90°,∠ADC=30°,DE=2,则AB的长为 .
【答案】
【分析】由中心对称的性质推出,得到,,由锐角的正切求出AD的长,即可求出AB的长.
【详解】解:∵与关于点B成中心对称,
∴,
∴,,
∵,,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查中心对称,直角三角形的性质,勾股定理,解题的关键是掌握中心对称的性质.
【变式3.3】如图,△ABC和△DEF关于点O中心对称,若OB=4,则OE的长为 .
【答案】4
【分析】利用中心对称图形的性质解决问题即可.
【详解】解:∵△ABC和△DEF关于点O中心对称,
∴点B与点E关于点O中心对称,
∴OB=OE,
∵OB=4,
∴OE=4,
故答案为:4.
关于原点对称的点的坐标
在平面直角坐标系中,如果两个点关于原点对称,它们的坐标符号相反,即点p(x,y)关于原点对称点为(-x,-y)。
题型一、关于原点对称的点的坐标
【例1.1】若点与点关于坐标原点成中心对称,则点的坐标是 .
【答案】
【分析】根据点关于原点成中心对称的点的坐标为求解即可.
【详解】解:∵点P与点关于原点成中心对称,
∴点P坐标是,
故答案为:.
【点睛】本题考查关于原点对称的点的坐标,熟练掌握关于原点对称的点的坐标变化规则是解答的关键.
【变式1.1】若点与点关于原点对称,则 .
【答案】
【分析】根据关于原点对称的点的特征:横纵坐标都互为相反数,求出的值,再进行求解即可.
【详解】解:∵点与点关于原点对称,
∴,
∴;
故答案为:9.
【点睛】本题考查关于原点对称的点的特征.解题的关键是掌握关于原点对称的点的特征:横纵坐标都互为相反数.
【变式1.2】平面直角坐标系内与点关于原点对称的点的坐标是,则 .
【答案】
【分析】直接利用关于原点对称点的性质得出x,y的值即可答案.
【详解】解:与点关于原点对称的点的坐标是:.
∴
∴,
故答案为:.
【点睛】此题主要考查了关于点对称点的性质,正确记忆横纵坐标的符号是解题关键.
【变式1.3】已知平行四边形的两条对角线相交于平面直角坐标系中的原点O,点,,则点D的坐标为 .
【答案】
【分析】因为平行四边形两条对角线相互平分,所以点A与点C、点B与点D关于原点对称,由于已知点A,B的坐标,故可求得C,D的坐标.
【详解】解:由题意知:点A与点C、点B与点D关于原点对称,
∵点A,B的坐标分别为,,
∴点C,D的坐标分别是,,
故答案为:.
【点睛】本题考查平行四边形的性质,解题的关键是掌握关于原点对称的点的特征,已知点,则其关于原点对称的点的坐标为.
题型二、作已知图形关于原点对称的图形
【例2.1】如图,平面直角坐标系中, 的顶点坐标分别为,,.
(1)请在图中作出与关于原点对称的图形;
(2)点的坐标是________;点的坐标是________.
【答案】(1)见解析
(2),
【分析】(1)先作出点A和点B关于原点的对称点,再依次连接即可得到;
(2)根据关于原点对称的点横坐标和纵坐标都互为相反数,即可进行解答.
【详解】(1)解:如图所示:即为所求;
(2)解:∵,,
∴,,
故答案为:,.
【点睛】本题主要考查了关于作原点对称的图形,以及关于原点对称点的点坐标特征,解题的关键是掌握关于原点对称的点横坐标和纵坐标都互为相反数.
【例2.2】如图,正三角形在第一象限内.
(1)作出关于轴为对称轴的对称图形;
(2)作出关于原点为对称中心的对称图形;
(3)与存在怎样的对称关系?
【答案】(1)见解析
(2)见解析
(3)关于轴对称
【分析】(1)作A、B、C三点关于x轴的对应点,再顺次连接即可;
(2)作A、B、C三点关于原点的对应点,再顺次连接即可;
(3)由图易得,两个三角形关于y轴对称.
【详解】(1)如图:
即为所求;
(2)如上图,即为所求;
(3)由图可知,与关于轴对称.
【点睛】本题考查了作简单图形轴对称后的图形,其依据是轴对称的性质.基本做法:①先确定图形的关键点;②利用轴对称性质作出关键点的对称;③按原图形中的方式顺次连接对称点.
【变式2.1】如图,在平面直角坐标系中,的三个顶点分别为,,.(每个方格的边长均为1个单位长度)
(1)平移得到,若的坐标为,则的坐标为______;
(2)若和关于原点O成中心对称,则的坐标为______;
(3)的面积为______;
(4)将绕点O逆时针旋转,画出旋转后得到的.
【答案】(1)
(2)
(3)
(4)见解析
【分析】(1)由题意可知,是向右平移3个单位长度,向下平移2个单位长度得到,由此可得答案;
(2)根据中心对称的性质可得答案;
(3)利用割补法求三角形的面积即可;
(4)根据旋转的性质作图即可.
【详解】(1)解:∵,,
∴是向右平移3个单位长度,向下平移2个单位长度得到,
∵,∴的坐标为.
故答案为:;
(2)解:∵和关于原点O成中心对称,,
∴的坐标为.
故答案为:;
(3)解:的面积为,
的面积为.
故答案为:;
(4)解:如图,即为所求.
【变式2.2】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,的顶点均在格点上.
(1)画出将关于原点O的中心对称图形;
(2)将绕点E逆时针旋转得到,画出.
【答案】(1)见解析
(2)见解析
【分析】(1)根据成中心对称图形的性质画图即可;
(2)根据旋转中心、旋转角、旋转方向画图即可.
【详解】(1)作图如下:
(2)作图如下:
1.下列航天图标中,其图案是中心对称图形的是( )
A. B. C. D.
【答案】B
【分析】根据中心对称图形的定义(在平面内,把一个图形绕某点旋转,如果旋转后的图形与另一个图形重合,那么这两个图形互为中心对称图形)逐项判断即可得.
【详解】解: A、不是中心对称图形,故此选项不符合题意;
B、是中心对称图形,故此选项符合题意;
C、不是中心对称图形,故此选项不符合题意;
D、不是中心对称图形,故此选项不符合题意;
故选:B.
2.在平面直角坐标系中,点关于原点的对称点为,则的值为( )
A.8 B. C.32 D.
【答案】B
【分析】根据关于原点对称的点的坐标特点:横纵坐标互为相反数,求出a,b的值,进而可得出结论.
【详解】解:∵点关于原点的对称点为,
,,
∴,
∴.
故选:B.
3.下列图形中,是中心对称图形但不一定是轴对称图形的是( )
A.扇形 B.平行四边形 C.等边三角形 D.矩形
【答案】B
【分析】根据轴对称图形与中心对称图形的概念求解.
【详解】解:A. 扇形,是轴对称图形,不是中心对称图形,故该选项不符合题意;
B. 平行四边形,是中心对称图形但不一定是轴对称图形,故该选项符合题意;
C. 等边三角形,是轴对称图形,不是中心对称图形,故该选项不符合题意;
D. 矩形,是中心对称图形又是轴对称图形,故该选项不符合题意;
故选:B.
4.如图,与关于某个点成中心对称,则这个点是( )
A.点D B.点E C.点F D.点G
【答案】B
【分析】两组对应点连线的交点即是对称中心,根据对称中心的确定方法即可解答.
【详解】如解图,连接、,相交于点E,则点E是对称中心.
故选:B.
5.如图所示的图形中,都是由左边变成右边的图形,分别进行了平移、旋转、轴对称和中心对称变换.其中进行了中心对称变换的是 ,进行了轴对称变换的是 .(填序号)
【答案】 ② ③
【分析】根据中心对称和轴对称的定义即可解答.
【详解】如果一个图形绕着一个定点旋转,如果它能与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,分析可得,进行中心对称变换的是②;
把一个图形沿一条直线对折,如果它能与另一个图形重合,称这两个图形为轴对称,分析可得,则进行轴对称变换的是③;
故答案为:②;③.
【点睛】本题考查了中心对称和轴对称的定义,熟练掌握中心对称和轴对称的定义是解题关键.
6.点与点关于原点对称,则的值为 .
【答案】
【分析】关于原点对称的点,横坐标与纵坐标都互为相反数.
【详解】解:由题意,得,
解得,,
故答案为:.
7.如图,在平面直角坐标系中,经过中心对称变换得到,那么对称中心的坐标为 .
【答案】
【分析】对应点连线的中点即时对称中心的坐标,以此来求解即可.
【详解】解:的中点坐标是,
故答案是:.
【点睛】本题考查了中心对称变换,掌握根据对应点找出对称中心的方法是求解的关键.
8.如图,在中,,,,D是的中点,点B,E关于点D成中心对称,则的长为 .
【答案】6
【分析】先根据勾股定理求出,再根据中心对称的性质可得,最后证明即可求解.
【详解】解:∵,,,
∴,
∵点B,E关于点D成中心对称,
∴,
∵D是的中点,
∴
在和中,
,
∴,
∴,
故答案为:6.
9.如图,与关于C点成中心对称,若,,,求的长
【答案】
【分析】根据与关于C点成中心对称,可得,即可得,,,进而有,在中,利用勾股定理即可求解.
【详解】∵与关于C点成中心对称,
∴,
∴,,,
∵,,,
∴,,,
∴,
∴在中,有:.
即.
【点睛】本题考查了中心对称图形的性质,全等的性质,勾股定理等知识,根据与关于C点成中心对称,得到,是解答本题的关键.
10.如图,和关于点成中心对称.
(1)找出它们的对称中心;
(2)若,,,求的周长;
(3)连接,,试判断四边形的形状,并说明理由.
【答案】(1)见解析
(2)15
(3)平行四边形,理由见解析
【分析】(1)根据中心对称的性质,对称中心在线段AD、CF上,则连接AD和CF,它们的交点即为对称中心O;
(2)根据中心对称的两个三角形全等可得到△DEF各边的长,然后计算△DEF的周长;
(3)根据中心对称的性质得OA=OD,OC=OF,则根据平行四边形的判定方法可判断四边形ACDF为平行四边形.
【详解】(1)如图,点O为所作:
(2)∵△ABC和△DEF关于点O成中心对称,
∴△ABC≌△DEF,
∴DF=AC=6,DE=AB=5,EF=BC=4,
∴△DEF的周长=4+5+6=15;
(3)四边形ACDF为平行四边形.理由如下:
∵△ABC和△DEF关于点O成中心对称,
∴OA=OD,OC=OF,
∴四边形ACDF为平行四边形.
11.已知三个顶点的坐标分别为,,.
(1)作关于点成中心对称的(点的对应点为,点的对应点为);
(2)把向右平移3个单位,作出平移后的(点的对应点为,点的对应点为,点的对应点为);
(3)轴上存在点,使得的值最小,则点的坐标是______
【答案】(1)见解析
(2)见解析
(3)
【分析】(1)分别找到点关于点B对称的点,连接即可;
(2)将各个顶点向右平移三个单位得到对应点,,,连接即可;
(3)利用“将军饮马”模型求解即可
【详解】(1)如图所示,即为所求;
(2)如图所示,即为所求;
(3)如图,找到点关于y轴的对称点,连接,交y轴于点P,根据“将军饮马”模型则点P即为所求,使得的值最小;
由图可知:点,点,点,
设直线,将点,代入解析式得:
,
解得:,
,
故点的坐标为:,
故答案为:
同课章节目录
