人教A版(2019)选择性必修第一册2.5.2 圆与圆的位置关系 课件(共29张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册2.5.2 圆与圆的位置关系 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 48.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 12:26:23 | ||
图片预览






文档简介
(共29张PPT)
2.5.2 圆与圆的位置关系
第 二 章 直线和圆的方程
人教A版2019选修第一册
学习目标
1.掌握圆与圆的位置关系及判定方法,培养数学抽象的核心素养;
2.能根据圆的方程判断圆与圆的位置关系,培养数学运算的核心素养;
3.能综合应用圆与圆的位置关系解决问题,培养逻辑推理的核心素养。
01情景导入
PART ONE
情景导入
日食是一种天文现象,在民间称此现象为天狗食日。日食只在月球与太阳呈现合的状态时发生。日食分为日偏食、日全食、日环食、全环食。
我们将月亮与太阳抽象为圆,观察到的这些圆在变化的过程中位置关系是怎样的
前面我们运用直线的方程,圆的方程研究了直线与圆的位置关系,现在我们类比上述研究方法,运用圆的方程,通过定量计算研究圆与圆的位置关系。
02圆与圆的位置关系
PART ONE
圆与圆的位置关系
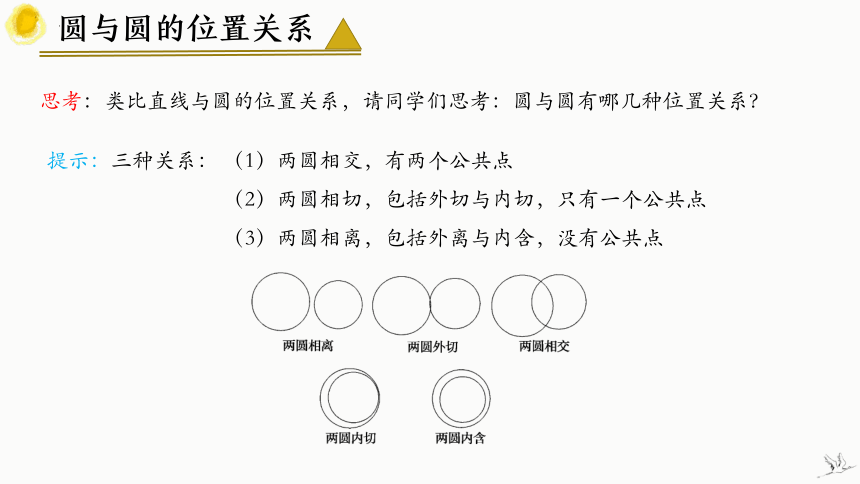
思考:类比直线与圆的位置关系,请同学们思考:圆与圆有哪几种位置关系?
提示:三种关系: (1)两圆相交,有两个公共点
(2)两圆相切,包括外切与内切,只有一个公共点
(3)两圆相离,包括外离与内含,没有公共点
圆与圆的位置关系
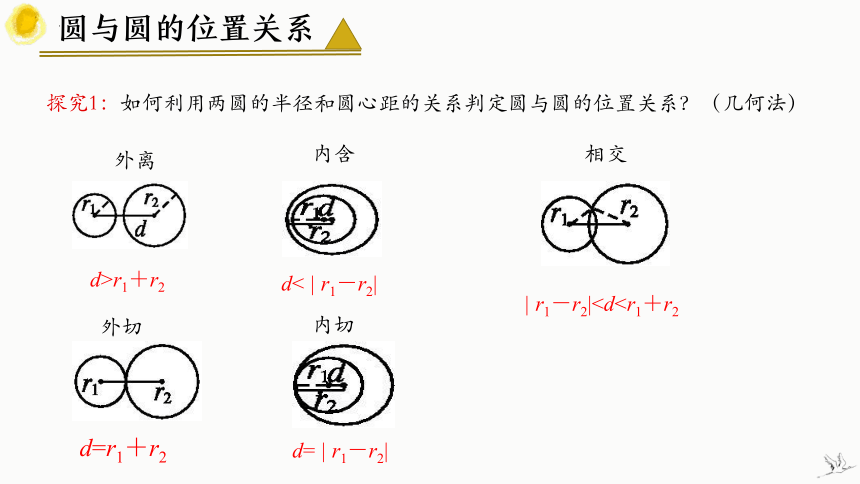
探究1:如何利用两圆的半径和圆心距的关系判定圆与圆的位置关系?(几何法)
d>r1+r2
外离
d< | r1-r2|
内含
相交
外切
内切
d=r1+r2
| r1-r2|d= | r1-r2|
圆与圆的位置关系
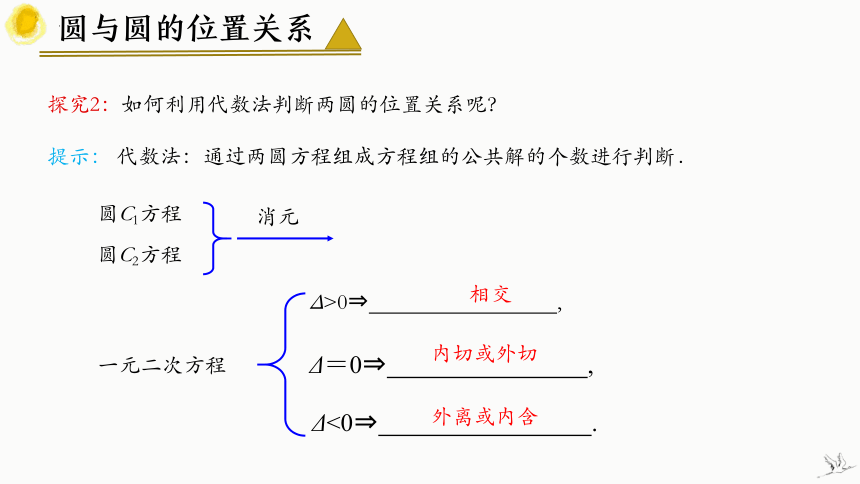
探究2:如何利用代数法判断两圆的位置关系呢?
提示: 代数法:通过两圆方程组成方程组的公共解的个数进行判断.
一元二次方程
圆C1方程
圆C2方程
消元
Δ<0 .
Δ>0 ,
Δ=0 ,
相交
内切或外切
外离或内含
圆与圆的位置关系
例1:已知圆和圆,试判断圆与圆的位置关系.
解法一:圆与圆的方程联立,得
(1)-(2),得
所以,方程(4)有两个不相等的实数根,
所以圆与圆相交,它们有两个公共点.
⑶
圆与圆的位置关系
解法二:
把圆C1和圆C2的方程化为标准方程:
∴ 圆与圆相交,它们有两个公共点.
圆与圆的位置关系
练习. 判断下列两圆的位置关系:
①(x+2)2+(y-2)2=1与(x-2)2+(y-5)2=16.
②x2+y2+6x-7=0与x2+y2+6y-27=0.
解:①根据题意得,两圆的半径分别为r1=1和r2=4,两圆的圆心距
因为d=r1+r2,所以两圆外切.
②将两圆的方程化为标准方程,得(x+3)2+y2=16,x2+(y+3)2=36,
故两圆的半径分别为r1=4和r2=6.
两圆的圆心距
圆与圆的位置关系
例2 已知圆C1:x2+y2-2ax-2y+a2-15=0(a>0),圆C2:x2+y2-4ax-2y+4a2=0(a>0).试求a为何值时,两圆C1,C2的位置关系为:
(1)相切;(2)相交;(3)外离;(4)内含
解:圆C1,C2的方程,经配方后可得
C1:(x-a)2+(y-1)2=16,
C2:(x-2a)2+(y-1)2=1,
∴圆心C1(a,1),C2(2a,1),半径r1=4,r2=1.
(1)当|C1C2|=r1+r2=5,即a=5时,两圆外切;
当|C1C2|=r1-r2=3,即a=3时,两圆内切.
(2)当3<|C1C2|<5,即3(3)当|C1C2|>5,即a>5时,两圆外离.
(4)当|C1C2|<3,即0圆与圆的位置关系
判断两圆的位置关系的两种方法
(1)几何法:利用两圆半径的和或差与圆心距作比较,得到两圆的位置关系;
(2)代数法:把两圆位置关系的判定完全转化为代数问题,转化为方程组的解的组数问题.
方法总结
03相交弦与公切线
PART ONE
相交弦
思考:如何求直线与圆、圆与圆的交点和弦长?
相交弦
相交弦
相交弦
4x+3y-2=0
10
相交弦
例 求圆心在直线x-y-4=0上且经过两圆x2+y2-4x-6=0和x2+y2-4y-6=0的交点的圆的方程.
思路分析 可联立两圆方程求交点坐标,进而求出圆的圆心和半径;也可利用过两圆交点的圆系方程,根据已知条件求出待定系数.
相交弦
相交弦
相交弦
公切线
例 (1)两个圆C1:x2+y2+2x+2y-2=0与C2:x2+y2-4x-2y+1=0的公切线有且仅有( )
A.1条 B.2条 C.3条 D.4条
B
两个圆为外切位置关系,所以公切线有两条
公切线
公切线
公切线
两圆的公切线包括外公切线和内公切线两种.
(1)两圆外离时,有2条外公切线和2条内公切线,共4条;
(2)两圆外切时,有2条外公切线和1条内公切线,共3条;
(3)两圆相交时,只有2条外公切线;
(4)两圆内切时,只有1条外公切线;
(5)两圆内含时,无公切线.
归纳总结
公切线
思路分析:设圆的方程,利用两圆外切和直线与圆相切建立方程组求得.
解:设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),
由题知所求圆与圆x2+y2-2x=0外切,
04课堂小结
PART ONE
课堂小结
2.5.2 圆与圆的位置关系
第 二 章 直线和圆的方程
人教A版2019选修第一册
学习目标
1.掌握圆与圆的位置关系及判定方法,培养数学抽象的核心素养;
2.能根据圆的方程判断圆与圆的位置关系,培养数学运算的核心素养;
3.能综合应用圆与圆的位置关系解决问题,培养逻辑推理的核心素养。
01情景导入
PART ONE
情景导入
日食是一种天文现象,在民间称此现象为天狗食日。日食只在月球与太阳呈现合的状态时发生。日食分为日偏食、日全食、日环食、全环食。
我们将月亮与太阳抽象为圆,观察到的这些圆在变化的过程中位置关系是怎样的
前面我们运用直线的方程,圆的方程研究了直线与圆的位置关系,现在我们类比上述研究方法,运用圆的方程,通过定量计算研究圆与圆的位置关系。
02圆与圆的位置关系
PART ONE
圆与圆的位置关系
思考:类比直线与圆的位置关系,请同学们思考:圆与圆有哪几种位置关系?
提示:三种关系: (1)两圆相交,有两个公共点
(2)两圆相切,包括外切与内切,只有一个公共点
(3)两圆相离,包括外离与内含,没有公共点
圆与圆的位置关系
探究1:如何利用两圆的半径和圆心距的关系判定圆与圆的位置关系?(几何法)
d>r1+r2
外离
d< | r1-r2|
内含
相交
外切
内切
d=r1+r2
| r1-r2|
圆与圆的位置关系
探究2:如何利用代数法判断两圆的位置关系呢?
提示: 代数法:通过两圆方程组成方程组的公共解的个数进行判断.
一元二次方程
圆C1方程
圆C2方程
消元
Δ<0 .
Δ>0 ,
Δ=0 ,
相交
内切或外切
外离或内含
圆与圆的位置关系
例1:已知圆和圆,试判断圆与圆的位置关系.
解法一:圆与圆的方程联立,得
(1)-(2),得
所以,方程(4)有两个不相等的实数根,
所以圆与圆相交,它们有两个公共点.
⑶
圆与圆的位置关系
解法二:
把圆C1和圆C2的方程化为标准方程:
∴ 圆与圆相交,它们有两个公共点.
圆与圆的位置关系
练习. 判断下列两圆的位置关系:
①(x+2)2+(y-2)2=1与(x-2)2+(y-5)2=16.
②x2+y2+6x-7=0与x2+y2+6y-27=0.
解:①根据题意得,两圆的半径分别为r1=1和r2=4,两圆的圆心距
因为d=r1+r2,所以两圆外切.
②将两圆的方程化为标准方程,得(x+3)2+y2=16,x2+(y+3)2=36,
故两圆的半径分别为r1=4和r2=6.
两圆的圆心距
圆与圆的位置关系
例2 已知圆C1:x2+y2-2ax-2y+a2-15=0(a>0),圆C2:x2+y2-4ax-2y+4a2=0(a>0).试求a为何值时,两圆C1,C2的位置关系为:
(1)相切;(2)相交;(3)外离;(4)内含
解:圆C1,C2的方程,经配方后可得
C1:(x-a)2+(y-1)2=16,
C2:(x-2a)2+(y-1)2=1,
∴圆心C1(a,1),C2(2a,1),半径r1=4,r2=1.
(1)当|C1C2|=r1+r2=5,即a=5时,两圆外切;
当|C1C2|=r1-r2=3,即a=3时,两圆内切.
(2)当3<|C1C2|<5,即3
(4)当|C1C2|<3,即0
判断两圆的位置关系的两种方法
(1)几何法:利用两圆半径的和或差与圆心距作比较,得到两圆的位置关系;
(2)代数法:把两圆位置关系的判定完全转化为代数问题,转化为方程组的解的组数问题.
方法总结
03相交弦与公切线
PART ONE
相交弦
思考:如何求直线与圆、圆与圆的交点和弦长?
相交弦
相交弦
相交弦
4x+3y-2=0
10
相交弦
例 求圆心在直线x-y-4=0上且经过两圆x2+y2-4x-6=0和x2+y2-4y-6=0的交点的圆的方程.
思路分析 可联立两圆方程求交点坐标,进而求出圆的圆心和半径;也可利用过两圆交点的圆系方程,根据已知条件求出待定系数.
相交弦
相交弦
相交弦
公切线
例 (1)两个圆C1:x2+y2+2x+2y-2=0与C2:x2+y2-4x-2y+1=0的公切线有且仅有( )
A.1条 B.2条 C.3条 D.4条
B
两个圆为外切位置关系,所以公切线有两条
公切线
公切线
公切线
两圆的公切线包括外公切线和内公切线两种.
(1)两圆外离时,有2条外公切线和2条内公切线,共4条;
(2)两圆外切时,有2条外公切线和1条内公切线,共3条;
(3)两圆相交时,只有2条外公切线;
(4)两圆内切时,只有1条外公切线;
(5)两圆内含时,无公切线.
归纳总结
公切线
思路分析:设圆的方程,利用两圆外切和直线与圆相切建立方程组求得.
解:设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),
由题知所求圆与圆x2+y2-2x=0外切,
04课堂小结
PART ONE
课堂小结
