计算专题一:长方体和正方体(易错专项)数学六年级上册苏教版(含解析)
文档属性
| 名称 | 计算专题一:长方体和正方体(易错专项)数学六年级上册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 17:43:59 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
计算专题一:长方体和正方体(易错专项)数学六年级上册苏教版
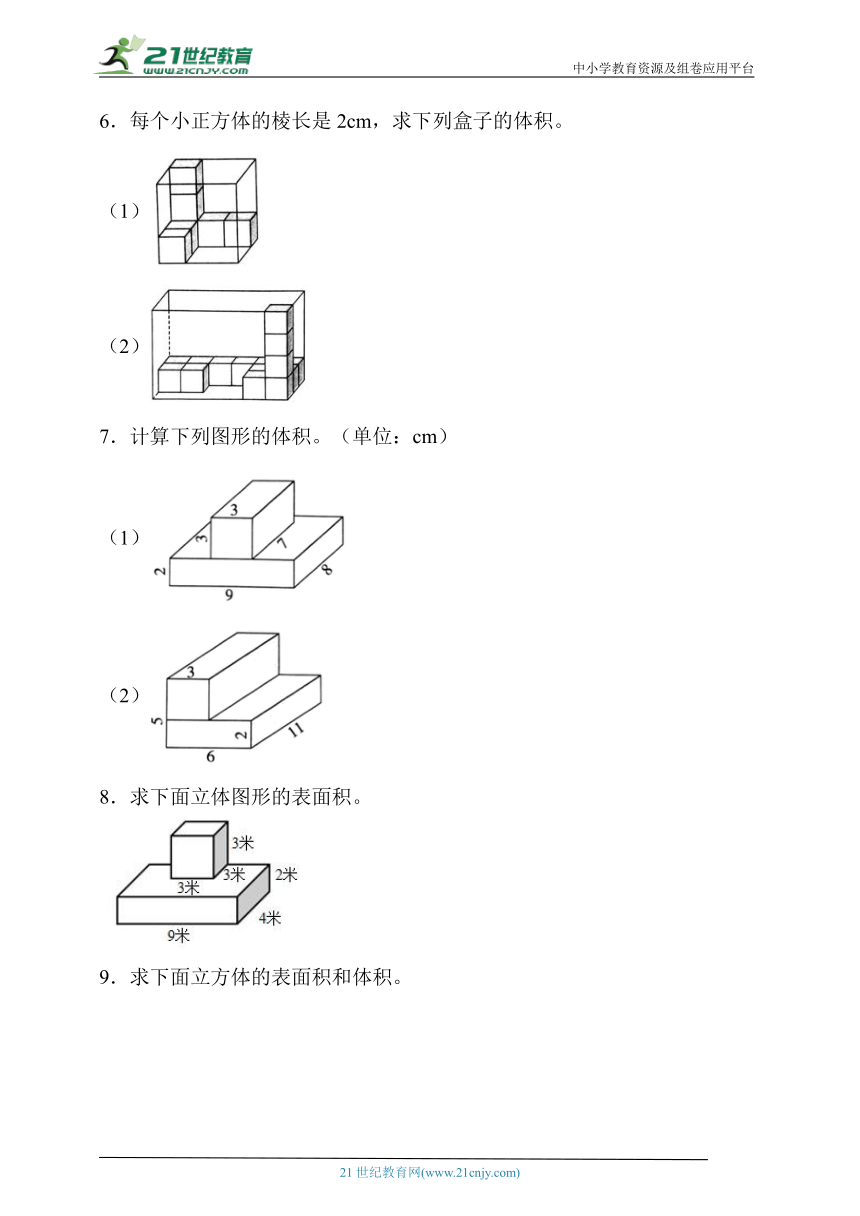
1.求表面积。(单位:cm)
2.下图为棱长6厘米的正方体,求其体积和表面积。
3.求下面图形的体积。(单位:分米)
4.求下列组合体的体积。(单位:分米)
5.求图形的体积。单位:厘米)。
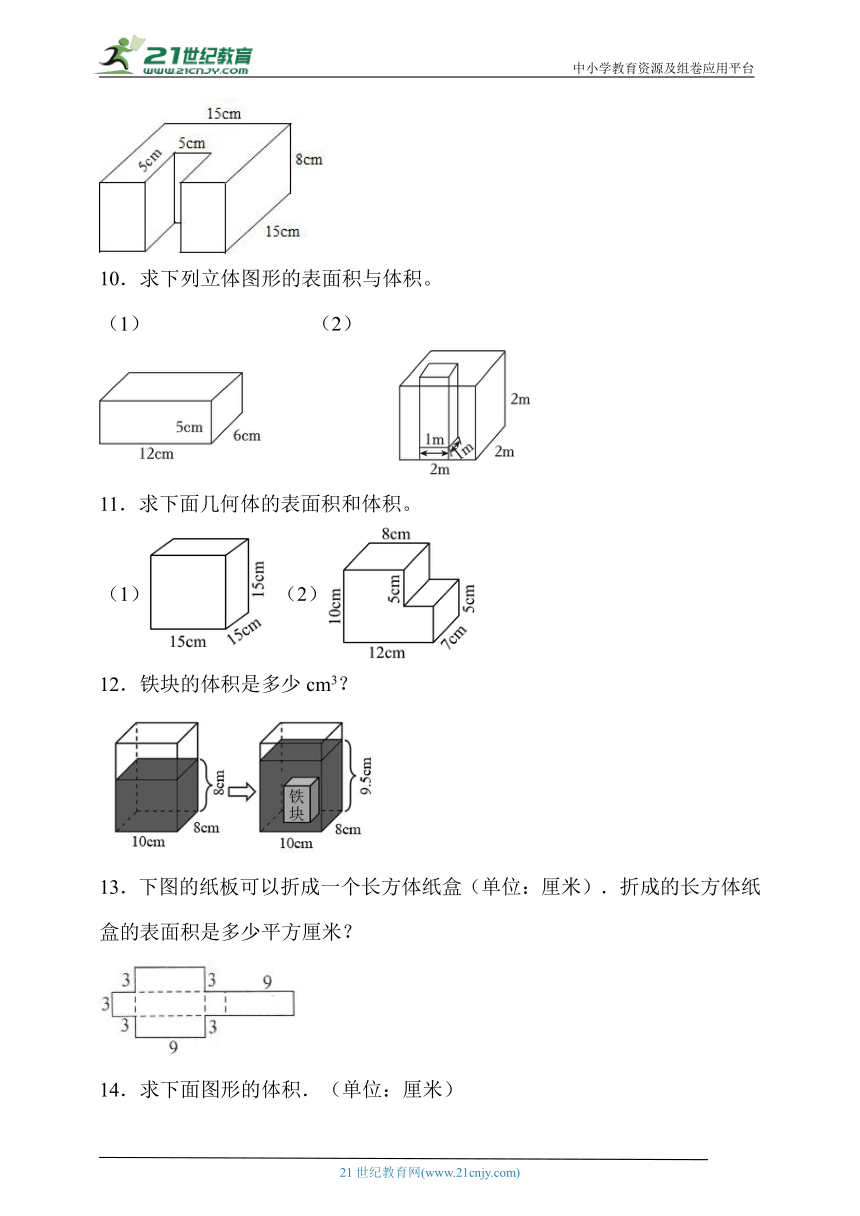
6.每个小正方体的棱长是2cm,求下列盒子的体积。
(1)
(2)
7.计算下列图形的体积。(单位:cm)
(1)
(2)
8.求下面立体图形的表面积。
9.求下面立方体的表面积和体积。
10.求下列立体图形的表面积与体积。
(1) (2)
11.求下面几何体的表面积和体积。
(1) (2)
12.铁块的体积是多少cm3?
13.下图的纸板可以折成一个长方体纸盒(单位:厘米).折成的长方体纸盒的表面积是多少平方厘米?
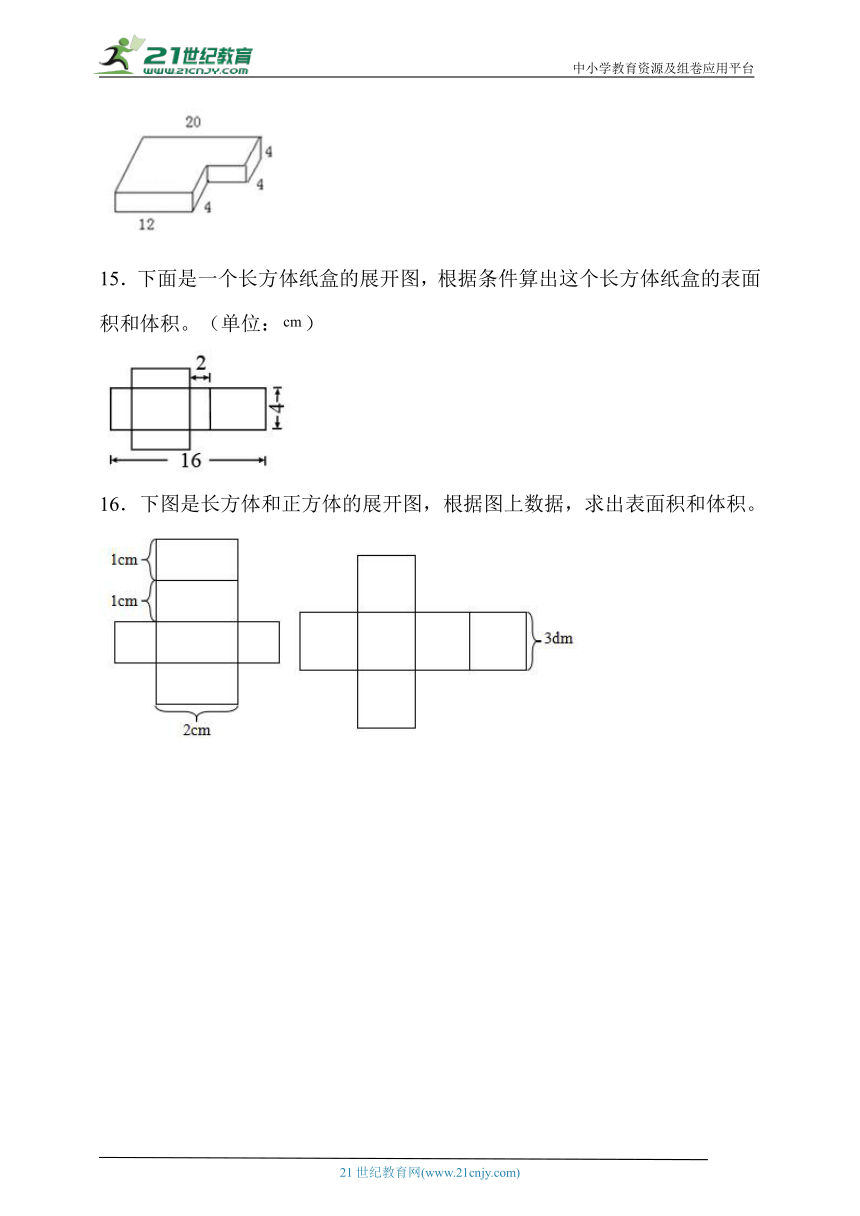
14.求下面图形的体积.(单位:厘米)
15.下面是一个长方体纸盒的展开图,根据条件算出这个长方体纸盒的表面积和体积。(单位:)
16.下图是长方体和正方体的展开图,根据图上数据,求出表面积和体积。
参考答案:
1.236平方厘米
【分析】根据长方体的表面积公式:s=(ab+ah+bh)×2,代入数据计算即可。
【详解】(8×5+8×6+5×6)×2
=(40+48+30)×2
=118×2
=236(平方厘米)
答:表面积是236平方厘米。
【点睛】此题主要考查长方体的表面积的计算,牢记公式是关键。
2.216立方厘米;216平方厘米
【分析】正方体的体积=棱长×棱长×棱长,正方体的表面积=棱长×棱长×6。根据公式代入数据计算即可。
【详解】体积:6×6×6=216(立方厘米)
表面积:6×6×6=216(平方厘米)
【点睛】牢记公式,细心计算,注意单位。
3.13.12立方分米
【分析】观察组合体可知,是由一个长方体减去一个小长方体而成,根据长方体体积公式:长×宽×高即可解答。
【详解】5×0.8×4-[2×(5-1.6-1.6)×0.8]
=16-(2×1.8×0.8)
=16-2.88
=13.12(立方分米)
【点睛】此题主要考查学生的组合图形应用解题方法,需要掌握长方体的体积公式。
4.660立方分米
【分析】观察组合体可知,是由两个长方体拼接而成,根据长方体体积公式:长×宽×高即可解答。
【详解】5×5×12+(8-5)×10×12
=300+360
=660(立方分米)
【点睛】此题主要考查学生对组合图形的应用解题方法,需要掌握长方体的体积公式。
5.13392立方厘米
【分析】根据长方体的体积公式:长×宽×高,即可代数解答。
【详解】(50-16)×14×12+16×12×40
=34×14×12+16×12×40
=5712+7680
=13392(立方厘米)
【点睛】此题主要考查学生的长方体应用解题方法,需要掌握长方体的体积公式:长×宽×高。
6.(1)216立方厘米;(2)576立方厘米
【分析】(1)通过观察图形可知,图1的三条棱长分别等于3个小正方体棱长和,故正方体的棱长为:2×3,然后通过正方体体积公式:棱长×棱长×棱长即可解答;
(2)通过观察图形可知,图2的长=6个小正方体棱长和,故长为:2×6;宽=3个小正方体棱长和,故宽为:2×3;高=4个小正方体棱长和,故高为:2×4;然后通过长方体体积公式:长×宽×高即可解答。
【详解】(1)根据分析可知:棱长为:2×3=6(厘米)
6×6×6
=36×6
=216(立方厘米)
(2)根据分析可知:长:2×6=12(厘米),宽:2×3=6(厘米),高:2×4=8(厘米)
12×6×8
=72×8
=576(立方厘米)
【点睛】此题主要考查学生对正方体和长方体体积公式的理解与解答,同时,也考查了学生的空间想象力。
7.(1)207立方厘米;(2)231立方厘米
【分析】根据长方体体积公式:长×宽×高,分别求出两个长方体体积,然后再加在一起即可求出组合图形体积,即可解答。
【详解】(1)3×3×7+2×9×8
=63+144
=207(立方厘米)
(2)3×(5-2)×11+2×6×11
=99+132
=231(立方厘米)
【点睛】此题主要考查学生对组合图形体积的理解与分析解题能力,需要牢记长方体体积公式,即长×宽×高。
8.160平方米
【分析】将小正方体的上面下移至长方体与正方体接触面,所求面积可以看成一个长方体的表面积和正方体四个面的面积之和。长方体表面积公式:(长×宽+长×高+宽×高)×2;正方体表面积公式:棱长×棱长×6,根据基础公式灵活应用即可。
【详解】
(平方米)
答:立体图形的表面积是160平方米。
【点睛】此题主要考查正方体和长方体组合图形的表面积,需要理解所求面积可以看成一个长方体的表面积和正方体四个面的面积之和。
9.表面积960平方厘米;体积1600立方厘米。
【分析】由图可知此立方体是一个长宽高分别是15cm、15cm、8cm的一个大长方体去掉一个长宽高分别是5cm、5cm、8cm的小长方体的立体图形,立方体的表面积等于大长方体表面积-上下空缺的两个正方形面积+空缺内部左右两个长方形面积;立方体的体积=大长方体的体积-空缺部分小长方体的体积。
【详解】表面积:(15×15+15×8+15×8)×2-5×5×2+5×8×2
=930-50+80
=960(平方厘米)
体积:15×15×8-5×5×8
=1800-200
=1600(立方厘米)
答:立方体的表面积是960平方厘米;体积是1600立方厘米。
【点睛】此题考查组合体的表面积及体积的计算,注意认真观察图形求表面积时不要多加面也不要少减面。
10.(1)324cm2;360cm3
(2)30m2;6m3
【分析】(1)根据长方体表面积公式S=(ab+ah+bh)×2,体积公式V=abh,代入数据计算求解。
(2)组合图形的表面积=正方体表面积-长方体上下面的面积+长方体的侧面积,其中长方体上下面是2个边长为1m的正方形,长方体的侧面是4个相同的长为2m、宽为1m的长方形;根据正方体的表面积公式S=6a2,正方形的面积公式S=a2,长方形的面积公式S=ab;代入数据计算求解;
组合图形的体积=正方体的体积-长方体的体积;根据正方体的体积公式V=a3,长方体的体积公式V=abh,代入数据计算求解。
【详解】(1)表面积:
(12×6+12×5+6×5)×2
=(72+60+30)×2
=162×2
=324(cm2)
体积:
12×6×5=360(cm3)
长方体的表面积是324cm2,体积是360cm3。
(2)表面积:
2×2×6-1×1×2+2×1×4
=24-2+8
=30(m2)
体积:
2×2×2-1×1×2
=8-2
=6(m3)
组合图形的表面积是30m2,体积是6m3。
11.(1)1350平方厘米;3375立方厘米
(2)508平方厘米;700立方厘米
【分析】(1)正方体的表面积=棱长×棱长×6;正方体的体积=棱长×棱长×棱长;
(2)根据题图可将几何体看成一个长为12厘米、宽为7厘米、高为10厘米的长方体,再减去长为5厘米、宽为(12-8)厘米的两个长方形即可;用这个长方体的体积减去长为7厘米、高为5厘米、宽为(12-8)厘米的长方体体积即可。
【详解】(1)15×15×6
=225×6
=1350(平方厘米);
15×15×15
=225×15
=3375(立方厘米);
(2)(12×7+12×10+7×10)×2-(12-8)×5×2
=274×2-40
=508(平方厘米);
(2)12×7×10-7×5×(12-8)
=840-140
=700(立方厘米)
12.120cm3
【分析】水面上升的体积就是铁块的体积,长方体容器的长×宽×上升的水的高度=铁块体积,据此列式计算。
【详解】10×8×(9.5-8)
=80×1.5
=120(cm3)
13.126平方厘米
【详解】略
14.512立方厘米
【详解】12×(4+4)×4+(20-12)×4×4
=12×8×4+128
=384+128
=512(立方厘米),
答:这个组合图形的体积是512立方厘米
15.88平方厘米;48立方厘米
【分析】由题图可知:长方体两个长与两个宽的和是16厘米,据此求出长方体的长,再根据表面积和体积公式解答即可。
【详解】
=8-2
=6(厘米);
=44×2
=88(平方厘米);
体积:
=24×4
=96(立方厘米);
答:长方体纸盒的表面积是88平方厘米,体积是96立方厘米。
【点睛】本题考查根据展开图还原长方体的知识,它的关键是先确定长方体的长、宽、高,再求出长方体的表面积和体积。
16.长方体的表面积:10平方厘米;长方体的体积: 2立方厘米;
正方体的表面积:54平方分米;正方体的体积:27立方分米
【分析】由图意可知:长方体的长、宽、高分别为2厘米、1厘米和1厘米,正方体的棱长是3分米,分别利用长方体的表面积公式S=(ab+bh+ah)×2和长方体的体积公式V=abh,正方体的表面积公式S=6a2和正方体的体积公式V=a3即可求出其表面积和体积。
【详解】长方体的表面积:
(2×1+2×1+1×1)×2
=(2+2+1)×2
=5×2
=10(平方厘米);
长方体的体积:2×1×1=2(立方厘米)
正方体的表面积:
3×3×6
=9×6
=54(平方分米);
正方体的体积:
3×3×3
=9×3
=27(立方分米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
计算专题一:长方体和正方体(易错专项)数学六年级上册苏教版
1.求表面积。(单位:cm)
2.下图为棱长6厘米的正方体,求其体积和表面积。
3.求下面图形的体积。(单位:分米)
4.求下列组合体的体积。(单位:分米)
5.求图形的体积。单位:厘米)。
6.每个小正方体的棱长是2cm,求下列盒子的体积。
(1)
(2)
7.计算下列图形的体积。(单位:cm)
(1)
(2)
8.求下面立体图形的表面积。
9.求下面立方体的表面积和体积。
10.求下列立体图形的表面积与体积。
(1) (2)
11.求下面几何体的表面积和体积。
(1) (2)
12.铁块的体积是多少cm3?
13.下图的纸板可以折成一个长方体纸盒(单位:厘米).折成的长方体纸盒的表面积是多少平方厘米?
14.求下面图形的体积.(单位:厘米)
15.下面是一个长方体纸盒的展开图,根据条件算出这个长方体纸盒的表面积和体积。(单位:)
16.下图是长方体和正方体的展开图,根据图上数据,求出表面积和体积。
参考答案:
1.236平方厘米
【分析】根据长方体的表面积公式:s=(ab+ah+bh)×2,代入数据计算即可。
【详解】(8×5+8×6+5×6)×2
=(40+48+30)×2
=118×2
=236(平方厘米)
答:表面积是236平方厘米。
【点睛】此题主要考查长方体的表面积的计算,牢记公式是关键。
2.216立方厘米;216平方厘米
【分析】正方体的体积=棱长×棱长×棱长,正方体的表面积=棱长×棱长×6。根据公式代入数据计算即可。
【详解】体积:6×6×6=216(立方厘米)
表面积:6×6×6=216(平方厘米)
【点睛】牢记公式,细心计算,注意单位。
3.13.12立方分米
【分析】观察组合体可知,是由一个长方体减去一个小长方体而成,根据长方体体积公式:长×宽×高即可解答。
【详解】5×0.8×4-[2×(5-1.6-1.6)×0.8]
=16-(2×1.8×0.8)
=16-2.88
=13.12(立方分米)
【点睛】此题主要考查学生的组合图形应用解题方法,需要掌握长方体的体积公式。
4.660立方分米
【分析】观察组合体可知,是由两个长方体拼接而成,根据长方体体积公式:长×宽×高即可解答。
【详解】5×5×12+(8-5)×10×12
=300+360
=660(立方分米)
【点睛】此题主要考查学生对组合图形的应用解题方法,需要掌握长方体的体积公式。
5.13392立方厘米
【分析】根据长方体的体积公式:长×宽×高,即可代数解答。
【详解】(50-16)×14×12+16×12×40
=34×14×12+16×12×40
=5712+7680
=13392(立方厘米)
【点睛】此题主要考查学生的长方体应用解题方法,需要掌握长方体的体积公式:长×宽×高。
6.(1)216立方厘米;(2)576立方厘米
【分析】(1)通过观察图形可知,图1的三条棱长分别等于3个小正方体棱长和,故正方体的棱长为:2×3,然后通过正方体体积公式:棱长×棱长×棱长即可解答;
(2)通过观察图形可知,图2的长=6个小正方体棱长和,故长为:2×6;宽=3个小正方体棱长和,故宽为:2×3;高=4个小正方体棱长和,故高为:2×4;然后通过长方体体积公式:长×宽×高即可解答。
【详解】(1)根据分析可知:棱长为:2×3=6(厘米)
6×6×6
=36×6
=216(立方厘米)
(2)根据分析可知:长:2×6=12(厘米),宽:2×3=6(厘米),高:2×4=8(厘米)
12×6×8
=72×8
=576(立方厘米)
【点睛】此题主要考查学生对正方体和长方体体积公式的理解与解答,同时,也考查了学生的空间想象力。
7.(1)207立方厘米;(2)231立方厘米
【分析】根据长方体体积公式:长×宽×高,分别求出两个长方体体积,然后再加在一起即可求出组合图形体积,即可解答。
【详解】(1)3×3×7+2×9×8
=63+144
=207(立方厘米)
(2)3×(5-2)×11+2×6×11
=99+132
=231(立方厘米)
【点睛】此题主要考查学生对组合图形体积的理解与分析解题能力,需要牢记长方体体积公式,即长×宽×高。
8.160平方米
【分析】将小正方体的上面下移至长方体与正方体接触面,所求面积可以看成一个长方体的表面积和正方体四个面的面积之和。长方体表面积公式:(长×宽+长×高+宽×高)×2;正方体表面积公式:棱长×棱长×6,根据基础公式灵活应用即可。
【详解】
(平方米)
答:立体图形的表面积是160平方米。
【点睛】此题主要考查正方体和长方体组合图形的表面积,需要理解所求面积可以看成一个长方体的表面积和正方体四个面的面积之和。
9.表面积960平方厘米;体积1600立方厘米。
【分析】由图可知此立方体是一个长宽高分别是15cm、15cm、8cm的一个大长方体去掉一个长宽高分别是5cm、5cm、8cm的小长方体的立体图形,立方体的表面积等于大长方体表面积-上下空缺的两个正方形面积+空缺内部左右两个长方形面积;立方体的体积=大长方体的体积-空缺部分小长方体的体积。
【详解】表面积:(15×15+15×8+15×8)×2-5×5×2+5×8×2
=930-50+80
=960(平方厘米)
体积:15×15×8-5×5×8
=1800-200
=1600(立方厘米)
答:立方体的表面积是960平方厘米;体积是1600立方厘米。
【点睛】此题考查组合体的表面积及体积的计算,注意认真观察图形求表面积时不要多加面也不要少减面。
10.(1)324cm2;360cm3
(2)30m2;6m3
【分析】(1)根据长方体表面积公式S=(ab+ah+bh)×2,体积公式V=abh,代入数据计算求解。
(2)组合图形的表面积=正方体表面积-长方体上下面的面积+长方体的侧面积,其中长方体上下面是2个边长为1m的正方形,长方体的侧面是4个相同的长为2m、宽为1m的长方形;根据正方体的表面积公式S=6a2,正方形的面积公式S=a2,长方形的面积公式S=ab;代入数据计算求解;
组合图形的体积=正方体的体积-长方体的体积;根据正方体的体积公式V=a3,长方体的体积公式V=abh,代入数据计算求解。
【详解】(1)表面积:
(12×6+12×5+6×5)×2
=(72+60+30)×2
=162×2
=324(cm2)
体积:
12×6×5=360(cm3)
长方体的表面积是324cm2,体积是360cm3。
(2)表面积:
2×2×6-1×1×2+2×1×4
=24-2+8
=30(m2)
体积:
2×2×2-1×1×2
=8-2
=6(m3)
组合图形的表面积是30m2,体积是6m3。
11.(1)1350平方厘米;3375立方厘米
(2)508平方厘米;700立方厘米
【分析】(1)正方体的表面积=棱长×棱长×6;正方体的体积=棱长×棱长×棱长;
(2)根据题图可将几何体看成一个长为12厘米、宽为7厘米、高为10厘米的长方体,再减去长为5厘米、宽为(12-8)厘米的两个长方形即可;用这个长方体的体积减去长为7厘米、高为5厘米、宽为(12-8)厘米的长方体体积即可。
【详解】(1)15×15×6
=225×6
=1350(平方厘米);
15×15×15
=225×15
=3375(立方厘米);
(2)(12×7+12×10+7×10)×2-(12-8)×5×2
=274×2-40
=508(平方厘米);
(2)12×7×10-7×5×(12-8)
=840-140
=700(立方厘米)
12.120cm3
【分析】水面上升的体积就是铁块的体积,长方体容器的长×宽×上升的水的高度=铁块体积,据此列式计算。
【详解】10×8×(9.5-8)
=80×1.5
=120(cm3)
13.126平方厘米
【详解】略
14.512立方厘米
【详解】12×(4+4)×4+(20-12)×4×4
=12×8×4+128
=384+128
=512(立方厘米),
答:这个组合图形的体积是512立方厘米
15.88平方厘米;48立方厘米
【分析】由题图可知:长方体两个长与两个宽的和是16厘米,据此求出长方体的长,再根据表面积和体积公式解答即可。
【详解】
=8-2
=6(厘米);
=44×2
=88(平方厘米);
体积:
=24×4
=96(立方厘米);
答:长方体纸盒的表面积是88平方厘米,体积是96立方厘米。
【点睛】本题考查根据展开图还原长方体的知识,它的关键是先确定长方体的长、宽、高,再求出长方体的表面积和体积。
16.长方体的表面积:10平方厘米;长方体的体积: 2立方厘米;
正方体的表面积:54平方分米;正方体的体积:27立方分米
【分析】由图意可知:长方体的长、宽、高分别为2厘米、1厘米和1厘米,正方体的棱长是3分米,分别利用长方体的表面积公式S=(ab+bh+ah)×2和长方体的体积公式V=abh,正方体的表面积公式S=6a2和正方体的体积公式V=a3即可求出其表面积和体积。
【详解】长方体的表面积:
(2×1+2×1+1×1)×2
=(2+2+1)×2
=5×2
=10(平方厘米);
长方体的体积:2×1×1=2(立方厘米)
正方体的表面积:
3×3×6
=9×6
=54(平方分米);
正方体的体积:
3×3×3
=9×3
=27(立方分米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
