2023-2024学年浙江省温州市龙湾区部分学校九年级(上)返校考数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年浙江省温州市龙湾区部分学校九年级(上)返校考数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 409.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 15:39:08 | ||
图片预览


文档简介
2023-2024学年浙江省温州市龙湾区部分学校九年级(上)返校考数学试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1.数,,,中最小的是( )
A. B. C. D.
2.下列电视台图标,属于中心对称图形的是( )
A. B. C. D.
3.根据教育部门统计,年全国普通高校毕业生规模预计将会达到惊人的人,其中数据用科学记数法表示为( )
A. B. C. D.
4.如图是某校九年级学生最喜欢球类运动的人数统计图若选择排球的有人,则选择篮球的有( )
A. 人
B. 人
C. 人
D. 人
5.化简的结果是( )
A. B. C. D.
6.当,时,代数式的值为( )
A. B. C. D.
7.如图,在平面直角坐标系中,点,,的坐标分别为,,将点向右平移个单位后得到点若点落在内包括边界,则的取值范围是( )
A.
B.
C.
D.
8.某地水稻种植基地在,两个面积相同的试验田里种植不同品种的水稻,分别收获吨和吨,已知试验田的水稻比试验田的水稻每公顷少收吨设试验田每公顷产量为吨,则可以列出方程为( )
A. B. C. D.
9.图是第届国际数学奥林匹克竞赛会标,图是其主体的中间部分图案,它是一个轴对称图形已知,,作菱形,使点,,分别在,,上,且点在上若,则整个图形的面积为( )
A. B. C. D.
10.如图,点为矩形边上的一个动点,点从出发沿着矩形的四条边运动设点运动的路程长为,的面积为,图是随变化的函数图象,则矩形的对角线的长是( )
A. B. C. D.
二、填空题(本大题共6小题,共24.0分)
11.分解因式:______.
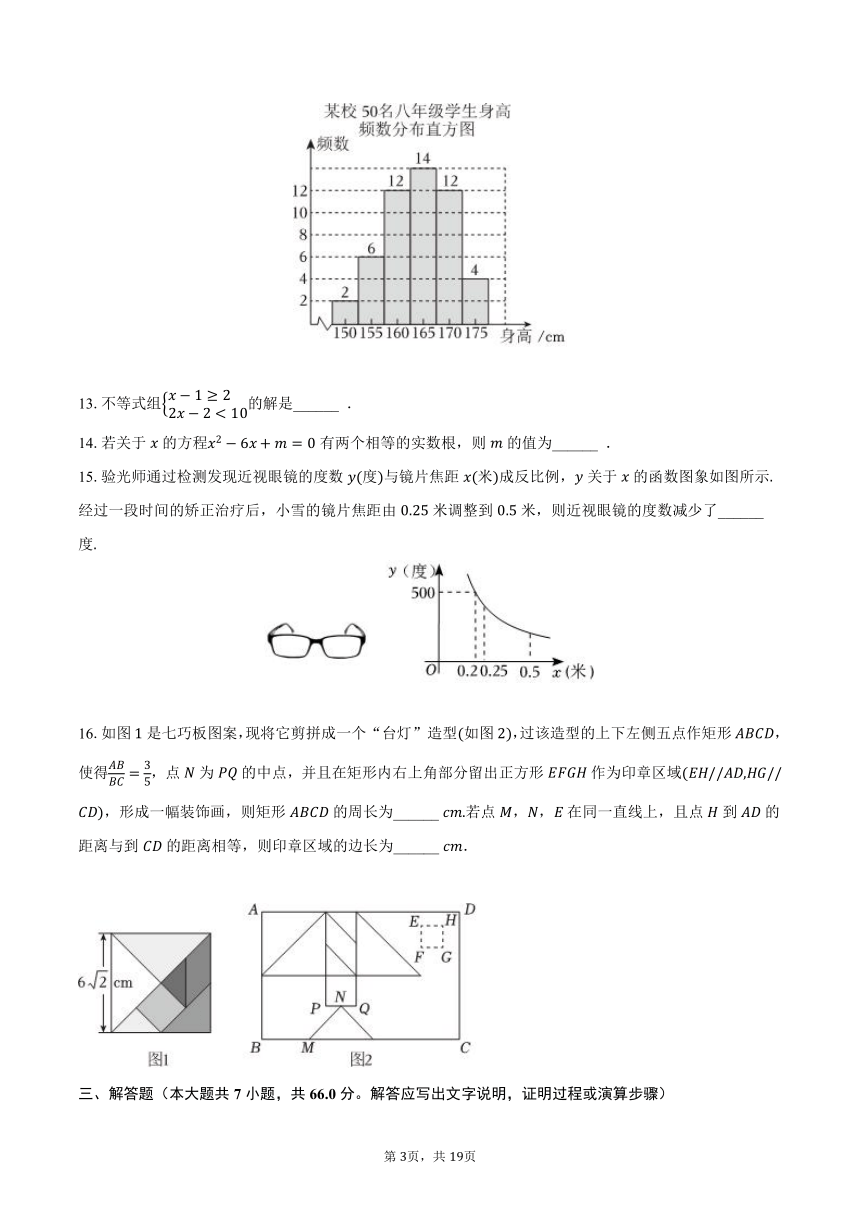
12.某校对名八年级学生身高进行统计,得到频数分布直方图每一组含前一个边界值,不含后一个边界值如图所示,其中身高在及以上的学生有______ 人
13.不等式组的解是______ .
14.若关于的方程有两个相等的实数根,则的值为______ .
15.验光师通过检测发现近视眼镜的度数度与镜片焦距米成反比例,关于的函数图象如图所示经过一段时间的矫正治疗后,小雪的镜片焦距由米调整到米,则近视眼镜的度数减少了______ 度
16.如图是七巧板图案,现将它剪拼成一个“台灯”造型如图,过该造型的上下左侧五点作矩形,使得,点为的中点,并且在矩形内右上角部分留出正方形作为印章区域,形成一幅装饰画,则矩形的周长为______ 若点,,在同一直线上,且点到的距离与到的距离相等,则印章区域的边长为______ .
三、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
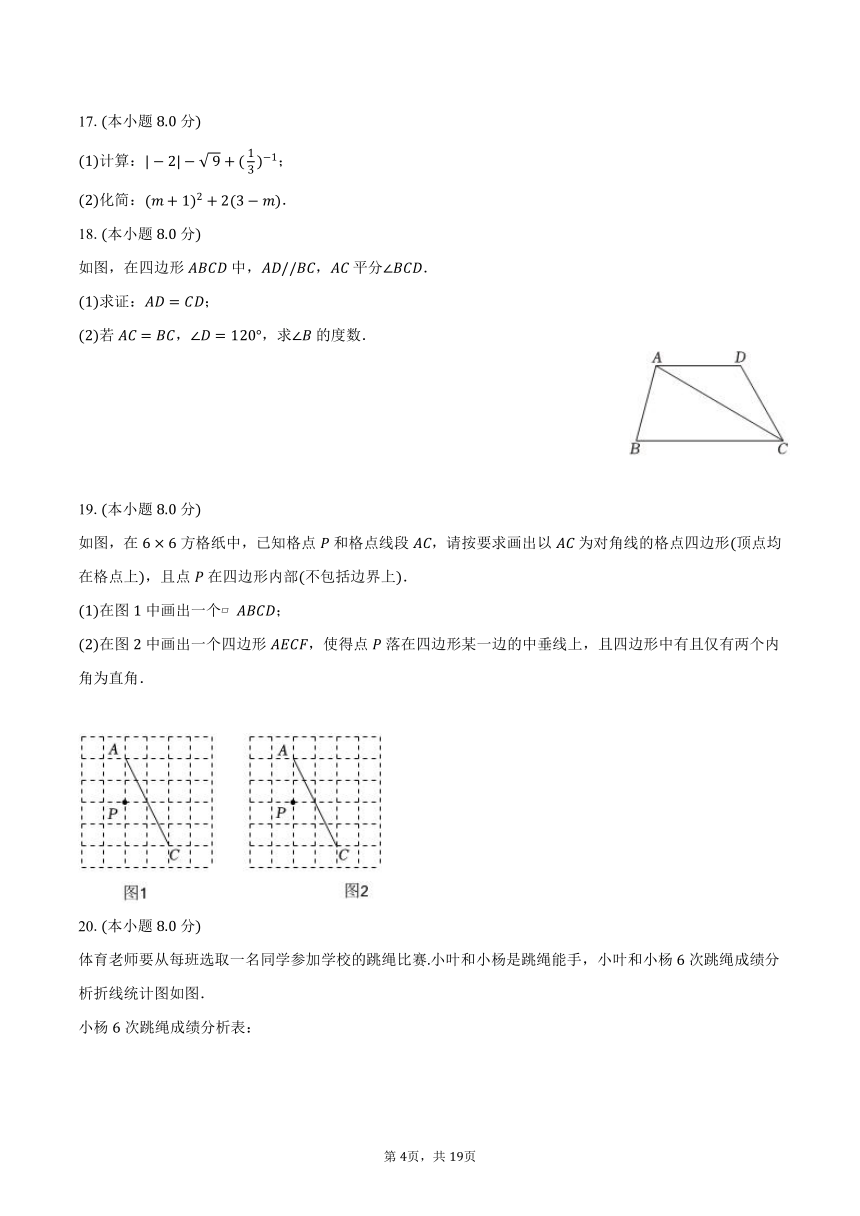
17.本小题分
计算:;
化简:.
18.本小题分
如图,在四边形中,,平分.
求证:;
若,,求的度数.
19.本小题分
如图,在方格纸中,已知格点和格点线段,请按要求画出以为对角线的格点四边形顶点均在格点上,且点在四边形内部不包括边界上.
在图中画出一个 ;
在图中画出一个四边形,使得点落在四边形某一边的中垂线上,且四边形中有且仅有两个内角为直角.
20.本小题分
体育老师要从每班选取一名同学参加学校的跳绳比赛小叶和小杨是跳绳能手,小叶和小杨次跳绳成绩分析折线统计图如图.
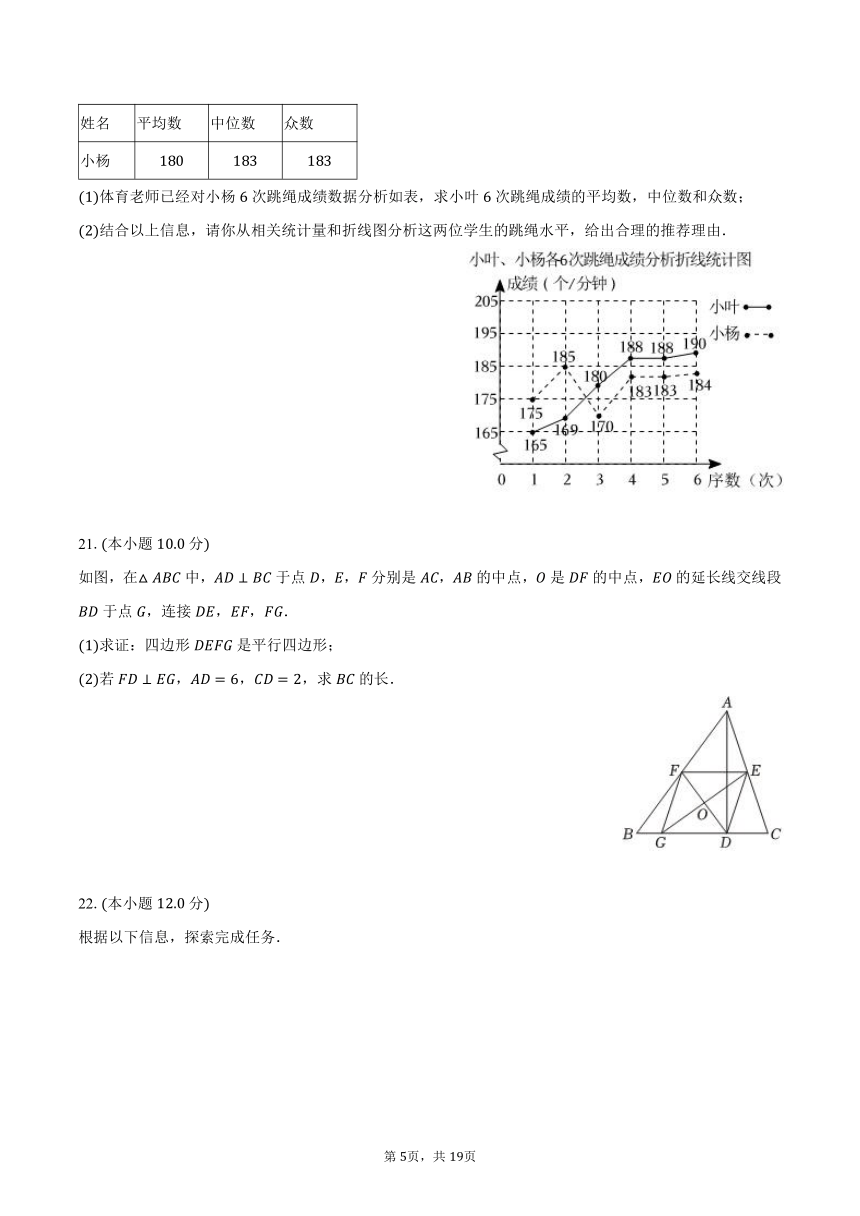
小杨次跳绳成绩分析表:
姓名 平均数 中位数 众数
小杨
体育老师已经对小杨次跳绳成绩数据分析如表,求小叶次跳绳成绩的平均数,中位数和众数;
结合以上信息,请你从相关统计量和折线图分析这两位学生的跳绳水平,给出合理的推荐理由.
21.本小题分
如图,在中,于点,,分别是,的中点,是的中点,的延长线交线段于点,连接,,.
求证:四边形是平行四边形;
若,,,求的长.
22.本小题分
根据以下信息,探索完成任务.
如何设计种植方案?
素材 某校为响应国家政策,在校内平方米的土地上进行种植课实践,现有、,三种作物的相关信息如表所示已知株作物和株作物的产量共为千克:株作物和株作物的产量共为千克. 作物作物作物每平方米种植株树株单株产量千克
素材 由于作物植株间距较大,可增加作物每平方米的种植株树经过实验发现,每平方米种植作物每增加株,作物的单株产量减少千克而,单株产量不发生变化.
素材 若同时种植,,三种作物,实行分区域种植.
问题解决
任务 确定单株产量 求,的值.
单一种植全部种植作物 任务 预估种植策略 要使作物每平方米产量为千克,则每平方米应种植多少株?
分区种植种植,,三种作物 任务 规划种植方案 设这平方米的土地中有平方米用于种植作物,且每平方米的产量最大:有平方米用于种植作物,剩余的全用来种植作物,,均为正整数当这平方米总产量为千克时,求这三种作物的种植方案.
23.本小题分
如图,已知,在中,,,,点,分别从点,出发沿线段,向终点,匀速移动,,两点同时出发,同时到达终点设,.
求和的长;
求关于的函数表达式;
如图,过点作于点,连接,.
当为直角三角形时,求的值;
作点关于的对称点,当点落在的延长线上时,求的值.
答案和解析
1.【答案】
【解析】解:由题意知,,
故选:.
根据负数小于正数和得出结论即可.
本题主要考查实数大小的比较,熟练掌握实数大小比较的方法是解题的关键.
2.【答案】
【解析】解:选项A、、中的图形都不能找到一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形.
选项B中的图形能找到一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形.
故选:.
根据中心对称图形的概念判断.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
本题考查的是中心对称图形,中心对称图形是要寻找对称中心,旋转度后与自身重合.
3.【答案】
【解析】解:,
故选:.
将一个数表示成的形式,其中,为整数,这种记数方法叫做科学记数法,据此即可得出答案.
本题考查科学记数法表示较大的数,熟练掌握其定义是解题的关键.
4.【答案】
【解析】解:人,人,
故选:.
根据统计图求出总人数,然后按比例求出选择篮球的人数即可.
本题主要考查扇形统计图的知识,熟练掌握扇形统计图的知识是解题的关键.
5.【答案】
【解析】解:原式.
故选:.
根据互为相反数的偶次幂相等,可化成同底数幂的乘法,根据同底数幂的乘法,底数不变指数相加,可得答案.
本题考查了同底数幂的乘法,先化成同底数幂的乘法,再进行同底数幂的乘法运算.
6.【答案】
【解析】解:
,
当,时,
原式
,
故选:.
先根据去括号法则把所求代数式进行化简,然后把,代入化简的结果,进行计算即可.
本题主要考查了整式的化简求值,解题关键是熟练掌握去括号法则和合并同类项法则.
7.【答案】
【解析】解:,的坐标分别为,,
中点和中点的坐标分别为,,
的坐标为,,,
的取值范围是.
故选:.
先求出中点和中点的坐标,依此即可求出的取值范围.
本题考查了坐标与图形变化平移,关键是求出中点和中点的坐标.
8.【答案】
【解析】解:根据题意,得,
故选:.
根据,两个实验田的面积相等列分式方程即可.
本题考查了由实际问题抽象出分式方程,理解题意并根据题意建立等量关系是解题的关键.
9.【答案】
【解析】解:由题意,整个图形是轴对称图形,
,,≌.
又,
.
是等边三角形.
.
,,
.
从而,和为边长是的全等的等边三角形,菱形的面积是是等边三角形面积的倍.
边长为的等边三角形的面积为,
是等边三角形的面积,
菱形的面积,
的面积和的面积均为.
整个图形的面积.
故选:.
依据题意,根据对称性,,又,进而可以判断,故可是等边三角形,菱形的面积是是等边三角形面积的倍,又由题意,和为全等的等边三角形,从而可以得解.
本题主要考查了菱形的性质、轴对称图形的性质,解题时要熟练掌握并理解是关键.
10.【答案】
【解析】解:由图可知,
点运动一周的路程是,
即.
所以.
又的面积的最大值为,
即点在上运动时,
所以,
则.
所以,
则,
所以.
在中,
,
则.
故选:.
由图和图可知长方形的周长及面积,再结合整体思想即可解决问题.
本题考查动点运动的函数图象,能将图和图联系起来,并得出关于矩形长和宽的方程是解决问题的关键.
11.【答案】
【解析】解:.
直接提取公因式即可.
本题考查因式分解,因式分解的步骤为:一提公因式;二看公式.一般来说,如果可以提取公因式的要先提取公因式,再看剩下的因式是否还能分解.
12.【答案】
【解析】解:人,
故答案为:.
将身高在及以上的三组频数相加即可得到答案.
本题考查频数分布直方图,能从统计图中获取有用信息是解题的关键.
13.【答案】
【解析】解:解不等式,得:,
解不等式得:,
则不等式组的解集为,
故答案为:.
分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
14.【答案】
【解析】解:关于的方程有两个相等的实数根,
,即,
解得,
故答案为:.
关于的方程有两个相等的实数根,则,据此列出关于的新方程,通过解新方程即可求得的值.
本题考查了根的判别式.一元二次方程根的情况与判别式的关系:
方程有两个不相等的实数根;
方程有两个相等的实数根;
方程没有实数根.
15.【答案】
【解析】解:设,
在图象上,
,
函数解析式为:,
当时,,
当时,,
度数减少了度,
故答案为:.
由已知设,则有图象知点满足解析式,代入求,则解析式为:,令,时,分别求的值后作差即可.
本题考查待定系数法求反比例函数解析式,以及反比例函数的实际应用,读懂题意,掌握课本知识是解决问题的关键.
16.【答案】
【解析】解:由图可知,
七巧板中的等腰直角三角形最大的直角边长为,然后,最小的直角边长为,
正方形和平行四边形的短边长都是.
过点作和的垂线,垂足分别为,,
则,
又,且是等腰直角三角形,
所以,
故JK.
又,
所以四边形是矩形,
所以.
又,
所以,
故矩形的周长为.
延长经过点与交于点,连接,
因为,且,
所以.
又点到和的距离相等,
所以点在的角平分线上,
则.
所以,
所以,
又,
所以四边形是平行四边形.
又,,
所以.
所以.
则.
故答案为:,.
根据“台灯”的造型及图,可求出的长,进而可求出矩形的周长;延长经过点并与相交于点,连接,可得出四边形是平行四边形,求出长即可解决问题.
本题考查正方形的性质及矩形的性质,能由图求出各图形的边长是解题的关键.
17.【答案】解:原式
;
原式
.
【解析】利用绝对值的性质,算术平方根的定义及负整数指数幂进行计算即可;
利用完全平方公式进行计算即可.
本题考查实数及整式的运算,熟练掌握相关运算法则是解题的关键.
18.【答案】证明:平分,
,
,
,
,
;
解:,
,
,
,
.
【解析】根据角平分线的定义和平行线的性质证得,由等腰三角形的判定可得;
根据等腰三角形的性质结合三角形内角和定理即可求得答案.
本题主要考查了等腰三角形的性质和判定,三角形内角和定理,平行线的性质,熟练掌握相关性质定理是解决问题的关键.
19.【答案】解:如图: 即为所求;
如图:四边形即为所求.
【解析】根据平行四边形的判定定理作图;
根据线段的垂直平分线的性质作图.
本题考查了复杂作图,掌握特殊四边形的判定定理是解题的关键.
20.【答案】解:小叶次跳绳成绩的平均数为:个分钟,
中位数为个分钟,
众数为个分钟;
从平均数来看,小叶的平均数与小杨一样,均为个分钟,
从中位数来看,小杨的中位数为个分钟,小叶的中位数为个分钟,所以选择推荐小叶参加比赛;
从众数来看,小杨的众数为个分钟,小叶的众数为个分钟,所以选择推荐小叶参加比赛;
从折线图来看,小叶是稳步提升的,所以推荐小叶参加学校比赛.
【解析】根据加权平均数,中位数和众数的定义解答即可;
结合的结论解答即可.
本题考查了折线统计图,加权平均数,中位数和众数,利用加权平均数的公式,众数的定义,中位数的定义是解题关键.
21.【答案】证明:,分别是,的中点,
是的中位线,
,
,
是的中点,
,
在和中,
,
≌,
,
四边形是平行四边形.
解:
,
,,
,
是的中点,
,
,
是菱形,
,
.
【解析】由三角形中位线定理得,则,再证≌,得,然后由平行四边形的判定即可得出结论;
根据勾股定理得出,进而理由菱形的判定和性质解答即可.
本题是四边形综合题,考查了平行四边形的判定与性质、全等三角形的判定与性质、菱形的判定和性质、勾股定理等知识,熟练掌握平行四边形的判定与性质是解题的关键.
22.【答案】解:任务:由题意可得:
解得:
答:,的值分别为,;
任务:每平方米种植作物每增加株,
由题意可得:,
解得:,,
,,
每平方米应种植株或株;
任务:,
作物每平方米的最大产量为千克,
由题意可得:,
.,
,均为正整数,
,,,,
共有两种方案:第一种,种植作物平方米,种植作物平方米,种植作物平方米;
第二种:种植作物平方米,种植作物平方米,种植作物平方米.
【解析】根据题意,列出方程组解答即可;
根据题意列出,解答即可;
根据题意列出关于、的关系式,依据、取正整数,推出种植方案即可.
本题考查了二次函数的实际应用,读懂题意列出关系式是解答本题的关键.
23.【答案】解:,,,
,
,
由题意可设,
当时,,当时,;
,解得,
关于的函数表达式为;
,
,
,
,
为直角三角形,可分为两种情况.
当时,如图,
,
,
,
,
,
即,
;
当时,如图,
,,
,
,
四边形为平行四边形,
,
,
,
,
,
;
综上所述,为或;
当点落在的延长线上时,如图,
,
,
又由对称可知:,
,
为等边三角形,
同理可得为等边三角形,
,
又,
,
.
【解析】由直角三角形的性质及勾股定理可得出答案;
由待定系数法可求出答案;
分两种情况,由直角三角形的性质可得出答案;
证出为等边三角形,同理可得为等边三角形,由等边三角形的性质可得出答案.
本题是三角形综合题,考查了勾股定理,直角三角形的判定与性质,待定系数法,等边三角形的判定与性质,平行四边形的判定与性质,正确进行分类是解题的关键.
第1页,共1页
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1.数,,,中最小的是( )
A. B. C. D.
2.下列电视台图标,属于中心对称图形的是( )
A. B. C. D.
3.根据教育部门统计,年全国普通高校毕业生规模预计将会达到惊人的人,其中数据用科学记数法表示为( )
A. B. C. D.
4.如图是某校九年级学生最喜欢球类运动的人数统计图若选择排球的有人,则选择篮球的有( )
A. 人
B. 人
C. 人
D. 人
5.化简的结果是( )
A. B. C. D.
6.当,时,代数式的值为( )
A. B. C. D.
7.如图,在平面直角坐标系中,点,,的坐标分别为,,将点向右平移个单位后得到点若点落在内包括边界,则的取值范围是( )
A.
B.
C.
D.
8.某地水稻种植基地在,两个面积相同的试验田里种植不同品种的水稻,分别收获吨和吨,已知试验田的水稻比试验田的水稻每公顷少收吨设试验田每公顷产量为吨,则可以列出方程为( )
A. B. C. D.
9.图是第届国际数学奥林匹克竞赛会标,图是其主体的中间部分图案,它是一个轴对称图形已知,,作菱形,使点,,分别在,,上,且点在上若,则整个图形的面积为( )
A. B. C. D.
10.如图,点为矩形边上的一个动点,点从出发沿着矩形的四条边运动设点运动的路程长为,的面积为,图是随变化的函数图象,则矩形的对角线的长是( )
A. B. C. D.
二、填空题(本大题共6小题,共24.0分)
11.分解因式:______.
12.某校对名八年级学生身高进行统计,得到频数分布直方图每一组含前一个边界值,不含后一个边界值如图所示,其中身高在及以上的学生有______ 人
13.不等式组的解是______ .
14.若关于的方程有两个相等的实数根,则的值为______ .
15.验光师通过检测发现近视眼镜的度数度与镜片焦距米成反比例,关于的函数图象如图所示经过一段时间的矫正治疗后,小雪的镜片焦距由米调整到米,则近视眼镜的度数减少了______ 度
16.如图是七巧板图案,现将它剪拼成一个“台灯”造型如图,过该造型的上下左侧五点作矩形,使得,点为的中点,并且在矩形内右上角部分留出正方形作为印章区域,形成一幅装饰画,则矩形的周长为______ 若点,,在同一直线上,且点到的距离与到的距离相等,则印章区域的边长为______ .
三、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
计算:;
化简:.
18.本小题分
如图,在四边形中,,平分.
求证:;
若,,求的度数.
19.本小题分
如图,在方格纸中,已知格点和格点线段,请按要求画出以为对角线的格点四边形顶点均在格点上,且点在四边形内部不包括边界上.
在图中画出一个 ;
在图中画出一个四边形,使得点落在四边形某一边的中垂线上,且四边形中有且仅有两个内角为直角.
20.本小题分
体育老师要从每班选取一名同学参加学校的跳绳比赛小叶和小杨是跳绳能手,小叶和小杨次跳绳成绩分析折线统计图如图.
小杨次跳绳成绩分析表:
姓名 平均数 中位数 众数
小杨
体育老师已经对小杨次跳绳成绩数据分析如表,求小叶次跳绳成绩的平均数,中位数和众数;
结合以上信息,请你从相关统计量和折线图分析这两位学生的跳绳水平,给出合理的推荐理由.
21.本小题分
如图,在中,于点,,分别是,的中点,是的中点,的延长线交线段于点,连接,,.
求证:四边形是平行四边形;
若,,,求的长.
22.本小题分
根据以下信息,探索完成任务.
如何设计种植方案?
素材 某校为响应国家政策,在校内平方米的土地上进行种植课实践,现有、,三种作物的相关信息如表所示已知株作物和株作物的产量共为千克:株作物和株作物的产量共为千克. 作物作物作物每平方米种植株树株单株产量千克
素材 由于作物植株间距较大,可增加作物每平方米的种植株树经过实验发现,每平方米种植作物每增加株,作物的单株产量减少千克而,单株产量不发生变化.
素材 若同时种植,,三种作物,实行分区域种植.
问题解决
任务 确定单株产量 求,的值.
单一种植全部种植作物 任务 预估种植策略 要使作物每平方米产量为千克,则每平方米应种植多少株?
分区种植种植,,三种作物 任务 规划种植方案 设这平方米的土地中有平方米用于种植作物,且每平方米的产量最大:有平方米用于种植作物,剩余的全用来种植作物,,均为正整数当这平方米总产量为千克时,求这三种作物的种植方案.
23.本小题分
如图,已知,在中,,,,点,分别从点,出发沿线段,向终点,匀速移动,,两点同时出发,同时到达终点设,.
求和的长;
求关于的函数表达式;
如图,过点作于点,连接,.
当为直角三角形时,求的值;
作点关于的对称点,当点落在的延长线上时,求的值.
答案和解析
1.【答案】
【解析】解:由题意知,,
故选:.
根据负数小于正数和得出结论即可.
本题主要考查实数大小的比较,熟练掌握实数大小比较的方法是解题的关键.
2.【答案】
【解析】解:选项A、、中的图形都不能找到一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形.
选项B中的图形能找到一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形.
故选:.
根据中心对称图形的概念判断.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
本题考查的是中心对称图形,中心对称图形是要寻找对称中心,旋转度后与自身重合.
3.【答案】
【解析】解:,
故选:.
将一个数表示成的形式,其中,为整数,这种记数方法叫做科学记数法,据此即可得出答案.
本题考查科学记数法表示较大的数,熟练掌握其定义是解题的关键.
4.【答案】
【解析】解:人,人,
故选:.
根据统计图求出总人数,然后按比例求出选择篮球的人数即可.
本题主要考查扇形统计图的知识,熟练掌握扇形统计图的知识是解题的关键.
5.【答案】
【解析】解:原式.
故选:.
根据互为相反数的偶次幂相等,可化成同底数幂的乘法,根据同底数幂的乘法,底数不变指数相加,可得答案.
本题考查了同底数幂的乘法,先化成同底数幂的乘法,再进行同底数幂的乘法运算.
6.【答案】
【解析】解:
,
当,时,
原式
,
故选:.
先根据去括号法则把所求代数式进行化简,然后把,代入化简的结果,进行计算即可.
本题主要考查了整式的化简求值,解题关键是熟练掌握去括号法则和合并同类项法则.
7.【答案】
【解析】解:,的坐标分别为,,
中点和中点的坐标分别为,,
的坐标为,,,
的取值范围是.
故选:.
先求出中点和中点的坐标,依此即可求出的取值范围.
本题考查了坐标与图形变化平移,关键是求出中点和中点的坐标.
8.【答案】
【解析】解:根据题意,得,
故选:.
根据,两个实验田的面积相等列分式方程即可.
本题考查了由实际问题抽象出分式方程,理解题意并根据题意建立等量关系是解题的关键.
9.【答案】
【解析】解:由题意,整个图形是轴对称图形,
,,≌.
又,
.
是等边三角形.
.
,,
.
从而,和为边长是的全等的等边三角形,菱形的面积是是等边三角形面积的倍.
边长为的等边三角形的面积为,
是等边三角形的面积,
菱形的面积,
的面积和的面积均为.
整个图形的面积.
故选:.
依据题意,根据对称性,,又,进而可以判断,故可是等边三角形,菱形的面积是是等边三角形面积的倍,又由题意,和为全等的等边三角形,从而可以得解.
本题主要考查了菱形的性质、轴对称图形的性质,解题时要熟练掌握并理解是关键.
10.【答案】
【解析】解:由图可知,
点运动一周的路程是,
即.
所以.
又的面积的最大值为,
即点在上运动时,
所以,
则.
所以,
则,
所以.
在中,
,
则.
故选:.
由图和图可知长方形的周长及面积,再结合整体思想即可解决问题.
本题考查动点运动的函数图象,能将图和图联系起来,并得出关于矩形长和宽的方程是解决问题的关键.
11.【答案】
【解析】解:.
直接提取公因式即可.
本题考查因式分解,因式分解的步骤为:一提公因式;二看公式.一般来说,如果可以提取公因式的要先提取公因式,再看剩下的因式是否还能分解.
12.【答案】
【解析】解:人,
故答案为:.
将身高在及以上的三组频数相加即可得到答案.
本题考查频数分布直方图,能从统计图中获取有用信息是解题的关键.
13.【答案】
【解析】解:解不等式,得:,
解不等式得:,
则不等式组的解集为,
故答案为:.
分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
14.【答案】
【解析】解:关于的方程有两个相等的实数根,
,即,
解得,
故答案为:.
关于的方程有两个相等的实数根,则,据此列出关于的新方程,通过解新方程即可求得的值.
本题考查了根的判别式.一元二次方程根的情况与判别式的关系:
方程有两个不相等的实数根;
方程有两个相等的实数根;
方程没有实数根.
15.【答案】
【解析】解:设,
在图象上,
,
函数解析式为:,
当时,,
当时,,
度数减少了度,
故答案为:.
由已知设,则有图象知点满足解析式,代入求,则解析式为:,令,时,分别求的值后作差即可.
本题考查待定系数法求反比例函数解析式,以及反比例函数的实际应用,读懂题意,掌握课本知识是解决问题的关键.
16.【答案】
【解析】解:由图可知,
七巧板中的等腰直角三角形最大的直角边长为,然后,最小的直角边长为,
正方形和平行四边形的短边长都是.
过点作和的垂线,垂足分别为,,
则,
又,且是等腰直角三角形,
所以,
故JK.
又,
所以四边形是矩形,
所以.
又,
所以,
故矩形的周长为.
延长经过点与交于点,连接,
因为,且,
所以.
又点到和的距离相等,
所以点在的角平分线上,
则.
所以,
所以,
又,
所以四边形是平行四边形.
又,,
所以.
所以.
则.
故答案为:,.
根据“台灯”的造型及图,可求出的长,进而可求出矩形的周长;延长经过点并与相交于点,连接,可得出四边形是平行四边形,求出长即可解决问题.
本题考查正方形的性质及矩形的性质,能由图求出各图形的边长是解题的关键.
17.【答案】解:原式
;
原式
.
【解析】利用绝对值的性质,算术平方根的定义及负整数指数幂进行计算即可;
利用完全平方公式进行计算即可.
本题考查实数及整式的运算,熟练掌握相关运算法则是解题的关键.
18.【答案】证明:平分,
,
,
,
,
;
解:,
,
,
,
.
【解析】根据角平分线的定义和平行线的性质证得,由等腰三角形的判定可得;
根据等腰三角形的性质结合三角形内角和定理即可求得答案.
本题主要考查了等腰三角形的性质和判定,三角形内角和定理,平行线的性质,熟练掌握相关性质定理是解决问题的关键.
19.【答案】解:如图: 即为所求;
如图:四边形即为所求.
【解析】根据平行四边形的判定定理作图;
根据线段的垂直平分线的性质作图.
本题考查了复杂作图,掌握特殊四边形的判定定理是解题的关键.
20.【答案】解:小叶次跳绳成绩的平均数为:个分钟,
中位数为个分钟,
众数为个分钟;
从平均数来看,小叶的平均数与小杨一样,均为个分钟,
从中位数来看,小杨的中位数为个分钟,小叶的中位数为个分钟,所以选择推荐小叶参加比赛;
从众数来看,小杨的众数为个分钟,小叶的众数为个分钟,所以选择推荐小叶参加比赛;
从折线图来看,小叶是稳步提升的,所以推荐小叶参加学校比赛.
【解析】根据加权平均数,中位数和众数的定义解答即可;
结合的结论解答即可.
本题考查了折线统计图,加权平均数,中位数和众数,利用加权平均数的公式,众数的定义,中位数的定义是解题关键.
21.【答案】证明:,分别是,的中点,
是的中位线,
,
,
是的中点,
,
在和中,
,
≌,
,
四边形是平行四边形.
解:
,
,,
,
是的中点,
,
,
是菱形,
,
.
【解析】由三角形中位线定理得,则,再证≌,得,然后由平行四边形的判定即可得出结论;
根据勾股定理得出,进而理由菱形的判定和性质解答即可.
本题是四边形综合题,考查了平行四边形的判定与性质、全等三角形的判定与性质、菱形的判定和性质、勾股定理等知识,熟练掌握平行四边形的判定与性质是解题的关键.
22.【答案】解:任务:由题意可得:
解得:
答:,的值分别为,;
任务:每平方米种植作物每增加株,
由题意可得:,
解得:,,
,,
每平方米应种植株或株;
任务:,
作物每平方米的最大产量为千克,
由题意可得:,
.,
,均为正整数,
,,,,
共有两种方案:第一种,种植作物平方米,种植作物平方米,种植作物平方米;
第二种:种植作物平方米,种植作物平方米,种植作物平方米.
【解析】根据题意,列出方程组解答即可;
根据题意列出,解答即可;
根据题意列出关于、的关系式,依据、取正整数,推出种植方案即可.
本题考查了二次函数的实际应用,读懂题意列出关系式是解答本题的关键.
23.【答案】解:,,,
,
,
由题意可设,
当时,,当时,;
,解得,
关于的函数表达式为;
,
,
,
,
为直角三角形,可分为两种情况.
当时,如图,
,
,
,
,
,
即,
;
当时,如图,
,,
,
,
四边形为平行四边形,
,
,
,
,
,
;
综上所述,为或;
当点落在的延长线上时,如图,
,
,
又由对称可知:,
,
为等边三角形,
同理可得为等边三角形,
,
又,
,
.
【解析】由直角三角形的性质及勾股定理可得出答案;
由待定系数法可求出答案;
分两种情况,由直角三角形的性质可得出答案;
证出为等边三角形,同理可得为等边三角形,由等边三角形的性质可得出答案.
本题是三角形综合题,考查了勾股定理,直角三角形的判定与性质,待定系数法,等边三角形的判定与性质,平行四边形的判定与性质,正确进行分类是解题的关键.
第1页,共1页
同课章节目录
