人教A版(2019)选择性必修第二册4.1数列的概念(第1课时)课件(共21张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第二册4.1数列的概念(第1课时)课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 13:35:13 | ||
图片预览




文档简介
(共21张PPT)
人教A版(2019)高中数学选择性必修二
4.1 数列的概念
第一课时
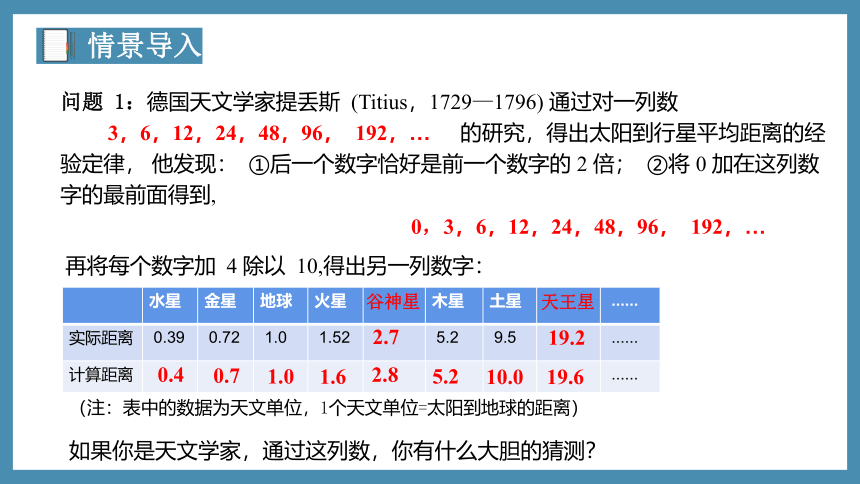
问题 1:德国天文学家提丢斯 (Titius,1729—1796) 通过对一列数
3,6,12,24,48,96, 192,… 的研究,得出太阳到行星平均距离的经验定律, 他发现: ①后一个数字恰好是前一个数字的 2 倍; ②将 0 加在这列数字的最前面得到,
水星 金星 地球 火星 木星 土星 ......
实际距离 0.39 0.72 1.0 1.52 5.2 9.5 ......
计算距离 ......
0,3,6,12,24,48,96, 192,…
0.4
0.7
1.0
1.6
2.8
5.2
10.0
19.6
(注:表中的数据为天文单位,1个天文单位=太阳到地球的距离)
2.7
19.2
谷神星
天王星
再将每个数字加 4 除以 10,得出另一列数字:
如果你是天文学家,通过这列数,你有什么大胆的猜测?
情景导入
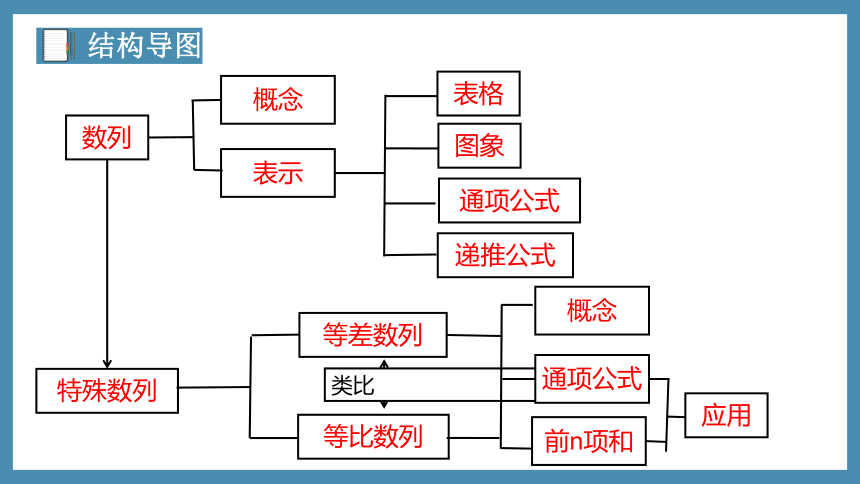
数列
概念
表示
表格
图象
通项公式
递推公式
特殊数列
等差数列
等比数列
类比
概念
前n项和
通项公式
应用
结构导图
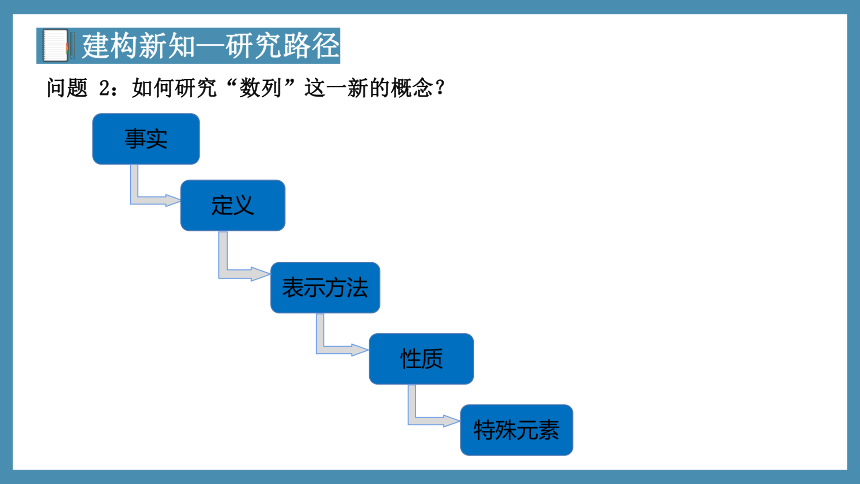
问题 2:如何研究“数列”这一新的概念?
事实
定义
表示方法
性质
特殊元素
建构新知—研究路径
(1):王芳从 1 岁到 17 岁每年的身高依次排成一列数:
75,87,96,103,110, 116,120,128,138,145,153,158,160,162,163,165,168. 它们之间能否交换位置?具有确定的顺序吗?
(2):在两河流域发掘的一块泥版上就有一列依次表示一个月中从第 1 天到第 15 天每天月亮可见部分的数:
5,10,20,40,80,96,112,128,144,160,176,192,208,224,240. 它们之间能否交换位置?具有确定的顺序吗?
的n次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数
这也是具有确定顺序的一列数吗?
建构新知—形成概念
一般地,我们把按照确定的顺序排列的一列数称为数列。
数列中的每一个数叫做这个数列的项。
一、数列的概念
追问1: 1,3,5,7 和 7,5,3,1 这两个数列是不是同一个数列?
追问2: 1,1,1,1 是一个数列吗?
问题 4:如何用一般的符号表示数列?
不是
是
建构新知—形成概念
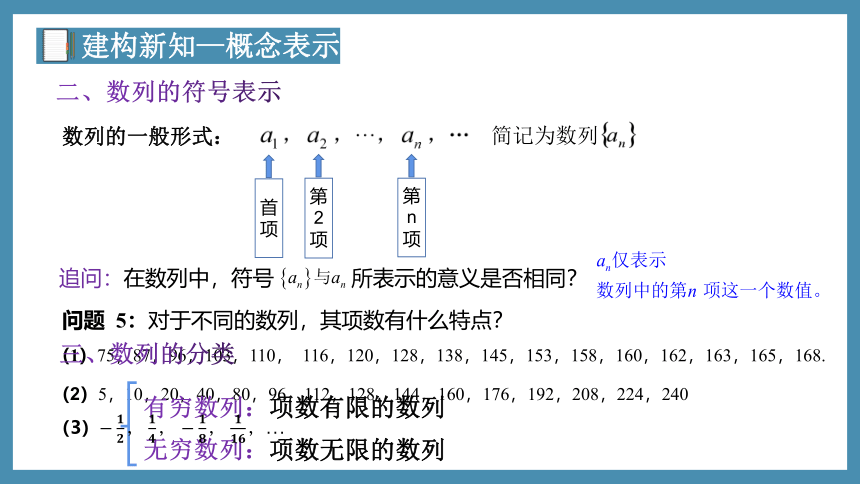
二、数列的符号表示
数列的一般形式:
简记为数列
首项
第2项
第n项
追问:在数列中,符号 所表示的意义是否相同?
问题 5:对于不同的数列,其项数有什么特点?
(1)75,87,96,103,110, 116,120,128,138,145,153,158,160,162,163,165,168.
(2)5,10,20,40,80,96,112,128,144,160,176,192,208,224,240
三、数列的分类
有穷数列:项数有限的数列
无穷数列:项数无限的数列
(3)
建构新知—概念表示
问题 6:数列 中的各项 与各项序号k(k=1,2,3,···,n,···)之间的对应关系是什么关系?
序号
项
函数关系
追问: 和 是同一个数列吗?你能否从函数的角度解释一下?
因为定义域不同,所以它们不是同一个数列。
建构新知—概念辨析
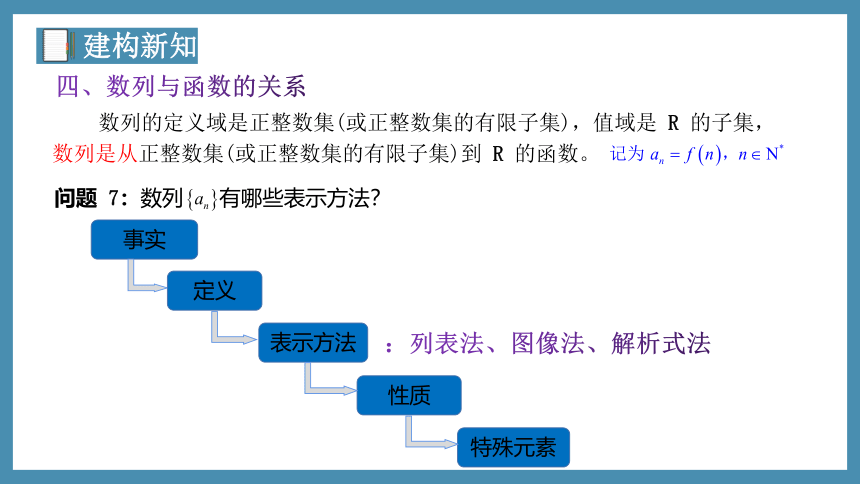
四、数列与函数的关系
数列的定义域是正整数集(或正整数集的有限子集),值域是 R 的子集,
数列是从正整数集(或正整数集的有限子集)到 R 的函数。
问题 7:数列 有哪些表示方法?
事实
定义
表示方法
性质
特殊元素
:列表法、图像法、解析式法
建构新知
问题 7:数列 有哪些表示方法?
列表法、图像法、解析式法
75,87,96,103,110,116,120,128,138,145,153,158,160,162,163,165,168.
建构新知
追问1 :数列的图像有什么特点?
75,87,96,103,110,116,120,128,138,145,153,158,160,162,163,165,168.
追问2:类比函数的解析式,数列有怎样的解析式呢?
数列的图像是由一系列离散的点构成的。
为什么?
建构新知
如果数列{an}的_________与它的________之间的对应关系可以用一个式子来表示,那么这个式子就是数列的函数解析式,叫做这个数列的通项公式.
第n项an
序号n
五、数列的通项公式
追问1 :数列的通项公式有什么作用?
根据数列的通项公式可以写出数列的每一项
建构新知
问题 8:数列的单调性是怎样定义的?
事实
下定义
表示方法
性质
特殊元素
建构新知
问题 8:数列的单调性是怎样定义的?
75,87,96,103,110,116,120,128,138,145,153,158,160,162,163,165,168.
建构新知
递减数列:从第2项起,每一项都小于它的前一项的数列
递增数列:从第2项起,每一项都大于它的前一项的数列;
另外:常数列: 各项相等的数列
六、数列的单调性
建构新知
例1 根据下列数列的通项公式,写出数列的前5项,并画出它们的图象.
n 1 2 3 4 5
an
(1)
(2)
n 1 2 3 4 5
an 1 0 -1 0 1
1 3 6 10 15
追问1 :你能判断(1)数列的单调性吗?
巩固应用
例2 . 根据下列数列的前4项,写出数列的一个通项公式:
摆动数列:
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列.
巩固应用
05
课堂小结
1、本节课我们经历了怎样的一个学习数列的过程?
事实
定义
表示方法
性质
特殊元素
2、我们学习了哪些新知识、新的数学思想、方法?
结构再望:除了利用数列的通项公式能写出数列的每一项,还有其他途径吗?
1)数列的概念
2)数列的符号表示
3)数列的分类
(数列是特殊的函数)
4)数列的表示方法
5)数列的通项公式
特殊到一般的思想,类比的方法
课堂小结
基础练习:教材P5 T1 T2
拓展练习:教材P5 T3 T4
课后作业
课 程 结 束
人教A版(2019)高中数学选择性必修二
4.1 数列的概念
第一课时
问题 1:德国天文学家提丢斯 (Titius,1729—1796) 通过对一列数
3,6,12,24,48,96, 192,… 的研究,得出太阳到行星平均距离的经验定律, 他发现: ①后一个数字恰好是前一个数字的 2 倍; ②将 0 加在这列数字的最前面得到,
水星 金星 地球 火星 木星 土星 ......
实际距离 0.39 0.72 1.0 1.52 5.2 9.5 ......
计算距离 ......
0,3,6,12,24,48,96, 192,…
0.4
0.7
1.0
1.6
2.8
5.2
10.0
19.6
(注:表中的数据为天文单位,1个天文单位=太阳到地球的距离)
2.7
19.2
谷神星
天王星
再将每个数字加 4 除以 10,得出另一列数字:
如果你是天文学家,通过这列数,你有什么大胆的猜测?
情景导入
数列
概念
表示
表格
图象
通项公式
递推公式
特殊数列
等差数列
等比数列
类比
概念
前n项和
通项公式
应用
结构导图
问题 2:如何研究“数列”这一新的概念?
事实
定义
表示方法
性质
特殊元素
建构新知—研究路径
(1):王芳从 1 岁到 17 岁每年的身高依次排成一列数:
75,87,96,103,110, 116,120,128,138,145,153,158,160,162,163,165,168. 它们之间能否交换位置?具有确定的顺序吗?
(2):在两河流域发掘的一块泥版上就有一列依次表示一个月中从第 1 天到第 15 天每天月亮可见部分的数:
5,10,20,40,80,96,112,128,144,160,176,192,208,224,240. 它们之间能否交换位置?具有确定的顺序吗?
的n次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数
这也是具有确定顺序的一列数吗?
建构新知—形成概念
一般地,我们把按照确定的顺序排列的一列数称为数列。
数列中的每一个数叫做这个数列的项。
一、数列的概念
追问1: 1,3,5,7 和 7,5,3,1 这两个数列是不是同一个数列?
追问2: 1,1,1,1 是一个数列吗?
问题 4:如何用一般的符号表示数列?
不是
是
建构新知—形成概念
二、数列的符号表示
数列的一般形式:
简记为数列
首项
第2项
第n项
追问:在数列中,符号 所表示的意义是否相同?
问题 5:对于不同的数列,其项数有什么特点?
(1)75,87,96,103,110, 116,120,128,138,145,153,158,160,162,163,165,168.
(2)5,10,20,40,80,96,112,128,144,160,176,192,208,224,240
三、数列的分类
有穷数列:项数有限的数列
无穷数列:项数无限的数列
(3)
建构新知—概念表示
问题 6:数列 中的各项 与各项序号k(k=1,2,3,···,n,···)之间的对应关系是什么关系?
序号
项
函数关系
追问: 和 是同一个数列吗?你能否从函数的角度解释一下?
因为定义域不同,所以它们不是同一个数列。
建构新知—概念辨析
四、数列与函数的关系
数列的定义域是正整数集(或正整数集的有限子集),值域是 R 的子集,
数列是从正整数集(或正整数集的有限子集)到 R 的函数。
问题 7:数列 有哪些表示方法?
事实
定义
表示方法
性质
特殊元素
:列表法、图像法、解析式法
建构新知
问题 7:数列 有哪些表示方法?
列表法、图像法、解析式法
75,87,96,103,110,116,120,128,138,145,153,158,160,162,163,165,168.
建构新知
追问1 :数列的图像有什么特点?
75,87,96,103,110,116,120,128,138,145,153,158,160,162,163,165,168.
追问2:类比函数的解析式,数列有怎样的解析式呢?
数列的图像是由一系列离散的点构成的。
为什么?
建构新知
如果数列{an}的_________与它的________之间的对应关系可以用一个式子来表示,那么这个式子就是数列的函数解析式,叫做这个数列的通项公式.
第n项an
序号n
五、数列的通项公式
追问1 :数列的通项公式有什么作用?
根据数列的通项公式可以写出数列的每一项
建构新知
问题 8:数列的单调性是怎样定义的?
事实
下定义
表示方法
性质
特殊元素
建构新知
问题 8:数列的单调性是怎样定义的?
75,87,96,103,110,116,120,128,138,145,153,158,160,162,163,165,168.
建构新知
递减数列:从第2项起,每一项都小于它的前一项的数列
递增数列:从第2项起,每一项都大于它的前一项的数列;
另外:常数列: 各项相等的数列
六、数列的单调性
建构新知
例1 根据下列数列的通项公式,写出数列的前5项,并画出它们的图象.
n 1 2 3 4 5
an
(1)
(2)
n 1 2 3 4 5
an 1 0 -1 0 1
1 3 6 10 15
追问1 :你能判断(1)数列的单调性吗?
巩固应用
例2 . 根据下列数列的前4项,写出数列的一个通项公式:
摆动数列:
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列.
巩固应用
05
课堂小结
1、本节课我们经历了怎样的一个学习数列的过程?
事实
定义
表示方法
性质
特殊元素
2、我们学习了哪些新知识、新的数学思想、方法?
结构再望:除了利用数列的通项公式能写出数列的每一项,还有其他途径吗?
1)数列的概念
2)数列的符号表示
3)数列的分类
(数列是特殊的函数)
4)数列的表示方法
5)数列的通项公式
特殊到一般的思想,类比的方法
课堂小结
基础练习:教材P5 T1 T2
拓展练习:教材P5 T3 T4
课后作业
课 程 结 束
