四川省巴中市平昌县平昌中学初2021级九上数学第五周课堂练习(无答案)
文档属性
| 名称 | 四川省巴中市平昌县平昌中学初2021级九上数学第五周课堂练习(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 276.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 00:00:00 | ||
图片预览

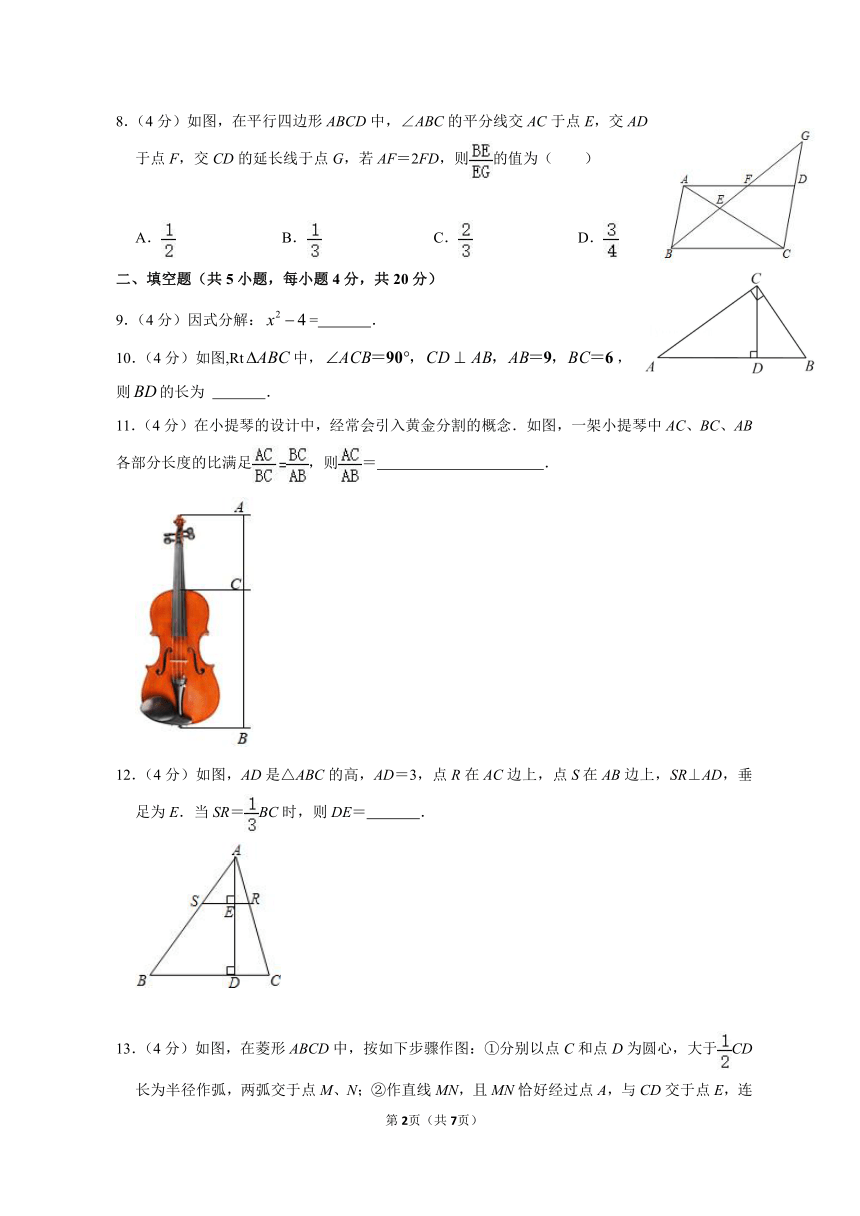
文档简介
四川省巴中市平昌县平昌中学初2021级九上数学第五周课堂练习
A卷(100分)
一、选择题(本大题共8小题,每小题4分,共32分)
1.(4分)下列方程中是一元二次方程的是( )
A.2x+1=0 B.y2+x=1 C.x2+1=0 D.
2.(4分)一元二次方程x2﹣4x+5=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
3.(4分)如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )
A.∠C=∠AED B.∠B=∠D C.= D.=
4.(4分)若把分式中的m、n都扩大到原来的3倍,则分式的值( )
A.扩大9倍 B.扩大6倍 C.扩大3倍 D.不变
5.(4分)同一时刻,同一地点,在阳光下影长为0.4米的小王身高为1.6米,一棵树的影长为3.2米,则这棵树的高度为( )
A.0.8米 B.6.4米 C.12.8米 D.25.6米
6.(4分)如图,已知△ABC与△DEF位似,位似中心为点O,且OA:OD=3:2,则△ABC与△DEF的面积之比为( )
A.3:2 B.3:5 C.9:4 D.9:5
7.(4分)《九章算术》是我国古代数学名著,有题译文如下:今有门,不知其高宽;有竿,不知其长短.横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线长恰好相等.问门高、宽和对角线的长各是多少?设门对角线的长为x尺,下列方程符合题意的是( )
A.(x+2)2+(x﹣4)2=x2 B.(x﹣2)2+(x﹣4)2=x2
C.x2+(x﹣2)2=(x﹣4)2 D.(x﹣2)2+x2=(x+4)2
8.(4分)如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则的值为( )
A. B. C. D.
二、填空题(共5小题,每小题4分,共20分)
9.(4分)因式分解:= .
10.(4分)如图,Rt中,,
则的长为 .
11.(4分)在小提琴的设计中,经常会引入黄金分割的概念.如图,一架小提琴中AC、BC、AB各部分长度的比满足,则= .
12.(4分)如图,AD是△ABC的高,AD=3,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR=BC时,则DE= .
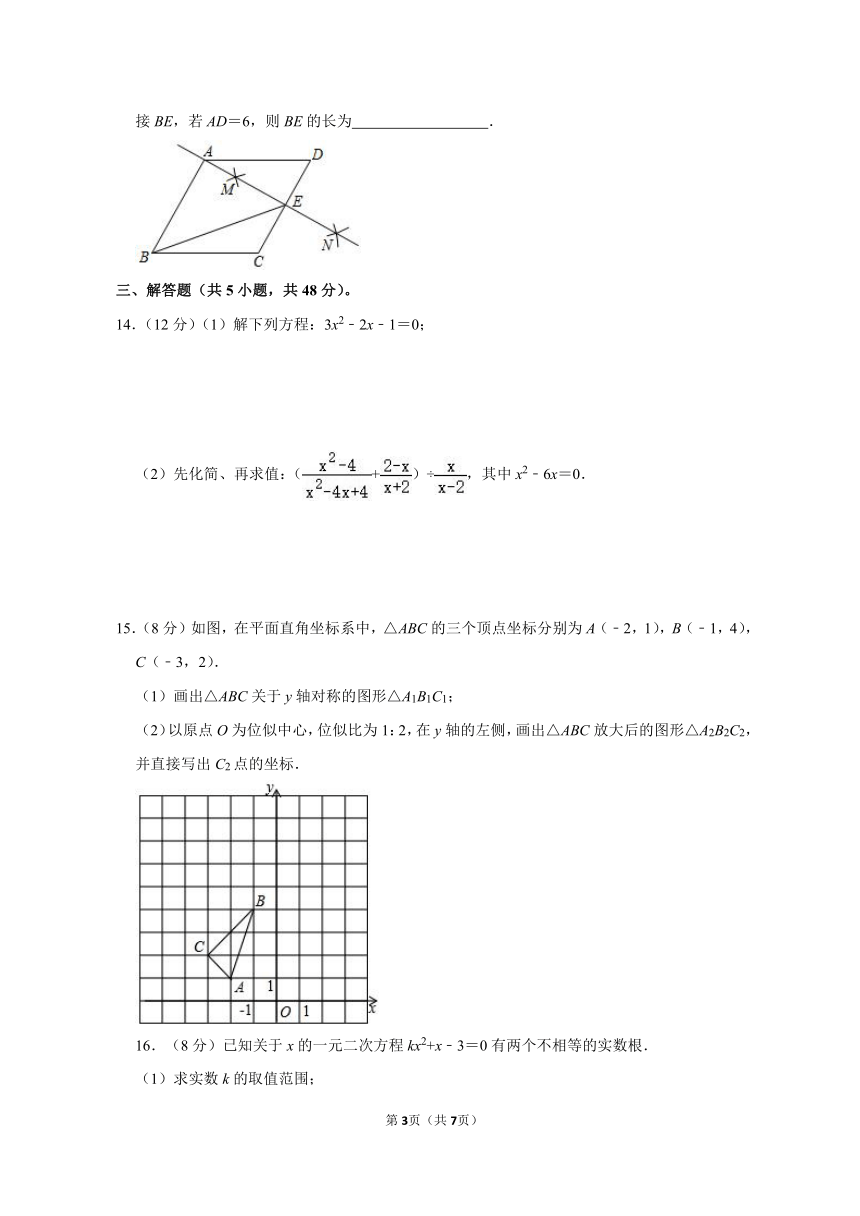
13.(4分)如图,在菱形ABCD中,按如下步骤作图:①分别以点C和点D为圆心,大于CD长为半径作弧,两弧交于点M、N;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,若AD=6,则BE的长为 .
三、解答题(共5小题,共48分)。
14.(12分)(1)解下列方程:3x2﹣2x﹣1=0;
(2)先化简、再求值:(+)÷,其中x2﹣6x=0.
15.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点的坐标.
(8分)已知关于x的一元二次方程kx2+x﹣3=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程两个实数根分别为x1,x2,且满足(x1+x2)2+x1 x2=4,求k的值.
17.(10分)如图,要建一个矩形花圃,花圃的一边利用长为12m的住房墙,另外三边用25m长的篱笆围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,花圃面积为80m2,求与墙垂直的一边的长度.
18.(10分)如图,在四边形中,,分别是边和对角线上的点
⑴如图1,若四边形为正方形,,求证:∽;
⑵如图2,若四边形为矩形,,,,,求的长;
⑶如图3,若四边形为菱形,,,过作交延长线于点,的延长线
交于点,若,,求的长.
B卷(50分)
四、填空题(共5小题,每小题4分,共20分)
19.(4分)若x1,x2是一元二次方程x2+x﹣3=0的两个实数根,则x22﹣x1+2020的值为 .
20.(4分)已知一个直角三角形的两条直角边的长恰好是方程3x2﹣6x+2=0的两个根,则这个直角三角形的斜边长是 .
21.(4分)如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则的值为 .
22.(4分)如图,在矩形ABCD中,AB=2,BC=4,点E是边AD上一动点,EF=2CE,且EF⊥CE,则AF的最小值为 .
23.(4分)如图,在矩形ABCD中,AB=5,AD=10,点E,F分别在边AD,BC上,且AE=4,按以下步骤操作:
第一步,沿直线EF翻折,点A的对应点A'恰好落在对角线AC上,点B的对应点为B',则线段BF的长为 ;
第二步,分别在EF,A'B'上取点M,N,沿直线MN继续翻折,使点F与点E重合,则线段MN的长为 .
五、解答题(共3小题,共30分)
24.(8分)“玫瑰香”葡萄品种是农科院研制的优质新品种,在被广泛种植,某葡萄种植基地2021年种植64亩,到2023年的种植面积达到100亩.
(1)求该基地这两年“玫瑰香”种植面积的平均增长率.
(2)某超市调查发现,当“玫瑰香”的售价为8元/千克时,每周能售出400千克,售价每上涨1元,每周销售量减少20千克,已知该超市“玫瑰香”的进价为6元/千克,为了维护消费者利益,成都市物价部门规定,该水果售价不能超过15元.若使销售“玫瑰香”每周获利2240元,则售价应上涨多少元?
25.(10分)请解答下列各题:
(1)如图1,矩形ABCD中,点E、F分别在AB和BC上,且DF⊥CE,垂足G,求证:=.
(2)如图2,若四边形ABCD是平行四边形.试探究:当∠B与∠EGC满足什么关系时,使得=成立?并证明你的结论.
(3)如图3,若BA=BC=2,DA=DC=,∠BAD=90°,DE⊥CF.请直接写出的值.
26.(12分)如图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求直线CD的函数解析式;
(2)在直线AB上是否存在一点P,使得△PBO与△ADC相似?若存在,求点P的坐标;若不存在,
请说明理由;
(3)现定义:平面内一点到三角形三边所在的直线距离之和等于该三角形周长的一半时,这个点称
为此三角形的和谐点.在直线AD上是否存在△COD的和谐点,若存在请求出和谐点的坐标;若不存在,
请说明理由.
图1
图2
图3
第6页(共7页)
A卷(100分)
一、选择题(本大题共8小题,每小题4分,共32分)
1.(4分)下列方程中是一元二次方程的是( )
A.2x+1=0 B.y2+x=1 C.x2+1=0 D.
2.(4分)一元二次方程x2﹣4x+5=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
3.(4分)如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )
A.∠C=∠AED B.∠B=∠D C.= D.=
4.(4分)若把分式中的m、n都扩大到原来的3倍,则分式的值( )
A.扩大9倍 B.扩大6倍 C.扩大3倍 D.不变
5.(4分)同一时刻,同一地点,在阳光下影长为0.4米的小王身高为1.6米,一棵树的影长为3.2米,则这棵树的高度为( )
A.0.8米 B.6.4米 C.12.8米 D.25.6米
6.(4分)如图,已知△ABC与△DEF位似,位似中心为点O,且OA:OD=3:2,则△ABC与△DEF的面积之比为( )
A.3:2 B.3:5 C.9:4 D.9:5
7.(4分)《九章算术》是我国古代数学名著,有题译文如下:今有门,不知其高宽;有竿,不知其长短.横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线长恰好相等.问门高、宽和对角线的长各是多少?设门对角线的长为x尺,下列方程符合题意的是( )
A.(x+2)2+(x﹣4)2=x2 B.(x﹣2)2+(x﹣4)2=x2
C.x2+(x﹣2)2=(x﹣4)2 D.(x﹣2)2+x2=(x+4)2
8.(4分)如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则的值为( )
A. B. C. D.
二、填空题(共5小题,每小题4分,共20分)
9.(4分)因式分解:= .
10.(4分)如图,Rt中,,
则的长为 .
11.(4分)在小提琴的设计中,经常会引入黄金分割的概念.如图,一架小提琴中AC、BC、AB各部分长度的比满足,则= .
12.(4分)如图,AD是△ABC的高,AD=3,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR=BC时,则DE= .
13.(4分)如图,在菱形ABCD中,按如下步骤作图:①分别以点C和点D为圆心,大于CD长为半径作弧,两弧交于点M、N;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,若AD=6,则BE的长为 .
三、解答题(共5小题,共48分)。
14.(12分)(1)解下列方程:3x2﹣2x﹣1=0;
(2)先化简、再求值:(+)÷,其中x2﹣6x=0.
15.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点的坐标.
(8分)已知关于x的一元二次方程kx2+x﹣3=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程两个实数根分别为x1,x2,且满足(x1+x2)2+x1 x2=4,求k的值.
17.(10分)如图,要建一个矩形花圃,花圃的一边利用长为12m的住房墙,另外三边用25m长的篱笆围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,花圃面积为80m2,求与墙垂直的一边的长度.
18.(10分)如图,在四边形中,,分别是边和对角线上的点
⑴如图1,若四边形为正方形,,求证:∽;
⑵如图2,若四边形为矩形,,,,,求的长;
⑶如图3,若四边形为菱形,,,过作交延长线于点,的延长线
交于点,若,,求的长.
B卷(50分)
四、填空题(共5小题,每小题4分,共20分)
19.(4分)若x1,x2是一元二次方程x2+x﹣3=0的两个实数根,则x22﹣x1+2020的值为 .
20.(4分)已知一个直角三角形的两条直角边的长恰好是方程3x2﹣6x+2=0的两个根,则这个直角三角形的斜边长是 .
21.(4分)如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则的值为 .
22.(4分)如图,在矩形ABCD中,AB=2,BC=4,点E是边AD上一动点,EF=2CE,且EF⊥CE,则AF的最小值为 .
23.(4分)如图,在矩形ABCD中,AB=5,AD=10,点E,F分别在边AD,BC上,且AE=4,按以下步骤操作:
第一步,沿直线EF翻折,点A的对应点A'恰好落在对角线AC上,点B的对应点为B',则线段BF的长为 ;
第二步,分别在EF,A'B'上取点M,N,沿直线MN继续翻折,使点F与点E重合,则线段MN的长为 .
五、解答题(共3小题,共30分)
24.(8分)“玫瑰香”葡萄品种是农科院研制的优质新品种,在被广泛种植,某葡萄种植基地2021年种植64亩,到2023年的种植面积达到100亩.
(1)求该基地这两年“玫瑰香”种植面积的平均增长率.
(2)某超市调查发现,当“玫瑰香”的售价为8元/千克时,每周能售出400千克,售价每上涨1元,每周销售量减少20千克,已知该超市“玫瑰香”的进价为6元/千克,为了维护消费者利益,成都市物价部门规定,该水果售价不能超过15元.若使销售“玫瑰香”每周获利2240元,则售价应上涨多少元?
25.(10分)请解答下列各题:
(1)如图1,矩形ABCD中,点E、F分别在AB和BC上,且DF⊥CE,垂足G,求证:=.
(2)如图2,若四边形ABCD是平行四边形.试探究:当∠B与∠EGC满足什么关系时,使得=成立?并证明你的结论.
(3)如图3,若BA=BC=2,DA=DC=,∠BAD=90°,DE⊥CF.请直接写出的值.
26.(12分)如图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求直线CD的函数解析式;
(2)在直线AB上是否存在一点P,使得△PBO与△ADC相似?若存在,求点P的坐标;若不存在,
请说明理由;
(3)现定义:平面内一点到三角形三边所在的直线距离之和等于该三角形周长的一半时,这个点称
为此三角形的和谐点.在直线AD上是否存在△COD的和谐点,若存在请求出和谐点的坐标;若不存在,
请说明理由.
图1
图2
图3
第6页(共7页)
同课章节目录
