反比例函数(江苏省徐州市贾汪区)

课件20张PPT。贾汪区建平求知中学
李孝勤旧知回顾什么是函数? 一般地,设在一个变化的过程中有两个
x和y，如果对于变量x的每一个值，变量y都
有 的值与它对应，我们称y是x的函数 .其
中，x是自变量，y是 因变量。变量唯一一次函数：y=kx+b k≠0正比例函数： y=kx k≠0
9.1 反比例函数教学目标：
1、 理解反比例函数的概念，能判断两个变量之间的关系是否是函数关系，进而识别其中的反比例函数.
2、 能根据实际问题中的条件确定反比例函数的关系式.
3、 通过探索现实生活中数量间的反比例关系，体会和认识反比例函数是刻画现实世界中特定数量关系的一种数学模型；想一想 汽车从南京出发开往上海（全程约300km），全程所用时间t（h）随速度v（km/h）的变化而变化.
问题：（1）你能用含有v的代数式表示t吗？
（2）利用（1）的关系式完成下表：
（3）随着速度的变化，全程所用时间发生怎样的变化？
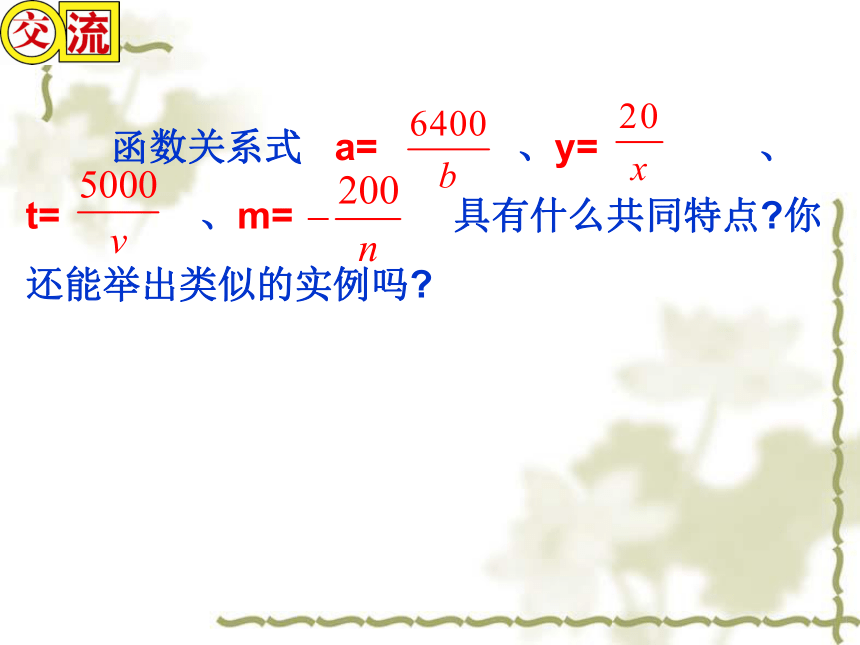
（4）时间t是速度v的函数吗？为什么？ 53 用函数关系式表示下列问题中两个变量之间的关系: (1)一个面积为6400㎡的长方形的长a(m)随宽b(m)的变化而变化; (2)某银行为资助某社会福利厂,提供了20万元的无息贷款,该厂的平均年还贷额y(万元)随还款年限x(年)的变化而变化; (3)游泳池的容积为5000m3,向池内注水,注满水所需时间t(h)随注水速度v(m3／h)的变化而变化; (4)实数m与n的积为-200,m随n的变化而变化. 函数关系式 a= 、y= 、
t= 、m= 具有什么共同特点?你
还能举出类似的实例吗?什么是反比例函数? 一般地,形如 (k为常数,k≠0)的函数称
为反比例函数,其中x是自变量,y是x的反比例函数,k是比例系数.反比例函数的自变量x的取值范围是不等于0的一切实数.下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?(1) ; (2) ; (3) y=1-x ; (4) xy=1 ; (5) ； (6) y=-3x例 题-1注意:2.反比例函数也可以表示为y=kx-1(k为 常数,k≠0)的形式.1.反比例函数可以表示为 xy=k(k为 常数,k≠0)的形式.互动平台 每人写三个反比例函数，请同桌指出其中k的值。
练一练1、写出下列问题中两个变量之间的函数关系式，并判断其是否为反比例函数. 如果是，指出比例系数k的值.
（1）底边为5cm的三角形的面积y（cm2）随底边上的高 x（cm）的变化而变化；
（2）某村有耕地面积200ha，人均占有耕地面积y（ha）随人口数量x（人）的变化而变化；
（3）一个物体重120N，物体对地面的压强p（N/m2）随该物体与地面的接触面积S（m2）的变化而变化.
（4）矩形的面积为4，一条边的长x，随另一条边的长y的变化而变化⑴ 在下列函数中，y是x的反比例函数的是（ ）
（A） （B） + 7
（C）xy = 5 （D）
⑵ 已知函数 是正比例函数,则 m = ___ ；

已知函数 是反比例函数,则 m = ___ 。C86练一练
2．已知y与x成反比例，且当x＝－2时，y＝3，则y与x之间的函数关系式
是 ，
当x＝－3时，y＝
练一练 2利用概念解题 当m为何值时，函数 是反比例函数，并求出其函数解析式． 解：由反比例函数的定义得：生 活 应 用你能利用反比例函数 表示生活中的数量关系吗？ 例如：小明的家距离学校4千米，早晨小明骑自行车上学需x小时，那么小明骑车的速度为每小时y千米，则速度y可以表示为你还能举出这样的一些实际例子吗？本节课，我学到了哪些知识？
本节课，给我感受最深的是什么？
此外我还知道了……
感悟教师感言 时间是一个“常量”，但对于勤奋者来说，却是一个“变量”，我们应当在有限的时间内做出伟大的事业！作业1、书本 P64 1 、2 再 见！