3.4 函数的应用(一) 课件(共23张PPT)
文档属性
| 名称 | 3.4 函数的应用(一) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 17:44:21 | ||
图片预览








文档简介
(共23张PPT)
3.4 函数的应用
第三章 函数的概念与性质
情境引入
很多人对数学的刻板印象就是——枯燥无味,对以后的生活没有太大的用处.其实数学是我们生活的一部分,数学最开始也是满足生活的需要不断前进发展的.当你用手机支付完成一次付款,当你面对高楼大厦,当你看到神舟系列飞船成功发射,这些都离不开数学和数学模型.
我们学习过的一次函数、二次函数、幂函数等都与现实世界有紧密联系.下面通过一些实例感受它们的广泛应用,体会利用函数模型解决实际问题的过程与方法.
例析
例1.设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额与3.1.2例8相同,全年综合所得收入额为(单位:元),应缴纳综合所得个税税额为(单位:元).
(1)求关于的函数解析式;
(2)如果小王全年的综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税?
级数 全年应纳税所得额所在区间 税率 (0/0) 速算扣除数
1 [0,36000] 3 0
2 (36000,144000] 10 2520
3 (144000,300000] 20 16920
4 (300000,420000] 25 31920
5 (420000,660000] 30 52920
6 (660000,960000] 35 85920
7 (960000,+∞) 45 181920
例析
例1.设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额与3.1.2例8相同,全年综合所得收入额为(单位:元),应缴纳综合所得个税税额为(单位:元).
(1)求关于的函数解析式;
级数 全年应纳税所得额所在区间 税率 (0/0) 速算扣除数
1 [0,36000] 3 0
2 (36000,144000] 10 2520
3 (144000,300000] 20 16920
4 (300000,420000] 25 31920
5 (420000,660000] 30 52920
6 (660000,960000] 35 85920
7 (960000,+∞) 45 181920
解:由个人应缴纳所得额计算公式,可得:
令0,得
根据个人应纳税所得额的规定可知,当时,0.所以,个人应纳税所得额关于综合所得额的函数解析式为
,,
,
例析
结合3.1.2例8的解析式③,可得:
当时,0,所以;
当时,0,
所以;
当时,0,
所以;
当时,0,
所以;
当时,0,
所以;
当时,0,
所以;
例析
当时,0,
所以;
当时,0,
所以
所以,函数解析式为
,
④
例析
(2)如果小王全年的综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税?
解:根据④,当时,
所以,小王全年应缴纳5721元的综合所得个税.
例析
例2.一辆汽车在某段路程中行驶的平均速率与时间的关系如图所示,
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
解:阴影部分的面积为:
801+901+751+65
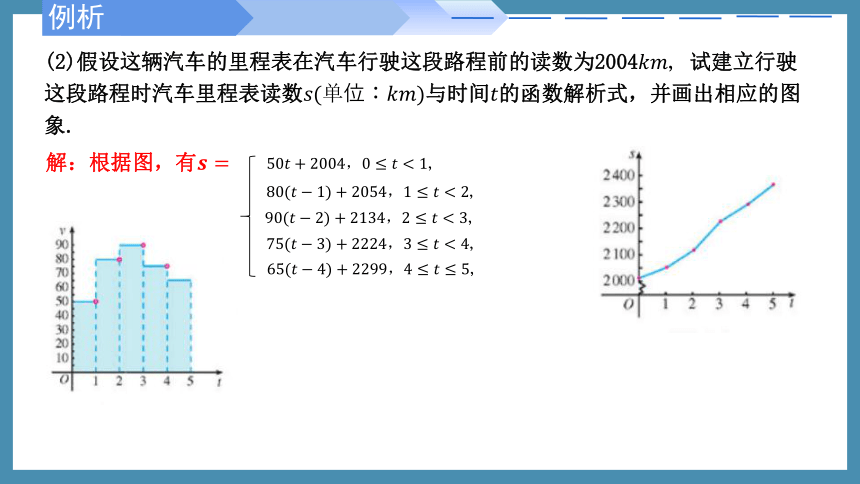
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004试建立行驶这段路程时汽车里程表读数与时间的函数解析式,并画出相应的图象.
例析
解:根据图,有
练习
例1.某区广场车管站在某个星期日保管的自行车和电动车共有辆次,其中电动车保管费是每辆一次元,自行车保管费一次元.
(1)若设自行车和电动车停放的辆次依次为和,保管费收入依次为和元,试写出与的函数关系式.
(2)若估计前来停放的4000辆次自行车和电动车中,电动车的辆次数不小于45%,但不大于60%,试求该车管站这个星期日电动车收入保管费的范围.
答案:(1)
(2)的值域是
即收入在1225元至1330元之间.
题型一:一次函数模型
练习
例1.某区广场车管站在某个星期日保管的自行车和电动车共有辆次,其中电动车保管费是每辆一次元,自行车保管费一次元.
(1)若设自行车停放的辆次为,保管费收入依次为元,试写出与的函数关系式;
题型一:一次函数模型
解(1):
练习
例1.某区广场车管站在某个星期日保管的自行车和电动车共有辆次,其中电动车保管费是每辆一次元,自行车保管费一次元.
(2)若估计前来停放的4000辆次自行车和电动车中,电动车的辆次数不小于45%,但不大于60%,试求该车管站这个星期日收入保管费总数的范围.
解(2):∵
∴函数在上单调递减,
∴值域是
即收入在元至元之间.
练习
方法技巧:
解决一次函数模型应用题的四个步骤:
(1)审题:理解题意,设定变量.
(2)建模:建立一次函数关系,并注明定义域.
(3)解模:运用一次函数相关知识求解.
(4)结论:回归到应用问题中去,给出答案.
练习
题型二:二次函数模型
例2.大理欧亚牧场蓄养了很多奶牛以满足大理市市民们的奶制品需求.已知欧亚牧场中牛群的最大蓄养量为只,为保证牛群的生长空间,实际蓄养量不能达到最大蓄养量,必须留出适当的空闲率.已知牛群的年增长量只和实际蓄养量只与空闲率的乘积成正比,正比系数为.
(1)写出关于的函数关系式,并指出这个函数的定义域;
解(1):据题意,由于最大蓄养量为只,实际蓄养量为只,则蓄养率为,
故空闲率为,由此可得.
练习
例2.大理欧亚牧场蓄养了很多奶牛以满足大理市市民们的奶制品需求.已知欧亚牧场中牛群的最大蓄养量为只,为保证牛群的生长空间,实际蓄养量不能达到最大蓄养量,必须留出适当的空闲率.已知牛群的年增长量只和实际蓄养量只与空闲率的乘积成正比,正比系数为.
(2)求牛群年增长量的最大值;
解(2):∵.
即当时,取得最大值.
练习
例2.大理欧亚牧场蓄养了很多奶牛以满足大理市市民们的奶制品需求.已知欧亚牧场中牛群的最大蓄养量为只,为保证牛群的生长空间,实际蓄养量不能达到最大蓄养量,必须留出适当的空闲率.已知牛群的年增长量只和实际蓄养量只与空闲率的乘积成正比,正比系数为.
(3)当牛群的年增长量达到最大值时,求的取值范围.
解(3):由题意知为给牛群留有一定的生长空间,则有实际蓄养量与年增长量的和小于最大蓄养量,即.
∵当时,,所以,解得.
又∵,∴.故的取值范围为.
练习
方法技巧:
解决二次函数模型应用题的四个步骤:
(1)审题:理解题意,设定变量,.
(2)建模:建立二次函数关系,并注明定义域.
(3)解模:运用二次函数相关知识求解.
(4)结论:回归到应用问题中去,给出答案.
练习
题型三:幂函数模型
例3.包装的一个知识,大包装商品的成本要比小包装商品的成本低.某种品牌的薯片其36克装的售价为4元,其100克装的售价为元,假定该薯片的售价由三部分组成:生产成本、包装成本、利润.生产成本与薯片质量成正比且系数为,包装成本与薯片质量的算术平方根成正比且系数为,利润率为20%,试写出该种饼干200克装的合理售价.
解:设薯片的质量为克,则其售价(单位:元)与之间的函数解析式为
.由题意得:,即①
即②由①②解得,.
∴.当时,.
故这种200克薯片的合理售价为.
练习
方法技巧:
解决幂函数模型应用题的步骤:
首先根据题中的关系建立模型,然后再根据已知数据求解模型中的参数,最后得出结论.
练习
题型四:分段函数模型
例4.已知某商品在近30天内每件的销售价格(元)与时间(天)的函数关系是
该商品的日销量(件)与时间(天)的函数
关系是
(1)写出该种商品的日销售额(元)与时间(天)的函数关系式;
(2)求日销量额的最大值.
答案:
(2)第25天时,日销售额最大,是1200元.
练习
方法技巧:
解决分段函数模型应用题的步骤:
首先根据题中的关系建立模型,然后再根据已知数据求解模型中的参数,利用分段函数通过相关函数类型求最值或值域的方法,最后得出结论.
课堂小结&作业
小结
数学建模解模的过程:
提炼
问题
收集数据
收集数据
建立函数模型
求模、
检验还原
作业:
1.课本的练习1——3题;
2.课本,习题3.4的练习1——4题.
谢谢学习
Thank you for learning
3.4 函数的应用
第三章 函数的概念与性质
情境引入
很多人对数学的刻板印象就是——枯燥无味,对以后的生活没有太大的用处.其实数学是我们生活的一部分,数学最开始也是满足生活的需要不断前进发展的.当你用手机支付完成一次付款,当你面对高楼大厦,当你看到神舟系列飞船成功发射,这些都离不开数学和数学模型.
我们学习过的一次函数、二次函数、幂函数等都与现实世界有紧密联系.下面通过一些实例感受它们的广泛应用,体会利用函数模型解决实际问题的过程与方法.
例析
例1.设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额与3.1.2例8相同,全年综合所得收入额为(单位:元),应缴纳综合所得个税税额为(单位:元).
(1)求关于的函数解析式;
(2)如果小王全年的综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税?
级数 全年应纳税所得额所在区间 税率 (0/0) 速算扣除数
1 [0,36000] 3 0
2 (36000,144000] 10 2520
3 (144000,300000] 20 16920
4 (300000,420000] 25 31920
5 (420000,660000] 30 52920
6 (660000,960000] 35 85920
7 (960000,+∞) 45 181920
例析
例1.设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额与3.1.2例8相同,全年综合所得收入额为(单位:元),应缴纳综合所得个税税额为(单位:元).
(1)求关于的函数解析式;
级数 全年应纳税所得额所在区间 税率 (0/0) 速算扣除数
1 [0,36000] 3 0
2 (36000,144000] 10 2520
3 (144000,300000] 20 16920
4 (300000,420000] 25 31920
5 (420000,660000] 30 52920
6 (660000,960000] 35 85920
7 (960000,+∞) 45 181920
解:由个人应缴纳所得额计算公式,可得:
令0,得
根据个人应纳税所得额的规定可知,当时,0.所以,个人应纳税所得额关于综合所得额的函数解析式为
,,
,
例析
结合3.1.2例8的解析式③,可得:
当时,0,所以;
当时,0,
所以;
当时,0,
所以;
当时,0,
所以;
当时,0,
所以;
当时,0,
所以;
例析
当时,0,
所以;
当时,0,
所以
所以,函数解析式为
,
④
例析
(2)如果小王全年的综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税?
解:根据④,当时,
所以,小王全年应缴纳5721元的综合所得个税.
例析
例2.一辆汽车在某段路程中行驶的平均速率与时间的关系如图所示,
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
解:阴影部分的面积为:
801+901+751+65
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004试建立行驶这段路程时汽车里程表读数与时间的函数解析式,并画出相应的图象.
例析
解:根据图,有
练习
例1.某区广场车管站在某个星期日保管的自行车和电动车共有辆次,其中电动车保管费是每辆一次元,自行车保管费一次元.
(1)若设自行车和电动车停放的辆次依次为和,保管费收入依次为和元,试写出与的函数关系式.
(2)若估计前来停放的4000辆次自行车和电动车中,电动车的辆次数不小于45%,但不大于60%,试求该车管站这个星期日电动车收入保管费的范围.
答案:(1)
(2)的值域是
即收入在1225元至1330元之间.
题型一:一次函数模型
练习
例1.某区广场车管站在某个星期日保管的自行车和电动车共有辆次,其中电动车保管费是每辆一次元,自行车保管费一次元.
(1)若设自行车停放的辆次为,保管费收入依次为元,试写出与的函数关系式;
题型一:一次函数模型
解(1):
练习
例1.某区广场车管站在某个星期日保管的自行车和电动车共有辆次,其中电动车保管费是每辆一次元,自行车保管费一次元.
(2)若估计前来停放的4000辆次自行车和电动车中,电动车的辆次数不小于45%,但不大于60%,试求该车管站这个星期日收入保管费总数的范围.
解(2):∵
∴函数在上单调递减,
∴值域是
即收入在元至元之间.
练习
方法技巧:
解决一次函数模型应用题的四个步骤:
(1)审题:理解题意,设定变量.
(2)建模:建立一次函数关系,并注明定义域.
(3)解模:运用一次函数相关知识求解.
(4)结论:回归到应用问题中去,给出答案.
练习
题型二:二次函数模型
例2.大理欧亚牧场蓄养了很多奶牛以满足大理市市民们的奶制品需求.已知欧亚牧场中牛群的最大蓄养量为只,为保证牛群的生长空间,实际蓄养量不能达到最大蓄养量,必须留出适当的空闲率.已知牛群的年增长量只和实际蓄养量只与空闲率的乘积成正比,正比系数为.
(1)写出关于的函数关系式,并指出这个函数的定义域;
解(1):据题意,由于最大蓄养量为只,实际蓄养量为只,则蓄养率为,
故空闲率为,由此可得.
练习
例2.大理欧亚牧场蓄养了很多奶牛以满足大理市市民们的奶制品需求.已知欧亚牧场中牛群的最大蓄养量为只,为保证牛群的生长空间,实际蓄养量不能达到最大蓄养量,必须留出适当的空闲率.已知牛群的年增长量只和实际蓄养量只与空闲率的乘积成正比,正比系数为.
(2)求牛群年增长量的最大值;
解(2):∵.
即当时,取得最大值.
练习
例2.大理欧亚牧场蓄养了很多奶牛以满足大理市市民们的奶制品需求.已知欧亚牧场中牛群的最大蓄养量为只,为保证牛群的生长空间,实际蓄养量不能达到最大蓄养量,必须留出适当的空闲率.已知牛群的年增长量只和实际蓄养量只与空闲率的乘积成正比,正比系数为.
(3)当牛群的年增长量达到最大值时,求的取值范围.
解(3):由题意知为给牛群留有一定的生长空间,则有实际蓄养量与年增长量的和小于最大蓄养量,即.
∵当时,,所以,解得.
又∵,∴.故的取值范围为.
练习
方法技巧:
解决二次函数模型应用题的四个步骤:
(1)审题:理解题意,设定变量,.
(2)建模:建立二次函数关系,并注明定义域.
(3)解模:运用二次函数相关知识求解.
(4)结论:回归到应用问题中去,给出答案.
练习
题型三:幂函数模型
例3.包装的一个知识,大包装商品的成本要比小包装商品的成本低.某种品牌的薯片其36克装的售价为4元,其100克装的售价为元,假定该薯片的售价由三部分组成:生产成本、包装成本、利润.生产成本与薯片质量成正比且系数为,包装成本与薯片质量的算术平方根成正比且系数为,利润率为20%,试写出该种饼干200克装的合理售价.
解:设薯片的质量为克,则其售价(单位:元)与之间的函数解析式为
.由题意得:,即①
即②由①②解得,.
∴.当时,.
故这种200克薯片的合理售价为.
练习
方法技巧:
解决幂函数模型应用题的步骤:
首先根据题中的关系建立模型,然后再根据已知数据求解模型中的参数,最后得出结论.
练习
题型四:分段函数模型
例4.已知某商品在近30天内每件的销售价格(元)与时间(天)的函数关系是
该商品的日销量(件)与时间(天)的函数
关系是
(1)写出该种商品的日销售额(元)与时间(天)的函数关系式;
(2)求日销量额的最大值.
答案:
(2)第25天时,日销售额最大,是1200元.
练习
方法技巧:
解决分段函数模型应用题的步骤:
首先根据题中的关系建立模型,然后再根据已知数据求解模型中的参数,利用分段函数通过相关函数类型求最值或值域的方法,最后得出结论.
课堂小结&作业
小结
数学建模解模的过程:
提炼
问题
收集数据
收集数据
建立函数模型
求模、
检验还原
作业:
1.课本的练习1——3题;
2.课本,习题3.4的练习1——4题.
谢谢学习
Thank you for learning
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
