机械效率课后练习1
图片预览

文档简介
机械效率课后练习(上)
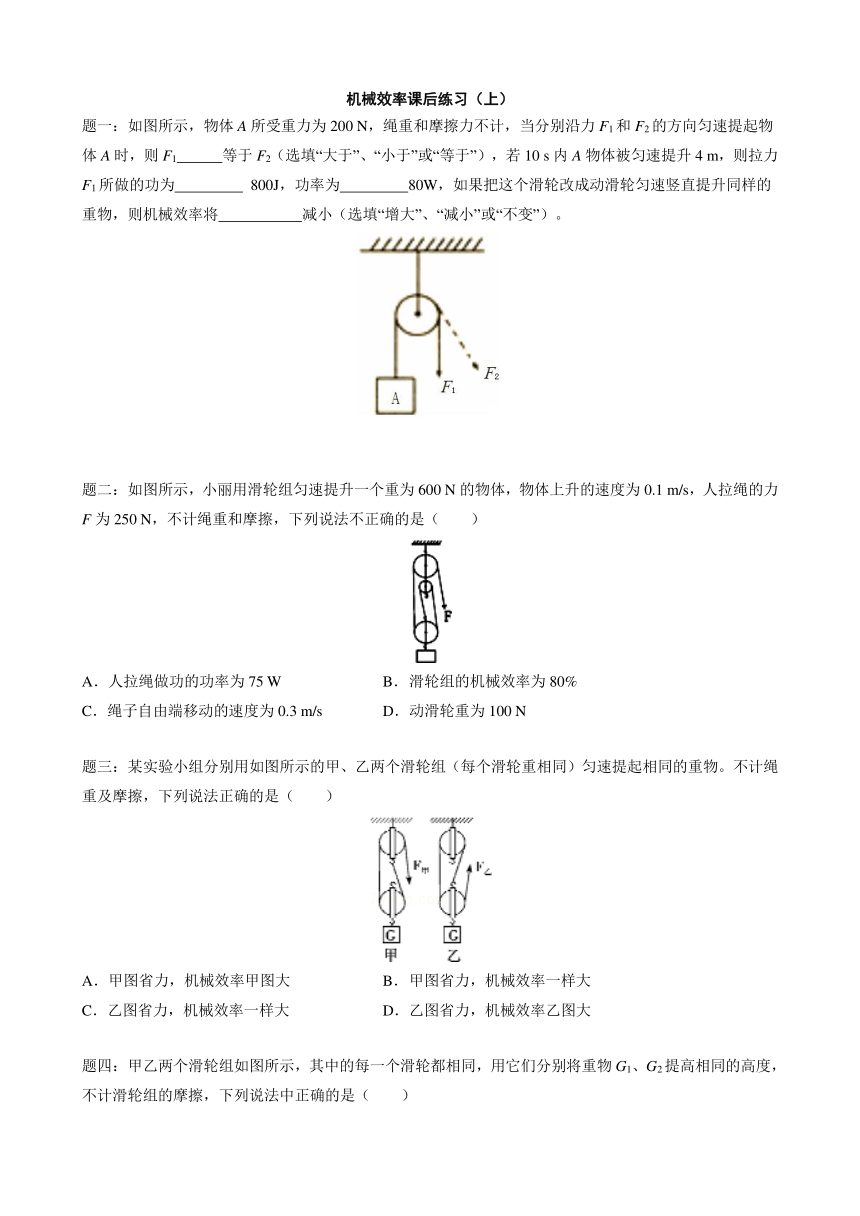
如图所示,物体A所受重力为200 N,绳重和摩擦力不计,当分别沿力F1和F2的方向匀速提起物体A时,则F1 等于F2(选填“大于”、“小于”或“等于”),若10 s内A物体被匀速提升4 m,则拉力F1所做的功为 800J,功率为 80W,如果把这个滑轮改成动滑轮匀速竖直提升同样的重物,则机械效率将 减小(选填“增大”、“减小”或“不变”)。
如图所示,小丽用滑轮组匀速提升一个重为600 N的物体,物体上升的速度为0.1 m/s,人拉绳的力F为250 N,不计绳重和摩擦,下列说法不正确的是( )
A.人拉绳做功的功率为75 W B. 滑轮组的机械效率为80%
C.绳子自由端移动的速度为0.3 m/s D. 动滑轮重为100 N
某实验小组分别用如图所示的甲、乙两个滑轮组(每个滑轮重相同)匀速提起相同的重物。不计绳重及摩擦,下列说法正确的是( )
A.甲图省力,机械效率甲图大 B. 甲图省力,机械效率一样大
C.乙图省力,机械效率一样大 D. 乙图省力,机械效率乙图大
甲乙两个滑轮组如图所示,其中的每一个滑轮都相同,用它们分别将重物G1、G2提高相同的高度,不计滑轮组的摩擦,下列说法中正确的是( )
A.若G1=G2,拉力做的额外功相同
B.若G1=G2,拉力做的总功相同
C.若G1=G2,甲的机械效率大于乙的机械效率
D.用甲乙其中的任何一个滑轮组提起不同的重物,机械效率不变
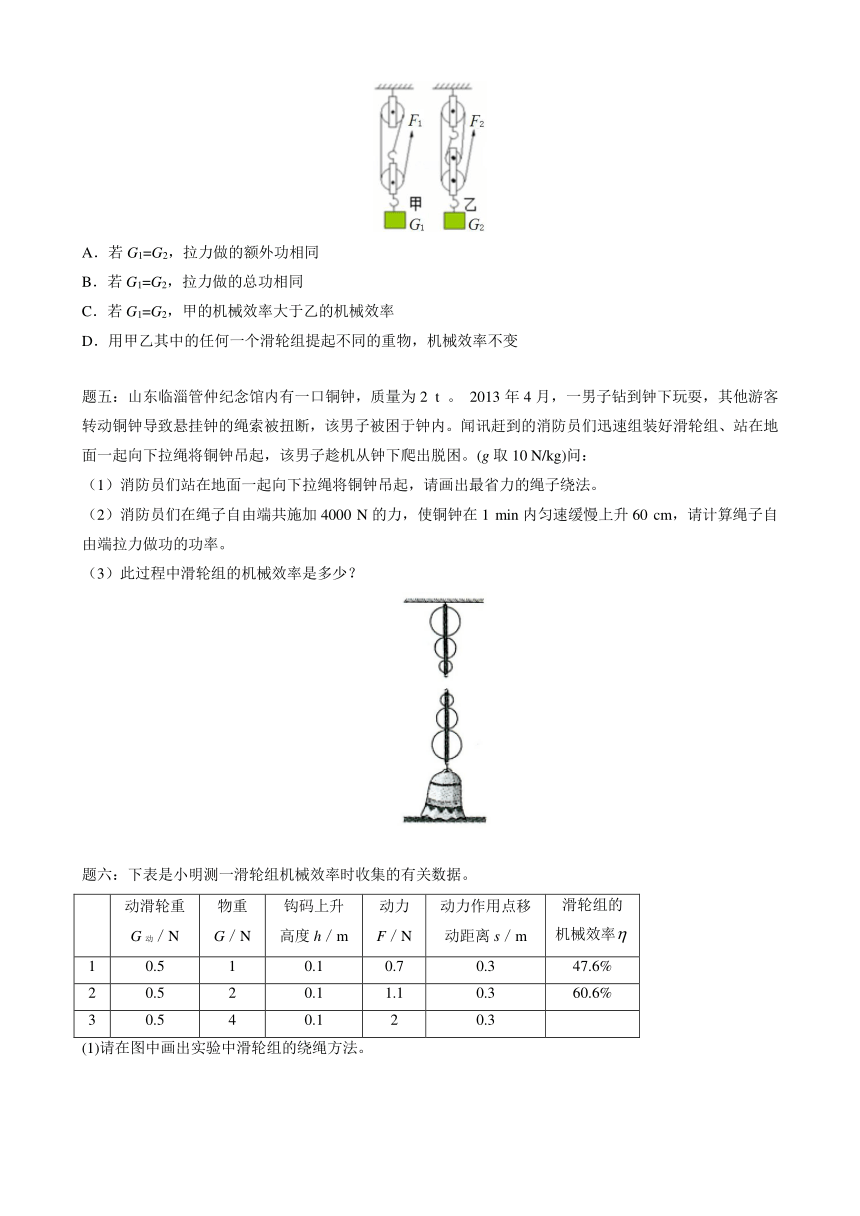
山东临淄管仲纪念馆内有一口铜钟,质量为2 t 。 2013年4月,一男子钻到钟下玩耍,其他游客转动铜钟导致悬挂钟的绳索被扭断,该男子被困于钟内。闻讯赶到的消防员们迅速组装好滑轮组、站在地面一起向下拉绳将铜钟吊起,该男子趁机从钟下爬出脱困。(g取10 N/kg)问:
(1)消防员们站在地面一起向下拉绳将铜钟吊起,请画出最省力的绳子绕法。
(2)消防员们在绳子自由端共施加4000 N的力,使铜钟在1 min内匀速缓慢上升60 cm,请计算绳子自由端拉力做功的功率。
(3)此过程中滑轮组的机械效率是多少?
下表是小明测一滑轮组机械效率时收集的有关数据。
动滑轮重
G动/N
物重
G/N
钩码上升
高度h/m
动力
F/N
动力作用点移
动距离s/m
滑轮组的
机械效率
1
0.5
1
0.1
0.7
0.3
47.6%
2
0.5
2
0.1
1.1
0.3
60.6%
3
0.5
4
0.1
2
0.3
(1)请在图中画出实验中滑轮组的绕绳方法。
(2)将表格中的数据补充完整。
(3)用同一滑轮组提升不同重物至同一高度,提升的物重增加时,除克服动滑轮重所做的额外功外,其它额外功将_________ (选填“变大”、“变小”或“不变”)。进一步分析可知,在动滑轮和绳重一定的情况下,该滑轮组的机械效率与_________和_________有关。
(4)第一次实验中,钩码上升0.1 m所用的时间为1.5 s ,则动力的功率为_________W。
如图所示,利用轻质滑轮组匀速拉动水平地面上重为300 N的物体,拉力F的大小为30 N。若物体和地面之间的摩擦力大小为45 N,则A处的拉力大小和滑轮组的机械效率分别为( )
A.45N、50% B.45 N、75% C.60 N、50% D.60 N、75%
(多选)如图所示,在水平拉力F的作用下,使物体A沿水平面以速度v向右匀速运动了距离s,若物重为G,平面对物体的摩擦力为f。下列说法正确的是( )
A.有用功的功率为fv B.拉力的功率为3Fv
C.装置的机械效率为 D.额外功为(3F-f)s
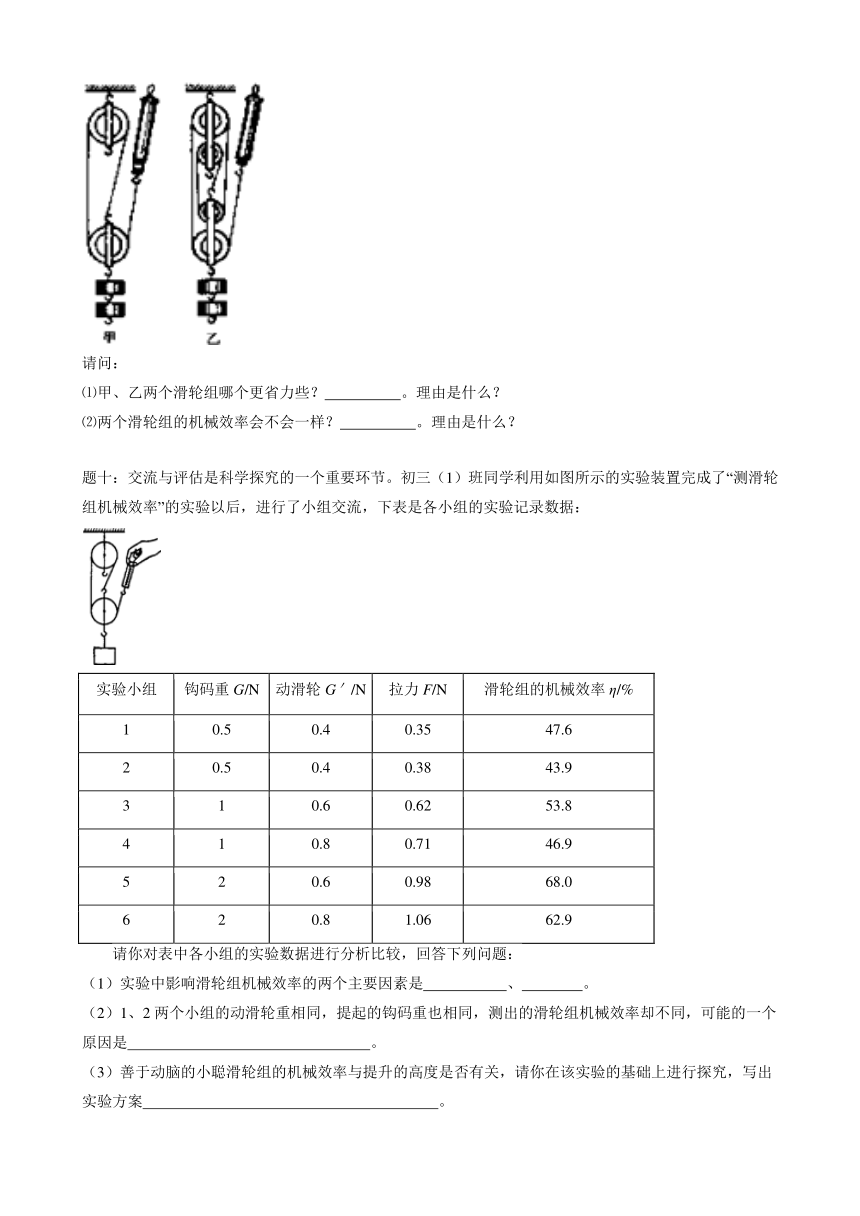
我们要通过实验测出图中甲和乙两个滑轮组的机械效率。
请问:
⑴甲、乙两个滑轮组哪个更省力些? 。理由是什么?
⑵两个滑轮组的机械效率会不会一样? 。理由是什么?
交流与评估是科学探究的一个重要环节。初三(1)班同学利用如图所示的实验装置完成了“测滑轮组机械效率”的实验以后,进行了小组交流,下表是各小组的实验记录数据:
实验小组
钩码重G/N
动滑轮G'/N
拉力F/N
滑轮组的机械效率η/%
1
0.5
0.4
0.35
47.6
2
0.5
0.4
0.38
43.9
3
1
0.6
0.62
53.8
4
1
0.8
0.71
46.9
5
2
0.6
0.98
68.0
6
2
0.8
1.06
62.9
请你对表中各小组的实验数据进行分析比较,回答下列问题:
(1)实验中影响滑轮组机械效率的两个主要因素是 、 。
(2)1、2两个小组的动滑轮重相同,提起的钩码重也相同,测出的滑轮组机械效率却不同,可能的一个原因是 。
(3)善于动脑的小聪滑轮组的机械效率与提升的高度是否有关,请你在该实验的基础上进行探究,写出实验方案 。
机械效率(上)
课后练习参考答案
等于;800;80;减小
详解:使用动滑轮不计绳重和摩擦力时,物体的重力G和拉力F相等,所以当分别沿力F1和F2的方向匀速提起物体A时F1=F2;不计绳重和摩擦力时拉力F做的功为W总=W有=Gh=200N×4m=800J;拉力F的功率=;把这个滑轮改成动滑轮时,在提升重物同时克服动滑轮重力做功,使额外功增加,所以机械效率减小。
D
详解:物体上升的速度v = 0.1 m/s,n=3,则绳子自由端移动的速度为v′=3v=3×0.1 m/s =0.3 m/s;C项正确;人拉绳做功的功率P=Fv′=250N×0.3m/s=75W, A项正确;滑轮组的机械效率:η=,B项正确;F=(G物+G轮),即250 N=(600N+G动),G动=150 N,D项错误。
C
详解:甲图由2段绳子承担动滑轮和重物,则F甲=(G+G动),乙图由3段绳子承担动滑轮和重物,则F乙=(G+G动),可见乙图更省力;两滑轮组提升的重物相同,做的有用功相同,若不计绳重和摩擦,都需克服动滑轮重力做额外功,即做的额外功也相同,则两滑轮组的总功相同,根据可知两滑轮组的机械效率相同。本题应选C。
C
详解:甲滑轮组中有一个动滑轮,乙滑轮组中有两个动滑轮,所以若把物体提升相同的高度,乙滑轮组做的额外功多,所以A错误;若G1=G2,把物体提升相同的高度,则甲乙所做的有用功相同,总功=有用功+额外功,所以乙做的总功大于甲做的总功,所以B错误;若G1=G2,甲和乙的有用功相同,而乙做的额外功多,甲做的额外功少,所以甲的机械效率大于乙的机械效率,C选项正确;用同一个滑轮组提起不同的重物,所做的额外功不变,有用功发生变化,所以有用功在总功中的比值发生变化,所以机械效率发生变化,所以D错误。故选C。
(1)如图所示 (2)240 W (3)83.3%
详解:(1)如图所示,重物由六段绳子承担;
(2)铜钟上升60 cm,即0.6 m,一共有6段绳子,所以拉力作用的位移s=0.6×6=3.6m拉力做的功:W=Fs=4000N×3.6m=1.44×104J,
拉力的功率P=W/t=1.44×104J/60 s=240 W;
(3)W有=Gh=20000N×0.6m=1.2×104J,机械效率η=。
(1)如图所示 (2)66.7% (3)变大;物重;摩擦 (4)0.14
详解:本题综合考查测滑轮组的机械效率及滑轮组中力与距离的关系。由表中的s=3h可以推断出有三段绳子承担动滑轮和重物,根据“奇动偶定”的法则完成滑轮组的绕绳连线;由表中数据可以计算出第3次实验时滑轮组的机械效率为:
======66.7%;当提升重物增加时,拉绳的力将变大,绳与滑轮间的压力增大,则绳与滑轮间的摩擦力也将会变大,因此,除克服动滑轮重所做的额外功一定外,其它额外功也将变大,由此可知,在动滑轮和绳重一定的情况下,该滑轮组的机械效率与物重和摩擦均有关。第一次实验中,动力为0.7 N,钩码上升0.1m,重力的作用点移动距离0.3 m,功率P = 0.7 N×0.3 m/1.5 s=0.14 W。
B
详解:本题考查的是机械效率的计算。根据题意可以知道物体的重力没有做功,以地面为参照物,物体做匀速直线运动,根据二力平衡可以知道A处的拉力为45 N,机械效率。正确选项为B。
ABD
详解:分析图可知,拉力F做的功为总功,物体A克服摩擦做的功为有用功,该过程做的有用功功率为W有=fv,故A正确;动滑轮上绳子的段数为3段,拉力F移动的速度为物体移动速度的3倍为3v,所以拉力做功的功率为P=F×3v=3Fv,故B正确;机械效率为η=,故C错误;动滑轮上绳子的段数为3段,总功W总=F×3s=3Fs,拉力做的额外功W额=W总-W有=3Fs-fs=(3F-f)s,故D正确。故选ABD。
⑴乙;乙装置中吊起动滑轮绳子的股数多 ⑵不会;因为两装置所做的额外功不一样
详解:甲滑轮组由三段绳子承担物重,即提起物体用的力就是物重的三分之一;乙滑轮组由四段绳子承担重物,即提起重物用的力为物重的四分之一;因为乙装置中吊起动滑轮绳子的股数多,故乙更省力;甲乙两个滑轮组提起的物重相同,但动滑轮个数不同,所以所做额外功不相等,因此机械效率不同。
(1)钩码重;动滑轮重 (2)绳子自由端未沿竖直方向匀速移动 (3)用同一滑轮组提升同一重物,改变物体提升的高度并测出绳子自由端移动的距离,计算并比较归纳
详解:(1)分析表中实验数据,根据实验数据找出影响滑轮组效率的因素:由3、4或5、6可以看出,钩码重相同,动滑轮越重,机械效率越低;由3、5或4、6可以看出,动滑轮重相同,钩码越重,机械效率越高;由此可知,影响滑轮组机械效率的两个主要因素是:钩码重与动滑轮重;(2)探究滑轮组效率实验中,应沿竖直方向匀速拉动绳子自由端。由表中实验数据可知,1、2两个小组的动滑轮重相同,提起的钩码重也相同,拉力大小不同,这可能是由于没有沿竖直方向匀速拉动绳子自由端造成的,从而使测出的滑轮组机械效率不同;(3)探究滑轮组效率与提升高度的关系,应使用同一滑轮组,提升同一重物,改变物体提升的高度并测出绳子自由端移动的距离,计算并比较归纳。
如图所示,物体A所受重力为200 N,绳重和摩擦力不计,当分别沿力F1和F2的方向匀速提起物体A时,则F1 等于F2(选填“大于”、“小于”或“等于”),若10 s内A物体被匀速提升4 m,则拉力F1所做的功为 800J,功率为 80W,如果把这个滑轮改成动滑轮匀速竖直提升同样的重物,则机械效率将 减小(选填“增大”、“减小”或“不变”)。
如图所示,小丽用滑轮组匀速提升一个重为600 N的物体,物体上升的速度为0.1 m/s,人拉绳的力F为250 N,不计绳重和摩擦,下列说法不正确的是( )
A.人拉绳做功的功率为75 W B. 滑轮组的机械效率为80%
C.绳子自由端移动的速度为0.3 m/s D. 动滑轮重为100 N
某实验小组分别用如图所示的甲、乙两个滑轮组(每个滑轮重相同)匀速提起相同的重物。不计绳重及摩擦,下列说法正确的是( )
A.甲图省力,机械效率甲图大 B. 甲图省力,机械效率一样大
C.乙图省力,机械效率一样大 D. 乙图省力,机械效率乙图大
甲乙两个滑轮组如图所示,其中的每一个滑轮都相同,用它们分别将重物G1、G2提高相同的高度,不计滑轮组的摩擦,下列说法中正确的是( )
A.若G1=G2,拉力做的额外功相同
B.若G1=G2,拉力做的总功相同
C.若G1=G2,甲的机械效率大于乙的机械效率
D.用甲乙其中的任何一个滑轮组提起不同的重物,机械效率不变
山东临淄管仲纪念馆内有一口铜钟,质量为2 t 。 2013年4月,一男子钻到钟下玩耍,其他游客转动铜钟导致悬挂钟的绳索被扭断,该男子被困于钟内。闻讯赶到的消防员们迅速组装好滑轮组、站在地面一起向下拉绳将铜钟吊起,该男子趁机从钟下爬出脱困。(g取10 N/kg)问:
(1)消防员们站在地面一起向下拉绳将铜钟吊起,请画出最省力的绳子绕法。
(2)消防员们在绳子自由端共施加4000 N的力,使铜钟在1 min内匀速缓慢上升60 cm,请计算绳子自由端拉力做功的功率。
(3)此过程中滑轮组的机械效率是多少?
下表是小明测一滑轮组机械效率时收集的有关数据。
动滑轮重
G动/N
物重
G/N
钩码上升
高度h/m
动力
F/N
动力作用点移
动距离s/m
滑轮组的
机械效率
1
0.5
1
0.1
0.7
0.3
47.6%
2
0.5
2
0.1
1.1
0.3
60.6%
3
0.5
4
0.1
2
0.3
(1)请在图中画出实验中滑轮组的绕绳方法。
(2)将表格中的数据补充完整。
(3)用同一滑轮组提升不同重物至同一高度,提升的物重增加时,除克服动滑轮重所做的额外功外,其它额外功将_________ (选填“变大”、“变小”或“不变”)。进一步分析可知,在动滑轮和绳重一定的情况下,该滑轮组的机械效率与_________和_________有关。
(4)第一次实验中,钩码上升0.1 m所用的时间为1.5 s ,则动力的功率为_________W。
如图所示,利用轻质滑轮组匀速拉动水平地面上重为300 N的物体,拉力F的大小为30 N。若物体和地面之间的摩擦力大小为45 N,则A处的拉力大小和滑轮组的机械效率分别为( )
A.45N、50% B.45 N、75% C.60 N、50% D.60 N、75%
(多选)如图所示,在水平拉力F的作用下,使物体A沿水平面以速度v向右匀速运动了距离s,若物重为G,平面对物体的摩擦力为f。下列说法正确的是( )
A.有用功的功率为fv B.拉力的功率为3Fv
C.装置的机械效率为 D.额外功为(3F-f)s
我们要通过实验测出图中甲和乙两个滑轮组的机械效率。
请问:
⑴甲、乙两个滑轮组哪个更省力些? 。理由是什么?
⑵两个滑轮组的机械效率会不会一样? 。理由是什么?
交流与评估是科学探究的一个重要环节。初三(1)班同学利用如图所示的实验装置完成了“测滑轮组机械效率”的实验以后,进行了小组交流,下表是各小组的实验记录数据:
实验小组
钩码重G/N
动滑轮G'/N
拉力F/N
滑轮组的机械效率η/%
1
0.5
0.4
0.35
47.6
2
0.5
0.4
0.38
43.9
3
1
0.6
0.62
53.8
4
1
0.8
0.71
46.9
5
2
0.6
0.98
68.0
6
2
0.8
1.06
62.9
请你对表中各小组的实验数据进行分析比较,回答下列问题:
(1)实验中影响滑轮组机械效率的两个主要因素是 、 。
(2)1、2两个小组的动滑轮重相同,提起的钩码重也相同,测出的滑轮组机械效率却不同,可能的一个原因是 。
(3)善于动脑的小聪滑轮组的机械效率与提升的高度是否有关,请你在该实验的基础上进行探究,写出实验方案 。
机械效率(上)
课后练习参考答案
等于;800;80;减小
详解:使用动滑轮不计绳重和摩擦力时,物体的重力G和拉力F相等,所以当分别沿力F1和F2的方向匀速提起物体A时F1=F2;不计绳重和摩擦力时拉力F做的功为W总=W有=Gh=200N×4m=800J;拉力F的功率=;把这个滑轮改成动滑轮时,在提升重物同时克服动滑轮重力做功,使额外功增加,所以机械效率减小。
D
详解:物体上升的速度v = 0.1 m/s,n=3,则绳子自由端移动的速度为v′=3v=3×0.1 m/s =0.3 m/s;C项正确;人拉绳做功的功率P=Fv′=250N×0.3m/s=75W, A项正确;滑轮组的机械效率:η=,B项正确;F=(G物+G轮),即250 N=(600N+G动),G动=150 N,D项错误。
C
详解:甲图由2段绳子承担动滑轮和重物,则F甲=(G+G动),乙图由3段绳子承担动滑轮和重物,则F乙=(G+G动),可见乙图更省力;两滑轮组提升的重物相同,做的有用功相同,若不计绳重和摩擦,都需克服动滑轮重力做额外功,即做的额外功也相同,则两滑轮组的总功相同,根据可知两滑轮组的机械效率相同。本题应选C。
C
详解:甲滑轮组中有一个动滑轮,乙滑轮组中有两个动滑轮,所以若把物体提升相同的高度,乙滑轮组做的额外功多,所以A错误;若G1=G2,把物体提升相同的高度,则甲乙所做的有用功相同,总功=有用功+额外功,所以乙做的总功大于甲做的总功,所以B错误;若G1=G2,甲和乙的有用功相同,而乙做的额外功多,甲做的额外功少,所以甲的机械效率大于乙的机械效率,C选项正确;用同一个滑轮组提起不同的重物,所做的额外功不变,有用功发生变化,所以有用功在总功中的比值发生变化,所以机械效率发生变化,所以D错误。故选C。
(1)如图所示 (2)240 W (3)83.3%
详解:(1)如图所示,重物由六段绳子承担;
(2)铜钟上升60 cm,即0.6 m,一共有6段绳子,所以拉力作用的位移s=0.6×6=3.6m拉力做的功:W=Fs=4000N×3.6m=1.44×104J,
拉力的功率P=W/t=1.44×104J/60 s=240 W;
(3)W有=Gh=20000N×0.6m=1.2×104J,机械效率η=。
(1)如图所示 (2)66.7% (3)变大;物重;摩擦 (4)0.14
详解:本题综合考查测滑轮组的机械效率及滑轮组中力与距离的关系。由表中的s=3h可以推断出有三段绳子承担动滑轮和重物,根据“奇动偶定”的法则完成滑轮组的绕绳连线;由表中数据可以计算出第3次实验时滑轮组的机械效率为:
======66.7%;当提升重物增加时,拉绳的力将变大,绳与滑轮间的压力增大,则绳与滑轮间的摩擦力也将会变大,因此,除克服动滑轮重所做的额外功一定外,其它额外功也将变大,由此可知,在动滑轮和绳重一定的情况下,该滑轮组的机械效率与物重和摩擦均有关。第一次实验中,动力为0.7 N,钩码上升0.1m,重力的作用点移动距离0.3 m,功率P = 0.7 N×0.3 m/1.5 s=0.14 W。
B
详解:本题考查的是机械效率的计算。根据题意可以知道物体的重力没有做功,以地面为参照物,物体做匀速直线运动,根据二力平衡可以知道A处的拉力为45 N,机械效率。正确选项为B。
ABD
详解:分析图可知,拉力F做的功为总功,物体A克服摩擦做的功为有用功,该过程做的有用功功率为W有=fv,故A正确;动滑轮上绳子的段数为3段,拉力F移动的速度为物体移动速度的3倍为3v,所以拉力做功的功率为P=F×3v=3Fv,故B正确;机械效率为η=,故C错误;动滑轮上绳子的段数为3段,总功W总=F×3s=3Fs,拉力做的额外功W额=W总-W有=3Fs-fs=(3F-f)s,故D正确。故选ABD。
⑴乙;乙装置中吊起动滑轮绳子的股数多 ⑵不会;因为两装置所做的额外功不一样
详解:甲滑轮组由三段绳子承担物重,即提起物体用的力就是物重的三分之一;乙滑轮组由四段绳子承担重物,即提起重物用的力为物重的四分之一;因为乙装置中吊起动滑轮绳子的股数多,故乙更省力;甲乙两个滑轮组提起的物重相同,但动滑轮个数不同,所以所做额外功不相等,因此机械效率不同。
(1)钩码重;动滑轮重 (2)绳子自由端未沿竖直方向匀速移动 (3)用同一滑轮组提升同一重物,改变物体提升的高度并测出绳子自由端移动的距离,计算并比较归纳
详解:(1)分析表中实验数据,根据实验数据找出影响滑轮组效率的因素:由3、4或5、6可以看出,钩码重相同,动滑轮越重,机械效率越低;由3、5或4、6可以看出,动滑轮重相同,钩码越重,机械效率越高;由此可知,影响滑轮组机械效率的两个主要因素是:钩码重与动滑轮重;(2)探究滑轮组效率实验中,应沿竖直方向匀速拉动绳子自由端。由表中实验数据可知,1、2两个小组的动滑轮重相同,提起的钩码重也相同,拉力大小不同,这可能是由于没有沿竖直方向匀速拉动绳子自由端造成的,从而使测出的滑轮组机械效率不同;(3)探究滑轮组效率与提升高度的关系,应使用同一滑轮组,提升同一重物,改变物体提升的高度并测出绳子自由端移动的距离,计算并比较归纳。
