数学人教A版(2019)选择性必修第一册第二章直线和圆的方程章末总结(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册第二章直线和圆的方程章末总结(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
章末总结
第 二 章 直线和圆的方程
人教A版2019选修第一册
01知识结构
PART ONE
知识结构
倾斜角
斜率
范围:__________
定义:当直线l与x轴相交时,我们取x轴作为基准,x轴_________与直线
l__________之间所成角,叫做直线的倾斜角.
定义:倾斜角α(α≠90°)的___________叫做这条直线的斜率,即 k=_____.
斜率公式:过两点P1(x1,y1), P2(x2,y2)(x1≠x2)的直线的斜率公式为
______________.
正方向
向上方向
正切值
tanα
[0°,180°)
1.直线切斜角与斜率
知识结构
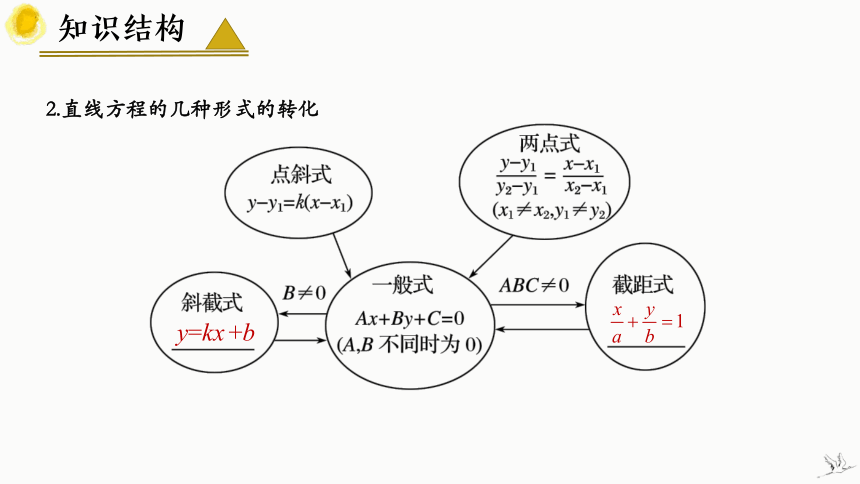
2.直线方程的几种形式的转化
y=kx +b
知识结构
设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则
(1)平行 A1B2-A2B1=0且B1C2-B2C1≠0;
(2)相交 A1B2-A2B1≠0;
3.两条直线的位置关系
(4)垂直 A1A2+B1B2=0;
知识结构
4.距离公式
(1)两点间的距离公式
已知点P1(x1,y1),P2(x2,y2),
则|P1P2|= .
(2)点到直线的距离公式
①点P(x0,y0)到直线l:Ax+By+C=0的距离d= ;
②两平行直线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离d= .
知识结构
1.圆的方程
(1)圆的标准方程: .
(2)圆的一般方程: .
2.点和圆的位置关系
设点P(x0,y0)及圆的方程(x-a)2+(y-b)2=r2.
(1)(x0-a)2+(y0-b)2>r2 点P .
(2)(x0-a)2+(y0-b)2(3)(x0-a)2+(y0-b)2=r2 点P .
3.直线与圆的位置关系
设直线l与圆C的圆心之间的距离为d,圆的半径为r,则d r 相离;d___r 相切;d r 相交.
(x-a)2+(y-b)2=r2
x2+y2+Dx+Ey+F=0(D2+E2-4F>0)
在圆外
在圆内
在圆上
>
=
<
知识结构
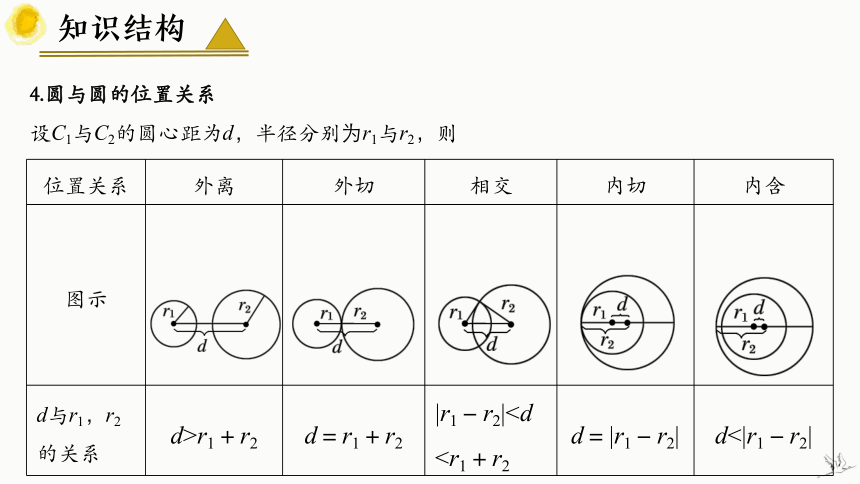
4.圆与圆的位置关系
设C1与C2的圆心距为d,半径分别为r1与r2,则
位置关系 外离 外切 相交 内切 内含
图示
d与r1,r2的关系 d>r1+r2 d=r1+r2 |r1-r2|知识结构
5.与圆有关的最值问题的常见类型
(1)形如μ= 形式的最值问题,可转化为动直线斜率的最值问题.
(2)形如t=ax+by形式的最值问题,可转化为动直线截距的最值问题.
(3)形如(x-a)2+(y-b)2形式的最值问题,可转化为动点到定点距离的平方的最值问题.
6.计算直线被圆截得的弦长的常用方法
(1)几何方法
运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算.
(2)代数方法
运用根与系数的关系及弦长公式
注:圆的弦长、弦心距的计算常用几何方法.
02直线和圆的方程的应用
PART ONE
知识应用
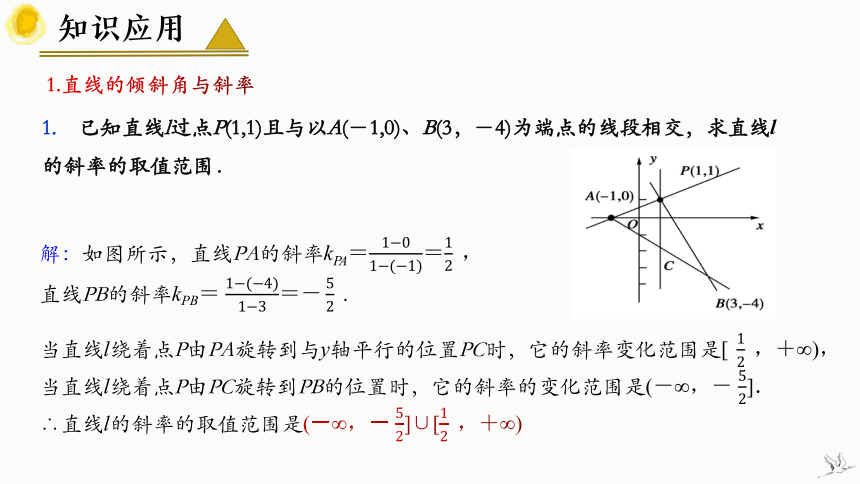
1.直线的倾斜角与斜率
1. 已知直线l过点P(1,1)且与以A(-1,0)、B(3,-4)为端点的线段相交,求直线l的斜率的取值范围.
解:如图所示,直线PA的斜率kPA==,
直线PB的斜率kPB= =.
当直线l绕着点P由PA旋转到与y轴平行的位置PC时,它的斜率变化范围是[,+∞),
当直线l绕着点P由PC旋转到PB的位置时,它的斜率的变化范围是(-∞,- ].
∴直线l的斜率的取值范围是(-∞,- ]∪[,+∞)
知识应用
1. 过点A(-5,-4)作一直线l,使它与两坐标轴相交且与两轴所围成的三角形的面积为5,求直线l的方程.
2.求直线的方程
解:由题意的,直线l的斜率存在。
设直线为y+4=k(x+5),与x轴交点为(5,0),与y轴交点(0,5k4)
得25k2-30k+16=0或25k2-50k+16=0,
解得k=,或k=,
所以所求直线l的方程为2x-5y-10=0,或8x-5y+20=0.
知识应用
2.求通过两条直线x+3y-10=0和3x-y=0的交点,且距原点为1的直线方程.
解: 法一:过两条直线交点的直线系方程为x+3y-10+λ(3x-y)=0,
即(1+3λ)x+(3-λ)y-10=0.①
∵原点到直线的距离为1,即=1,解得λ2=9,
∴λ=±3.代入方程①中,
得所求直线方程为x=1或4x-3y+5=0.
知识应用
法二:由方程组 解得两条直线的交点为A(1,3).
①当斜率存在时,设所求直线方程为y-3=k(x-1),即kx-y+3-k=0.
∵原点到直线的距离为1,即 =1,∴|3-k|=,∴k= .
∴直线方程为y-3=(x-1),即4x-3y+5=0.
②当直线斜率不存在时,直线方程为x=1也符合题意.
故所求直线方程为x=1或4x-3y+5=0.
2.求通过两条直线x+3y-10=0和3x-y=0的交点,且距原点为1的直线方程.
知识应用
常见的直线系有:
(1)过已知点P(x0,y0)的直线系y-y0=k(x-x0)(k为参数).
(2)斜率为k的平行直线系方程y=kx+b(b为参数).
(3)与已知直线Ax+By+C=0平行的直线系方程为Ax+By+λ=0(λ为参数,λ≠C).
(4)与已知直线Ax+By+C=0垂直的直线系方程为Bx-Ay+λ=0(λ为参数).
(5)过直线:A1x+B1y+C1=0与:A2x+B2y+C2=0的交点的直线系方程:A1x+B1y+C1+λ(A2x+B2y+C2)=0(λ为参数)(但不包含直线A2x+B2y+C2=0).
知识应用
3.两条直线的位置关系
1.已知两条直线l1:ax-by+4=0和l2:(a-1)x+y+b=0,分别求满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与直线l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
分析 对于(1),由题意列出关于a,b的方程组求解;
对于(2),先得出关于a,b的关系,再由原点到l1,l2的距离相等求解.
知识应用
解:(1)∵l1⊥l2,∴a(a-1)+(-b)=0,即a2-a-b=0. ①
又点(-3,-1)在l1上,∴-3a+b+4=0. ②
由①②解得a=2,b=2.
(2)∵l1∥l2且l2的斜率为1-a,∴l1的斜率也存在,=1-a,b=,
故l1与l2的方程分别为l1:(a-1)x+y+=0,l2:(a-1)x+y+ =0.
∵坐标原点到l1,l2的距离相等,
∴4| |=| |,a=2或a=. 因此或
知识应用
4.对称问题
1. 已知直线l:2x-3y+1=0,点A(-1,-2).求:
(1)点A关于直线l的对称点A′的坐标;
(2)直线m:3x-2y-6=0关于直线l的对称直线m′的方程;
(3)直线l关于点A的对称直线l′的方程.
知识应用
知识应用
易知M′(-3,-5),N′(-6,-7), 由两点式可得l′的方程为2x-3y-9=0.
法二:设直线l关于点A的对称直线l′上的任意一点P(x,y),则点P(x,y)关于点A(-1,-2)的对称点P′(-2-x,-4-y),
∵点P′在直线l上,
∴2(-2-x)-3(-4-y)+1=0,即2x-3y-9=0.
知识应用
5.数形结合
1.求函数y=+的最小值.
解: y= +
= +,
∴y表示x轴上的点P(x,0)到A(1,1),B(3,2)两点的距离之和.
如图,点B关于x轴的对称点B′(3,-2),∴|BP|=|BP|.
又∵两点之间线段最短,
∴y的最小值为|AB′|==.
知识应用
2.点P(-2,-1)到直线l:(1+3λ)x+(1+λ)y-2-5λ=0的距离为d,求d的最大值.
知识应用
6.求圆的方程
1.已知圆M经过直线l:2x+y+4=0及圆C:x2+y2+2x-4y+1=0的交点,且圆M的圆心到直线g:2x+6y-5=0的距离为3,求圆M的方程.
解:设经过直线l和圆C交点的圆系方程为x2+y2+2x-4y+1+λ(2x+y+4)=0,
则x2+y2+2(λ+1)x+(λ-4)y+4λ+1=0,
∴圆M的圆心M(-λ-1,),
∴=3,
解得λ=-11,或λ=13.
∴所求圆M的方程为x2+y2-20x-15y-43=0,
或x2+y2+28x+9y+53=0.
知识应用
已知点P(0,5)及圆C:x2+y2+4x-12y+24=0.
(1)若直线l过点P,且被圆C截得的线段长为 求l的方程;
7.直线与圆的位置关系
(2)求过点P的圆C的弦的中点的轨迹方程.
知识应用
设D是线段AB的中点,则CD⊥AB,
在Rt△ACD中,可得|CD|=2.
设所求直线l的斜率为k,则直线l的方程为y-5=kx,即kx-y+5=0.
此时直线l的方程为3x-4y+20=0.
又∵当直线l的斜率不存在时,也满足题意,此时方程为x=0,
∴所求直线l的方程为x=0或3x-4y+20=0.
知识应用
(2)设过点P的圆C的弦的中点为E(x,y),
则CE⊥PE,所以kCE·kPE=-1,
化简得所求轨迹方程为x2+y2+2x-11y+30=0.
知识应用
已知一个圆的圆心坐标为A(2,1),且与圆x2+y2-3x=0相交于P1,P2两点,若点A到直线P1P2的距离为 求这个圆的方程.
解 设圆的方程为(x-2)2+(y-1)2=r2,
即x2+y2-4x-2y+5-r2=0,
所以直线P1P2的方程为x+2y-5+r2=0.
解得r2=6.
故所求圆的方程是(x-2)2+(y-1)2=6.
8.圆与圆的位置关系
知识应用
4.最值与范围问题
已知实数x,y满足y=,则代数式 的取值范围为________.
解析:如图所示y=化为x2+y2=3(y≥0),表示的图形为半圆弧,
的几何意义为定点A(-3,-1)与半圆弧上任意一点M(x,y)的连线的斜率.
利用数形结合法可知kAB≤≤kAC.又B( ,0),kAB==,
设直线AC的方程为y+1=k(x+3),即kx-y+3k-1=0.
∵直线AC与半圆相切,∴ =,即3k2-3k-1=0,解得k= 或 (舍去).
∴kAC= .∴ ≤ ≤ .
知识应用
设点P(x,y)在圆x2+(y-1)2=1上.
(1)求的最小值;
(2)求的最小值.
解:(1)式子的几何意义是圆x2+(y-1)2=1上的点与定点(2,0)之间的距离.因为圆心(0,1)与定点(2,0)的距离是,圆的半径是1,所以的最小值是-1.
知识应用
(2)式子的几何意义是圆x2+(y-1)2=1上的点P(x,y)与定点(-1,-2)连线的斜率.如图,当连线为切线l1时,斜率最小,设l1的斜率为k,则l1的方程为kx-y+k-2=0,由直线与圆相切,得,解得k=.故的最小值是.
章末总结
第 二 章 直线和圆的方程
人教A版2019选修第一册
01知识结构
PART ONE
知识结构
倾斜角
斜率
范围:__________
定义:当直线l与x轴相交时,我们取x轴作为基准,x轴_________与直线
l__________之间所成角,叫做直线的倾斜角.
定义:倾斜角α(α≠90°)的___________叫做这条直线的斜率,即 k=_____.
斜率公式:过两点P1(x1,y1), P2(x2,y2)(x1≠x2)的直线的斜率公式为
______________.
正方向
向上方向
正切值
tanα
[0°,180°)
1.直线切斜角与斜率
知识结构
2.直线方程的几种形式的转化
y=kx +b
知识结构
设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则
(1)平行 A1B2-A2B1=0且B1C2-B2C1≠0;
(2)相交 A1B2-A2B1≠0;
3.两条直线的位置关系
(4)垂直 A1A2+B1B2=0;
知识结构
4.距离公式
(1)两点间的距离公式
已知点P1(x1,y1),P2(x2,y2),
则|P1P2|= .
(2)点到直线的距离公式
①点P(x0,y0)到直线l:Ax+By+C=0的距离d= ;
②两平行直线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离d= .
知识结构
1.圆的方程
(1)圆的标准方程: .
(2)圆的一般方程: .
2.点和圆的位置关系
设点P(x0,y0)及圆的方程(x-a)2+(y-b)2=r2.
(1)(x0-a)2+(y0-b)2>r2 点P .
(2)(x0-a)2+(y0-b)2
3.直线与圆的位置关系
设直线l与圆C的圆心之间的距离为d,圆的半径为r,则d r 相离;d___r 相切;d r 相交.
(x-a)2+(y-b)2=r2
x2+y2+Dx+Ey+F=0(D2+E2-4F>0)
在圆外
在圆内
在圆上
>
=
<
知识结构
4.圆与圆的位置关系
设C1与C2的圆心距为d,半径分别为r1与r2,则
位置关系 外离 外切 相交 内切 内含
图示
d与r1,r2的关系 d>r1+r2 d=r1+r2 |r1-r2|
5.与圆有关的最值问题的常见类型
(1)形如μ= 形式的最值问题,可转化为动直线斜率的最值问题.
(2)形如t=ax+by形式的最值问题,可转化为动直线截距的最值问题.
(3)形如(x-a)2+(y-b)2形式的最值问题,可转化为动点到定点距离的平方的最值问题.
6.计算直线被圆截得的弦长的常用方法
(1)几何方法
运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算.
(2)代数方法
运用根与系数的关系及弦长公式
注:圆的弦长、弦心距的计算常用几何方法.
02直线和圆的方程的应用
PART ONE
知识应用
1.直线的倾斜角与斜率
1. 已知直线l过点P(1,1)且与以A(-1,0)、B(3,-4)为端点的线段相交,求直线l的斜率的取值范围.
解:如图所示,直线PA的斜率kPA==,
直线PB的斜率kPB= =.
当直线l绕着点P由PA旋转到与y轴平行的位置PC时,它的斜率变化范围是[,+∞),
当直线l绕着点P由PC旋转到PB的位置时,它的斜率的变化范围是(-∞,- ].
∴直线l的斜率的取值范围是(-∞,- ]∪[,+∞)
知识应用
1. 过点A(-5,-4)作一直线l,使它与两坐标轴相交且与两轴所围成的三角形的面积为5,求直线l的方程.
2.求直线的方程
解:由题意的,直线l的斜率存在。
设直线为y+4=k(x+5),与x轴交点为(5,0),与y轴交点(0,5k4)
得25k2-30k+16=0或25k2-50k+16=0,
解得k=,或k=,
所以所求直线l的方程为2x-5y-10=0,或8x-5y+20=0.
知识应用
2.求通过两条直线x+3y-10=0和3x-y=0的交点,且距原点为1的直线方程.
解: 法一:过两条直线交点的直线系方程为x+3y-10+λ(3x-y)=0,
即(1+3λ)x+(3-λ)y-10=0.①
∵原点到直线的距离为1,即=1,解得λ2=9,
∴λ=±3.代入方程①中,
得所求直线方程为x=1或4x-3y+5=0.
知识应用
法二:由方程组 解得两条直线的交点为A(1,3).
①当斜率存在时,设所求直线方程为y-3=k(x-1),即kx-y+3-k=0.
∵原点到直线的距离为1,即 =1,∴|3-k|=,∴k= .
∴直线方程为y-3=(x-1),即4x-3y+5=0.
②当直线斜率不存在时,直线方程为x=1也符合题意.
故所求直线方程为x=1或4x-3y+5=0.
2.求通过两条直线x+3y-10=0和3x-y=0的交点,且距原点为1的直线方程.
知识应用
常见的直线系有:
(1)过已知点P(x0,y0)的直线系y-y0=k(x-x0)(k为参数).
(2)斜率为k的平行直线系方程y=kx+b(b为参数).
(3)与已知直线Ax+By+C=0平行的直线系方程为Ax+By+λ=0(λ为参数,λ≠C).
(4)与已知直线Ax+By+C=0垂直的直线系方程为Bx-Ay+λ=0(λ为参数).
(5)过直线:A1x+B1y+C1=0与:A2x+B2y+C2=0的交点的直线系方程:A1x+B1y+C1+λ(A2x+B2y+C2)=0(λ为参数)(但不包含直线A2x+B2y+C2=0).
知识应用
3.两条直线的位置关系
1.已知两条直线l1:ax-by+4=0和l2:(a-1)x+y+b=0,分别求满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与直线l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
分析 对于(1),由题意列出关于a,b的方程组求解;
对于(2),先得出关于a,b的关系,再由原点到l1,l2的距离相等求解.
知识应用
解:(1)∵l1⊥l2,∴a(a-1)+(-b)=0,即a2-a-b=0. ①
又点(-3,-1)在l1上,∴-3a+b+4=0. ②
由①②解得a=2,b=2.
(2)∵l1∥l2且l2的斜率为1-a,∴l1的斜率也存在,=1-a,b=,
故l1与l2的方程分别为l1:(a-1)x+y+=0,l2:(a-1)x+y+ =0.
∵坐标原点到l1,l2的距离相等,
∴4| |=| |,a=2或a=. 因此或
知识应用
4.对称问题
1. 已知直线l:2x-3y+1=0,点A(-1,-2).求:
(1)点A关于直线l的对称点A′的坐标;
(2)直线m:3x-2y-6=0关于直线l的对称直线m′的方程;
(3)直线l关于点A的对称直线l′的方程.
知识应用
知识应用
易知M′(-3,-5),N′(-6,-7), 由两点式可得l′的方程为2x-3y-9=0.
法二:设直线l关于点A的对称直线l′上的任意一点P(x,y),则点P(x,y)关于点A(-1,-2)的对称点P′(-2-x,-4-y),
∵点P′在直线l上,
∴2(-2-x)-3(-4-y)+1=0,即2x-3y-9=0.
知识应用
5.数形结合
1.求函数y=+的最小值.
解: y= +
= +,
∴y表示x轴上的点P(x,0)到A(1,1),B(3,2)两点的距离之和.
如图,点B关于x轴的对称点B′(3,-2),∴|BP|=|BP|.
又∵两点之间线段最短,
∴y的最小值为|AB′|==.
知识应用
2.点P(-2,-1)到直线l:(1+3λ)x+(1+λ)y-2-5λ=0的距离为d,求d的最大值.
知识应用
6.求圆的方程
1.已知圆M经过直线l:2x+y+4=0及圆C:x2+y2+2x-4y+1=0的交点,且圆M的圆心到直线g:2x+6y-5=0的距离为3,求圆M的方程.
解:设经过直线l和圆C交点的圆系方程为x2+y2+2x-4y+1+λ(2x+y+4)=0,
则x2+y2+2(λ+1)x+(λ-4)y+4λ+1=0,
∴圆M的圆心M(-λ-1,),
∴=3,
解得λ=-11,或λ=13.
∴所求圆M的方程为x2+y2-20x-15y-43=0,
或x2+y2+28x+9y+53=0.
知识应用
已知点P(0,5)及圆C:x2+y2+4x-12y+24=0.
(1)若直线l过点P,且被圆C截得的线段长为 求l的方程;
7.直线与圆的位置关系
(2)求过点P的圆C的弦的中点的轨迹方程.
知识应用
设D是线段AB的中点,则CD⊥AB,
在Rt△ACD中,可得|CD|=2.
设所求直线l的斜率为k,则直线l的方程为y-5=kx,即kx-y+5=0.
此时直线l的方程为3x-4y+20=0.
又∵当直线l的斜率不存在时,也满足题意,此时方程为x=0,
∴所求直线l的方程为x=0或3x-4y+20=0.
知识应用
(2)设过点P的圆C的弦的中点为E(x,y),
则CE⊥PE,所以kCE·kPE=-1,
化简得所求轨迹方程为x2+y2+2x-11y+30=0.
知识应用
已知一个圆的圆心坐标为A(2,1),且与圆x2+y2-3x=0相交于P1,P2两点,若点A到直线P1P2的距离为 求这个圆的方程.
解 设圆的方程为(x-2)2+(y-1)2=r2,
即x2+y2-4x-2y+5-r2=0,
所以直线P1P2的方程为x+2y-5+r2=0.
解得r2=6.
故所求圆的方程是(x-2)2+(y-1)2=6.
8.圆与圆的位置关系
知识应用
4.最值与范围问题
已知实数x,y满足y=,则代数式 的取值范围为________.
解析:如图所示y=化为x2+y2=3(y≥0),表示的图形为半圆弧,
的几何意义为定点A(-3,-1)与半圆弧上任意一点M(x,y)的连线的斜率.
利用数形结合法可知kAB≤≤kAC.又B( ,0),kAB==,
设直线AC的方程为y+1=k(x+3),即kx-y+3k-1=0.
∵直线AC与半圆相切,∴ =,即3k2-3k-1=0,解得k= 或 (舍去).
∴kAC= .∴ ≤ ≤ .
知识应用
设点P(x,y)在圆x2+(y-1)2=1上.
(1)求的最小值;
(2)求的最小值.
解:(1)式子的几何意义是圆x2+(y-1)2=1上的点与定点(2,0)之间的距离.因为圆心(0,1)与定点(2,0)的距离是,圆的半径是1,所以的最小值是-1.
知识应用
(2)式子的几何意义是圆x2+(y-1)2=1上的点P(x,y)与定点(-1,-2)连线的斜率.如图,当连线为切线l1时,斜率最小,设l1的斜率为k,则l1的方程为kx-y+k-2=0,由直线与圆相切,得,解得k=.故的最小值是.
