杠杆课后练习
图片预览

文档简介
杠杆课后练习
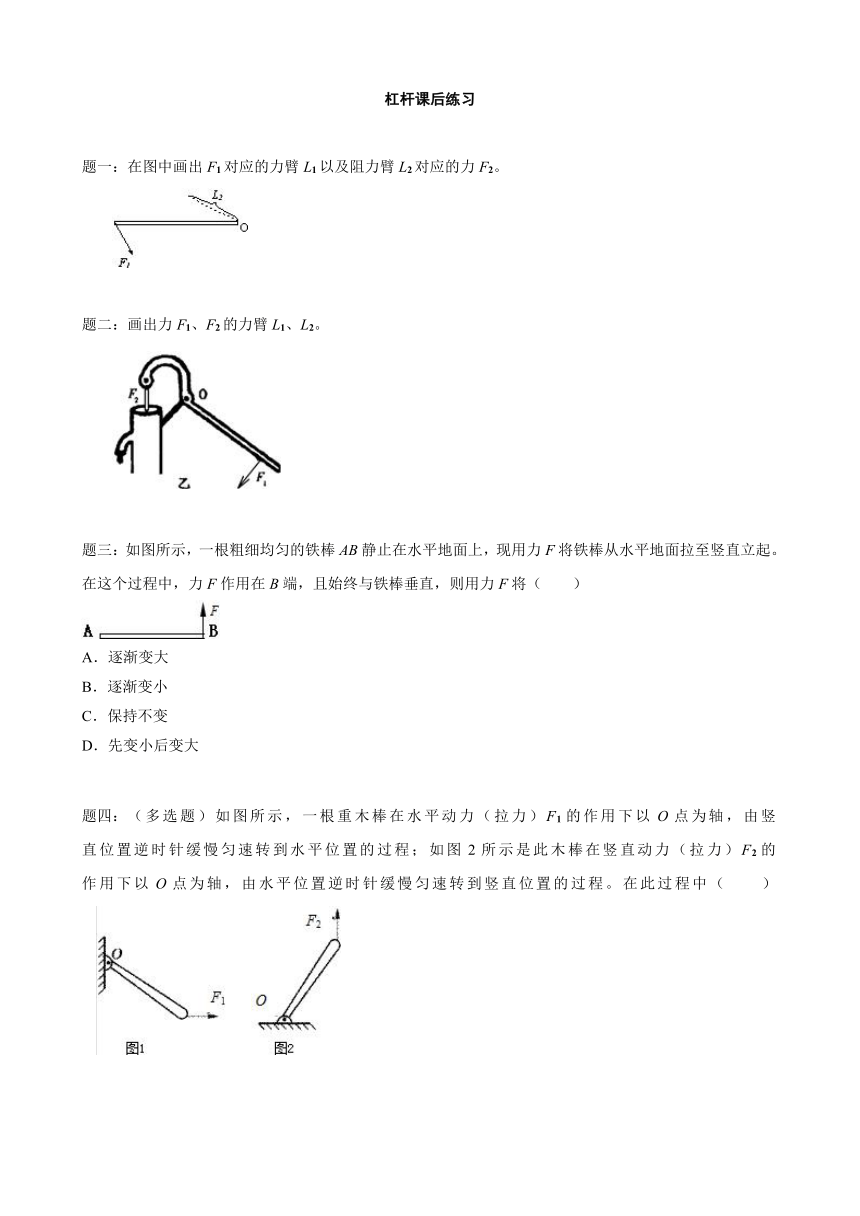
题一:在图中画出F1对应的力臂L1以及阻力臂L2对应的力F2。
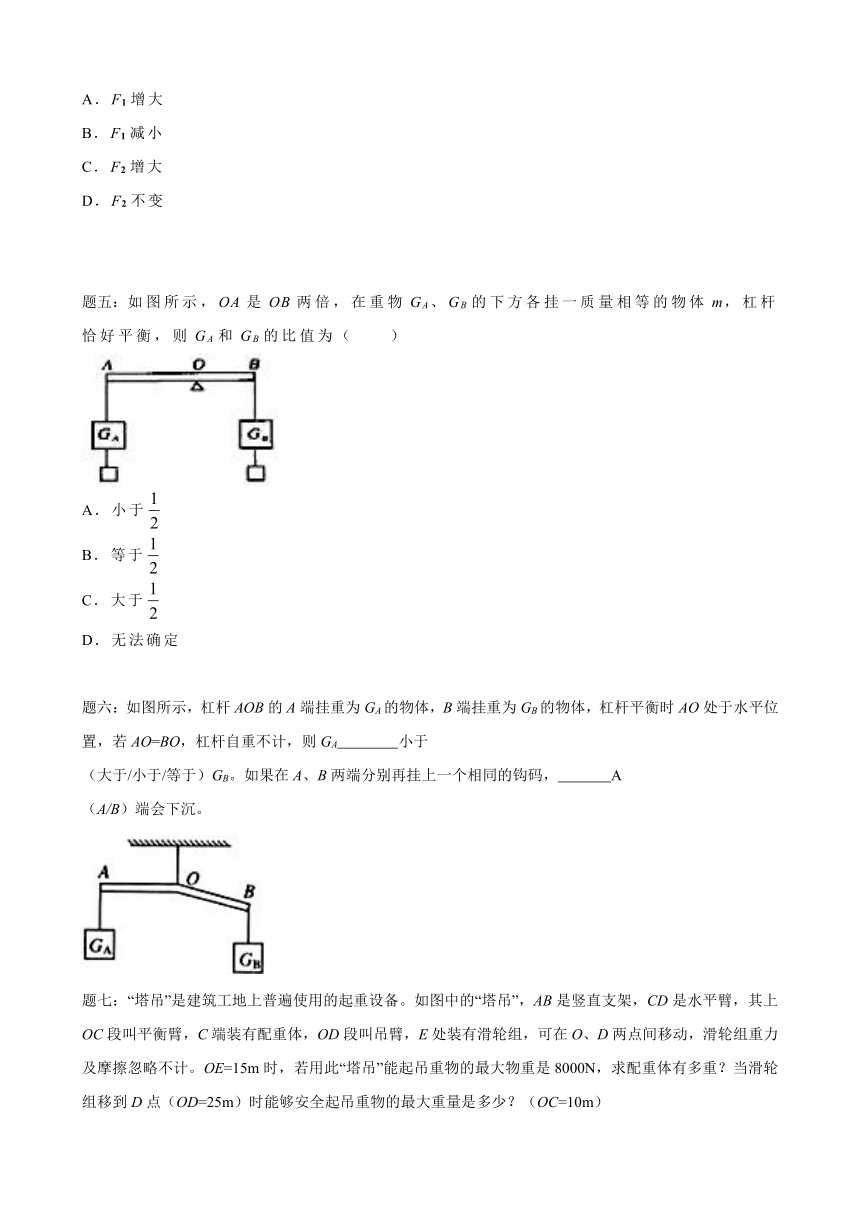
题二:画出力F1、F2的力臂L1、L2。
题三:如图所示,一根粗细均匀的铁棒AB静止在水平地面上,现用力F将铁棒从水平地面拉至竖直立起。在这个过程中,力F作用在B端,且始终与铁棒垂直,则用力F将( )
A.逐渐变大
B.逐渐变小
C.保持不变
D.先变小后变大
题四:(多选题)如图所示,一根重木棒在水平动力(拉力)F1的作用下以O点为轴,由竖直位置逆时针缓慢匀速转到水平位置的过程;如图2所示是此木棒在竖直动力(拉力)F2的作用下以O点为轴,由水平位置逆时针缓慢匀速转到竖直位置的过程。在此过程中( )
A.F1增大
B.F1减小
C.F2增大
D.F2不变
题五:如图所示,OA是OB两倍,在重物GA、GB的下方各挂一质量相等的物体m,杠杆恰好平衡,则GA和GB的比值为( )
A.小于
B.等于
C.大于
D.无法确定
题六:如图所示,杠杆AOB的A端挂重为GA的物体,B端挂重为GB的物体,杠杆平衡时AO处于水平位置,若AO=BO,杠杆自重不计,则GA 小于
(大于/小于/等于)GB。如果在A、B两端分别再挂上一个相同的钩码, A
(A/B)端会下沉。
题七:“塔吊”是建筑工地上普遍使用的起重设备。如图中的“塔吊”,AB是竖直支架,CD是水平臂,其上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E处装有滑轮组,可在O、D两点间移动,滑轮组重力及摩擦忽略不计。OE=15m时,若用此“塔吊”能起吊重物的最大物重是8000N,求配重体有多重?当滑轮组移到D点(OD=25m)时能够安全起吊重物的最大重量是多少?(OC=10m)
题八:“塔吊”是建筑工地上普遍使用的一种起重设备,如图是“塔吊”的简化图。OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在O、D之间移动。已知OE=10m,OC=15m,(不计“水平臂”和滑轮重力)。求:
(1)由杠杆的平衡条件可知,起重机的起重量随起吊幅度而变化,起吊幅度越大,起重量 。越小
(2)若在C点用此塔吊能起吊重物的最大重量是1.5×104N,则配重体的重量应为多少N?
(3)当滑轮移到D点时能够安全起吊重物的最大重量是9000N,则吊臂OD的长度是多少?
题九:如图所示,一根轻质木杆,A端细线下所挂50N的重物静止在水平地面上。当在B端加竖直向下的作用力F=30N时,木杆恰能在水平位置处于平衡状态,此时细线竖直。已知OA=15cm,OB=5cm,则重物对水平地面的压力为( )
A.80N
B.60N
C.40N
D.20N
题十:如图所示,轻质水平木杆AB可以绕O点转动,在杆的B端用细线悬挂了盛满水的正方体容器,使该容器静止在水平桌面上,该容器的边长为10cm,质量为0.2kg,已知AO长度是OB长度的3倍,在A点用F=4N的力竖直向下拉木杆时,容器对水平桌面的压力为 0
N,水对容器底部的压力为 10
N,(不计容器的厚度,ρ水=1.0×103kg/m3,g取10N/kg)
题十一:如图为一根硬棒,棒上标出了A、B、C三点,把它作杠杆使用.那么,当以棒上的???? 点为支点、动力作用在????? 点、阻力作用在?????? 点时,最省力。
题十二:三个和尚挑水吃的故事相信大家耳熟能详,甲图中和尚们商量出新的挑水方案 :胖和尚一人挑两小桶,瘦和尚和小和尚两人合抬一大桶。若乙图中后面的水桶向下沉,为保持水平平衡,胖和尚可采取的措施是 将肩向后移或将后面的桶向前移
(写出一种合理方法即可);丙图中小和尚为减轻瘦和尚的负担,小和尚可采取的措施是 。将桶向后移
。。
杠杆
课后练习参考答案
详解:过力臂L2的左端,作垂直于力臂L2的阻力作用线F2,F2与杠杆的交点A即为阻力作用点,由于阻力F1斜向下,因此力F2的方向应斜向上;过支点O做力F1的垂线段,即为动力臂L1。见图。
详解:如图,从支点向F1做垂线,垂线段的长度为动力臂L1。从支点向阻力F2的作用线做垂线,垂线段的长度为阻力臂L2,如图所示。
B
详解:在抬起的过程中,阻力F2不变,F与铁棒始终垂直,所以动力臂L1不变,由于铁棒的位置的变化,导致了阻力F2的阻力臂L2在变小,根据杠杆的平衡条件可得:F1L1=F2L2可知,L1、F2都不变,L2变小,所以F也在变小。
AD
详解:(1)如图甲与乙所示,当重木棒从甲位置向乙位置移动时,阻力G(即重力)不变,阻力臂LG从OA到OA'变大;动力臂LF从OD到OD'变小,由杠杆平衡条件:动力×动力臂=阻力×阻力臂,得:
G×LG=F1×LF
∵G不变,LG变大,变小LF
∴动力F1变大,故A正确;
(2)动力F2总是竖直向上,如图丙所示
∵△OAC∽△OBD
∴,在木棒转动过程中,OC与OD不变,OA是阻力臂, OB是动力臂,即动力臂和阻力臂的比值为定值。∵阻力(木棒重)G不变,由杠杆平衡条件:F2×OB=G×OA,可知:动力F2保持不变,故C错、D正确。
A
详解:由题知:杠杆处于水平平衡状态,OA:OB=2:1,
由杠杆平衡条件:(GA+G)×OA=(GB+G)×OB得出:
GA×OA+G×OA=GB×OB+G×OB,
因为G×OA>G×OB,所以GA×OA<GB×OB,即<=。
小于;A
详解:(1)如图,做出GB的力臂OC,
根据杠杆平衡条件得,GB×OC=GA×OA,
∵在直角△OCB中,OC<OB,OB=OA,OC<OA,
∴GA<GB;
(2)原来杠杆杠杆平衡,GA×OA=GB×OC,现在在A、B两端分别再挂上一个相同的钩码:左侧=GA×OA+G×OA,右侧=GB×OC+G×OC,∵OC<OA,∴GA×OA+G×OA>GB×OC+G×OC,∴杠杆不再平衡,杠杆A端将下沉。
12000N; 4800N
详解:(1)∵G配LOC=G1LOE
∴
(2)∵G配LOC=G2LOD ∴
(1)越小;(2)2.25×104N;(3)25m
详解:(1)由杠杆的平衡条件F1L1=F2L2(动力×动力臂=阻力×阻力臂)可知,当动力与动力臂不变时,阻力与阻力臂成反比;即阻力臂越大,阻力越小;阻力臂越小,阻力越大.而本题中的动力与动力臂都不变,则起吊幅度越大,起吊重量越小;
(2)在C点用此塔吊能起重物时,
∵GE×OE=GC×OC,即:GE×10m=1.5×104N×15m,GE=2.25×104N;
(3)在D点用此塔吊能起重物的最大重量是9000N时,吊臂OD的长度
∵GE×OE=GD×OD,即:2.25×104N×10m=9000N×OD,可得:OD=25m。
C
详解:根据杠杆平衡的条件:F1L1=F2L2,有:F1×OA=F2×OB;即:F1×15cm=30N×5cm,所以F1=10N,则重物对地面的压力F=50N-10N=40N。
0;10
详解:根据杠杆的平衡条件:FA?OA=FB?OB,又OA=3OB,所以FB=3FA=3×4N=12N,
容器的边长a=10cm=0.1m,
由得,m水=ρ水V=1.0×103kg/m3×(0.1m)3=1kg,
所以水和容器的总重力为G=(m容+m水)g=(0.2kg+1kg)×10N/kg=12N,
所以容器对桌面的压力F=G-FB=12N-12N=0N,
因为是正方体容器,所以F压=G水=m水g=1kg×10N/kg=10N。
A;C;B
详解:由图可知,当以A点为杠杆的支点时,动力作用在C点,则此时杠杆最长的力臂是AC的长,也就是整条杠杆的长;同时,若阻力作用在B点,则AB是三点间最短的距离,可以得到最短的阻力臂,因此,当以棒上的A点为支点、动力作用在C点、阻力作用在B点时,杠杆最省力。
将肩向后移或将后面的桶向前移;将桶向后移
详解:①如图乙,胖和尚挑水时,防止水桶后倾,应减小右边的力与力臂的乘积或增大左边的力与力臂的乘积,所以,要减小胖和尚后端的力臂,或增大前端的力臂,要使肩膀向扁担的后端移动,或使后面的水桶向前移动,或前面的水桶向前移动;
②对图丙,如下图,以小和尚的肩膀为支点O,水桶为阻力,瘦和尚的肩膀施加的力是动力,OA是阻力臂,OB是动力臂,要使瘦和尚施加的力小一些,小和尚可采取的措施是:可以使水桶靠近支点O,将桶向后移,即向小和尚方向移动。
题一:在图中画出F1对应的力臂L1以及阻力臂L2对应的力F2。
题二:画出力F1、F2的力臂L1、L2。
题三:如图所示,一根粗细均匀的铁棒AB静止在水平地面上,现用力F将铁棒从水平地面拉至竖直立起。在这个过程中,力F作用在B端,且始终与铁棒垂直,则用力F将( )
A.逐渐变大
B.逐渐变小
C.保持不变
D.先变小后变大
题四:(多选题)如图所示,一根重木棒在水平动力(拉力)F1的作用下以O点为轴,由竖直位置逆时针缓慢匀速转到水平位置的过程;如图2所示是此木棒在竖直动力(拉力)F2的作用下以O点为轴,由水平位置逆时针缓慢匀速转到竖直位置的过程。在此过程中( )
A.F1增大
B.F1减小
C.F2增大
D.F2不变
题五:如图所示,OA是OB两倍,在重物GA、GB的下方各挂一质量相等的物体m,杠杆恰好平衡,则GA和GB的比值为( )
A.小于
B.等于
C.大于
D.无法确定
题六:如图所示,杠杆AOB的A端挂重为GA的物体,B端挂重为GB的物体,杠杆平衡时AO处于水平位置,若AO=BO,杠杆自重不计,则GA 小于
(大于/小于/等于)GB。如果在A、B两端分别再挂上一个相同的钩码, A
(A/B)端会下沉。
题七:“塔吊”是建筑工地上普遍使用的起重设备。如图中的“塔吊”,AB是竖直支架,CD是水平臂,其上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E处装有滑轮组,可在O、D两点间移动,滑轮组重力及摩擦忽略不计。OE=15m时,若用此“塔吊”能起吊重物的最大物重是8000N,求配重体有多重?当滑轮组移到D点(OD=25m)时能够安全起吊重物的最大重量是多少?(OC=10m)
题八:“塔吊”是建筑工地上普遍使用的一种起重设备,如图是“塔吊”的简化图。OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在O、D之间移动。已知OE=10m,OC=15m,(不计“水平臂”和滑轮重力)。求:
(1)由杠杆的平衡条件可知,起重机的起重量随起吊幅度而变化,起吊幅度越大,起重量 。越小
(2)若在C点用此塔吊能起吊重物的最大重量是1.5×104N,则配重体的重量应为多少N?
(3)当滑轮移到D点时能够安全起吊重物的最大重量是9000N,则吊臂OD的长度是多少?
题九:如图所示,一根轻质木杆,A端细线下所挂50N的重物静止在水平地面上。当在B端加竖直向下的作用力F=30N时,木杆恰能在水平位置处于平衡状态,此时细线竖直。已知OA=15cm,OB=5cm,则重物对水平地面的压力为( )
A.80N
B.60N
C.40N
D.20N
题十:如图所示,轻质水平木杆AB可以绕O点转动,在杆的B端用细线悬挂了盛满水的正方体容器,使该容器静止在水平桌面上,该容器的边长为10cm,质量为0.2kg,已知AO长度是OB长度的3倍,在A点用F=4N的力竖直向下拉木杆时,容器对水平桌面的压力为 0
N,水对容器底部的压力为 10
N,(不计容器的厚度,ρ水=1.0×103kg/m3,g取10N/kg)
题十一:如图为一根硬棒,棒上标出了A、B、C三点,把它作杠杆使用.那么,当以棒上的???? 点为支点、动力作用在????? 点、阻力作用在?????? 点时,最省力。
题十二:三个和尚挑水吃的故事相信大家耳熟能详,甲图中和尚们商量出新的挑水方案 :胖和尚一人挑两小桶,瘦和尚和小和尚两人合抬一大桶。若乙图中后面的水桶向下沉,为保持水平平衡,胖和尚可采取的措施是 将肩向后移或将后面的桶向前移
(写出一种合理方法即可);丙图中小和尚为减轻瘦和尚的负担,小和尚可采取的措施是 。将桶向后移
。。
杠杆
课后练习参考答案
详解:过力臂L2的左端,作垂直于力臂L2的阻力作用线F2,F2与杠杆的交点A即为阻力作用点,由于阻力F1斜向下,因此力F2的方向应斜向上;过支点O做力F1的垂线段,即为动力臂L1。见图。
详解:如图,从支点向F1做垂线,垂线段的长度为动力臂L1。从支点向阻力F2的作用线做垂线,垂线段的长度为阻力臂L2,如图所示。
B
详解:在抬起的过程中,阻力F2不变,F与铁棒始终垂直,所以动力臂L1不变,由于铁棒的位置的变化,导致了阻力F2的阻力臂L2在变小,根据杠杆的平衡条件可得:F1L1=F2L2可知,L1、F2都不变,L2变小,所以F也在变小。
AD
详解:(1)如图甲与乙所示,当重木棒从甲位置向乙位置移动时,阻力G(即重力)不变,阻力臂LG从OA到OA'变大;动力臂LF从OD到OD'变小,由杠杆平衡条件:动力×动力臂=阻力×阻力臂,得:
G×LG=F1×LF
∵G不变,LG变大,变小LF
∴动力F1变大,故A正确;
(2)动力F2总是竖直向上,如图丙所示
∵△OAC∽△OBD
∴,在木棒转动过程中,OC与OD不变,OA是阻力臂, OB是动力臂,即动力臂和阻力臂的比值为定值。∵阻力(木棒重)G不变,由杠杆平衡条件:F2×OB=G×OA,可知:动力F2保持不变,故C错、D正确。
A
详解:由题知:杠杆处于水平平衡状态,OA:OB=2:1,
由杠杆平衡条件:(GA+G)×OA=(GB+G)×OB得出:
GA×OA+G×OA=GB×OB+G×OB,
因为G×OA>G×OB,所以GA×OA<GB×OB,即<=。
小于;A
详解:(1)如图,做出GB的力臂OC,
根据杠杆平衡条件得,GB×OC=GA×OA,
∵在直角△OCB中,OC<OB,OB=OA,OC<OA,
∴GA<GB;
(2)原来杠杆杠杆平衡,GA×OA=GB×OC,现在在A、B两端分别再挂上一个相同的钩码:左侧=GA×OA+G×OA,右侧=GB×OC+G×OC,∵OC<OA,∴GA×OA+G×OA>GB×OC+G×OC,∴杠杆不再平衡,杠杆A端将下沉。
12000N; 4800N
详解:(1)∵G配LOC=G1LOE
∴
(2)∵G配LOC=G2LOD ∴
(1)越小;(2)2.25×104N;(3)25m
详解:(1)由杠杆的平衡条件F1L1=F2L2(动力×动力臂=阻力×阻力臂)可知,当动力与动力臂不变时,阻力与阻力臂成反比;即阻力臂越大,阻力越小;阻力臂越小,阻力越大.而本题中的动力与动力臂都不变,则起吊幅度越大,起吊重量越小;
(2)在C点用此塔吊能起重物时,
∵GE×OE=GC×OC,即:GE×10m=1.5×104N×15m,GE=2.25×104N;
(3)在D点用此塔吊能起重物的最大重量是9000N时,吊臂OD的长度
∵GE×OE=GD×OD,即:2.25×104N×10m=9000N×OD,可得:OD=25m。
C
详解:根据杠杆平衡的条件:F1L1=F2L2,有:F1×OA=F2×OB;即:F1×15cm=30N×5cm,所以F1=10N,则重物对地面的压力F=50N-10N=40N。
0;10
详解:根据杠杆的平衡条件:FA?OA=FB?OB,又OA=3OB,所以FB=3FA=3×4N=12N,
容器的边长a=10cm=0.1m,
由得,m水=ρ水V=1.0×103kg/m3×(0.1m)3=1kg,
所以水和容器的总重力为G=(m容+m水)g=(0.2kg+1kg)×10N/kg=12N,
所以容器对桌面的压力F=G-FB=12N-12N=0N,
因为是正方体容器,所以F压=G水=m水g=1kg×10N/kg=10N。
A;C;B
详解:由图可知,当以A点为杠杆的支点时,动力作用在C点,则此时杠杆最长的力臂是AC的长,也就是整条杠杆的长;同时,若阻力作用在B点,则AB是三点间最短的距离,可以得到最短的阻力臂,因此,当以棒上的A点为支点、动力作用在C点、阻力作用在B点时,杠杆最省力。
将肩向后移或将后面的桶向前移;将桶向后移
详解:①如图乙,胖和尚挑水时,防止水桶后倾,应减小右边的力与力臂的乘积或增大左边的力与力臂的乘积,所以,要减小胖和尚后端的力臂,或增大前端的力臂,要使肩膀向扁担的后端移动,或使后面的水桶向前移动,或前面的水桶向前移动;
②对图丙,如下图,以小和尚的肩膀为支点O,水桶为阻力,瘦和尚的肩膀施加的力是动力,OA是阻力臂,OB是动力臂,要使瘦和尚施加的力小一些,小和尚可采取的措施是:可以使水桶靠近支点O,将桶向后移,即向小和尚方向移动。
