数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程(共26张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程(共26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 20:31:53 | ||
图片预览







文档简介
(共26张PPT)
圆锥曲线的方程
第三章
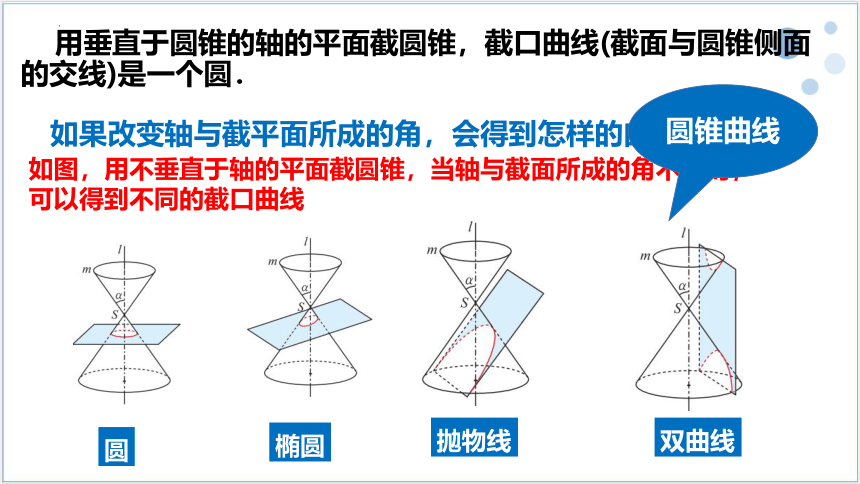
用垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.
如图,用不垂直于轴的平面截圆锥,当轴与截面所成的角不同时,可以得到不同的截口曲线
如果改变轴与截平面所成的角,会得到怎样的曲线呢
圆
椭圆
抛物线
双曲线
圆锥曲线
圆锥曲线与科技、生产以及人类生活有着紧密的关系。生活中很多例子都能说明圆锥曲线在生活中有着广泛的运用!
为什么会有这样广泛的运用?我们将可以从他们的几何特性及性质中得到答案!
本章继续采用坐标法研究圆锥曲线,回顾用坐标法研究直线、圆的过程,你能猜想研究的大概思路吗?
几何特征
方程
性质
应用
3.1.1椭圆及其标准方程
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类的生活中具有广泛的运用。那么,椭圆到底有怎样的几何特征?
新课导入
该如何利用这些特征建立椭圆的方程,进一步研究椭圆的几何性质?
实验探究
探究:取一条定长的细绳,把它的两端都固定在图板的同一点,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆.如果把细绳的两端拉开一段距离,分别固定在图板的两点,(如图),套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
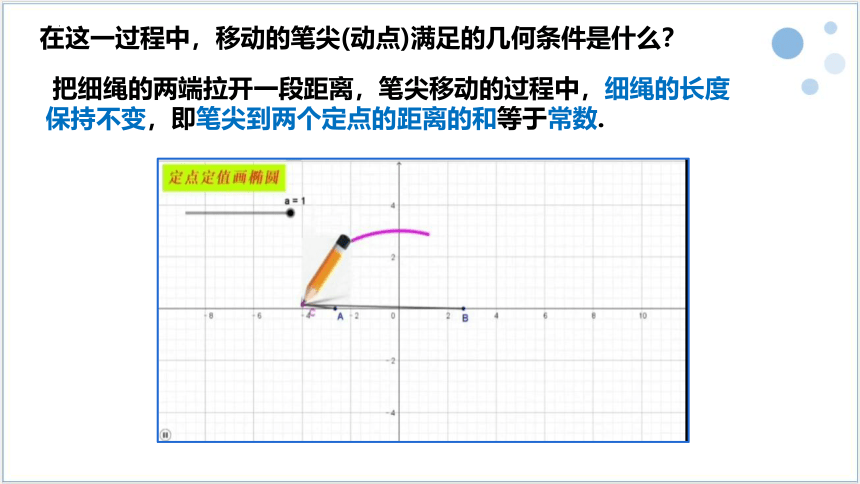
把细绳的两端拉开一段距离,笔尖移动的过程中,细绳的长度保持不变,即笔尖到两个定点的距离的和等于常数.
l
在这一过程中,移动的笔尖(动点)满足的几何条件是什么?
把平面内与两个定点的距离的和等于常数(大于)的点的轨迹叫做椭圆.
焦点
两焦点间的距离叫做椭圆的焦距(用表示)
焦距的一半称为半焦距(用表示).
问题1:你能用精确的数学语言来刻画椭圆吗?
F1
F2
M
追问1:椭圆定义中,需要特别关注哪些要素?
(1)两个定点:两点间距离确定;
(2)定长:轨迹上任意点到两定点距离和确定.
(3)
追问2:当动点到两定点、间距离之和等于两定点间的距离时,动点的轨迹是什么?(即)
线段AB
追问3:动点到两定点、间距离之和能小于两定点间的距离吗?(即)
点轨迹不存在
F1
F2
M
新知探究
思考:观察椭圆的形状,你认为怎样建立平面直角坐标系可能使所得的椭圆方程形式简单?
对称性
以经过椭圆两焦点,的直线为轴,线段的垂直平分线为轴,建立平面直角坐标系,如图所示
设是椭圆上任意一点,椭圆的焦距为,则焦点的坐标分别为.
根据椭圆的定义,设点与焦点的距离的和等于
所以+= .
下面怎么化简?
+= 将左边的一个根式移到右边,得= 两边平方得
=.
整理得. 两边平方得
.
整理得. 两边同除以,得.由椭圆的定义可知,,所以>0.
令=,
那么方程
.
思考:观察右图,你能从中找出表示 , , 的线段吗?
椭圆的标准方程
焦点在轴上
焦点坐标,
此时椭圆的标准方程是
焦点
思考:如图3.1-4,如果焦点在轴上,且的坐标分别为,的意义同上,那么椭圆的方程是什么?
推导过程请同学们课下独立完成
思考:椭圆的两种标准方程有什么异同?
焦点在轴上
焦点在轴上
共同点:
判断焦点位置:看,的分母大小,哪个分母大,焦点就在哪个坐标轴上
间的关系:,最大,大小不确定
焦点在坐标轴上,中心在坐标原点的椭圆
方程的左边是平方和,右边是1.
1.如果椭圆上一点P与焦点的距离等于6,那么点P与另一个焦点的距离是_________.
课堂练习
14
2.设是椭圆上的任意一点,若,是椭圆的两个焦点,则等于( ).
A.10 B.8 C.5 D.4
A
3.经过椭圆的右焦点作垂直于轴的直线AB,交椭圆于A,B两点,是椭圆的左焦点.
(1)求△AF1B的周长;
(2)如果AB不垂直于轴, △AF1B的周长有变化吗?为什么?
课堂练习
例题精讲
解:由于椭圆的焦点在轴上,设标准方程为.
例1.已知椭圆的两个焦点坐标分别是,,并且经过点,求它的标准方程.
由椭圆的定义知
所以
所以.
所求椭圆的标准方程为
定义法
例题精讲
例1.已知椭圆的两个焦点坐标分别是,,并且经过点,求它的标准方程.
待定系数法
课堂练习
例2 如图,在圆上任取一点P,过点作轴的垂线段,为垂足.当点P在圆上运动时,线段的中点的轨迹是什么?为什么?
解:设点的坐标为,点的坐标为,则点的坐标为.由点是线段的中点,得.
因为点在圆上,所以.①
把,代入方程①,得,即.
所以点的轨迹是椭圆.
例题精讲
由例2我们发现,可以由圆通过“压缩”得到椭圆.你能由圆通过“拉伸”得到椭圆吗?如何“拉伸”?由此你能发现椭圆与圆之间的关系吗?
将圆上的所有点的横坐标保持不变,纵坐标变为原来的时,利用伸缩变换的知识,可得到,即,此为椭圆方程.
同理将圆上所有点的横坐标保持不变,纵坐标变为原来的倍,利用伸缩变换可得,即,得到拉伸后的椭圆方程.所以椭圆可以由圆经过伸缩变换得到.
例题精讲
例3.如图,在,两点的坐标分别为,.直线相交于点,且它们的斜率之积是,求点的轨迹方程.
解:设点的坐标为,因为点的坐标为,
所以直线的斜率为
同理,直线的斜率为
由已知,有,
得点的轨迹方程为.
点的轨迹是除去两点的椭圆.
课堂小结
椭圆定义:
平面内到两个定点的距离之和等于常数(大于)的点的轨迹叫做椭圆
椭圆的标准方程:
焦点在轴上
焦点在轴上
圆锥曲线的方程
第三章
用垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.
如图,用不垂直于轴的平面截圆锥,当轴与截面所成的角不同时,可以得到不同的截口曲线
如果改变轴与截平面所成的角,会得到怎样的曲线呢
圆
椭圆
抛物线
双曲线
圆锥曲线
圆锥曲线与科技、生产以及人类生活有着紧密的关系。生活中很多例子都能说明圆锥曲线在生活中有着广泛的运用!
为什么会有这样广泛的运用?我们将可以从他们的几何特性及性质中得到答案!
本章继续采用坐标法研究圆锥曲线,回顾用坐标法研究直线、圆的过程,你能猜想研究的大概思路吗?
几何特征
方程
性质
应用
3.1.1椭圆及其标准方程
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类的生活中具有广泛的运用。那么,椭圆到底有怎样的几何特征?
新课导入
该如何利用这些特征建立椭圆的方程,进一步研究椭圆的几何性质?
实验探究
探究:取一条定长的细绳,把它的两端都固定在图板的同一点,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆.如果把细绳的两端拉开一段距离,分别固定在图板的两点,(如图),套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
把细绳的两端拉开一段距离,笔尖移动的过程中,细绳的长度保持不变,即笔尖到两个定点的距离的和等于常数.
l
在这一过程中,移动的笔尖(动点)满足的几何条件是什么?
把平面内与两个定点的距离的和等于常数(大于)的点的轨迹叫做椭圆.
焦点
两焦点间的距离叫做椭圆的焦距(用表示)
焦距的一半称为半焦距(用表示).
问题1:你能用精确的数学语言来刻画椭圆吗?
F1
F2
M
追问1:椭圆定义中,需要特别关注哪些要素?
(1)两个定点:两点间距离确定;
(2)定长:轨迹上任意点到两定点距离和确定.
(3)
追问2:当动点到两定点、间距离之和等于两定点间的距离时,动点的轨迹是什么?(即)
线段AB
追问3:动点到两定点、间距离之和能小于两定点间的距离吗?(即)
点轨迹不存在
F1
F2
M
新知探究
思考:观察椭圆的形状,你认为怎样建立平面直角坐标系可能使所得的椭圆方程形式简单?
对称性
以经过椭圆两焦点,的直线为轴,线段的垂直平分线为轴,建立平面直角坐标系,如图所示
设是椭圆上任意一点,椭圆的焦距为,则焦点的坐标分别为.
根据椭圆的定义,设点与焦点的距离的和等于
所以+= .
下面怎么化简?
+= 将左边的一个根式移到右边,得= 两边平方得
=.
整理得. 两边平方得
.
整理得. 两边同除以,得.由椭圆的定义可知,,所以>0.
令=,
那么方程
.
思考:观察右图,你能从中找出表示 , , 的线段吗?
椭圆的标准方程
焦点在轴上
焦点坐标,
此时椭圆的标准方程是
焦点
思考:如图3.1-4,如果焦点在轴上,且的坐标分别为,的意义同上,那么椭圆的方程是什么?
推导过程请同学们课下独立完成
思考:椭圆的两种标准方程有什么异同?
焦点在轴上
焦点在轴上
共同点:
判断焦点位置:看,的分母大小,哪个分母大,焦点就在哪个坐标轴上
间的关系:,最大,大小不确定
焦点在坐标轴上,中心在坐标原点的椭圆
方程的左边是平方和,右边是1.
1.如果椭圆上一点P与焦点的距离等于6,那么点P与另一个焦点的距离是_________.
课堂练习
14
2.设是椭圆上的任意一点,若,是椭圆的两个焦点,则等于( ).
A.10 B.8 C.5 D.4
A
3.经过椭圆的右焦点作垂直于轴的直线AB,交椭圆于A,B两点,是椭圆的左焦点.
(1)求△AF1B的周长;
(2)如果AB不垂直于轴, △AF1B的周长有变化吗?为什么?
课堂练习
例题精讲
解:由于椭圆的焦点在轴上,设标准方程为.
例1.已知椭圆的两个焦点坐标分别是,,并且经过点,求它的标准方程.
由椭圆的定义知
所以
所以.
所求椭圆的标准方程为
定义法
例题精讲
例1.已知椭圆的两个焦点坐标分别是,,并且经过点,求它的标准方程.
待定系数法
课堂练习
例2 如图,在圆上任取一点P,过点作轴的垂线段,为垂足.当点P在圆上运动时,线段的中点的轨迹是什么?为什么?
解:设点的坐标为,点的坐标为,则点的坐标为.由点是线段的中点,得.
因为点在圆上,所以.①
把,代入方程①,得,即.
所以点的轨迹是椭圆.
例题精讲
由例2我们发现,可以由圆通过“压缩”得到椭圆.你能由圆通过“拉伸”得到椭圆吗?如何“拉伸”?由此你能发现椭圆与圆之间的关系吗?
将圆上的所有点的横坐标保持不变,纵坐标变为原来的时,利用伸缩变换的知识,可得到,即,此为椭圆方程.
同理将圆上所有点的横坐标保持不变,纵坐标变为原来的倍,利用伸缩变换可得,即,得到拉伸后的椭圆方程.所以椭圆可以由圆经过伸缩变换得到.
例题精讲
例3.如图,在,两点的坐标分别为,.直线相交于点,且它们的斜率之积是,求点的轨迹方程.
解:设点的坐标为,因为点的坐标为,
所以直线的斜率为
同理,直线的斜率为
由已知,有,
得点的轨迹方程为.
点的轨迹是除去两点的椭圆.
课堂小结
椭圆定义:
平面内到两个定点的距离之和等于常数(大于)的点的轨迹叫做椭圆
椭圆的标准方程:
焦点在轴上
焦点在轴上
