江苏省南京市江宁区竹山中学2023-2024学年八年级上学期10月月考数学试题(无答案)
文档属性
| 名称 | 江苏省南京市江宁区竹山中学2023-2024学年八年级上学期10月月考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 498.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 23:31:46 | ||
图片预览

文档简介
八年级学情素养限时作业
数学(学科)
总分:100分 时间:100分钟
一、单选题(本题共16分,每小题2分)
1.交通警察要求司机开车时遵章行驶,在下列交通标志中,不是轴对称图形的是( )
A. B. C. D.
2.如图,平移后得到,,,则的度数是( )
A.55° B.45° C.80° D.100°
3.在中,、、的对边分别为a、b、c,下列条件不能判断是直角三角形的是( )
A. B.
C. D.
4.如图,中,BD平分,CD平分,过点D作直线平行于BC,分别交AB、AC于点E、F,若,,,则的周长为( )
A.13 B.12 C.15 D.20
5.如图,为等边三角形,要在外部取一点D,使得和全等,下面是两名同学做法:( )
甲:①作的角平分线l;②以B为圆心,BC长为半径画弧,交l于点D,点D即为所求;
乙:①过点B作平行于AC的直线l;②过点C作平行于AB的直线m,交l于点D,点D即为所求.
A.两人都正确 B.两人都错误 C.甲正确,乙错误 D.甲错误,乙正确
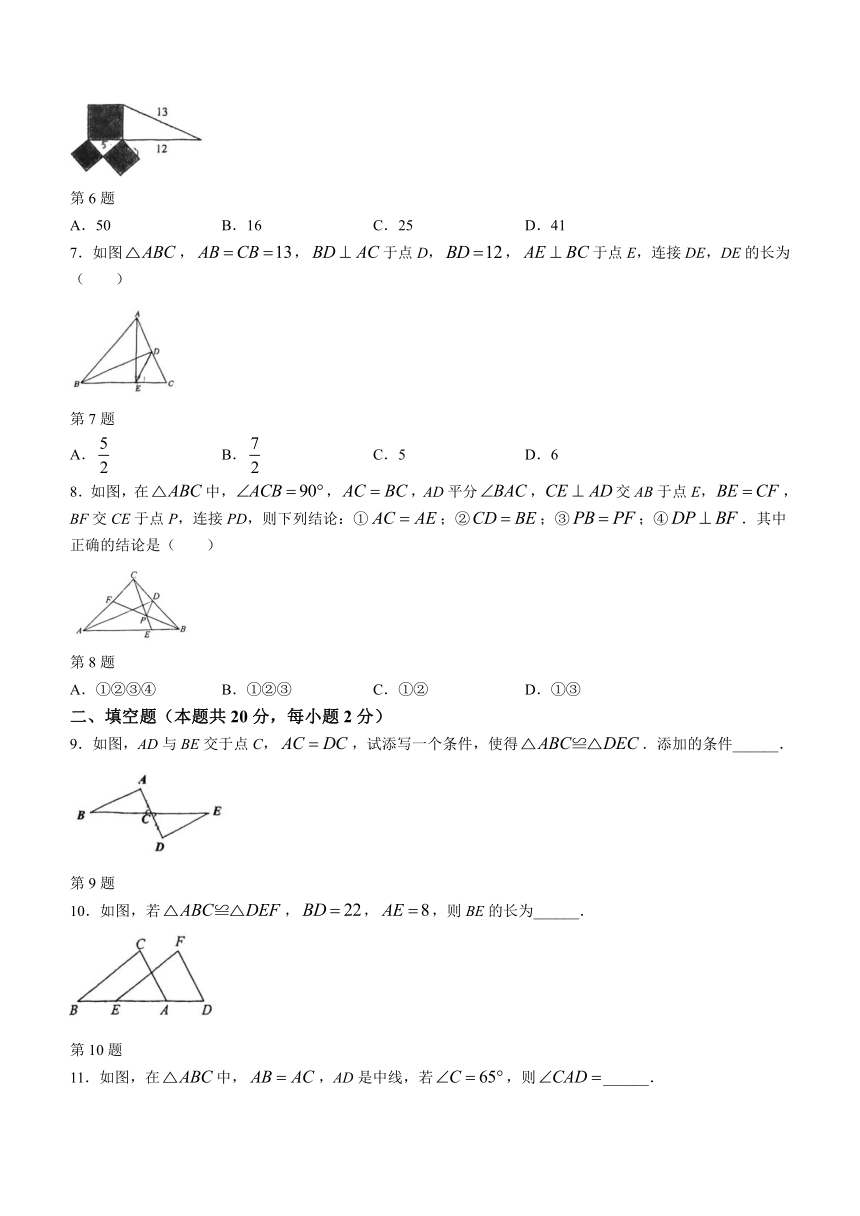
6.如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
第6题
A.50 B.16 C.25 D.41
7.如图,,于点D,,于点E,连接DE,DE的长为( )
第7题
A. B. C.5 D.6
8.如图,在中,,,AD平分,交AB于点E,,BF交CE于点P,连接PD,则下列结论:①;②;③;④.其中正确的结论是( )
第8题
A.①②③④ B.①②③ C.①② D.①③
二、填空题(本题共20分,每小题2分)
9.如图,AD与BE交于点C,,试添写一个条件,使得.添加的条件______.
第9题
10.如图,若,,,则BE的长为______.
第10题
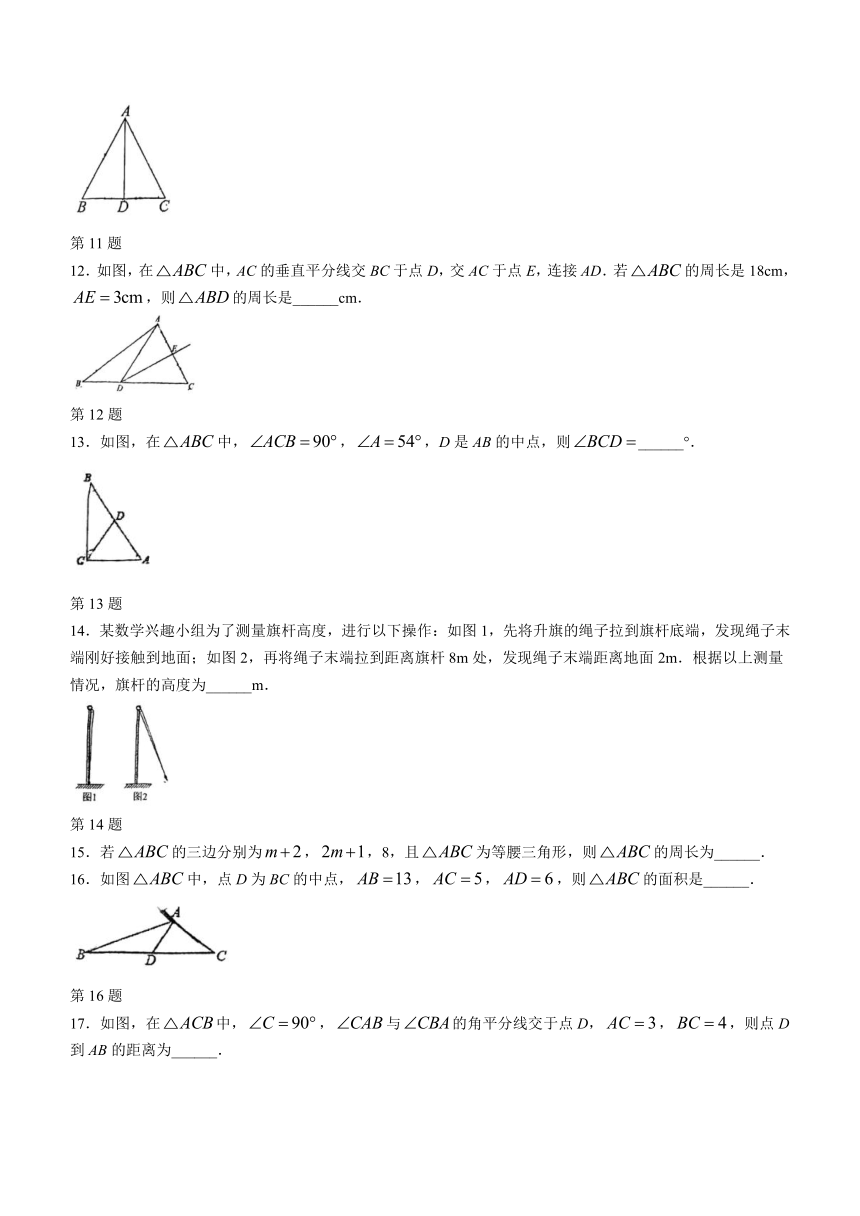
11.如图,在中,,AD是中线,若,则______.
第11题
12.如图,在中,AC的垂直平分线交BC于点D,交AC于点E,连接AD.若的周长是18cm,,则的周长是______cm.
第12题
13.如图,在中,,,D是AB的中点,则______°.
第13题
14.某数学兴趣小组为了测量旗杆高度,进行以下操作:如图1,先将升旗的绳子拉到旗杆底端,发现绳子末端刚好接触到地面;如图2,再将绳子末端拉到距离旗杆8m处,发现绳子末端距离地面2m.根据以上测量情况,旗杆的高度为______m.
第14题
15.若的三边分别为,,8,且为等腰三角形,则的周长为______.
16.如图中,点D为BC的中点,,,,则的面积是______.
第16题
17.如图,在中,,与的角平分线交于点D,,,则点D到AB的距离为______.
第17题
18.如图,在中,,,垂足为D,AF平分,交CD于点E,交CB于点F,若,,则CE的长为______.
第18题
三、解答题(本大题共64分)
19.(6分)如图,已知线段AD、BC相交于点O,,.求证:.
20.(8分)如图,四边形ABCD中,,,,且,求的度数.
21.(6分)如图是由边长为1的小正方形组成的网格,直线EF是一条网格线,点E,F在格点上,的三个顶点都在格点(网格线的交点)上.
(1)作出关于直线EF对称的;
(2)在直线EF上画出点M,使四边形AMBC的周长最小;
(3)在这个网格中,到点A和点B的距离相等的格点有______个.
22.(8分)证明:“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”
已知:如图,在中,______.
求证:______.
证明:
23.(6分)勾股定理是几何学中的明珠,充满着魅力,向常春1994年构造发现了一个新的证法,证法如下:把两个全等的直角三角形按如图1放置,,于点F,点E在边AB上,现设两直角边长分别为、,斜边长为,请用a、b、c分别表示出梯形ABCD、四边形AECD、的面积,再探究这三个图形面积之间的关系,可得到勾股定理
图1
(1)请根据上述图形的面积关系证明勾股定理;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,CD为两个村庄(看作直线上的两点),,,垂足分别为A、B,千米,千米,则两个村庄的距离为______千米.
图2
24.(8分)如图,在中,,,,将沿过B点的直线折叠,使点C落在AB边上的点D处,折痕与AC交于点E.
(1)试用尺规作图作出折痕BE;(要求:保留作图痕迹,不写作法.)
(2)连接DE,求线段DE的长度.
25.(10分)如图,长方形ABCD中,,,E为CD边上一点,.
(1)求AE的长;
(2)点P从点B出发,以每秒2个单位长度的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
①当t为何值时,是等腰三角形;
②当______时,.
26.(12分)
【问题探究】
(1)如图1,锐角中分别以AB、AC为边向外作等腰和等腰,使,,,连接BD,CE,试猜想BD与CE的大小关系,并证明理由.
【深入探究】
(2)如图2,四边形ABCD中,,,,求BD的长.
(3)如图3,在四边形ABCD中,连接AC,,,,,,求AD的长.
数学(学科)
总分:100分 时间:100分钟
一、单选题(本题共16分,每小题2分)
1.交通警察要求司机开车时遵章行驶,在下列交通标志中,不是轴对称图形的是( )
A. B. C. D.
2.如图,平移后得到,,,则的度数是( )
A.55° B.45° C.80° D.100°
3.在中,、、的对边分别为a、b、c,下列条件不能判断是直角三角形的是( )
A. B.
C. D.
4.如图,中,BD平分,CD平分,过点D作直线平行于BC,分别交AB、AC于点E、F,若,,,则的周长为( )
A.13 B.12 C.15 D.20
5.如图,为等边三角形,要在外部取一点D,使得和全等,下面是两名同学做法:( )
甲:①作的角平分线l;②以B为圆心,BC长为半径画弧,交l于点D,点D即为所求;
乙:①过点B作平行于AC的直线l;②过点C作平行于AB的直线m,交l于点D,点D即为所求.
A.两人都正确 B.两人都错误 C.甲正确,乙错误 D.甲错误,乙正确
6.如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
第6题
A.50 B.16 C.25 D.41
7.如图,,于点D,,于点E,连接DE,DE的长为( )
第7题
A. B. C.5 D.6
8.如图,在中,,,AD平分,交AB于点E,,BF交CE于点P,连接PD,则下列结论:①;②;③;④.其中正确的结论是( )
第8题
A.①②③④ B.①②③ C.①② D.①③
二、填空题(本题共20分,每小题2分)
9.如图,AD与BE交于点C,,试添写一个条件,使得.添加的条件______.
第9题
10.如图,若,,,则BE的长为______.
第10题
11.如图,在中,,AD是中线,若,则______.
第11题
12.如图,在中,AC的垂直平分线交BC于点D,交AC于点E,连接AD.若的周长是18cm,,则的周长是______cm.
第12题
13.如图,在中,,,D是AB的中点,则______°.
第13题
14.某数学兴趣小组为了测量旗杆高度,进行以下操作:如图1,先将升旗的绳子拉到旗杆底端,发现绳子末端刚好接触到地面;如图2,再将绳子末端拉到距离旗杆8m处,发现绳子末端距离地面2m.根据以上测量情况,旗杆的高度为______m.
第14题
15.若的三边分别为,,8,且为等腰三角形,则的周长为______.
16.如图中,点D为BC的中点,,,,则的面积是______.
第16题
17.如图,在中,,与的角平分线交于点D,,,则点D到AB的距离为______.
第17题
18.如图,在中,,,垂足为D,AF平分,交CD于点E,交CB于点F,若,,则CE的长为______.
第18题
三、解答题(本大题共64分)
19.(6分)如图,已知线段AD、BC相交于点O,,.求证:.
20.(8分)如图,四边形ABCD中,,,,且,求的度数.
21.(6分)如图是由边长为1的小正方形组成的网格,直线EF是一条网格线,点E,F在格点上,的三个顶点都在格点(网格线的交点)上.
(1)作出关于直线EF对称的;
(2)在直线EF上画出点M,使四边形AMBC的周长最小;
(3)在这个网格中,到点A和点B的距离相等的格点有______个.
22.(8分)证明:“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”
已知:如图,在中,______.
求证:______.
证明:
23.(6分)勾股定理是几何学中的明珠,充满着魅力,向常春1994年构造发现了一个新的证法,证法如下:把两个全等的直角三角形按如图1放置,,于点F,点E在边AB上,现设两直角边长分别为、,斜边长为,请用a、b、c分别表示出梯形ABCD、四边形AECD、的面积,再探究这三个图形面积之间的关系,可得到勾股定理
图1
(1)请根据上述图形的面积关系证明勾股定理;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,CD为两个村庄(看作直线上的两点),,,垂足分别为A、B,千米,千米,则两个村庄的距离为______千米.
图2
24.(8分)如图,在中,,,,将沿过B点的直线折叠,使点C落在AB边上的点D处,折痕与AC交于点E.
(1)试用尺规作图作出折痕BE;(要求:保留作图痕迹,不写作法.)
(2)连接DE,求线段DE的长度.
25.(10分)如图,长方形ABCD中,,,E为CD边上一点,.
(1)求AE的长;
(2)点P从点B出发,以每秒2个单位长度的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
①当t为何值时,是等腰三角形;
②当______时,.
26.(12分)
【问题探究】
(1)如图1,锐角中分别以AB、AC为边向外作等腰和等腰,使,,,连接BD,CE,试猜想BD与CE的大小关系,并证明理由.
【深入探究】
(2)如图2,四边形ABCD中,,,,求BD的长.
(3)如图3,在四边形ABCD中,连接AC,,,,,,求AD的长.
同课章节目录
