江苏省泰州市姜堰区第四中学2023-2024学年八年级上学期9月月考数学试题(无答案)
文档属性
| 名称 | 江苏省泰州市姜堰区第四中学2023-2024学年八年级上学期9月月考数学试题(无答案) | 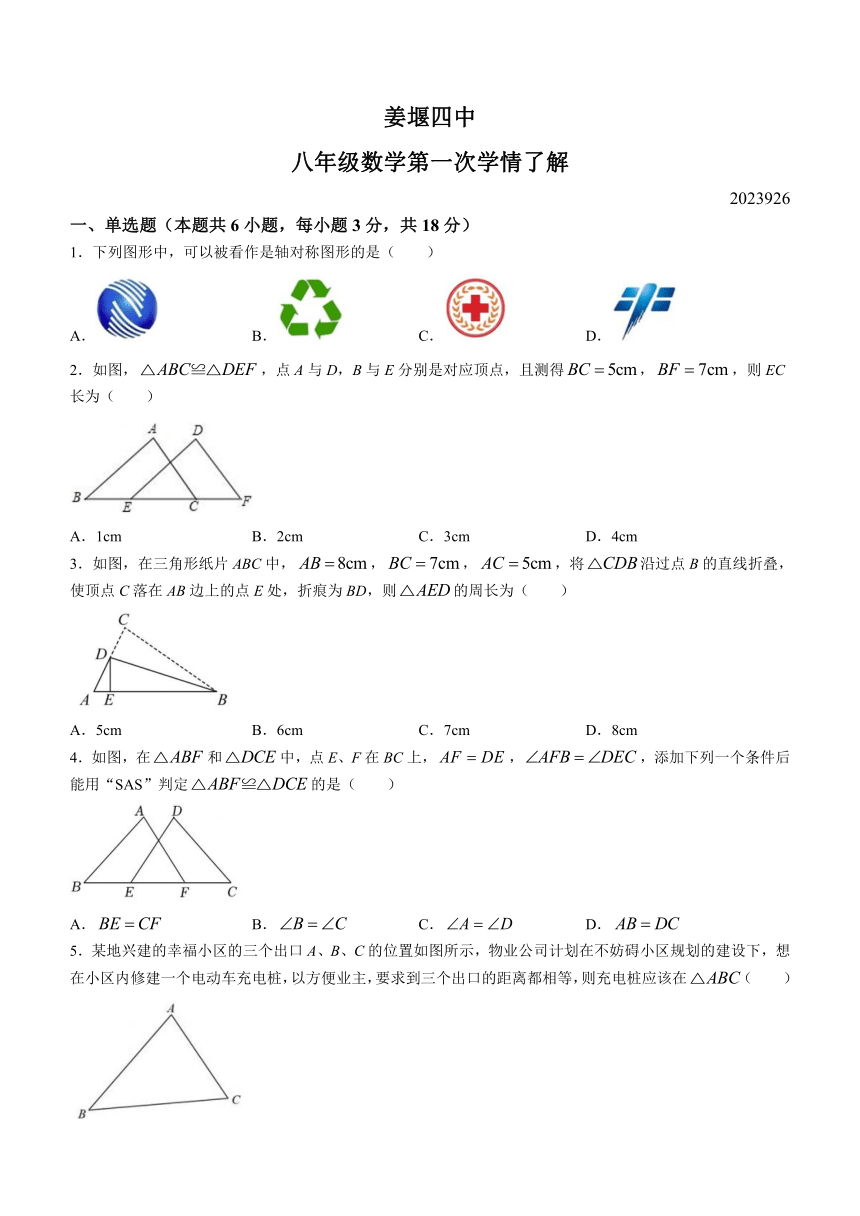 | |
| 格式 | docx | ||
| 文件大小 | 717.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 23:35:43 | ||
图片预览



文档简介
姜堰四中
八年级数学第一次学情了解
2023926
一、单选题(本题共6小题,每小题3分,共18分)
1.下列图形中,可以被看作是轴对称图形的是( )
A. B. C. D.
2.如图,,点A与D,B与E分别是对应顶点,且测得,,则EC长为( )
A.1cm B.2cm C.3cm D.4cm
3.如图,在三角形纸片ABC中,,,,将沿过点B的直线折叠,使顶点C落在AB边上的点E处,折痕为BD,则的周长为( )
A.5cm B.6cm C.7cm D.8cm
4.如图,在和中,点E、F在BC上,,,添加下列一个条件后能用“SAS”判定的是( )
A. B. C. D.
5.某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在( )
A.三条高线的交点处 B.三条中线的交点处
C.三个角的平分线的交点处 D.三条边的垂直平分线的交点处
6.如图,在中,BD是的中线,EF是BC边的垂直平分线,且BD与EF相交于点G,连结AG,CG,若四边形CDGE与四边形ACEG的面积分别为7和11,则的面积为( )
A.20 B.18 C.22 D.36
二、填空题(本题共10小题,每小题3分,共30分)
7.一个等腰三角形的两边长分别是2cm、5cm,则它的周长为______cm.
8.从镜子中看到汽车的车辆的号码如图所示,则该汽车的号码是______.
9.如图,已知在中,CD是AB边上的高线,BE平分,交CD于点E,,,则的面积等于______.
10.如图,在中.,,AB的垂直平分线分别交AB,AC于点D,E,连接BE,则的度数为_______°.
11.如图,中,,,分别以点A和点C为圆心,大于的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则的度数为_______.
12.如图,OP平分,于点A,点Q是射线OM上一个动点,若,则PQ的最小值为_______.
13.如图,在的边OA、OB上取点M、N,连接MN,PM平分,PN平分,若,的面积是2,的面积是8,则的长是_______.
14.如图,点P为内任一点,E,P分别为点P关于OA,OB的对称点.若,则_______°.
15.有三条两两相交的公路,要建一个加油站,使它到三条公路的距离相等,那么加油站可建的地点有_______个.
16.如图,在中,,,,CD为AB边上的高,点E从点B出发在直线BC上以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动______s时,.
三、解答题(本大题共10小题,共102分)
17.(8分)如图,在中,,,D为AB延长线上一点,点E在BC边上,且,连接AE、DE、DC.
求证:;
18.作图题(8分)1.(1)如图,在正方形网格中,点A、B、C都在格点上,作关于直线MN对称的图形
(2)在直线MN上找一点P,使得最小
2.如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇P,Q的距离必须相等,到两条高速公路m,n的距离也必须相等,请问发射塔应该建在什么位置?请用尺规作图在图中标记出发射塔所在的位置.
19.(10分)如图,已知线段AC,BD相交于点E,,.
(1)求证:;
(2)当时,求CD的长.
20.(10分))如图,中,,,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求的度数;
(2)若,求BC长.
21.(10分)已知:如图,E为的外角平分线上的一点,,,求证:
(1)是等腰三角形;
(2).
22.(10分)如图,在中,DM、EN分别垂直平分AC和BC交AB于M、N.
(1)若,求的周长;
(2)若,求的度数.
23.(10分)如图,在中,,P为BC的中点,D,E分别为AB,AC上的点,且.
(1)求证:.
(2)若,,求的度数.
24.(10分)已知:如图,,点D,E分别在AB、AC上,且,BE、CD交于点O,
(1)求证:;
(2)求证:点O在线段BC的垂直平分线上.
25.(12分)(1)如图①,,射线AE在这个角的内部,点B、C分别在的边AM、AN上,且,于点F,于点D.,.DF的长为____.
(2)探索证明:如图②,点B,C在的边AM、AN上,,点E,F在内部的射线AD上,且.求证:.
(3)拓展应用:如图③,在中,,.点D在边BC上,,点E、F在线段AD上,.若的面积为15,求与的面积之和.
26.(14分)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在中,,,BC边上的中线AD的取值范围.
(1)小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q使得;
②再连接BQ,把AB、AC、2AD集中在中;
③利用三角形的三边关系可得,则AD的取值范围是____.
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)请写出图1中AC与BQ的关系并证明;
(3)思考:已知,如图2,AD是的中线,,,,试探究线段AD与EF的数量和位置关系,并加以证明.
八年级数学第一次学情了解
2023926
一、单选题(本题共6小题,每小题3分,共18分)
1.下列图形中,可以被看作是轴对称图形的是( )
A. B. C. D.
2.如图,,点A与D,B与E分别是对应顶点,且测得,,则EC长为( )
A.1cm B.2cm C.3cm D.4cm
3.如图,在三角形纸片ABC中,,,,将沿过点B的直线折叠,使顶点C落在AB边上的点E处,折痕为BD,则的周长为( )
A.5cm B.6cm C.7cm D.8cm
4.如图,在和中,点E、F在BC上,,,添加下列一个条件后能用“SAS”判定的是( )
A. B. C. D.
5.某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在( )
A.三条高线的交点处 B.三条中线的交点处
C.三个角的平分线的交点处 D.三条边的垂直平分线的交点处
6.如图,在中,BD是的中线,EF是BC边的垂直平分线,且BD与EF相交于点G,连结AG,CG,若四边形CDGE与四边形ACEG的面积分别为7和11,则的面积为( )
A.20 B.18 C.22 D.36
二、填空题(本题共10小题,每小题3分,共30分)
7.一个等腰三角形的两边长分别是2cm、5cm,则它的周长为______cm.
8.从镜子中看到汽车的车辆的号码如图所示,则该汽车的号码是______.
9.如图,已知在中,CD是AB边上的高线,BE平分,交CD于点E,,,则的面积等于______.
10.如图,在中.,,AB的垂直平分线分别交AB,AC于点D,E,连接BE,则的度数为_______°.
11.如图,中,,,分别以点A和点C为圆心,大于的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则的度数为_______.
12.如图,OP平分,于点A,点Q是射线OM上一个动点,若,则PQ的最小值为_______.
13.如图,在的边OA、OB上取点M、N,连接MN,PM平分,PN平分,若,的面积是2,的面积是8,则的长是_______.
14.如图,点P为内任一点,E,P分别为点P关于OA,OB的对称点.若,则_______°.
15.有三条两两相交的公路,要建一个加油站,使它到三条公路的距离相等,那么加油站可建的地点有_______个.
16.如图,在中,,,,CD为AB边上的高,点E从点B出发在直线BC上以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动______s时,.
三、解答题(本大题共10小题,共102分)
17.(8分)如图,在中,,,D为AB延长线上一点,点E在BC边上,且,连接AE、DE、DC.
求证:;
18.作图题(8分)1.(1)如图,在正方形网格中,点A、B、C都在格点上,作关于直线MN对称的图形
(2)在直线MN上找一点P,使得最小
2.如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇P,Q的距离必须相等,到两条高速公路m,n的距离也必须相等,请问发射塔应该建在什么位置?请用尺规作图在图中标记出发射塔所在的位置.
19.(10分)如图,已知线段AC,BD相交于点E,,.
(1)求证:;
(2)当时,求CD的长.
20.(10分))如图,中,,,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求的度数;
(2)若,求BC长.
21.(10分)已知:如图,E为的外角平分线上的一点,,,求证:
(1)是等腰三角形;
(2).
22.(10分)如图,在中,DM、EN分别垂直平分AC和BC交AB于M、N.
(1)若,求的周长;
(2)若,求的度数.
23.(10分)如图,在中,,P为BC的中点,D,E分别为AB,AC上的点,且.
(1)求证:.
(2)若,,求的度数.
24.(10分)已知:如图,,点D,E分别在AB、AC上,且,BE、CD交于点O,
(1)求证:;
(2)求证:点O在线段BC的垂直平分线上.
25.(12分)(1)如图①,,射线AE在这个角的内部,点B、C分别在的边AM、AN上,且,于点F,于点D.,.DF的长为____.
(2)探索证明:如图②,点B,C在的边AM、AN上,,点E,F在内部的射线AD上,且.求证:.
(3)拓展应用:如图③,在中,,.点D在边BC上,,点E、F在线段AD上,.若的面积为15,求与的面积之和.
26.(14分)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在中,,,BC边上的中线AD的取值范围.
(1)小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q使得;
②再连接BQ,把AB、AC、2AD集中在中;
③利用三角形的三边关系可得,则AD的取值范围是____.
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)请写出图1中AC与BQ的关系并证明;
(3)思考:已知,如图2,AD是的中线,,,,试探究线段AD与EF的数量和位置关系,并加以证明.
同课章节目录
