江苏省南京市六合区励志学校2023-2024学年八年级上学期10月学情分析数学试卷(图片版,含答案)
文档属性
| 名称 | 江苏省南京市六合区励志学校2023-2024学年八年级上学期10月学情分析数学试卷(图片版,含答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 00:00:45 | ||
图片预览



文档简介
2023~2024 学年度第一学期月考学情分析样题
八年级数学
时间:100分钟 总分:100分 出卷: 审核:
一、选择题(本大题共 8小题,每小题 2分,共 16分.在每小题所给出的四个选项中,恰
有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)(王
景、金晶)
1.下列图形中,不是轴对称图形的是 ( )
A. B. C. D.
2.根据下列条件能画出唯一△ABC的是( )
A.AB=1,BC=2,CA=3 B.AB=7,BC=5,∠A=30°
C.∠A=50°,∠B=60°,∠C=70° D.AC=3.5,BC=4.8,∠C=70°
3.如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性
质,由作图所得条件,判定三角形全等运用的方法是 ( )
A. SAS B. ASA C. AAS D. SSS
4.一块三角形的草坪,现要在草坪上建一个凉亭供大家休息,要使凉亭到草坪三边的距离
相等,凉亭的位置应选在( )
A.三角形三条边的垂直平分线的交点 B.三角形三条高的交点
C.三角形三条角平分线所在直线的交点 D.三角形三条中线的交点
5.下列说法中,正确说法的个数有 ( )
①角是轴对称图形,对称轴是角的平分线;
②等腰三角形至少有 1条对称轴,至多有 3条对称轴;
③关于某直线对称的两个三角形一定是全等三角形;
④两图形关于某直线对称,对称点一定在直线的两旁.
A.1个 B.2个 C.3个 D.4个
第 1 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
6.如图,在Rt ABC中, ACB 90 , A 50 ,以点 B为圆心, BC长为半径画弧,交
AB于点D,连接CD,则 ACD的度数是 ( )
A. 50 B. 40 C. 30 D. 20
7. 如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若 AB 4,则图中阴影
部分的面积为( )
A.8 B.16 C.32 D.64
8. 勾股定理的验证方法很多,用面积(拼图)证明是最常见的一种方法.如图所示,一个
直立的长方体在桌面上慢慢地倒下,启发人们想到勾股定理的证明方法,设 AB c,BC a,
AC b,证明中用到的面积相等关系是( )
A. S△ABC S△ABD S△AFG S△AEF
B. S BCEF S△ABC S△ABF S△AEF S梯形 △FGH
C. S梯形BCEF S△ABC S△ABF S△AEF
D. S△BDH S△FGH
第 2 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
二、填空题(本大题共 10小题,每小题 2分,共 20分.不需写出解答过程,请把答案直接
填写在答题卡相应位置上)(王景、金晶)
9. 角的对称轴是 .
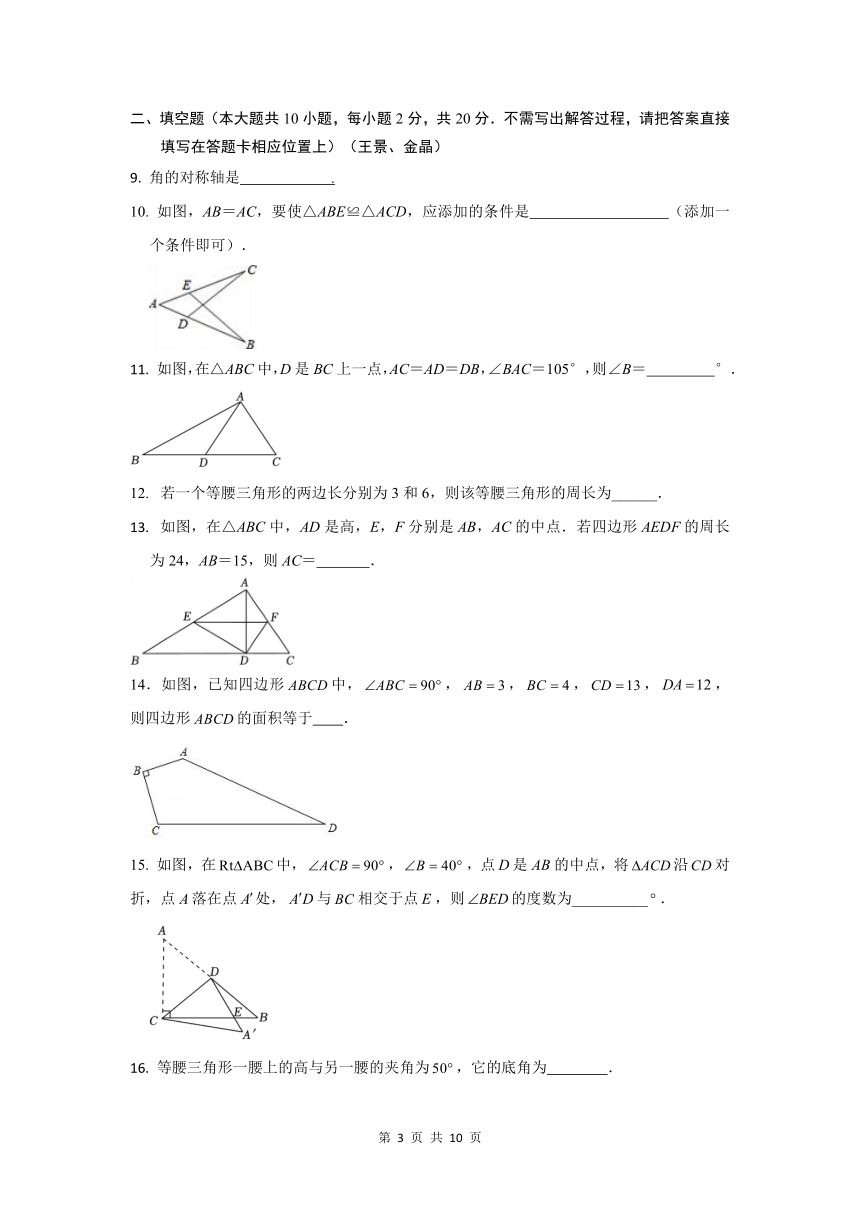
10. 如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 (添加一
个条件即可).
11. 如图,在△ABC中,D是 BC上一点,AC=AD=DB,∠BAC=105°,则∠B= °.
12. 若一个等腰三角形的两边长分别为 3和 6,则该等腰三角形的周长为______.
13. 如图,在△ABC中,AD是高,E,F分别是 AB,AC的中点.若四边形 AEDF的周长
为 24,AB=15,则 AC= .
14.如图,已知四边形 ABCD中, ABC 90 , AB 3, BC 4,CD 13, DA 12,
则四边形 ABCD的面积等于 .
15. 如图,在Rt ABC中, ACB 90 , B 40 ,点D是 AB的中点,将 ACD沿CD对
折,点 A落在点 A 处, A D与 BC相交于点 E,则 BED的度数为__________ .
16. 等腰三角形一腰上的高与另一腰的夹角为 50 ,它的底角为 .
第 3 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
17. 数学家赵爽在注解《周髀算经》时给出了“赵爽弦图”,如图所示,它是由四个全等的
直角三角形和一个小正方形拼成的一个大正方形,若直角三角形较短直角边长为 6,大正
方形的边长为 10,则小正方形的面积为 .
18.如图所示,等腰三角形 ABC的底边为8cm,腰长为 5cm,一动点 P(与 B、C 不重合)
在底边上从 B向C以1cm / s的速度移动,当 P运动 秒时, ACP是直角三角形.
三、解答题(本大题共 8小题,共 64分.请在答题卡指定区域内作答,解答时应写出文字
说明、证明过程或演算步骤)(骆开良、罗锐)
19.(6 分)已知:如图,△ABC≌△DCB, AC、DB相交于点 E.求证: AE DE.
20.(6 分)如图,方格纸中每个小方格都是边长为 1的正方形,我们把以格点连线为边的多
边形称为“格点多边形”.如图所示,四边形 ABCD就是一个“格点四边形”.
(1)作出四边形 ABCD关于直线 BD对称的四边形 A′B′C′D′;
(2)四边形 ABCD的面积为______;
第 4 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
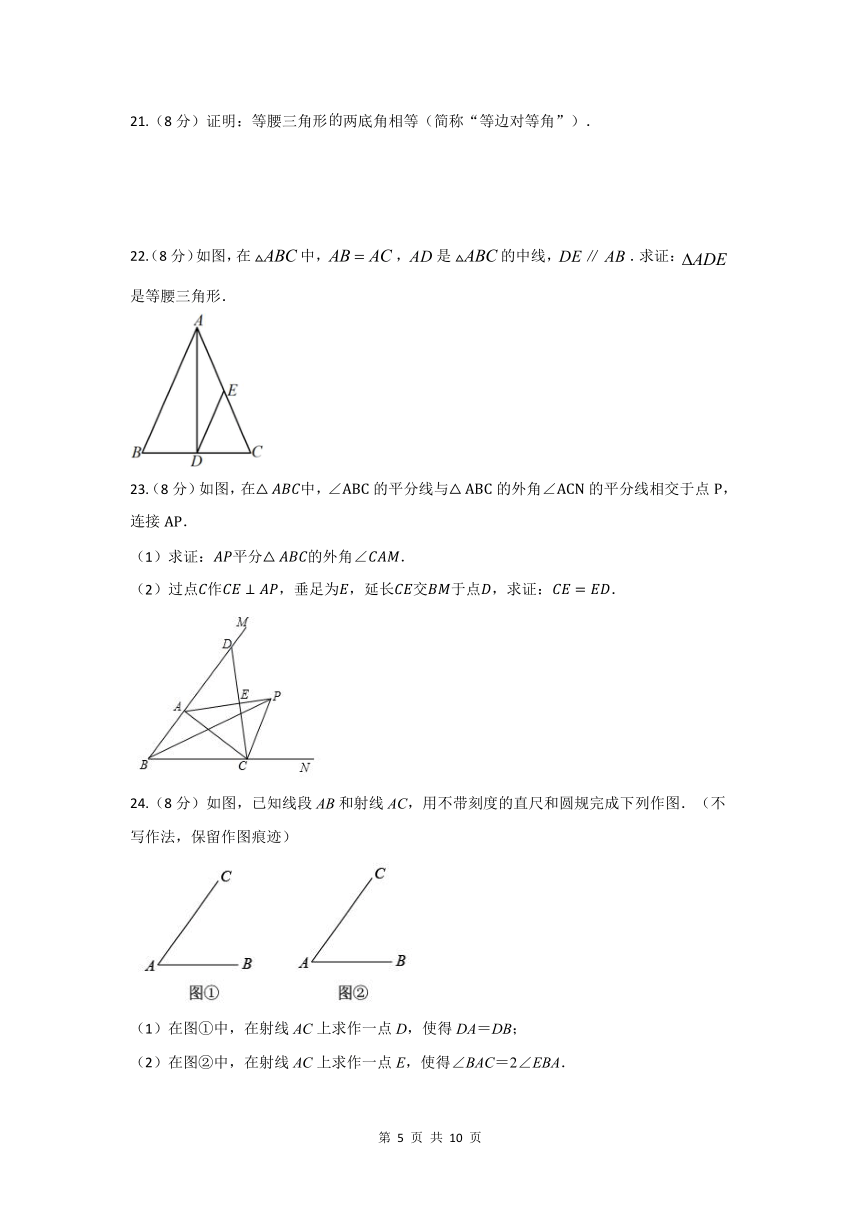
21.(8 分)证明:等腰三角形的两底角相等(简称“等边对等角”).
22(. 8 分)如图,在 ABC中,AB AC,AD是 ABC的中线,DE∥ AB.求证: ADE
是等腰三角形.
23.(8 分)如图,在△ 中,∠ABC的平分线与△ ABC的外角∠ACN的平分线相交于点 P,
连接 AP.
(1)求证: 平分△ 的外角∠ .
(2)过点 作 ⊥ ,垂足为 ,延长 交 于点 ,求证: = .
24.(8 分)如图,已知线段 AB和射线 AC,用不带刻度的直尺和圆规完成下列作图.(不
写作法,保留作图痕迹)
(1)在图①中,在射线 AC上求作一点 D,使得 DA=DB;
(2)在图②中,在射线 AC上求作一点 E,使得∠BAC=2∠EBA.
第 5 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
25.(8 分)已知:△ACB和 都是等腰直角三角形, ACB ECD 90 ,点D在 AB
的延长线上.
求证:(1) E=BD
(2) BD2 AD2 ED2.
26.(12 分)如图,点 P、Q分别是等边△ 边 、 上的动点(端点除外),点 P、点
Q以相同的速度,同时从点 A、点 B出发.
(1)如图 1,连接 AQ、CP.求证:△ ABQ ≌△ CAP;
(2)如图 1,当点 P、Q分别在 AB、BC边上运动时,AQ、CP相交于点 M,∠QMC的大小
是否变化?若变化,请说明理由;若不变,求出它的度数;
(3)如图 2,当点 P、Q 在 AB、BC 的延长线上运动时,直线 AQ、CP 相交于 M,∠QMC
的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
第 6 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
2023~2024 学年度第一学期月考学情分析样题
八年级数学参考答案及评分标准
一、选择题(本大题共 8 小题,每小题 2 分,共 16 分)
题号 1 2 3 4 5 6 7 8
答案 A D D C B D B C
二、填空题(本大题共 10 小题,每题2 分,共20 分)
9. 角平分线所在直线 10. AD=AE(答案不唯一) 11. 25° 12.15 13. 9
14. 36 15 . 120° 16. 20°或70° 17. 4 18. 1.75或4
三、解答题(本大题共 8小题,共 64分.)
19.证明:∵△ABC≌△DCB,
∴∠A=∠D,AB=DC,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS).
∴AE=DE.
20.解:(1)如图所示:
.
(2)S 四边形 ABCD=S△ABC+S△ADC= ×4×2+ ×4×4=4+8=12;
21.已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C.
证明:过点 A作 AD⊥BC,垂足为 D,
第 7 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在 Rt△ADB和 Rt△ADC中,AD=AD,AB=AC,
∴Rt△ADB≌Rt△ADC(HL),
∴∠B=∠C(方法不唯一)
22.证明:∵AB=AC,AD是△ABC的中线,
∴∠BAD=∠CAD,
∵DE∥AB,
∴∠ADE=∠BAD,
∴∠CAD=∠ADE,
∴DE=AE,
∴△ADE是等腰三角形.
23 证明:(1)过 P作 PT⊥BC于 T,PS⊥AC于 S,PQ⊥BA于 Q,如图,
∵在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点 P,
∴PQ=PT,PS=PT,
∴PQ=PS,
∴AP平分∠DAC,
即 PA平分∠BAC的外角∠CAM;
(2)∵PA平分∠BAC的外角∠CAM,
∴∠DAE=∠CAE,
∵CE⊥AP,
∴∠AED=∠AEC=90°,
在△AED和△AEC中
第 8 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
∴△AED≌△AEC(ASA),
∴CE=ED.
24.解:(1)如图①,点 D为所作;
(2)如图②,点 E为所作.
25.证明:(1)∵△ACB和△ECD都是等腰直角三角形,
∴AC=BC,AE=BD,∠ACB=∠ECD=90°,∠CAB=∠CBA=45°,
∴∠ACE=∠BCD,∠CBD=135°,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴BD=AE,
(2)∵∠CBD=∠CAE=135°
∴∠EAD=135°—45°=90°,
∴ED2=AE2+AD2,
∴ED2=BD2+AD2.
第 9 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
26.解:(1)证明:如图 1,∵△ABC是等边三角形
∴∠ABQ=∠CAP=60°,AB=CA,
又∵点 P、Q运动速度相同,
∴AP=BQ,
在△ABQ与△CAP中,
,
∴△ABQ≌△CAP(SAS);
(2)点 P、Q在 AB、BC边上运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC是△ACM的外角,
∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC
∵∠BAC=60°,
∴∠QMC=60°;
(3)如图 2,点 P、Q在运动到终点后继续在射线 AB、BC上运动时,∠QMC不变
理由:同理可得,△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC是△APM的外角,
∴∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°﹣∠PAC=180°﹣60°=120°,
即若点 P、Q在运动到终点后继续在射线 AB、BC上运动,∠QMC的度数为 120°.
第 10 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
八年级数学
时间:100分钟 总分:100分 出卷: 审核:
一、选择题(本大题共 8小题,每小题 2分,共 16分.在每小题所给出的四个选项中,恰
有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)(王
景、金晶)
1.下列图形中,不是轴对称图形的是 ( )
A. B. C. D.
2.根据下列条件能画出唯一△ABC的是( )
A.AB=1,BC=2,CA=3 B.AB=7,BC=5,∠A=30°
C.∠A=50°,∠B=60°,∠C=70° D.AC=3.5,BC=4.8,∠C=70°
3.如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性
质,由作图所得条件,判定三角形全等运用的方法是 ( )
A. SAS B. ASA C. AAS D. SSS
4.一块三角形的草坪,现要在草坪上建一个凉亭供大家休息,要使凉亭到草坪三边的距离
相等,凉亭的位置应选在( )
A.三角形三条边的垂直平分线的交点 B.三角形三条高的交点
C.三角形三条角平分线所在直线的交点 D.三角形三条中线的交点
5.下列说法中,正确说法的个数有 ( )
①角是轴对称图形,对称轴是角的平分线;
②等腰三角形至少有 1条对称轴,至多有 3条对称轴;
③关于某直线对称的两个三角形一定是全等三角形;
④两图形关于某直线对称,对称点一定在直线的两旁.
A.1个 B.2个 C.3个 D.4个
第 1 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
6.如图,在Rt ABC中, ACB 90 , A 50 ,以点 B为圆心, BC长为半径画弧,交
AB于点D,连接CD,则 ACD的度数是 ( )
A. 50 B. 40 C. 30 D. 20
7. 如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若 AB 4,则图中阴影
部分的面积为( )
A.8 B.16 C.32 D.64
8. 勾股定理的验证方法很多,用面积(拼图)证明是最常见的一种方法.如图所示,一个
直立的长方体在桌面上慢慢地倒下,启发人们想到勾股定理的证明方法,设 AB c,BC a,
AC b,证明中用到的面积相等关系是( )
A. S△ABC S△ABD S△AFG S△AEF
B. S BCEF S△ABC S△ABF S△AEF S梯形 △FGH
C. S梯形BCEF S△ABC S△ABF S△AEF
D. S△BDH S△FGH
第 2 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
二、填空题(本大题共 10小题,每小题 2分,共 20分.不需写出解答过程,请把答案直接
填写在答题卡相应位置上)(王景、金晶)
9. 角的对称轴是 .
10. 如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 (添加一
个条件即可).
11. 如图,在△ABC中,D是 BC上一点,AC=AD=DB,∠BAC=105°,则∠B= °.
12. 若一个等腰三角形的两边长分别为 3和 6,则该等腰三角形的周长为______.
13. 如图,在△ABC中,AD是高,E,F分别是 AB,AC的中点.若四边形 AEDF的周长
为 24,AB=15,则 AC= .
14.如图,已知四边形 ABCD中, ABC 90 , AB 3, BC 4,CD 13, DA 12,
则四边形 ABCD的面积等于 .
15. 如图,在Rt ABC中, ACB 90 , B 40 ,点D是 AB的中点,将 ACD沿CD对
折,点 A落在点 A 处, A D与 BC相交于点 E,则 BED的度数为__________ .
16. 等腰三角形一腰上的高与另一腰的夹角为 50 ,它的底角为 .
第 3 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
17. 数学家赵爽在注解《周髀算经》时给出了“赵爽弦图”,如图所示,它是由四个全等的
直角三角形和一个小正方形拼成的一个大正方形,若直角三角形较短直角边长为 6,大正
方形的边长为 10,则小正方形的面积为 .
18.如图所示,等腰三角形 ABC的底边为8cm,腰长为 5cm,一动点 P(与 B、C 不重合)
在底边上从 B向C以1cm / s的速度移动,当 P运动 秒时, ACP是直角三角形.
三、解答题(本大题共 8小题,共 64分.请在答题卡指定区域内作答,解答时应写出文字
说明、证明过程或演算步骤)(骆开良、罗锐)
19.(6 分)已知:如图,△ABC≌△DCB, AC、DB相交于点 E.求证: AE DE.
20.(6 分)如图,方格纸中每个小方格都是边长为 1的正方形,我们把以格点连线为边的多
边形称为“格点多边形”.如图所示,四边形 ABCD就是一个“格点四边形”.
(1)作出四边形 ABCD关于直线 BD对称的四边形 A′B′C′D′;
(2)四边形 ABCD的面积为______;
第 4 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
21.(8 分)证明:等腰三角形的两底角相等(简称“等边对等角”).
22(. 8 分)如图,在 ABC中,AB AC,AD是 ABC的中线,DE∥ AB.求证: ADE
是等腰三角形.
23.(8 分)如图,在△ 中,∠ABC的平分线与△ ABC的外角∠ACN的平分线相交于点 P,
连接 AP.
(1)求证: 平分△ 的外角∠ .
(2)过点 作 ⊥ ,垂足为 ,延长 交 于点 ,求证: = .
24.(8 分)如图,已知线段 AB和射线 AC,用不带刻度的直尺和圆规完成下列作图.(不
写作法,保留作图痕迹)
(1)在图①中,在射线 AC上求作一点 D,使得 DA=DB;
(2)在图②中,在射线 AC上求作一点 E,使得∠BAC=2∠EBA.
第 5 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
25.(8 分)已知:△ACB和 都是等腰直角三角形, ACB ECD 90 ,点D在 AB
的延长线上.
求证:(1) E=BD
(2) BD2 AD2 ED2.
26.(12 分)如图,点 P、Q分别是等边△ 边 、 上的动点(端点除外),点 P、点
Q以相同的速度,同时从点 A、点 B出发.
(1)如图 1,连接 AQ、CP.求证:△ ABQ ≌△ CAP;
(2)如图 1,当点 P、Q分别在 AB、BC边上运动时,AQ、CP相交于点 M,∠QMC的大小
是否变化?若变化,请说明理由;若不变,求出它的度数;
(3)如图 2,当点 P、Q 在 AB、BC 的延长线上运动时,直线 AQ、CP 相交于 M,∠QMC
的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
第 6 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
2023~2024 学年度第一学期月考学情分析样题
八年级数学参考答案及评分标准
一、选择题(本大题共 8 小题,每小题 2 分,共 16 分)
题号 1 2 3 4 5 6 7 8
答案 A D D C B D B C
二、填空题(本大题共 10 小题,每题2 分,共20 分)
9. 角平分线所在直线 10. AD=AE(答案不唯一) 11. 25° 12.15 13. 9
14. 36 15 . 120° 16. 20°或70° 17. 4 18. 1.75或4
三、解答题(本大题共 8小题,共 64分.)
19.证明:∵△ABC≌△DCB,
∴∠A=∠D,AB=DC,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS).
∴AE=DE.
20.解:(1)如图所示:
.
(2)S 四边形 ABCD=S△ABC+S△ADC= ×4×2+ ×4×4=4+8=12;
21.已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C.
证明:过点 A作 AD⊥BC,垂足为 D,
第 7 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在 Rt△ADB和 Rt△ADC中,AD=AD,AB=AC,
∴Rt△ADB≌Rt△ADC(HL),
∴∠B=∠C(方法不唯一)
22.证明:∵AB=AC,AD是△ABC的中线,
∴∠BAD=∠CAD,
∵DE∥AB,
∴∠ADE=∠BAD,
∴∠CAD=∠ADE,
∴DE=AE,
∴△ADE是等腰三角形.
23 证明:(1)过 P作 PT⊥BC于 T,PS⊥AC于 S,PQ⊥BA于 Q,如图,
∵在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点 P,
∴PQ=PT,PS=PT,
∴PQ=PS,
∴AP平分∠DAC,
即 PA平分∠BAC的外角∠CAM;
(2)∵PA平分∠BAC的外角∠CAM,
∴∠DAE=∠CAE,
∵CE⊥AP,
∴∠AED=∠AEC=90°,
在△AED和△AEC中
第 8 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
∴△AED≌△AEC(ASA),
∴CE=ED.
24.解:(1)如图①,点 D为所作;
(2)如图②,点 E为所作.
25.证明:(1)∵△ACB和△ECD都是等腰直角三角形,
∴AC=BC,AE=BD,∠ACB=∠ECD=90°,∠CAB=∠CBA=45°,
∴∠ACE=∠BCD,∠CBD=135°,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴BD=AE,
(2)∵∠CBD=∠CAE=135°
∴∠EAD=135°—45°=90°,
∴ED2=AE2+AD2,
∴ED2=BD2+AD2.
第 9 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
26.解:(1)证明:如图 1,∵△ABC是等边三角形
∴∠ABQ=∠CAP=60°,AB=CA,
又∵点 P、Q运动速度相同,
∴AP=BQ,
在△ABQ与△CAP中,
,
∴△ABQ≌△CAP(SAS);
(2)点 P、Q在 AB、BC边上运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC是△ACM的外角,
∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC
∵∠BAC=60°,
∴∠QMC=60°;
(3)如图 2,点 P、Q在运动到终点后继续在射线 AB、BC上运动时,∠QMC不变
理由:同理可得,△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC是△APM的外角,
∴∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°﹣∠PAC=180°﹣60°=120°,
即若点 P、Q在运动到终点后继续在射线 AB、BC上运动,∠QMC的度数为 120°.
第 10 页 共 10 页
{#{QQABIYAQggCAAABAAAhCQwESCAEQkAEACIoOwFAAMAAAgRNABAA=}#}
同课章节目录
