专题26.2反比例函数 基础篇专项练习(含解析)2023-2024学年九年级数学下册人教版专项讲练
文档属性
| 名称 | 专题26.2反比例函数 基础篇专项练习(含解析)2023-2024学年九年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 407.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 22:43:05 | ||
图片预览




文档简介
专题26.2 反比例函数(基础篇)(专项练习)
一、单选题
1.下列函数:①y=2x,②y=,③y=x﹣1,④y=.其中,是反比例函数的有( ).
A.0个 B.1个 C.2个 D.3个
2.已知反比例函数的图象过,则它的图象一定不经过点( ).
A. B. C. D.
3.如果函数反比例函数,那么的值是( )
A.2 B. C.1 D.0
4.若反比例函数的图象经过点,则a的值为( ).
A. B. C. D.
5.已知点A(3,4)在反比例函数为常数,的图象上,则该反比例函数的解析式是( )
A. B.y= C. y= D. y=
6.若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
7.反比例函数y=的图象经过点(3,﹣2),下列各点在图象上的是( )
A.(﹣3,﹣2) B.(3,2) C.(﹣2,﹣3) D.(﹣2,3)
8.用电器的输出功率与通过的电流、用电器的电阻之间的关系是,下面说法正确的是( )
A.为定值,与成反比例 B.为定值,与成反比例
C.为定值,与成正比例 D.为定值,与成正比例
9.某品牌的饮水机接通电源就进入自动程序:开机加热到水温100,停止加热,水温开始下降,此时水温()与开机后用时(min)成反比例关系,直至水温降至30,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若水温为30时接通电源,水温y()和时间x(min)的关系如图所示,则水温从100降到35所用的时间是( )
A.27min B.20min C.13min D.12min
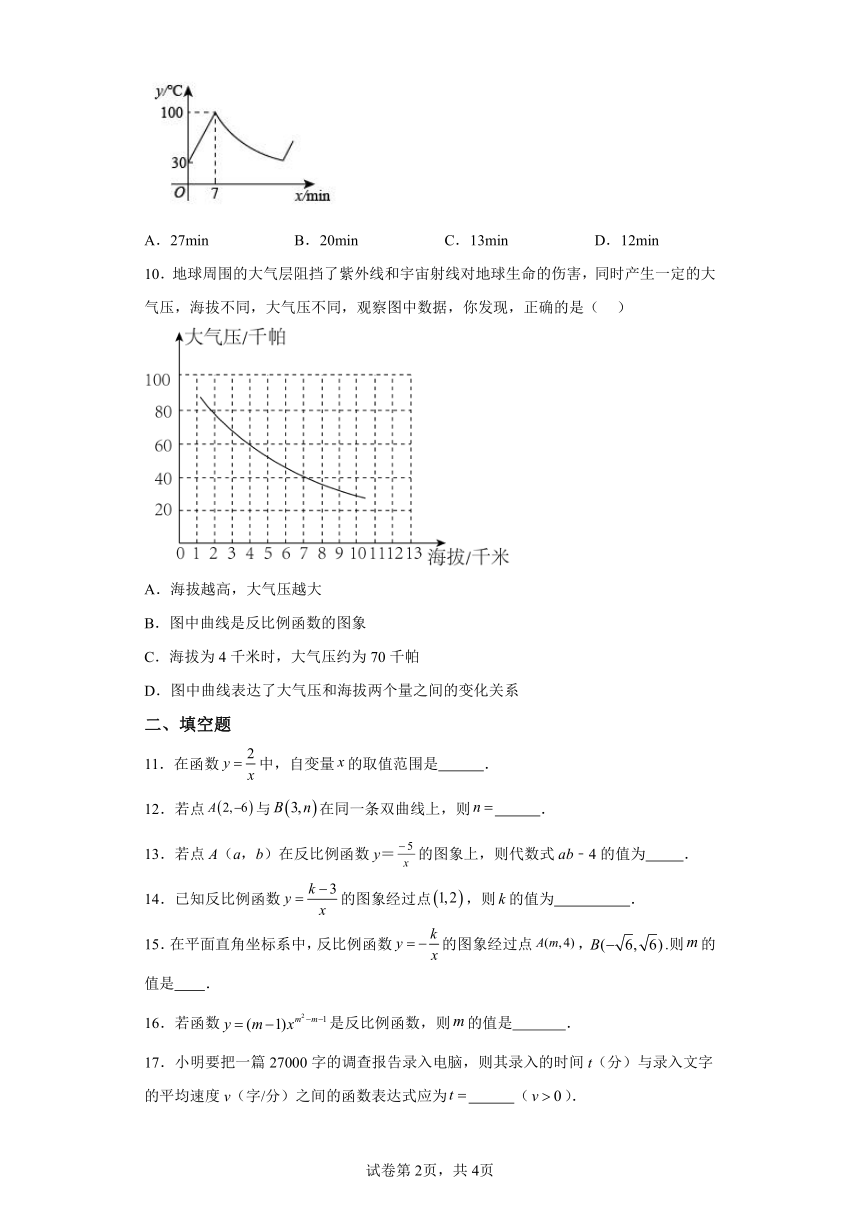
10.地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害,同时产生一定的大气压,海拔不同,大气压不同,观察图中数据,你发现,正确的是( )
A.海拔越高,大气压越大
B.图中曲线是反比例函数的图象
C.海拔为4千米时,大气压约为70千帕
D.图中曲线表达了大气压和海拔两个量之间的变化关系
二、填空题
11.在函数中,自变量的取值范围是 .
12.若点与在同一条双曲线上,则 .
13.若点A(a,b)在反比例函数y=的图象上,则代数式ab﹣4的值为 .
14.已知反比例函数的图象经过点,则的值为 .
15.在平面直角坐标系中,反比例函数的图象经过点,.则的值是 .
16.若函数是反比例函数,则的值是 .
17.小明要把一篇27000字的调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为 ().
18.如图,的顶点C在反比例函数的图像上,且点A坐标为,点B坐标为,则k的值为 .
三、解答题
19.下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
(1)
(2)
(3)
(4)xy=1
(5)
20.写出下列问题中的函数关系式,并判断它们是否为反比例函数.
(1)某农场的粮食总产量为1500t,该农场人数y(人)与平均每人占有粮食量x(t)的函数关系式;
(2)在加油站,加油机显示器上显示的某一种油的单价为6.75元,总价从0元开始随着加油量的变化而变化,总价y(元)与加油量x(L)的函数关系式.
21.已知,与成正比例,与成反比例,当时,;当时,.
(1)求与之间的函数关系式;
(2)当时,求的值.
22.在平面直角坐标系xOy中,若反比例函数的图象经过点和点,求m的值.
23.已知y是x的反比例函数,下表列出了x与y的一些对应值.
x … -4 -3 -2 -1 2 3 …
y … 6 -18 …
(1)写出这个反比例函数的表达式;
(2)根据表达式完成上表.
24.若分式方程的解为,试判断点和点是否在反比例函数的图像上.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据反比例函数的定义,逐项分析判断即可.解析式符合的形式为反比例函数.
【详解】解:①y是x正比例函数;
②y是x反比例函数;
③y是x反比例函数;
④y是x+1的反比例函数.
综上所述,是反比例函数的有②③,共计2个
故选:C.
【点睛】本题考查了反比例函数的定义,将一般转化为y=kx﹣1,是解题的关键.
2.A
【分析】根据反比例函数的定义可直接进行求解.
【详解】解:设该反比例函数为,则有:
∵反比例函数的图象过,
∴,
∴选项A的点一定不经过该反比例函数;
故选A.
【点睛】本题主要考查反比例函数的定义,熟练掌握反比例函数的定义是解题的关键.
3.B
【分析】根据反比例函数的定义,即y=(k≠0),只需令、m-1≠0即可.
【详解】解:∵是反比例函数,
∴,
解得:,故B正确.
故选:B.
【点睛】本题考查了反比例函数的定义,重点是将一般式y=(k≠0)转化为y=kx 1(k≠0)的形式.
4.C
【分析】把点的坐标代入函数解析式,解方程即可.
【详解】解:把代入,得,
解得,,
故选:C.
【点睛】本题考查了反比例函数图象上点的坐标,解题关键是明确反比例函数图象上点的坐标满足函数解析式.
5.C
【分析】直接把点A(3,4)代入反比例函数y=,求出k的值即可.
【详解】解:∵将点A(3,4)代入反比例函数y=,得4=,
解得k=12.
∴反比例函数表达式为:y=,
故选:C.
【点睛】本题考查的是待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
6.B
【分析】将A、B、C三点坐标分别代入反比例函数的解析式,求出的值比较其大小即可
【详解】∵点,,都在反比例函数的图象上,
∴分别把x=-3、x=-2、x=1代入得,,
∴
故选B
【点睛】本题考查了反比例函数的图像和性质,熟练掌握相关的知识点是解题的关键.
7.D
【分析】直接利用反比例函数图象上点的坐标特点进而得出答案.
【详解】解:∵反比例函数y=的图象经过点(3,-2),
∴xy=k=-6,
A、(-3,-2),此时xy=-3×(-2)=6,不合题意;
B、(3,2),此时xy=3×2=6,不合题意;
C、(-2,-3),此时xy=-3×(-2)=6,不合题意;
D、(-2,3),此时xy=-2×3=-6,符合题意;
故选D.
【点睛】此题主要考查了反比例函数图象上点的坐标特征,正确得出k的值是解题关键.
8.B
【详解】解:当为定值时,2与的乘积是定值,所以 2与成反比例.
故选:B.
9.C
【分析】先求出水温开始下降时,水温y()与开机后用时x(min)的反比例函数解析式,再求出水温为35时的时间,计算即可.
【详解】解:设水温开始下降时,水温y()与开机后用时x(min)的反比例解析式为,
代入(7,100)得:,即,
当y=35时,即,
解得:,
∵20-7=13,
∴水温从100降到35所用的时间是13 min,
故选:C.
【点睛】本题考查了求反比例函数解析式,反比例函数图像上点的坐标特征,熟练掌握待定系数法是解题的关键.
10.D
【分析】根据图象中的数据回答即可.
【详解】解:A.海拔越高,大气压越小,该选项不符合题意;
B.∵图象经过点(2,80),(4,60),
∴2×80=160,4×60=240,而160≠240,
∴图中曲线不是反比例函数的图象,该选项不符合题意;
C.∵图象经过点 (4,60),
∴海拔为4千米时,大气压约为60千帕,该选项不符合题意;
D.图中曲线表达了大气压和海拔两个量之间的变化关系,该选项符合题意;
故选:D.
【点睛】本题考查了函数的图象,解题的关键是读懂题意,能正确识图.
11.
【分析】根据反比例函数的定义,即可得到答案.
【详解】解:由题意得:在函数中,,
故答案是:.
【点睛】本题主要考查反比函数自变量取值范围,掌握反比例函数自变量不等于0,是解题的关键.
12.
【分析】设反比例函数解析式为(k≠0),由A点求得k,再由B点横坐标求得纵坐标即可.
【详解】解:设反比例函数解析式为(k≠0),
由点A(2,-6)可得k=xy=-12,
∴,
当x=3时,,
即B(3,-4),
故答案为:-4.
【点睛】本题考查了反比例函数解析式,掌握待定系数法求函数解析式是解题关键.
13.-9
【分析】由点A在反比例函数图象上,可得出ab=-5,将其代入代数式ab-4中即可得出结论.
【详解】解:∵点A(a,b)在反比例函数y=的图象上
∴ab=-5
∴ab-4=-5-4=-9.
故答案为:-9.
【点睛】本题考查了反比例函数图象上点的坐标特征,解题的关键是找出ab=2.本题属于基础题,难度不大,解决该题型题目时,由点在反比例函数图象上可以得出点的横纵坐标之积为定值,将其代入代数式即可.
14.5
【分析】把点的坐标代入函数解析式得出方程,求出方程的解即可.
【详解】解:∵反比例函数的图象经过点(1,2),
∴将(1,2)代入得:k 3=2,
解得:k=5,
故答案为:5.
【点睛】本题考查了反比例函数图象上点的坐标特征,能根据已知得出关于k的方程是解此题的关键.
15.
【分析】将点B的坐标代入反比例函数解析式,得出k的值,再将点A的纵坐标代入即可得出m的值.
【详解】解:将点B的坐标代入反比例函数解析式,得出:,
∴,
将点A的纵坐标代入可得,,解得,.
故答案为:.
【点睛】本题考查的知识点是反比例函数图象上点的坐标,属于基础题目,易于掌握.
16.0
【分析】根据反比例函数的定义,即可求解.
【详解】解:∵函数是反比例函数,
∴且,
解得:m=0.
故答案为:0
【点睛】本题主要考查了反比例函数的定义,解一元二次方程,熟练掌握形如或的形式的函数关系,称为反比例函数是解题的关键.
17.
【分析】根据录入的时间=录入总量÷录入速度即可得出函数关系式.
【详解】解:由录入的时间=录入总量÷录入速度,
可得t(v>0).
故答案为:.
【点睛】本题考查了根据实际问题列函数关系式的知识,比较简单,解答本题的关键是掌握关系式录入的时间=录入总量÷录入速度.
18.8
【分析】由于四边形OABC为平行四边形,根据平移的性质,结合点O、A、B的坐标可确定点C的坐标为(4,2),将其代入带反比例函数解析式求k值即可.
【详解】解:∵四边形OABC为平行四边形,
∴,,
∵A坐标为,点B坐标为,点O坐标为,
由平移的性质可知,点C的坐标为(4,2),
∴将点C(4,2)代入到函数中,
可得,解得.
故答案为:8.
【点睛】本题主要考查了反比例函数图像上点的坐标特征、平行四边形的性质及平移的性质,解题关键是确定C点的坐标.
19.(1)是,;
(2)是,;
(3)否;
(4)是,(可化为);
(5)是,
【分析】利用反比例函数的定义判定即可.
【详解】(1)解:是反比例函数,比例系数;
(2)解:是反比例函数,比例系数;
(3)解:不是反比例函数;
(4)解:∵xy=1,
∴,
∴y是x的反比例函数,比例系数;
(5)解:是反比例函数;比例系数;
【点睛】本题主要考查了反比例函数的定义,解题的关键是熟记反比例函数的定义,反比例函数解析式的一般式y=(k≠0).
20.(1),是反比例函数;(2),是正比例函数,不是反比例函数.
【分析】(1)根据题意列出函数关系式,然后根据反比例函数的定义判断即可;
(2)根据题意列出函数关系式,然后根据正比例函数的定义判断即可;
【详解】(1)由题意,得是反比例函数;
(2)由单价乘以加油量等于总价,得,是正比例函数,不是反比例函数.
【点睛】本题考查了反比例函数与正比例函数的定义,根据题意列出函数关系式是解题关键.
21.(1);(2)
【分析】(1)设,则有,然后把当时,;当时,代入求解即可;
(2)由(1)可直接把x=3代入求解.
【详解】解:(1)设,由可得:,
∴把,和,代入得:
,解得:,
∴y与x的函数解析式为:;
(2)由(1)可把x=3代入得:
.
【点睛】本题主要考查反比例函数的定义及函数解析式,熟练掌握反比例函数的定义及求函数解析式的方法是解题的关键.
22.-3
【分析】由反比例函数的图象及其性质将A、B点代入反比例函数即可求得m的值为-3.
【详解】∵反比例函数的图象经过点,
∴.
∵点在反比例函数的图象上,
∴,
解得:.
故m的轴为-3.
【点睛】本题考查了反比例函数值的求法,明确图象上点的坐标和解析式的关系是解题的关键.
23.(1);(2)见解析
【分析】(1)设反比例函数的表达式为y=,找出函数图象上一个点的坐标,然后代入求解即可;
(2)将x或y的值代入函数解析式求得对应的y或x的值即可.
【详解】解:(1)设反比例函数的表达式为y=,
把代入得,
(2)将y=代入得:;
将代入得:y=;
将代入得:y=9;
将代入得:y=18,
将代入得:x=1;
将x=2代入得:,
将x=3代入得:.
【点睛】本题主要考查的是反比例函数的定义、函数图象上点的坐标与函数解析式之间的关系,求得函数的解析式是解题的关键.
24.点不在反比例函数的图像上,点在反比例函数的图像上
【分析】解分式方程得出的值,将其带入点和点,得出两点的坐标,再验证两点坐标是否在反比例函数上即可得出答案.
【详解】解:由题,解方程
去分母,得,即,解得,
经检验是原分式方程的解,
∴
∵反比例函数,
∴
∵,
∴,
∴点不在反比例函数的图像上,点在反比例函数的图像上.
【点睛】本题考查解分式方程,以及判断坐标系中点是否在反比例函数上,熟练掌握解分式方程的步骤,尤其注意检验是本题解题关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列函数:①y=2x,②y=,③y=x﹣1,④y=.其中,是反比例函数的有( ).
A.0个 B.1个 C.2个 D.3个
2.已知反比例函数的图象过,则它的图象一定不经过点( ).
A. B. C. D.
3.如果函数反比例函数,那么的值是( )
A.2 B. C.1 D.0
4.若反比例函数的图象经过点,则a的值为( ).
A. B. C. D.
5.已知点A(3,4)在反比例函数为常数,的图象上,则该反比例函数的解析式是( )
A. B.y= C. y= D. y=
6.若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
7.反比例函数y=的图象经过点(3,﹣2),下列各点在图象上的是( )
A.(﹣3,﹣2) B.(3,2) C.(﹣2,﹣3) D.(﹣2,3)
8.用电器的输出功率与通过的电流、用电器的电阻之间的关系是,下面说法正确的是( )
A.为定值,与成反比例 B.为定值,与成反比例
C.为定值,与成正比例 D.为定值,与成正比例
9.某品牌的饮水机接通电源就进入自动程序:开机加热到水温100,停止加热,水温开始下降,此时水温()与开机后用时(min)成反比例关系,直至水温降至30,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若水温为30时接通电源,水温y()和时间x(min)的关系如图所示,则水温从100降到35所用的时间是( )
A.27min B.20min C.13min D.12min
10.地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害,同时产生一定的大气压,海拔不同,大气压不同,观察图中数据,你发现,正确的是( )
A.海拔越高,大气压越大
B.图中曲线是反比例函数的图象
C.海拔为4千米时,大气压约为70千帕
D.图中曲线表达了大气压和海拔两个量之间的变化关系
二、填空题
11.在函数中,自变量的取值范围是 .
12.若点与在同一条双曲线上,则 .
13.若点A(a,b)在反比例函数y=的图象上,则代数式ab﹣4的值为 .
14.已知反比例函数的图象经过点,则的值为 .
15.在平面直角坐标系中,反比例函数的图象经过点,.则的值是 .
16.若函数是反比例函数,则的值是 .
17.小明要把一篇27000字的调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为 ().
18.如图,的顶点C在反比例函数的图像上,且点A坐标为,点B坐标为,则k的值为 .
三、解答题
19.下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
(1)
(2)
(3)
(4)xy=1
(5)
20.写出下列问题中的函数关系式,并判断它们是否为反比例函数.
(1)某农场的粮食总产量为1500t,该农场人数y(人)与平均每人占有粮食量x(t)的函数关系式;
(2)在加油站,加油机显示器上显示的某一种油的单价为6.75元,总价从0元开始随着加油量的变化而变化,总价y(元)与加油量x(L)的函数关系式.
21.已知,与成正比例,与成反比例,当时,;当时,.
(1)求与之间的函数关系式;
(2)当时,求的值.
22.在平面直角坐标系xOy中,若反比例函数的图象经过点和点,求m的值.
23.已知y是x的反比例函数,下表列出了x与y的一些对应值.
x … -4 -3 -2 -1 2 3 …
y … 6 -18 …
(1)写出这个反比例函数的表达式;
(2)根据表达式完成上表.
24.若分式方程的解为,试判断点和点是否在反比例函数的图像上.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据反比例函数的定义,逐项分析判断即可.解析式符合的形式为反比例函数.
【详解】解:①y是x正比例函数;
②y是x反比例函数;
③y是x反比例函数;
④y是x+1的反比例函数.
综上所述,是反比例函数的有②③,共计2个
故选:C.
【点睛】本题考查了反比例函数的定义,将一般转化为y=kx﹣1,是解题的关键.
2.A
【分析】根据反比例函数的定义可直接进行求解.
【详解】解:设该反比例函数为,则有:
∵反比例函数的图象过,
∴,
∴选项A的点一定不经过该反比例函数;
故选A.
【点睛】本题主要考查反比例函数的定义,熟练掌握反比例函数的定义是解题的关键.
3.B
【分析】根据反比例函数的定义,即y=(k≠0),只需令、m-1≠0即可.
【详解】解:∵是反比例函数,
∴,
解得:,故B正确.
故选:B.
【点睛】本题考查了反比例函数的定义,重点是将一般式y=(k≠0)转化为y=kx 1(k≠0)的形式.
4.C
【分析】把点的坐标代入函数解析式,解方程即可.
【详解】解:把代入,得,
解得,,
故选:C.
【点睛】本题考查了反比例函数图象上点的坐标,解题关键是明确反比例函数图象上点的坐标满足函数解析式.
5.C
【分析】直接把点A(3,4)代入反比例函数y=,求出k的值即可.
【详解】解:∵将点A(3,4)代入反比例函数y=,得4=,
解得k=12.
∴反比例函数表达式为:y=,
故选:C.
【点睛】本题考查的是待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
6.B
【分析】将A、B、C三点坐标分别代入反比例函数的解析式,求出的值比较其大小即可
【详解】∵点,,都在反比例函数的图象上,
∴分别把x=-3、x=-2、x=1代入得,,
∴
故选B
【点睛】本题考查了反比例函数的图像和性质,熟练掌握相关的知识点是解题的关键.
7.D
【分析】直接利用反比例函数图象上点的坐标特点进而得出答案.
【详解】解:∵反比例函数y=的图象经过点(3,-2),
∴xy=k=-6,
A、(-3,-2),此时xy=-3×(-2)=6,不合题意;
B、(3,2),此时xy=3×2=6,不合题意;
C、(-2,-3),此时xy=-3×(-2)=6,不合题意;
D、(-2,3),此时xy=-2×3=-6,符合题意;
故选D.
【点睛】此题主要考查了反比例函数图象上点的坐标特征,正确得出k的值是解题关键.
8.B
【详解】解:当为定值时,2与的乘积是定值,所以 2与成反比例.
故选:B.
9.C
【分析】先求出水温开始下降时,水温y()与开机后用时x(min)的反比例函数解析式,再求出水温为35时的时间,计算即可.
【详解】解:设水温开始下降时,水温y()与开机后用时x(min)的反比例解析式为,
代入(7,100)得:,即,
当y=35时,即,
解得:,
∵20-7=13,
∴水温从100降到35所用的时间是13 min,
故选:C.
【点睛】本题考查了求反比例函数解析式,反比例函数图像上点的坐标特征,熟练掌握待定系数法是解题的关键.
10.D
【分析】根据图象中的数据回答即可.
【详解】解:A.海拔越高,大气压越小,该选项不符合题意;
B.∵图象经过点(2,80),(4,60),
∴2×80=160,4×60=240,而160≠240,
∴图中曲线不是反比例函数的图象,该选项不符合题意;
C.∵图象经过点 (4,60),
∴海拔为4千米时,大气压约为60千帕,该选项不符合题意;
D.图中曲线表达了大气压和海拔两个量之间的变化关系,该选项符合题意;
故选:D.
【点睛】本题考查了函数的图象,解题的关键是读懂题意,能正确识图.
11.
【分析】根据反比例函数的定义,即可得到答案.
【详解】解:由题意得:在函数中,,
故答案是:.
【点睛】本题主要考查反比函数自变量取值范围,掌握反比例函数自变量不等于0,是解题的关键.
12.
【分析】设反比例函数解析式为(k≠0),由A点求得k,再由B点横坐标求得纵坐标即可.
【详解】解:设反比例函数解析式为(k≠0),
由点A(2,-6)可得k=xy=-12,
∴,
当x=3时,,
即B(3,-4),
故答案为:-4.
【点睛】本题考查了反比例函数解析式,掌握待定系数法求函数解析式是解题关键.
13.-9
【分析】由点A在反比例函数图象上,可得出ab=-5,将其代入代数式ab-4中即可得出结论.
【详解】解:∵点A(a,b)在反比例函数y=的图象上
∴ab=-5
∴ab-4=-5-4=-9.
故答案为:-9.
【点睛】本题考查了反比例函数图象上点的坐标特征,解题的关键是找出ab=2.本题属于基础题,难度不大,解决该题型题目时,由点在反比例函数图象上可以得出点的横纵坐标之积为定值,将其代入代数式即可.
14.5
【分析】把点的坐标代入函数解析式得出方程,求出方程的解即可.
【详解】解:∵反比例函数的图象经过点(1,2),
∴将(1,2)代入得:k 3=2,
解得:k=5,
故答案为:5.
【点睛】本题考查了反比例函数图象上点的坐标特征,能根据已知得出关于k的方程是解此题的关键.
15.
【分析】将点B的坐标代入反比例函数解析式,得出k的值,再将点A的纵坐标代入即可得出m的值.
【详解】解:将点B的坐标代入反比例函数解析式,得出:,
∴,
将点A的纵坐标代入可得,,解得,.
故答案为:.
【点睛】本题考查的知识点是反比例函数图象上点的坐标,属于基础题目,易于掌握.
16.0
【分析】根据反比例函数的定义,即可求解.
【详解】解:∵函数是反比例函数,
∴且,
解得:m=0.
故答案为:0
【点睛】本题主要考查了反比例函数的定义,解一元二次方程,熟练掌握形如或的形式的函数关系,称为反比例函数是解题的关键.
17.
【分析】根据录入的时间=录入总量÷录入速度即可得出函数关系式.
【详解】解:由录入的时间=录入总量÷录入速度,
可得t(v>0).
故答案为:.
【点睛】本题考查了根据实际问题列函数关系式的知识,比较简单,解答本题的关键是掌握关系式录入的时间=录入总量÷录入速度.
18.8
【分析】由于四边形OABC为平行四边形,根据平移的性质,结合点O、A、B的坐标可确定点C的坐标为(4,2),将其代入带反比例函数解析式求k值即可.
【详解】解:∵四边形OABC为平行四边形,
∴,,
∵A坐标为,点B坐标为,点O坐标为,
由平移的性质可知,点C的坐标为(4,2),
∴将点C(4,2)代入到函数中,
可得,解得.
故答案为:8.
【点睛】本题主要考查了反比例函数图像上点的坐标特征、平行四边形的性质及平移的性质,解题关键是确定C点的坐标.
19.(1)是,;
(2)是,;
(3)否;
(4)是,(可化为);
(5)是,
【分析】利用反比例函数的定义判定即可.
【详解】(1)解:是反比例函数,比例系数;
(2)解:是反比例函数,比例系数;
(3)解:不是反比例函数;
(4)解:∵xy=1,
∴,
∴y是x的反比例函数,比例系数;
(5)解:是反比例函数;比例系数;
【点睛】本题主要考查了反比例函数的定义,解题的关键是熟记反比例函数的定义,反比例函数解析式的一般式y=(k≠0).
20.(1),是反比例函数;(2),是正比例函数,不是反比例函数.
【分析】(1)根据题意列出函数关系式,然后根据反比例函数的定义判断即可;
(2)根据题意列出函数关系式,然后根据正比例函数的定义判断即可;
【详解】(1)由题意,得是反比例函数;
(2)由单价乘以加油量等于总价,得,是正比例函数,不是反比例函数.
【点睛】本题考查了反比例函数与正比例函数的定义,根据题意列出函数关系式是解题关键.
21.(1);(2)
【分析】(1)设,则有,然后把当时,;当时,代入求解即可;
(2)由(1)可直接把x=3代入求解.
【详解】解:(1)设,由可得:,
∴把,和,代入得:
,解得:,
∴y与x的函数解析式为:;
(2)由(1)可把x=3代入得:
.
【点睛】本题主要考查反比例函数的定义及函数解析式,熟练掌握反比例函数的定义及求函数解析式的方法是解题的关键.
22.-3
【分析】由反比例函数的图象及其性质将A、B点代入反比例函数即可求得m的值为-3.
【详解】∵反比例函数的图象经过点,
∴.
∵点在反比例函数的图象上,
∴,
解得:.
故m的轴为-3.
【点睛】本题考查了反比例函数值的求法,明确图象上点的坐标和解析式的关系是解题的关键.
23.(1);(2)见解析
【分析】(1)设反比例函数的表达式为y=,找出函数图象上一个点的坐标,然后代入求解即可;
(2)将x或y的值代入函数解析式求得对应的y或x的值即可.
【详解】解:(1)设反比例函数的表达式为y=,
把代入得,
(2)将y=代入得:;
将代入得:y=;
将代入得:y=9;
将代入得:y=18,
将代入得:x=1;
将x=2代入得:,
将x=3代入得:.
【点睛】本题主要考查的是反比例函数的定义、函数图象上点的坐标与函数解析式之间的关系,求得函数的解析式是解题的关键.
24.点不在反比例函数的图像上,点在反比例函数的图像上
【分析】解分式方程得出的值,将其带入点和点,得出两点的坐标,再验证两点坐标是否在反比例函数上即可得出答案.
【详解】解:由题,解方程
去分母,得,即,解得,
经检验是原分式方程的解,
∴
∵反比例函数,
∴
∵,
∴,
∴点不在反比例函数的图像上,点在反比例函数的图像上.
【点睛】本题考查解分式方程,以及判断坐标系中点是否在反比例函数上,熟练掌握解分式方程的步骤,尤其注意检验是本题解题关键.
答案第1页,共2页
答案第1页,共2页
