2023-2024学年福建省莆田市城厢区重点中学八年级(上)开学数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年福建省莆田市城厢区重点中学八年级(上)开学数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 476.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 11:38:01 | ||
图片预览



文档简介
2023-2024学年福建省莆田市城厢区重点中学八年级(上)开学数学试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1.第届冬季奥林匹克运动会于年月日在世界首个“双奥之城”北京圆满落下帷幕.下列图中所示的四个图案是四届冬季奥林匹克运动会会徽图案上的一部分图形,其中是轴对称图形的是( )
A. B. C. D.
2.若某三角形的三边长分别为,,,则的值可以是( )
A. B. C. D.
3.如图,已知,添加下列条件后不能使≌的是( )
A.
B.
C.
D.
4.如图,( )
A.
B.
C.
D.
5.已知图中的两个三角形全等,则等于( )
A. B. C. D.
6.如图,一棵垂直于地面的树在一次强台风中从高地面米处折断倒下,倒下部分与地面成角,这棵树在折断前的高度为( )
A. 米 B. 米 C. 米 D. 米
7.阅读以下作图步骤:
在和上分别截取,,使;
分别以,为圆心,以大于的长为半径作弧,两弧在内交于点;
作射线,连接,,如图所示.
根据以上作图,一定可以推得的结论是( )
A. 且 B. 且
C. 且 D. 且
8.如图,是等腰底边上的中线,平分,交于点,,,则的面积是( )
A.
B.
C.
D.
9.如图,中,,点,分别在边,上,,,的平分线与的平分线交于点,则的度数是( )
A. B. C. D.
10.如图,点在等边的边上,,射线垂足为点,点是射线上一动点,点是线段上一动点,当的值最小时,,则的长为( )
A. B. C. D.
二、填空题(本大题共6小题,共24.0分)
11.点与关于轴对称, ______ .
12.如图所示,的度数是______ .
13.一个多边形的内角和是外角和的倍,则这个多边形的边数为______.
14.如图,已知,,连接,过点的垂线,使,则点坐标是______.
15.如图,点,在射线上,点,在射线上,且,已知,则 ______ .
16.如图,为线段上一动点不与点、重合,在的上方分别作和,且,,,、交于点有下列结论:;;当时,;平分其中正确的是______把你认为正确结论的序号都填上
三、解答题(本大题共9小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
计算:
18.本小题分
解不等式组:.
19.本小题分
如图,,,求证:.
20.本小题分
如图所示,在中,平分,是的高,,,求的度数.
21.本小题分
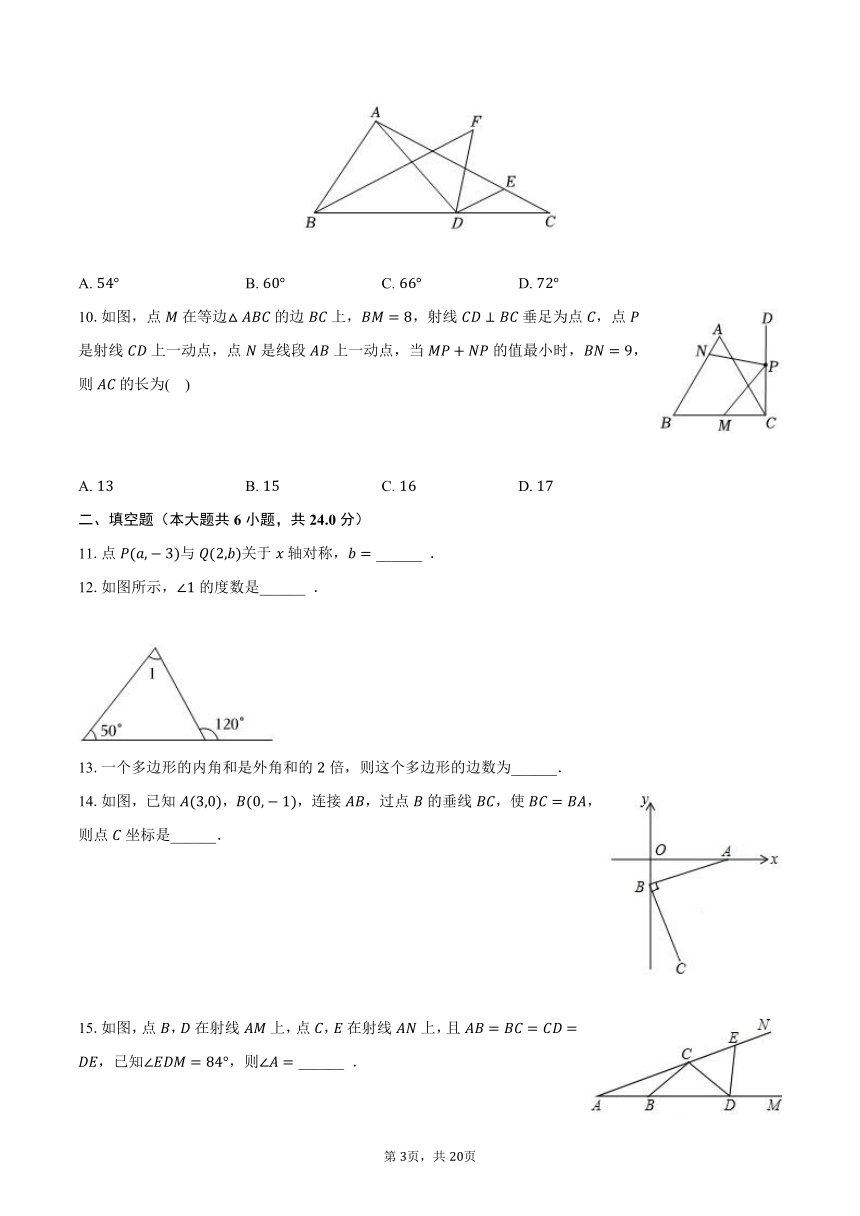
在第六十个学雷锋纪念日到来之际,习近平总书记指出:实践证明,无论时代如何变迁,雷锋精神永不过时,某校为弘扬雷锋精神,组织全校学生开展了手抄报评比活动评比结果共分为四项:非凡创意;魅力色彩;,最美设计:无限潜力参赛的每名学生都恰好获得其中一个奖项,活动结束后,学校数学兴趣小组随机调查了部分学生的获奖情况,将调查结果绘制成如下两幅不完整的统计图.
请根据统计图提供的信息,解答下列问题:
本次共调查了______ 名学生.
请补全条形统计图.
本次评比活动中,全校有名学生参加,根据调查结果,请你估计在评比中获得“非凡创意”奖的学生人数.
22.本小题分
某中,扫码骑共享单车出行可获得绿色能量,能量获取规则:
扫码骑共享单车,开启后单次时长大于等于分钟获得绿色能量; 每分钟可得绿色能量,单次上限分钟,单日上限分钟.
例如:开启后单次时长为分钟,则不能获得能量;若开启后单次时长为分钟,则获得的能量为:.
若小俊在一天中骑了一次共享单车,用了分钟,则小俊这一天从骑共享单车出行可得绿色能量为______ ;
小米在一天中共骑了次共享单车,已知第次和第次骑行的时间分别为分钟和分钟,第次骑行的时间是第次的倍,一共得了的绿色能量,那么小米第次骑行了______ 分钟.
23.本小题分
阅读并完成相应的任务如图,小明站在堤岸凉亭点处,正对他的点与堤岸垂直停有一艘游艇,他想知道凉亭与这艘游艇之间的距离,于是制定了如下方案.
课题 测凉亭与游艇之间的距离
测量工具 皮尺等
测量方案示意图不完整
测量步骤 小明沿堤岸走到电线杆旁直线与堤岸平行;
再往前走相同的距离,到达点;
他到达点后向左转度直行,当自己,电线杆与游艇在一条直线上时停下来,此时小明位于点处.
测量数据 米,米,米
任务一:根据题意将测量方案示意图补充完整;
任务二:
凉亭与游艇之间的距离是______ 米;
请你说明小明方案正确的理由.
24.本小题分
已知如图,为的角平分线,且,为延长线上的一点,.
求证:;
若,,则,之间满足一定的数量关系,请写出这个结论并加以证明.
25.本小题分
如图,在等腰直角中,,,作点关于对称点,连接、、,其中交直线于点,连接设.
设、、的周长分别为、、,求的长;用、、表示
试探究的大小是否会随的改变而改变?如果改变,请用表示其大小;如果不改变,请求出的大小;
若,请求出的值.
答案和解析
1.【答案】
【解析】解:,,选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:.
直接利用轴对称图形的定义进行判断.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
此题主要考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.【答案】
【解析】解:根据三角形的三边关系定理得:,
解得:,
即符合题意的值只有,
故选:.
根据三角形的三边关系定理得出,求出即可.
本题考查了三角形的三边关系定理,能熟记三角形的三边关系定理的内容是解此题的关键.
3.【答案】
【解析】解:,,
若添加,则可以判定≌,故A不符合题意;
若添加,则可以判定≌,故B不符合题意;
若添加,不能判定≌,故C符合题意;
若添加,则可以判定≌,故D不符合题意;
故选:.
根据题目中的条件和全等三角形的判定方法可以判断哪个选项中的说法不能判定≌,从而可以解答本题.
本题考查全等三角形的判定,熟记全等三角形的判定定理是解题的关键.
4.【答案】
【解析】本题主要考查了三角形的内角和外角之间的关系及四边形内角和定理:三角形的外角等于与它不相邻的两个内角和;四边形的内角和为.
根据“三角形的外角等于与它不相邻的两个内角和”可知能把,,,,,全部转化到,所在的四边形中,利用四边形内角和为可得答案.
解:如图,
由图可知,,,
又,
.
故选:.
5.【答案】
【解析】解:图中的两个三角形全等,
.
故选:.
直接利用全等三角形的性质得出对应角进而得出答案.
本题主要考查了全等三角形的性质,正确找出对应角是解题关键.
6.【答案】
【解析】解:,,,
,
这棵树在折断前的高度为米.
故选:.
根据含有角的直角三角形的性质可以得到的长,然后即可计算出的值,从而可以得到这棵树在折断前的高度.
本题考查了含有角的直角三角形的性质,熟练掌握性质是解题的关键.
7.【答案】
【解析】解:、以,为圆心画弧的半径相等,因此,又,,因此≌得到,故A符合题意;
B、因为、的长在变化,所以和不一定相等,因此不一定等于,故B不符合题意;
C、因为、的长在变化,所以和不一定相等,故C不符合题意;
D、的位置在变化,所以和不一定平行,因此不一定等于,故D不符合题意.
故选:.
由≌推出;和不一定相等,因此不一定等于;和不一定相等;和不一定平行,因此不一定等于.
本题考查作图基本作图,全等三角形的判定和性质,关键是由作图得到≌.
8.【答案】
【解析】解:过作于.
是等腰底边上的中线,
,.
平分,,,
.
,,,
.
故选:.
过作于利用角平分线的性质可得到,从而根据三角形面积公式求得的面积.
本题考查角平分线的性质,等腰三角形的性质,解题的关键是掌握角平分线的性质,属于中考常考题型.
9.【答案】
【解析】解:平分,
,
,
,
设,则,
,
,
,
,
平分,
,
,
,
.
故选:.
根据题意可知,设,表示出,根据角平分线的定义,可得的度数,根据列方程,即可求出的度数.
本题考查了三角形的内角和定理,结合图形分析清楚各角之间的关系是解题的关键.
10.【答案】
【解析】解:如图,作点关于直线的对称点,过点作于点,交于点,
,
,
,
由垂线段最短可知,的最小值为,
为等边三角形,
,
,
,
,
,
,
,
,
.
故选:.
作点关于直线的对称点,过点作于点,交于点,由垂线段最短可知的最小值为,再根据含角的直角三角形性质求解即可.
本题主要考查轴对称最短路线问题、等边三角形的性质、含角的直角三角形性质,解题关键是作出其中一点关于直线的对称点,对称点与另一点的连线与直线的交点就是所要找的点.
11.【答案】
【解析】解:点与关于轴对称,
,.
故答案为:.
关于轴对称的点的横坐标相等,纵坐标互为相反数,由此可得答案.
本题考查关于轴、轴对称的点的坐标,熟知:关于轴对称的点的横坐标相等,纵坐标互为相反数;关于轴对称的点的横坐标互为相反数,纵坐标相等.
12.【答案】
【解析】解:,
,
故答案为:.
根据三角形外角的性质可得答案.
本题主要考查三角形外角性质,解题的关键是熟练掌握三角形的一个外角等于和它不相邻的两个内角的和的性质.
13.【答案】
【解析】解:设多边形的边数为,
根据题意得,
解得,
所以这个多边形是六边形.
故答案为:.
本题主要考查了多边形的内角和定理与外角和定理,熟练掌握定理是解题的关键.
利用多边形的外角和以及多边形的内角和定理即可解决问题.
14.【答案】
【解析】解:如图,过点作轴于,
,
,
,
,
,
,
在和中,,
≌,
,,
,,
,,
,,
,
.
过点作轴于,证明≌,得出,,再求出,,即可得出结论;
本题考查了全等三角形的判定和性质,等腰直角三角形的性质,直角三角形的性质等知识;构造出全等三角形是解本题的关键.
15.【答案】
【解析】解:,
,,,
根据三角形的外角性质,,,,
又,
,
解得,,
故答案为:;
根据等边对等角可得,,,再根据三角形的一个外角等于与它不相邻的两个内角的和可得,,,然后用表示出,计算即可求解;
本题考查了等腰三角形两底角相等的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,是基础题.
16.【答案】
【解析】解:,
,即,
在和中,
,
≌,
,故正确;
≌,
,
,
,
,
,
,
,
,
,
,故正确;
,,,
,
,
,
,
,故正确;
如图,连接,过点作于,于,
≌,
,,
,
,
,,
平分,故正确,
故答案为:.
由“”可证≌,可得,可判断;由≌,可得,由,可得,利用三角形内角和定理即可判断;由,,,可得:,进而得出,再运用等腰三角形性质即可判断;由全等三角形的性质可得,由三角形的面积公式可求,由角平分线的性质可得平分,可判断,即可求解.
本题考查了全等三角形的性质定理和判定,等腰三角形的判定和性质,三角形内角和定理,三角形面积,角平分线的判定等,熟练掌握全等三角形的判定和性质是解此题的关键.
17.【答案】解:原式
.
【解析】先化成最简二次根式,再根据二次根式的加减法则求出即可.
本题考查了二次根式的加减,能灵活运用法则进行计算是解此题的关键.
18.【答案】解:,
解不等式,得:,
解不等式,得:,
原不等式组的解集是.
【解析】先解出每个不等式的解集,即可得到不等式组的解集.
本题考查解一元一次不等式组,解答本题的关键是明确解一元一次不等式的方法.
19.【答案】证明:,
,
即.
在和中,
,
≌,
.
【解析】根据角的和差求得,根据全等三角形的判定和性质定理即可得到结论.
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定和性质定理是解题的关键.
20.【答案】解:平分,,
,
,
,
是的高,
,
.
【解析】根据角平分线的定义求出,根据三角形内角和求出,利用高线的定义得到,再用三角形内角和求出结果.
本题考查了三角形内角和定理,角平分线的定义,三角形的高,熟记定理并准确识图,观察出是解题的关键.
21.【答案】
【解析】解:名,
故答案为:;
样本中获得“魅力色彩”的人数为:名,
补全条形统计图如下:
人,
答:全校有名学生中获得“非凡创意”奖的学生大约有人.
从两个统计图可知,样本中获得“无限潜力”的有人,占调查人数的,由频率可求出调查人数;
求出样本中获得“魅力色彩”的人数即可补全条形统计图;
求出样本中获得“非凡创意”奖的学生所占的百分比,估计总体中获得“非凡创意”奖的学生所占的百分比,进而求出相应的人数.
本题考查条形统计图、扇形统计图以及样本估计总体,掌握频率是正确解答的关键.
22.【答案】
【解析】解:小俊这一天从骑共享单车出行可得绿色能量为:;
故答案为:;
设小米第次骑行了分钟,第次骑行了分钟,根据题意得:
,
解得:,
,
第次骑行时间大于分钟,
第次实际骑行时间为:分钟,
第次实际骑行时间为:分钟,
故答案为:.
根据每分钟可得绿色能量,求出分钟获得的绿色能量即可;
设小米第次骑行了分钟,第次骑行了分钟,列方程求出第次实际骑行时间,即可求出第次实际骑行时间.
本题主要考查了一元一次方程的应用,解题的关键是理解题意,找出题目中的等量关系,列出方程,准确计算.
23.【答案】
【解析】解:任务一:将测量方案示意图补充完整如图所示.
任务二:由≌得米,
故答案为:.
理由:如图,
由题意可知,米,米,米,,,
,,
在和中,
,
≌,
米,
小明的方案是正确的.
任务一:根据题意可知,小华的方案中蕴含着一对全等三角形,即≌,将图形补充完整即可;
任务二:由补充完整的图形可知,≌,且与是对应边,可知米,得出答案为;
由题意可知米,,与是对顶角,由“”可判定≌,则米,说明小明的方案是正确的.
此题考查全等三角形的判定与性质、全等三角形的应用等知识与方法,解题的关键是从实际问题中抽象出全等三角形的图形.
24.【答案】证明:为的角平分线,
,
在和中,
,
≌,
;
解:,
,
为的角平分线,
,
由知≌,
,
,
,
,
,
,
,
.
【解析】由证明≌,根据全等三角形的性质即可得出;
根据等腰三角形的性质可得,由角平分线的定义得,再根据全等三角形的性质和三角形的内角和得,由和三角形的内角和即可得出结论.
本题考查了全等三角形的判定与性质、等腰三角形的性质与判定、三角形内角和定理等知识,证明三角形全等是解决问题的关键.
25.【答案】解:点、点关于对称,
,
,,,
,,,
,
;
,是个定值,理由如下:
点、点关于对称,
,,
,,
,
又,
,
,
.
如图,作,垂足为由可知,,
,
,
点、点关于对称,
,
,
,
,
.
【解析】分别写出三个三角形的周长,能够发现大三角形的周长与两个小三角形周长和的关系,即可转化成求的代数式;
利用对称性得到,根据八字模型得到,可知是等腰直角三角形即可;
作,垂足为由可知,,,利用对称得到,继而,代入数据计算即可.
本题考查了轴对称的性质和等腰直角三角形的性质,熟悉特殊三角形的边角关系是解本题的关键.
第1页,共1页
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1.第届冬季奥林匹克运动会于年月日在世界首个“双奥之城”北京圆满落下帷幕.下列图中所示的四个图案是四届冬季奥林匹克运动会会徽图案上的一部分图形,其中是轴对称图形的是( )
A. B. C. D.
2.若某三角形的三边长分别为,,,则的值可以是( )
A. B. C. D.
3.如图,已知,添加下列条件后不能使≌的是( )
A.
B.
C.
D.
4.如图,( )
A.
B.
C.
D.
5.已知图中的两个三角形全等,则等于( )
A. B. C. D.
6.如图,一棵垂直于地面的树在一次强台风中从高地面米处折断倒下,倒下部分与地面成角,这棵树在折断前的高度为( )
A. 米 B. 米 C. 米 D. 米
7.阅读以下作图步骤:
在和上分别截取,,使;
分别以,为圆心,以大于的长为半径作弧,两弧在内交于点;
作射线,连接,,如图所示.
根据以上作图,一定可以推得的结论是( )
A. 且 B. 且
C. 且 D. 且
8.如图,是等腰底边上的中线,平分,交于点,,,则的面积是( )
A.
B.
C.
D.
9.如图,中,,点,分别在边,上,,,的平分线与的平分线交于点,则的度数是( )
A. B. C. D.
10.如图,点在等边的边上,,射线垂足为点,点是射线上一动点,点是线段上一动点,当的值最小时,,则的长为( )
A. B. C. D.
二、填空题(本大题共6小题,共24.0分)
11.点与关于轴对称, ______ .
12.如图所示,的度数是______ .
13.一个多边形的内角和是外角和的倍,则这个多边形的边数为______.
14.如图,已知,,连接,过点的垂线,使,则点坐标是______.
15.如图,点,在射线上,点,在射线上,且,已知,则 ______ .
16.如图,为线段上一动点不与点、重合,在的上方分别作和,且,,,、交于点有下列结论:;;当时,;平分其中正确的是______把你认为正确结论的序号都填上
三、解答题(本大题共9小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
计算:
18.本小题分
解不等式组:.
19.本小题分
如图,,,求证:.
20.本小题分
如图所示,在中,平分,是的高,,,求的度数.
21.本小题分
在第六十个学雷锋纪念日到来之际,习近平总书记指出:实践证明,无论时代如何变迁,雷锋精神永不过时,某校为弘扬雷锋精神,组织全校学生开展了手抄报评比活动评比结果共分为四项:非凡创意;魅力色彩;,最美设计:无限潜力参赛的每名学生都恰好获得其中一个奖项,活动结束后,学校数学兴趣小组随机调查了部分学生的获奖情况,将调查结果绘制成如下两幅不完整的统计图.
请根据统计图提供的信息,解答下列问题:
本次共调查了______ 名学生.
请补全条形统计图.
本次评比活动中,全校有名学生参加,根据调查结果,请你估计在评比中获得“非凡创意”奖的学生人数.
22.本小题分
某中,扫码骑共享单车出行可获得绿色能量,能量获取规则:
扫码骑共享单车,开启后单次时长大于等于分钟获得绿色能量; 每分钟可得绿色能量,单次上限分钟,单日上限分钟.
例如:开启后单次时长为分钟,则不能获得能量;若开启后单次时长为分钟,则获得的能量为:.
若小俊在一天中骑了一次共享单车,用了分钟,则小俊这一天从骑共享单车出行可得绿色能量为______ ;
小米在一天中共骑了次共享单车,已知第次和第次骑行的时间分别为分钟和分钟,第次骑行的时间是第次的倍,一共得了的绿色能量,那么小米第次骑行了______ 分钟.
23.本小题分
阅读并完成相应的任务如图,小明站在堤岸凉亭点处,正对他的点与堤岸垂直停有一艘游艇,他想知道凉亭与这艘游艇之间的距离,于是制定了如下方案.
课题 测凉亭与游艇之间的距离
测量工具 皮尺等
测量方案示意图不完整
测量步骤 小明沿堤岸走到电线杆旁直线与堤岸平行;
再往前走相同的距离,到达点;
他到达点后向左转度直行,当自己,电线杆与游艇在一条直线上时停下来,此时小明位于点处.
测量数据 米,米,米
任务一:根据题意将测量方案示意图补充完整;
任务二:
凉亭与游艇之间的距离是______ 米;
请你说明小明方案正确的理由.
24.本小题分
已知如图,为的角平分线,且,为延长线上的一点,.
求证:;
若,,则,之间满足一定的数量关系,请写出这个结论并加以证明.
25.本小题分
如图,在等腰直角中,,,作点关于对称点,连接、、,其中交直线于点,连接设.
设、、的周长分别为、、,求的长;用、、表示
试探究的大小是否会随的改变而改变?如果改变,请用表示其大小;如果不改变,请求出的大小;
若,请求出的值.
答案和解析
1.【答案】
【解析】解:,,选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:.
直接利用轴对称图形的定义进行判断.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
此题主要考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.【答案】
【解析】解:根据三角形的三边关系定理得:,
解得:,
即符合题意的值只有,
故选:.
根据三角形的三边关系定理得出,求出即可.
本题考查了三角形的三边关系定理,能熟记三角形的三边关系定理的内容是解此题的关键.
3.【答案】
【解析】解:,,
若添加,则可以判定≌,故A不符合题意;
若添加,则可以判定≌,故B不符合题意;
若添加,不能判定≌,故C符合题意;
若添加,则可以判定≌,故D不符合题意;
故选:.
根据题目中的条件和全等三角形的判定方法可以判断哪个选项中的说法不能判定≌,从而可以解答本题.
本题考查全等三角形的判定,熟记全等三角形的判定定理是解题的关键.
4.【答案】
【解析】本题主要考查了三角形的内角和外角之间的关系及四边形内角和定理:三角形的外角等于与它不相邻的两个内角和;四边形的内角和为.
根据“三角形的外角等于与它不相邻的两个内角和”可知能把,,,,,全部转化到,所在的四边形中,利用四边形内角和为可得答案.
解:如图,
由图可知,,,
又,
.
故选:.
5.【答案】
【解析】解:图中的两个三角形全等,
.
故选:.
直接利用全等三角形的性质得出对应角进而得出答案.
本题主要考查了全等三角形的性质,正确找出对应角是解题关键.
6.【答案】
【解析】解:,,,
,
这棵树在折断前的高度为米.
故选:.
根据含有角的直角三角形的性质可以得到的长,然后即可计算出的值,从而可以得到这棵树在折断前的高度.
本题考查了含有角的直角三角形的性质,熟练掌握性质是解题的关键.
7.【答案】
【解析】解:、以,为圆心画弧的半径相等,因此,又,,因此≌得到,故A符合题意;
B、因为、的长在变化,所以和不一定相等,因此不一定等于,故B不符合题意;
C、因为、的长在变化,所以和不一定相等,故C不符合题意;
D、的位置在变化,所以和不一定平行,因此不一定等于,故D不符合题意.
故选:.
由≌推出;和不一定相等,因此不一定等于;和不一定相等;和不一定平行,因此不一定等于.
本题考查作图基本作图,全等三角形的判定和性质,关键是由作图得到≌.
8.【答案】
【解析】解:过作于.
是等腰底边上的中线,
,.
平分,,,
.
,,,
.
故选:.
过作于利用角平分线的性质可得到,从而根据三角形面积公式求得的面积.
本题考查角平分线的性质,等腰三角形的性质,解题的关键是掌握角平分线的性质,属于中考常考题型.
9.【答案】
【解析】解:平分,
,
,
,
设,则,
,
,
,
,
平分,
,
,
,
.
故选:.
根据题意可知,设,表示出,根据角平分线的定义,可得的度数,根据列方程,即可求出的度数.
本题考查了三角形的内角和定理,结合图形分析清楚各角之间的关系是解题的关键.
10.【答案】
【解析】解:如图,作点关于直线的对称点,过点作于点,交于点,
,
,
,
由垂线段最短可知,的最小值为,
为等边三角形,
,
,
,
,
,
,
,
,
.
故选:.
作点关于直线的对称点,过点作于点,交于点,由垂线段最短可知的最小值为,再根据含角的直角三角形性质求解即可.
本题主要考查轴对称最短路线问题、等边三角形的性质、含角的直角三角形性质,解题关键是作出其中一点关于直线的对称点,对称点与另一点的连线与直线的交点就是所要找的点.
11.【答案】
【解析】解:点与关于轴对称,
,.
故答案为:.
关于轴对称的点的横坐标相等,纵坐标互为相反数,由此可得答案.
本题考查关于轴、轴对称的点的坐标,熟知:关于轴对称的点的横坐标相等,纵坐标互为相反数;关于轴对称的点的横坐标互为相反数,纵坐标相等.
12.【答案】
【解析】解:,
,
故答案为:.
根据三角形外角的性质可得答案.
本题主要考查三角形外角性质,解题的关键是熟练掌握三角形的一个外角等于和它不相邻的两个内角的和的性质.
13.【答案】
【解析】解:设多边形的边数为,
根据题意得,
解得,
所以这个多边形是六边形.
故答案为:.
本题主要考查了多边形的内角和定理与外角和定理,熟练掌握定理是解题的关键.
利用多边形的外角和以及多边形的内角和定理即可解决问题.
14.【答案】
【解析】解:如图,过点作轴于,
,
,
,
,
,
,
在和中,,
≌,
,,
,,
,,
,,
,
.
过点作轴于,证明≌,得出,,再求出,,即可得出结论;
本题考查了全等三角形的判定和性质,等腰直角三角形的性质,直角三角形的性质等知识;构造出全等三角形是解本题的关键.
15.【答案】
【解析】解:,
,,,
根据三角形的外角性质,,,,
又,
,
解得,,
故答案为:;
根据等边对等角可得,,,再根据三角形的一个外角等于与它不相邻的两个内角的和可得,,,然后用表示出,计算即可求解;
本题考查了等腰三角形两底角相等的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,是基础题.
16.【答案】
【解析】解:,
,即,
在和中,
,
≌,
,故正确;
≌,
,
,
,
,
,
,
,
,
,
,故正确;
,,,
,
,
,
,
,故正确;
如图,连接,过点作于,于,
≌,
,,
,
,
,,
平分,故正确,
故答案为:.
由“”可证≌,可得,可判断;由≌,可得,由,可得,利用三角形内角和定理即可判断;由,,,可得:,进而得出,再运用等腰三角形性质即可判断;由全等三角形的性质可得,由三角形的面积公式可求,由角平分线的性质可得平分,可判断,即可求解.
本题考查了全等三角形的性质定理和判定,等腰三角形的判定和性质,三角形内角和定理,三角形面积,角平分线的判定等,熟练掌握全等三角形的判定和性质是解此题的关键.
17.【答案】解:原式
.
【解析】先化成最简二次根式,再根据二次根式的加减法则求出即可.
本题考查了二次根式的加减,能灵活运用法则进行计算是解此题的关键.
18.【答案】解:,
解不等式,得:,
解不等式,得:,
原不等式组的解集是.
【解析】先解出每个不等式的解集,即可得到不等式组的解集.
本题考查解一元一次不等式组,解答本题的关键是明确解一元一次不等式的方法.
19.【答案】证明:,
,
即.
在和中,
,
≌,
.
【解析】根据角的和差求得,根据全等三角形的判定和性质定理即可得到结论.
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定和性质定理是解题的关键.
20.【答案】解:平分,,
,
,
,
是的高,
,
.
【解析】根据角平分线的定义求出,根据三角形内角和求出,利用高线的定义得到,再用三角形内角和求出结果.
本题考查了三角形内角和定理,角平分线的定义,三角形的高,熟记定理并准确识图,观察出是解题的关键.
21.【答案】
【解析】解:名,
故答案为:;
样本中获得“魅力色彩”的人数为:名,
补全条形统计图如下:
人,
答:全校有名学生中获得“非凡创意”奖的学生大约有人.
从两个统计图可知,样本中获得“无限潜力”的有人,占调查人数的,由频率可求出调查人数;
求出样本中获得“魅力色彩”的人数即可补全条形统计图;
求出样本中获得“非凡创意”奖的学生所占的百分比,估计总体中获得“非凡创意”奖的学生所占的百分比,进而求出相应的人数.
本题考查条形统计图、扇形统计图以及样本估计总体,掌握频率是正确解答的关键.
22.【答案】
【解析】解:小俊这一天从骑共享单车出行可得绿色能量为:;
故答案为:;
设小米第次骑行了分钟,第次骑行了分钟,根据题意得:
,
解得:,
,
第次骑行时间大于分钟,
第次实际骑行时间为:分钟,
第次实际骑行时间为:分钟,
故答案为:.
根据每分钟可得绿色能量,求出分钟获得的绿色能量即可;
设小米第次骑行了分钟,第次骑行了分钟,列方程求出第次实际骑行时间,即可求出第次实际骑行时间.
本题主要考查了一元一次方程的应用,解题的关键是理解题意,找出题目中的等量关系,列出方程,准确计算.
23.【答案】
【解析】解:任务一:将测量方案示意图补充完整如图所示.
任务二:由≌得米,
故答案为:.
理由:如图,
由题意可知,米,米,米,,,
,,
在和中,
,
≌,
米,
小明的方案是正确的.
任务一:根据题意可知,小华的方案中蕴含着一对全等三角形,即≌,将图形补充完整即可;
任务二:由补充完整的图形可知,≌,且与是对应边,可知米,得出答案为;
由题意可知米,,与是对顶角,由“”可判定≌,则米,说明小明的方案是正确的.
此题考查全等三角形的判定与性质、全等三角形的应用等知识与方法,解题的关键是从实际问题中抽象出全等三角形的图形.
24.【答案】证明:为的角平分线,
,
在和中,
,
≌,
;
解:,
,
为的角平分线,
,
由知≌,
,
,
,
,
,
,
,
.
【解析】由证明≌,根据全等三角形的性质即可得出;
根据等腰三角形的性质可得,由角平分线的定义得,再根据全等三角形的性质和三角形的内角和得,由和三角形的内角和即可得出结论.
本题考查了全等三角形的判定与性质、等腰三角形的性质与判定、三角形内角和定理等知识,证明三角形全等是解决问题的关键.
25.【答案】解:点、点关于对称,
,
,,,
,,,
,
;
,是个定值,理由如下:
点、点关于对称,
,,
,,
,
又,
,
,
.
如图,作,垂足为由可知,,
,
,
点、点关于对称,
,
,
,
,
.
【解析】分别写出三个三角形的周长,能够发现大三角形的周长与两个小三角形周长和的关系,即可转化成求的代数式;
利用对称性得到,根据八字模型得到,可知是等腰直角三角形即可;
作,垂足为由可知,,,利用对称得到,继而,代入数据计算即可.
本题考查了轴对称的性质和等腰直角三角形的性质,熟悉特殊三角形的边角关系是解本题的关键.
第1页,共1页
同课章节目录
