人教版八年级数学上册试题 第十一章 三角形单元测试卷(含答案)
文档属性
| 名称 | 人教版八年级数学上册试题 第十一章 三角形单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 601.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 15:00:38 | ||
图片预览



文档简介
第十一章 三角形单元测试卷
一、选择题(每题3分,共24分)
1.下列长度的三条线段能组成三角形的是 ( )
A.6,5,10 B.5,3,2 C.5,8,14 D.6,9,2
2.在中,,,则的度数是 ( )
A.40° B.60° C.80° D.160°
3.一个三角形的两个内角的度数分别是42°和73°,这个三角形是 ( )
A.直角三角形 B.锐角三角形
C.全等三角形 D.钝角三角形
4.已知:如图,在中,是的平分线,E为上一点,且于点F.若,,则∠B的度数为 ( )
A.60° B.65° C.75° D.85°
5.如图,求 ( )
A. B. C. D.
6.三角形的下列线段中,能将三角形的面积分成相等两部分的是 ( )
A.中线 B.角平分线 C.高 D.以上都不对
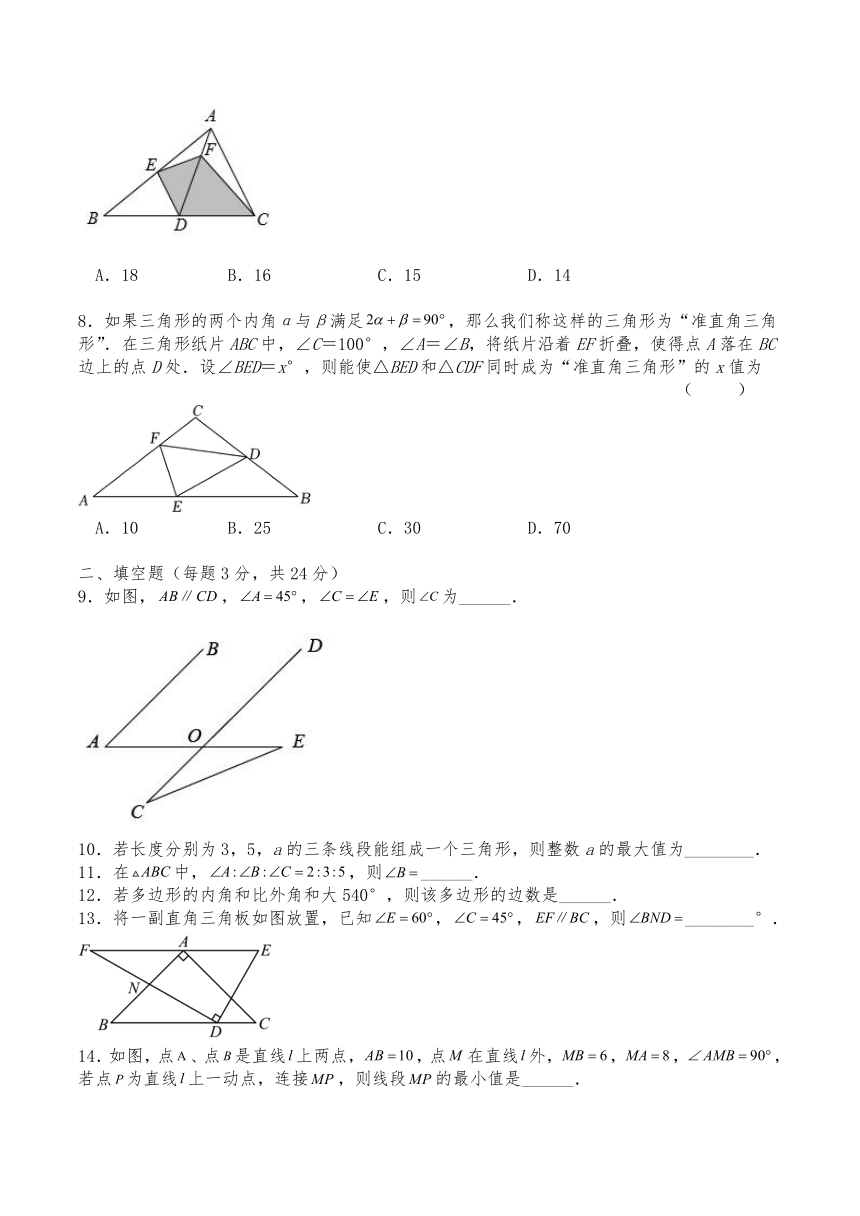
7.如图,D、E分别是ABC边BC、AB边上的中点,F是AD上一点且,若阴影部分的面积为9,则ABC的面积是 ( )
A.18 B.16 C.15 D.14
8.如果三角形的两个内角α与β满足,那么我们称这样的三角形为“准直角三角形”.在三角形纸片ABC中,∠C=100°,∠A=∠B,将纸片沿着EF折叠,使得点A落在BC边上的点D处.设∠BED=x°,则能使△BED和△CDF同时成为“准直角三角形”的x值为
( )
A.10 B.25 C.30 D.70
二、填空题(每题3分,共24分)
9.如图,,,,则为______.
10.若长度分别为3,5,a的三条线段能组成一个三角形,则整数a的最大值为________.
11.在中,,则______.
12.若多边形的内角和比外角和大540°,则该多边形的边数是______.
13.将一副直角三角板如图放置,已知,,,则________°.
14.如图,点、点是直线上两点,,点在直线外,,,,若点为直线上一动点,连接,则线段的最小值是______.
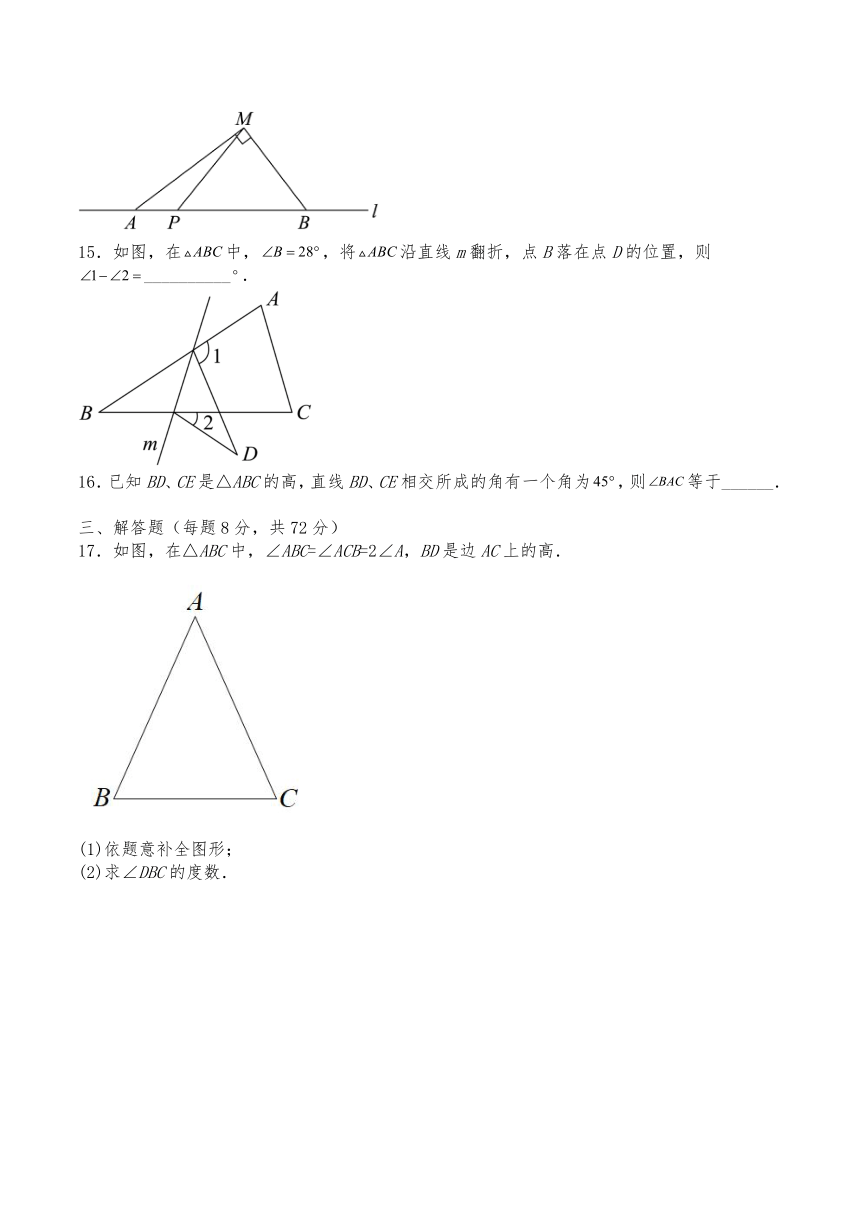
15.如图,在中,,将沿直线m翻折,点B落在点D的位置,则__________.
16.已知BD、CE是△ABC的高,直线BD、CE相交所成的角有一个角为,则等于______.
三、解答题(每题8分,共72分)
17.如图,在△ABC中,∠ABC=∠ACB=2∠A,BD是边AC上的高.
(1)依题意补全图形;
(2)求∠DBC的度数.
18.如图,AD、BE分别是的高和角平分线,,求的度数.
19.一个多边形,它的内角和比外角和的4倍多1800,求这个多边形的边数及内角和度数.
20.如图,E,G分别是AB,AC上的点,F,D是BC上的点,连接EF,AD,DG,已知,.
(1)求证:;
(2)若DG是∠ADC的平分线,,求∠B的度数.
21.已知:如图,AD是△ABC的角平分线,DE∥AC,DE交AB于点E,DF∥AB,DF交AC于点F.求证:DA平分∠EDF.
22.如图,AD、AF分别为的中线、高,点E为AD的中点.
(1)若,,求的度数;
(2)若的面积为15,,求AF的长.
23.如图,在△ABC中,D为AB边上一点,E为BC边上一点,∠BCD=∠BDC
(1)若∠ACD=15°,∠CAD=40°,则∠B= 度(直接写出答案);
(2)请说明:∠EAB+∠AEB=2∠BDC的理由.
24.在四边形ABCD中,∠A=100°,∠D=140°.
(1)如图①,若∠B=∠C,则∠B= 度;
(2)如图②,作∠BCD的平分线CE交AB于点E.若CE∥AD,求∠B的大小.
25.直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有两个角度数的比是3:2,请直接写出∠ABO的度数 .
答案
一、选择题
A.C.B.B.D.A.A.A.
二、填空题
9..
10.7.
11.54°
12.七.
13.105
14..
15..
16.45°或135°.
三、解答题
17.
(1)如图,为边上的高
(2)在△ABC中,∠A+∠ABC+∠ACB=180°
∵∠ABC=∠ACB=2∠A
∴5∠A=180°
∴ ∠A=36°
∴ ∠ABC=∠ACB=72°
在△BCD中,∵BD⊥AC
∴∠BDC=90°
∴ ∠ACB+∠DBC=90°
∵∠ACB=72°
∴∠DBC=18°
18.
解:∵AD、BE分别是的高和角平分线,
∴∠ADB=∠ADC=90°,,
又∵,
∴∠ABC=180°-∠ADB-∠BAD=64°,∠CAD=180°-∠C-∠ADC=60°,
∴,
∴,
∴的度数为62°.
19.
解:根据题意,得
(n 2) 180°=360°×4+180°,
解得:n=11.
360°×4+180°=1620°
则这个多边形的边数是11,内角和度数是1620度.
20.
(1)证明:∵,
∴.
又∵,.
∴.
(2)∵,,
∴.
又∵DG是∠ADC的平分线,
∴.
∵,
∴.
21.
解:∵DE∥AC,
∴∠ADE=∠DAF,
∵DF∥AB,
∴∠ADF=∠DAE,
又∵AD是△ABC的角平分线,
∴∠DAE=∠DAF,
∴∠ADE=∠ADF.
DA平分∠EDF.
22.
(1),,
;
(2)BE为三角形ABD中线,,
,
∵AF⊥BC,BD=5,
,
.
23.
(1)解:∵∠ACD=15°,∠CAD=40°,
∴∠BDC=∠ACD+∠CAD=55°,
∴∠BCD=∠BDC=55°.
在△BCD中,∠BDC+∠BCD+∠B=180°,
∴∠B=180°﹣55°﹣55°=70°.
故答案为:70;
(2)解:在△ABE中,∠EAB+∠AEB+∠B=180°,
∴∠EAB+∠AEB=180°﹣∠B.
在△BCD中,∠BDC+∠BCD+∠B=180°,∠BCD=∠BDC,
∴2∠BDC=180°﹣∠B,
∴∠EAB+∠AEB=2∠BDC.
24.
(1)∵∠A=100°,∠D=140°,
∴∠B=∠C==60°,
故答案为60;
(2)∵CE//AD,
∴∠DCE+∠D=180°,
∴∠DCE=40°,
∵CE平分∠BCD,
∴∠BCD=80°,
∴∠B=360°﹣(100°+140°+80°)=40°.
25.
(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=∠OAB,∠ABE=∠ABO,
∴∠BAE+∠ABE= (∠OAB+∠ABO)=45°,
∴∠AEB=135°;
(2)∠CED的大小不变.
如图,延长AD、BC交于点F.
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=∠BAP,∠ABC=∠ABM,
∴∠BAD+∠ABC= (∠PAB+∠ABM)=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,
∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠CED=67.5°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=∠BAO,∠EOQ=∠BOQ,
∴∠E=∠EOQ ∠EAO= (∠BOQ ∠BAO)= ∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.
在△AEF中,
∵有两个角度数的比是3:2,故有:
∠EAF:∠E=3:2,∠E=60°,∠ABO=120°(舍去);
∠EAF:∠F=3:2,∠E=30°,∠ABO=60°;
∠F:∠E=3:2,∠E=36°,∠ABO=72°;
∠E:∠F=3:2,∠E=54°,∠ABO=108°(舍去).
∴∠ABO为60°或72°.
故答案为:60°或72°.
一、选择题(每题3分,共24分)
1.下列长度的三条线段能组成三角形的是 ( )
A.6,5,10 B.5,3,2 C.5,8,14 D.6,9,2
2.在中,,,则的度数是 ( )
A.40° B.60° C.80° D.160°
3.一个三角形的两个内角的度数分别是42°和73°,这个三角形是 ( )
A.直角三角形 B.锐角三角形
C.全等三角形 D.钝角三角形
4.已知:如图,在中,是的平分线,E为上一点,且于点F.若,,则∠B的度数为 ( )
A.60° B.65° C.75° D.85°
5.如图,求 ( )
A. B. C. D.
6.三角形的下列线段中,能将三角形的面积分成相等两部分的是 ( )
A.中线 B.角平分线 C.高 D.以上都不对
7.如图,D、E分别是ABC边BC、AB边上的中点,F是AD上一点且,若阴影部分的面积为9,则ABC的面积是 ( )
A.18 B.16 C.15 D.14
8.如果三角形的两个内角α与β满足,那么我们称这样的三角形为“准直角三角形”.在三角形纸片ABC中,∠C=100°,∠A=∠B,将纸片沿着EF折叠,使得点A落在BC边上的点D处.设∠BED=x°,则能使△BED和△CDF同时成为“准直角三角形”的x值为
( )
A.10 B.25 C.30 D.70
二、填空题(每题3分,共24分)
9.如图,,,,则为______.
10.若长度分别为3,5,a的三条线段能组成一个三角形,则整数a的最大值为________.
11.在中,,则______.
12.若多边形的内角和比外角和大540°,则该多边形的边数是______.
13.将一副直角三角板如图放置,已知,,,则________°.
14.如图,点、点是直线上两点,,点在直线外,,,,若点为直线上一动点,连接,则线段的最小值是______.
15.如图,在中,,将沿直线m翻折,点B落在点D的位置,则__________.
16.已知BD、CE是△ABC的高,直线BD、CE相交所成的角有一个角为,则等于______.
三、解答题(每题8分,共72分)
17.如图,在△ABC中,∠ABC=∠ACB=2∠A,BD是边AC上的高.
(1)依题意补全图形;
(2)求∠DBC的度数.
18.如图,AD、BE分别是的高和角平分线,,求的度数.
19.一个多边形,它的内角和比外角和的4倍多1800,求这个多边形的边数及内角和度数.
20.如图,E,G分别是AB,AC上的点,F,D是BC上的点,连接EF,AD,DG,已知,.
(1)求证:;
(2)若DG是∠ADC的平分线,,求∠B的度数.
21.已知:如图,AD是△ABC的角平分线,DE∥AC,DE交AB于点E,DF∥AB,DF交AC于点F.求证:DA平分∠EDF.
22.如图,AD、AF分别为的中线、高,点E为AD的中点.
(1)若,,求的度数;
(2)若的面积为15,,求AF的长.
23.如图,在△ABC中,D为AB边上一点,E为BC边上一点,∠BCD=∠BDC
(1)若∠ACD=15°,∠CAD=40°,则∠B= 度(直接写出答案);
(2)请说明:∠EAB+∠AEB=2∠BDC的理由.
24.在四边形ABCD中,∠A=100°,∠D=140°.
(1)如图①,若∠B=∠C,则∠B= 度;
(2)如图②,作∠BCD的平分线CE交AB于点E.若CE∥AD,求∠B的大小.
25.直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有两个角度数的比是3:2,请直接写出∠ABO的度数 .
答案
一、选择题
A.C.B.B.D.A.A.A.
二、填空题
9..
10.7.
11.54°
12.七.
13.105
14..
15..
16.45°或135°.
三、解答题
17.
(1)如图,为边上的高
(2)在△ABC中,∠A+∠ABC+∠ACB=180°
∵∠ABC=∠ACB=2∠A
∴5∠A=180°
∴ ∠A=36°
∴ ∠ABC=∠ACB=72°
在△BCD中,∵BD⊥AC
∴∠BDC=90°
∴ ∠ACB+∠DBC=90°
∵∠ACB=72°
∴∠DBC=18°
18.
解:∵AD、BE分别是的高和角平分线,
∴∠ADB=∠ADC=90°,,
又∵,
∴∠ABC=180°-∠ADB-∠BAD=64°,∠CAD=180°-∠C-∠ADC=60°,
∴,
∴,
∴的度数为62°.
19.
解:根据题意,得
(n 2) 180°=360°×4+180°,
解得:n=11.
360°×4+180°=1620°
则这个多边形的边数是11,内角和度数是1620度.
20.
(1)证明:∵,
∴.
又∵,.
∴.
(2)∵,,
∴.
又∵DG是∠ADC的平分线,
∴.
∵,
∴.
21.
解:∵DE∥AC,
∴∠ADE=∠DAF,
∵DF∥AB,
∴∠ADF=∠DAE,
又∵AD是△ABC的角平分线,
∴∠DAE=∠DAF,
∴∠ADE=∠ADF.
DA平分∠EDF.
22.
(1),,
;
(2)BE为三角形ABD中线,,
,
∵AF⊥BC,BD=5,
,
.
23.
(1)解:∵∠ACD=15°,∠CAD=40°,
∴∠BDC=∠ACD+∠CAD=55°,
∴∠BCD=∠BDC=55°.
在△BCD中,∠BDC+∠BCD+∠B=180°,
∴∠B=180°﹣55°﹣55°=70°.
故答案为:70;
(2)解:在△ABE中,∠EAB+∠AEB+∠B=180°,
∴∠EAB+∠AEB=180°﹣∠B.
在△BCD中,∠BDC+∠BCD+∠B=180°,∠BCD=∠BDC,
∴2∠BDC=180°﹣∠B,
∴∠EAB+∠AEB=2∠BDC.
24.
(1)∵∠A=100°,∠D=140°,
∴∠B=∠C==60°,
故答案为60;
(2)∵CE//AD,
∴∠DCE+∠D=180°,
∴∠DCE=40°,
∵CE平分∠BCD,
∴∠BCD=80°,
∴∠B=360°﹣(100°+140°+80°)=40°.
25.
(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=∠OAB,∠ABE=∠ABO,
∴∠BAE+∠ABE= (∠OAB+∠ABO)=45°,
∴∠AEB=135°;
(2)∠CED的大小不变.
如图,延长AD、BC交于点F.
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=∠BAP,∠ABC=∠ABM,
∴∠BAD+∠ABC= (∠PAB+∠ABM)=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,
∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠CED=67.5°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=∠BAO,∠EOQ=∠BOQ,
∴∠E=∠EOQ ∠EAO= (∠BOQ ∠BAO)= ∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.
在△AEF中,
∵有两个角度数的比是3:2,故有:
∠EAF:∠E=3:2,∠E=60°,∠ABO=120°(舍去);
∠EAF:∠F=3:2,∠E=30°,∠ABO=60°;
∠F:∠E=3:2,∠E=36°,∠ABO=72°;
∠E:∠F=3:2,∠E=54°,∠ABO=108°(舍去).
∴∠ABO为60°或72°.
故答案为:60°或72°.
