安徽省合肥市庐江县2023-2024学年九年级上学期月考数学试题(含解析)
文档属性
| 名称 | 安徽省合肥市庐江县2023-2024学年九年级上学期月考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 16:04:54 | ||
图片预览


文档简介
2024届第一学期10月份阶段练习
九年级数学
注意事项:
1.数学练习满分150分,练习时间为120分钟.
2.本练习包括“练习卷”(共6页)和“答题卷”(共6页)两部分.
3.请务必在“答题卷”上答题,在“练习卷”上答题无效.
4.练习结束时,请将“练习卷”和“答题卷”一并交回.
一、选择题(本题共10小题,每小题4分,满分40分)
1.将一元二次方程2x2-3x=1化成一般形式后,它的二次项系数、一次项系数和常数项分别为( )
A.2,-3,-1 B.2,-3,1 C.-2,3,-1 D.-2,-3,1
2.下列函数解析式中,y一定是x的二次函数的是( )
A.y=x2-+1 B. y=2x2 C.y=(m-3)x2+x-1 D.y=ax2+bx+c
3.若关于x的一元二次方程x2-ax+6=0的一个根是2,则a的值为( )
A.2 B.3 C.4 D.5
4.如果关于x的一元二次方程x2-6x+m=0有实数根,那么m的取值范围是( )
A.m>9 B.m9 C. m<9 D. m≤9
5.把抛物线y=x2+1向右平移3个单位,再向下平移2个单位,得到的抛物线解析式为( )
A.y=(x+3)2-1 B.y=(x+3)2+3
C.y=(x-3)2-1 D.y=(x-3)2+3
6.已知关于x的一元二次方程x2-(k+2)x+k=0,下列说法正确的是( )
A.有两个相等的实数根 B.有两个负数根
C.可以有一根为0 D.没有实数根
7.对于二次函数y=-4(x+6)2-5的图象,下列说法正确的是( )
A.图象与y轴交点的坐标是(0,5) B.对称轴是直线x=6
C.顶点坐标为(-6,5) D.当x<-6时,y随x的增大而增大
8.南宋数学家杨辉的《田亩比类乘除捷法》中有这样的一个问题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何?”其大意是:矩形面积是864平方步,其中长与宽和为60步,问长比宽多多少步?若设长比宽多x步,则下列符合题意的方程是( )
A.(60-x)x=864 B.· =864
C.(60+x)x=864 D.(30+x)(30-x)=864
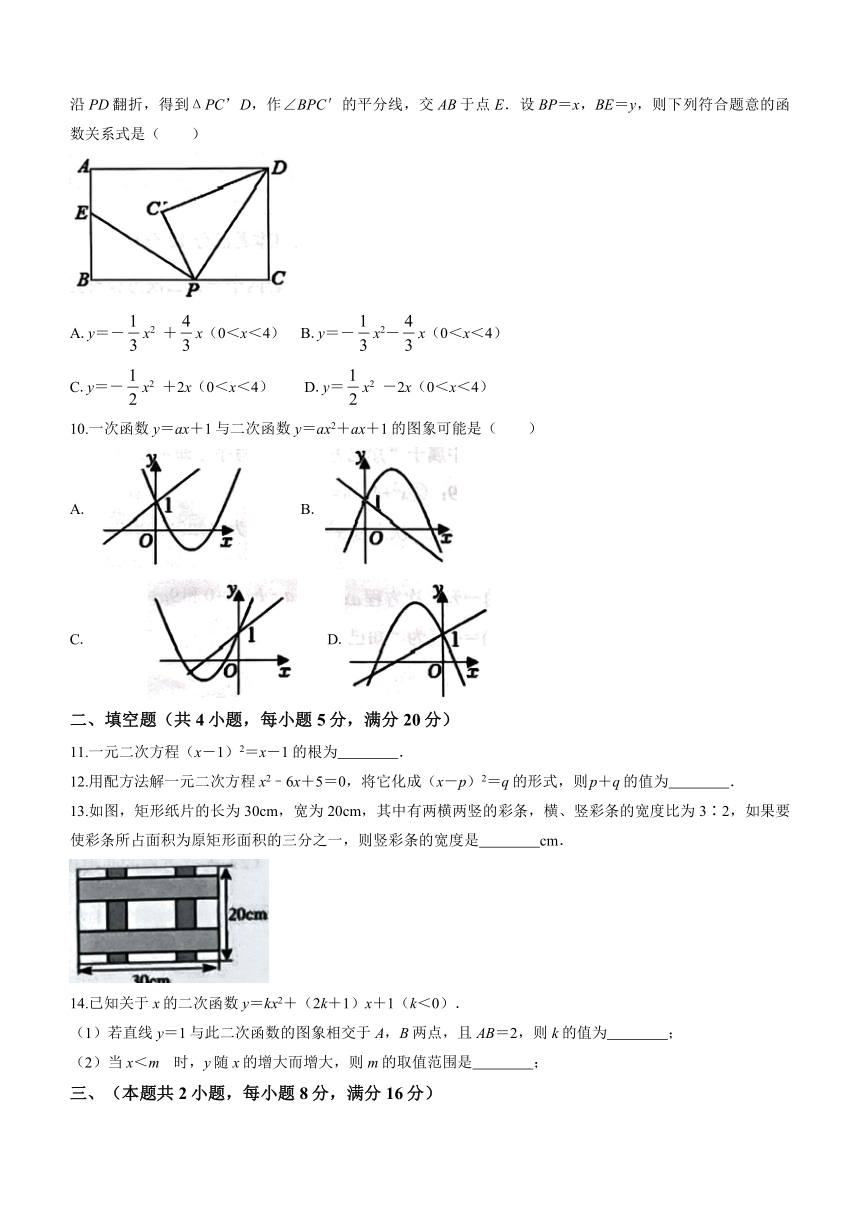
9.如图,矩形ABCD中,BC=4,AB=3,点P是BC边上的动点(点P不与点B、C重合). 现将ΔPCD沿PD翻折,得到ΔPC’D,作∠BPC'的平分线,交AB于点E.设BP=x,BE=y,则下列符合题意的函数关系式是( )
A.y=-x2 +x(0<x<4) B.y=-x2-x(0<x<4)
C.y=-x2 +2x(0<x<4) D.y=x2 -2x(0<x<4)
10.一次函数y=ax+1与二次函数y=ax2+ax+1的图象可能是( )
A. B.
C. D.
二、填空题(共4小题,每小题5分,满分20分)
11.一元二次方程(x-1)2=x-1的根为 .
12.用配方法解一元二次方程x2–6x+5=0,将它化成(x-p)2=q的形式,则 p+q的值为 .
13.如图,矩形纸片的长为30cm,宽为20cm,其中有两横两竖的彩条,横、竖彩条的宽度比为3∶2,如果要使彩条所占面积为原矩形面积的三分之一,则竖彩条的宽度是 cm.
14.已知关于x的二次函数y=kx2+(2k+1)x+1(k<0).
(1)若直线y=1与此二次函数的图象相交于A,B两点,且AB=2,则k的值为 ;
(2)当x<m 时,y随x的增大而增大,则m的取值范围是 ;
三、(本题共2小题,每小题8分,满分16分)
15.解方程:x2-10x+22=0
16.已知二次函数y=x2+6x+k-1(k是常数),如果该二次函数的图象顶点在x轴上,求k的值.
四、(本题共2小题,每题8分,满分16分)
17.二次函数y=ax2与直线y=2x-3交于点(1,b)
(1)求a、b的值;
(2)求抛物线y=ax2与直线y=2x-3的两交点与抛物线的顶点构成的三角形的面积S.
18.已知关于x的一元二次方程kx2+(k-2)x-2=0(k≠0)
(1)求证:这个一元二次方程一定有两个实数根;
(2)若此方程的两根均为整数,求正整数k的值.
五、(本题共2小题,每题10分,满分20分)
19.已知一条抛物线上部分点的横坐标x与纵坐标y的对应值如下表:
x … -1 0 1 2 3 …
y … 0 -3 k -3 0 …
(1)求这条抛物线对应的函数表达式;
(2)求k的值;
(3)这个抛物线经过两点(-2,n)和(m,n),求m的值.
20.为解方程 (x2-2)2-11(x2-2)+18=0,我们可以将x2-2视为一个整体,设x2-2=y则(x2-2)2=y2,于是原方程可转化为y2-11y+18=0,,解此方程,得y1=2,y2=9,当y1=2时,x2-2=2x2=4,∴x=±2;
当y2=9时,x2-2=9x=11,∴x=±.
∴原方程的解为x1=2,x2=-2,x3=-,x4=.
以上方法就是换元法解方程,从而达到了降次的目的,体现了转化的思想.
(1)运用上述换元法解方程:x4-3x2-4=0;
(2)已知实数m,n满足(m+3n)(m+3n-2)=2m+6n-4,求4m+12n-3的值.
六、(本题满分12分)
21.某景区5月份的游客人数比4月份增加60%,6月份的游客人数比5月份减少了10%.
(1)设该景区4月份的游客人数为a万人,请用含a的代数式填表:
月份 4月 5月 6月
游客人数/万人 a
(2)求该景区5、6月这两个月份游客人数的月平均增长率;
(3)景区特色商品营销店推出一款成本价为40元的文化衫,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件售价每降低1元,日销售量增加2件.若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
七、(本题满分12分)
22.若两个一元二次方程有且只有一个相同的实数根,我们就称这两个方程为“知己方程”.例如x2=9和(x+2)(x-3)=0有且只有一个相同的实数根 x=3,所以这两个方程为“知己方程”.
(1)下列方程中属于“知己方程”的是: (只填写序号即可);
①(x-1)2=9; ②x2+4x+4=0 ③x2+2x-8=0;
(2)关于x的一元二次方程x2-2x=0与x2+x+m-1-0为“知己方程”,求m的值;
(3)若关于x的一元二次方程 ax2+bx+c=0 (a≠0)同时满足a-b+c=0和9a+3b+c=0,且与(x-n)(x+3)=0互为“知己方程”,求n的值.
八、(本题满分14分)
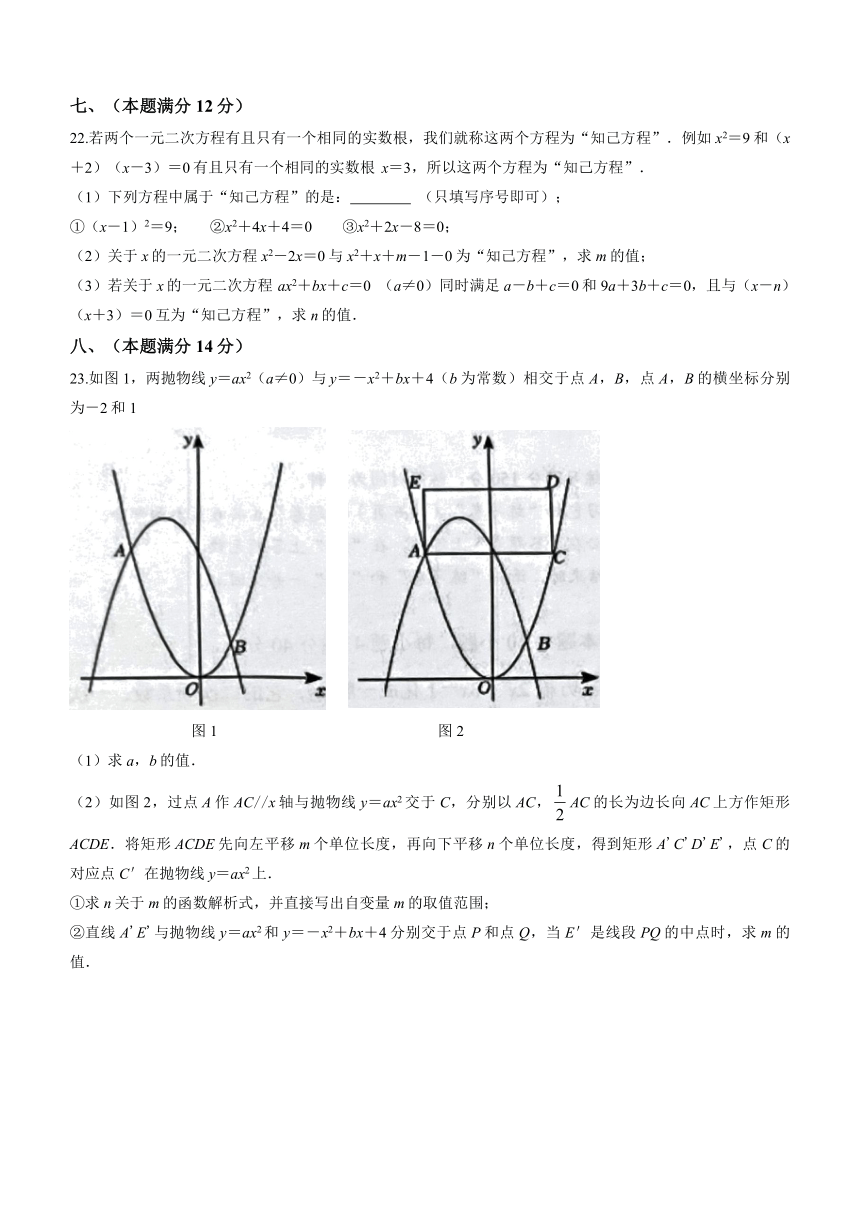
23.如图1,两抛物线y=ax2(a≠0)与 y=-x2+bx+4(b为常数)相交于点A,B,点A,B的横坐标分别为-2和1
图1 图2
(1)求a,b的值.
(2)如图2,过点A作AC//x轴与抛物线y=ax2交于C,分别以AC,AC的长为边长向AC上方作矩形ACDE.将矩形ACDE先向左平移m个单位长度,再向下平移n个单位长度,得到矩形A'C'D'E',点C的对应点C'在抛物线y=ax2上.
①求n关于m的函数解析式,并直接写出自变量m的取值范围;
②直线A'E'与抛物线y=ax2和y=-x2+bx+4分别交于点P和点Q,当E'是线段PQ的中点时,求m的值.
2024届第一学期10月份阶段练习
九年级数学答案
1.A 2.B 3.D 4.D 5.C 6.C 7.D 8.B 9.A 10.C
11. 12.7 13. 14.(1) (2)m≤-1
15.解:移项,得x2-10x=-22,
配方,得x2-10x+25=-22+25,
即(x-5)2=3,
∴x-5=±,
∴x=5±,
即.………………8分
16.解:根据题意,得,
解得k=10……………………8分
17.解:(1)∵直线y=2x-3经过(1,b).
∴b=2-3=-1,
∴函数y=ax2与直线y=2x-3交于(1,-1).
把(1,-1)代入y=ax2(a≠0)得,a=-1;……4分
(2)由解得或,
∴抛物线y=ax2与直线y=2x-3的两交点为(1,-1)和(-3,-9),
把x=0代入y=2x-3得,y=-3,
∴直线y=2x-3与y轴的交点为(0,-3),
∴S=×3×(1+3)=6………………………8分
18.(1)证明:,
∵(k+2)2≥0,
∴△≥0,
∴这个一元二次方程一定有两个实数根;…………4分
(2)解:kx2+(k-2)x-2=0(k≠0),
(kx-2)(x+1)=0,
解得,
∵该方程的两根均为整数,
∴为整数,
∴正整数k的值为1或2………………8分
19.解:(1)设y=a(x+l)(x-3),将(0,-3)代入,
得-3a=-3,解得a=1,
∴抛物线解析式为y=(x+l)(x-3),
即y=x2-2x-3;………………4分
(2)把x=1代入y=x2-2x-3,得y=1-2-3=-4,
∴k=-4;…………6分
(3)∵图象经过点(-1,0),(3,0),
∴抛物线的对称轴为直线,
∵二次函数的图象经过点(-2,n)和(m,n)两点,
∴=1,
∴m=4………………10分
20.解:(1)设x2=y,
则原方程可转化为y2-3y-4=0,
解得y1=4,y2=-1,
当y1=4时,x2=4,∴x=±2;
当y2=-1,x2=-1,此方程无解.
∴原方程的解为;……………………5分
(2)∵(m+3n)((m+3n-2)=2m+6n-4,
∴(m+3n)(m+3n-2)=2(m+3n)-4,
设m+3n=t,则原方程可化为t(t-2)=2t-4,
整理,得t2-4t+4=(t-2)2=0,修改为:t2-4t+4=0即(t-2)2=0
解得t=2,
∴m+3n=2,
∴4m+12n-3=4(m+3n)-3=4×2-3=5…………………10分
21.解:(1)1.6a,1.44a;………………2分
(2)该景区5、6这两个月游客人数的月平均增长率为x,
根据题意,得a(1+x)2=1.44a,
解得(不符合题意,舍去)
答:该景区5、6这两个月游客人数的月平均增长率为20%;……………6分
(3)设每件的售价定为y元,则每件的销售利润为(y-40)元,每天可卖出20+2(60-y)=(140-2y)件,
根据题意,得(y-40)(140-2y)=(60-40)×20,
整理,得y2-110y+3000=0,
解得y1=50,y2=60不符合题意,舍去)
答:每件售价应定为50元.………………12分
22.(1)①②;……………………………………2分
(2)一元二次方程x2-2x=0的解为,
当相同的根是x=0时,则m-1=0,解得m=1;
当相同的根是x=2时,则4+2+m-1=0,解得m=-5;
综上,m的值为1或-5;………………7分
(3)∵关于x的一元二次方程ax2+bx+c=0(a≠0)同时满足a-b+c=0和9a+3b+c=0,
∴关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根是;
∵(x-n)(x+3)=0的两个根是,
∵关于x的一元二次方程ax2+bx+c=0(a≠0)与(x-n)(x+3)=0互为“知己方程”,
∴n=-1或3……………………12分
23.(1)由题意,得
当x=-2时,4a=-4-2b+4,
当x=1时,a=-1+b+4,
解方程组
得a=1,b=-2;………………4分
(2)①由(1)知两抛物线分别为y=x2与y=-x2-2x+4,
AC=4,AE=2,点E(-2,6),点C(2,4),
则平移后点为(2-m,4-n),
将点的坐标代入抛物线y=x2,得4-n=(2-m)2,
即n=-m2+4m,
自变量m的取值范围:0<m<4;………………8分
②由①知,点坐标为(-2-m,4-n)即(-2-m,m2-4m+4),
点的坐标为(-2-m,m2-4m+6),
则点P的坐标为(-2-m,m2+4m+4),
点Q的坐标为(-2-m,-m2-2m+4),
则点PQ中点的坐标为(-2-m,m+4),
当是PQ的中点时,则m2-4m+6=m+4,
解得(由0<m<4知,不合题意,舍去),
………14分
注:解答题只要解法合理,均相应给分
九年级数学
注意事项:
1.数学练习满分150分,练习时间为120分钟.
2.本练习包括“练习卷”(共6页)和“答题卷”(共6页)两部分.
3.请务必在“答题卷”上答题,在“练习卷”上答题无效.
4.练习结束时,请将“练习卷”和“答题卷”一并交回.
一、选择题(本题共10小题,每小题4分,满分40分)
1.将一元二次方程2x2-3x=1化成一般形式后,它的二次项系数、一次项系数和常数项分别为( )
A.2,-3,-1 B.2,-3,1 C.-2,3,-1 D.-2,-3,1
2.下列函数解析式中,y一定是x的二次函数的是( )
A.y=x2-+1 B. y=2x2 C.y=(m-3)x2+x-1 D.y=ax2+bx+c
3.若关于x的一元二次方程x2-ax+6=0的一个根是2,则a的值为( )
A.2 B.3 C.4 D.5
4.如果关于x的一元二次方程x2-6x+m=0有实数根,那么m的取值范围是( )
A.m>9 B.m9 C. m<9 D. m≤9
5.把抛物线y=x2+1向右平移3个单位,再向下平移2个单位,得到的抛物线解析式为( )
A.y=(x+3)2-1 B.y=(x+3)2+3
C.y=(x-3)2-1 D.y=(x-3)2+3
6.已知关于x的一元二次方程x2-(k+2)x+k=0,下列说法正确的是( )
A.有两个相等的实数根 B.有两个负数根
C.可以有一根为0 D.没有实数根
7.对于二次函数y=-4(x+6)2-5的图象,下列说法正确的是( )
A.图象与y轴交点的坐标是(0,5) B.对称轴是直线x=6
C.顶点坐标为(-6,5) D.当x<-6时,y随x的增大而增大
8.南宋数学家杨辉的《田亩比类乘除捷法》中有这样的一个问题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何?”其大意是:矩形面积是864平方步,其中长与宽和为60步,问长比宽多多少步?若设长比宽多x步,则下列符合题意的方程是( )
A.(60-x)x=864 B.· =864
C.(60+x)x=864 D.(30+x)(30-x)=864
9.如图,矩形ABCD中,BC=4,AB=3,点P是BC边上的动点(点P不与点B、C重合). 现将ΔPCD沿PD翻折,得到ΔPC’D,作∠BPC'的平分线,交AB于点E.设BP=x,BE=y,则下列符合题意的函数关系式是( )
A.y=-x2 +x(0<x<4) B.y=-x2-x(0<x<4)
C.y=-x2 +2x(0<x<4) D.y=x2 -2x(0<x<4)
10.一次函数y=ax+1与二次函数y=ax2+ax+1的图象可能是( )
A. B.
C. D.
二、填空题(共4小题,每小题5分,满分20分)
11.一元二次方程(x-1)2=x-1的根为 .
12.用配方法解一元二次方程x2–6x+5=0,将它化成(x-p)2=q的形式,则 p+q的值为 .
13.如图,矩形纸片的长为30cm,宽为20cm,其中有两横两竖的彩条,横、竖彩条的宽度比为3∶2,如果要使彩条所占面积为原矩形面积的三分之一,则竖彩条的宽度是 cm.
14.已知关于x的二次函数y=kx2+(2k+1)x+1(k<0).
(1)若直线y=1与此二次函数的图象相交于A,B两点,且AB=2,则k的值为 ;
(2)当x<m 时,y随x的增大而增大,则m的取值范围是 ;
三、(本题共2小题,每小题8分,满分16分)
15.解方程:x2-10x+22=0
16.已知二次函数y=x2+6x+k-1(k是常数),如果该二次函数的图象顶点在x轴上,求k的值.
四、(本题共2小题,每题8分,满分16分)
17.二次函数y=ax2与直线y=2x-3交于点(1,b)
(1)求a、b的值;
(2)求抛物线y=ax2与直线y=2x-3的两交点与抛物线的顶点构成的三角形的面积S.
18.已知关于x的一元二次方程kx2+(k-2)x-2=0(k≠0)
(1)求证:这个一元二次方程一定有两个实数根;
(2)若此方程的两根均为整数,求正整数k的值.
五、(本题共2小题,每题10分,满分20分)
19.已知一条抛物线上部分点的横坐标x与纵坐标y的对应值如下表:
x … -1 0 1 2 3 …
y … 0 -3 k -3 0 …
(1)求这条抛物线对应的函数表达式;
(2)求k的值;
(3)这个抛物线经过两点(-2,n)和(m,n),求m的值.
20.为解方程 (x2-2)2-11(x2-2)+18=0,我们可以将x2-2视为一个整体,设x2-2=y则(x2-2)2=y2,于是原方程可转化为y2-11y+18=0,,解此方程,得y1=2,y2=9,当y1=2时,x2-2=2x2=4,∴x=±2;
当y2=9时,x2-2=9x=11,∴x=±.
∴原方程的解为x1=2,x2=-2,x3=-,x4=.
以上方法就是换元法解方程,从而达到了降次的目的,体现了转化的思想.
(1)运用上述换元法解方程:x4-3x2-4=0;
(2)已知实数m,n满足(m+3n)(m+3n-2)=2m+6n-4,求4m+12n-3的值.
六、(本题满分12分)
21.某景区5月份的游客人数比4月份增加60%,6月份的游客人数比5月份减少了10%.
(1)设该景区4月份的游客人数为a万人,请用含a的代数式填表:
月份 4月 5月 6月
游客人数/万人 a
(2)求该景区5、6月这两个月份游客人数的月平均增长率;
(3)景区特色商品营销店推出一款成本价为40元的文化衫,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件售价每降低1元,日销售量增加2件.若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
七、(本题满分12分)
22.若两个一元二次方程有且只有一个相同的实数根,我们就称这两个方程为“知己方程”.例如x2=9和(x+2)(x-3)=0有且只有一个相同的实数根 x=3,所以这两个方程为“知己方程”.
(1)下列方程中属于“知己方程”的是: (只填写序号即可);
①(x-1)2=9; ②x2+4x+4=0 ③x2+2x-8=0;
(2)关于x的一元二次方程x2-2x=0与x2+x+m-1-0为“知己方程”,求m的值;
(3)若关于x的一元二次方程 ax2+bx+c=0 (a≠0)同时满足a-b+c=0和9a+3b+c=0,且与(x-n)(x+3)=0互为“知己方程”,求n的值.
八、(本题满分14分)
23.如图1,两抛物线y=ax2(a≠0)与 y=-x2+bx+4(b为常数)相交于点A,B,点A,B的横坐标分别为-2和1
图1 图2
(1)求a,b的值.
(2)如图2,过点A作AC//x轴与抛物线y=ax2交于C,分别以AC,AC的长为边长向AC上方作矩形ACDE.将矩形ACDE先向左平移m个单位长度,再向下平移n个单位长度,得到矩形A'C'D'E',点C的对应点C'在抛物线y=ax2上.
①求n关于m的函数解析式,并直接写出自变量m的取值范围;
②直线A'E'与抛物线y=ax2和y=-x2+bx+4分别交于点P和点Q,当E'是线段PQ的中点时,求m的值.
2024届第一学期10月份阶段练习
九年级数学答案
1.A 2.B 3.D 4.D 5.C 6.C 7.D 8.B 9.A 10.C
11. 12.7 13. 14.(1) (2)m≤-1
15.解:移项,得x2-10x=-22,
配方,得x2-10x+25=-22+25,
即(x-5)2=3,
∴x-5=±,
∴x=5±,
即.………………8分
16.解:根据题意,得,
解得k=10……………………8分
17.解:(1)∵直线y=2x-3经过(1,b).
∴b=2-3=-1,
∴函数y=ax2与直线y=2x-3交于(1,-1).
把(1,-1)代入y=ax2(a≠0)得,a=-1;……4分
(2)由解得或,
∴抛物线y=ax2与直线y=2x-3的两交点为(1,-1)和(-3,-9),
把x=0代入y=2x-3得,y=-3,
∴直线y=2x-3与y轴的交点为(0,-3),
∴S=×3×(1+3)=6………………………8分
18.(1)证明:,
∵(k+2)2≥0,
∴△≥0,
∴这个一元二次方程一定有两个实数根;…………4分
(2)解:kx2+(k-2)x-2=0(k≠0),
(kx-2)(x+1)=0,
解得,
∵该方程的两根均为整数,
∴为整数,
∴正整数k的值为1或2………………8分
19.解:(1)设y=a(x+l)(x-3),将(0,-3)代入,
得-3a=-3,解得a=1,
∴抛物线解析式为y=(x+l)(x-3),
即y=x2-2x-3;………………4分
(2)把x=1代入y=x2-2x-3,得y=1-2-3=-4,
∴k=-4;…………6分
(3)∵图象经过点(-1,0),(3,0),
∴抛物线的对称轴为直线,
∵二次函数的图象经过点(-2,n)和(m,n)两点,
∴=1,
∴m=4………………10分
20.解:(1)设x2=y,
则原方程可转化为y2-3y-4=0,
解得y1=4,y2=-1,
当y1=4时,x2=4,∴x=±2;
当y2=-1,x2=-1,此方程无解.
∴原方程的解为;……………………5分
(2)∵(m+3n)((m+3n-2)=2m+6n-4,
∴(m+3n)(m+3n-2)=2(m+3n)-4,
设m+3n=t,则原方程可化为t(t-2)=2t-4,
整理,得t2-4t+4=(t-2)2=0,修改为:t2-4t+4=0即(t-2)2=0
解得t=2,
∴m+3n=2,
∴4m+12n-3=4(m+3n)-3=4×2-3=5…………………10分
21.解:(1)1.6a,1.44a;………………2分
(2)该景区5、6这两个月游客人数的月平均增长率为x,
根据题意,得a(1+x)2=1.44a,
解得(不符合题意,舍去)
答:该景区5、6这两个月游客人数的月平均增长率为20%;……………6分
(3)设每件的售价定为y元,则每件的销售利润为(y-40)元,每天可卖出20+2(60-y)=(140-2y)件,
根据题意,得(y-40)(140-2y)=(60-40)×20,
整理,得y2-110y+3000=0,
解得y1=50,y2=60不符合题意,舍去)
答:每件售价应定为50元.………………12分
22.(1)①②;……………………………………2分
(2)一元二次方程x2-2x=0的解为,
当相同的根是x=0时,则m-1=0,解得m=1;
当相同的根是x=2时,则4+2+m-1=0,解得m=-5;
综上,m的值为1或-5;………………7分
(3)∵关于x的一元二次方程ax2+bx+c=0(a≠0)同时满足a-b+c=0和9a+3b+c=0,
∴关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根是;
∵(x-n)(x+3)=0的两个根是,
∵关于x的一元二次方程ax2+bx+c=0(a≠0)与(x-n)(x+3)=0互为“知己方程”,
∴n=-1或3……………………12分
23.(1)由题意,得
当x=-2时,4a=-4-2b+4,
当x=1时,a=-1+b+4,
解方程组
得a=1,b=-2;………………4分
(2)①由(1)知两抛物线分别为y=x2与y=-x2-2x+4,
AC=4,AE=2,点E(-2,6),点C(2,4),
则平移后点为(2-m,4-n),
将点的坐标代入抛物线y=x2,得4-n=(2-m)2,
即n=-m2+4m,
自变量m的取值范围:0<m<4;………………8分
②由①知,点坐标为(-2-m,4-n)即(-2-m,m2-4m+4),
点的坐标为(-2-m,m2-4m+6),
则点P的坐标为(-2-m,m2+4m+4),
点Q的坐标为(-2-m,-m2-2m+4),
则点PQ中点的坐标为(-2-m,m+4),
当是PQ的中点时,则m2-4m+6=m+4,
解得(由0<m<4知,不合题意,舍去),
………14分
注:解答题只要解法合理,均相应给分
同课章节目录
