12.2三角形全等的判定——倍长中线模型 讲义(无答案) 2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 12.2三角形全等的判定——倍长中线模型 讲义(无答案) 2023—2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 125.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 00:00:00 | ||
图片预览

文档简介
全等三角形的判定——倍长中线模型
模型分析:遇到中线的问题,可以通过倍长中线,证明三角形全等,会让题目中分散的条件集中起来,达到解题的目的。
类型一:已知,在三角形 ABC中,O为BC边中点。
(辅助线作法一)延长AO到点D使AO=DO, 连接CD,
求证:△AOB≌△DOC,AB=CD,AB//CD
(辅助线作法二),过点C作CD//AB,与AO的延长线交于点D,则△AOB≌△DOC,理由是:____________
练习1:如图,在△ABC中,AD是BC边上的中线,AC=3,AD=5,求AB的取值范围
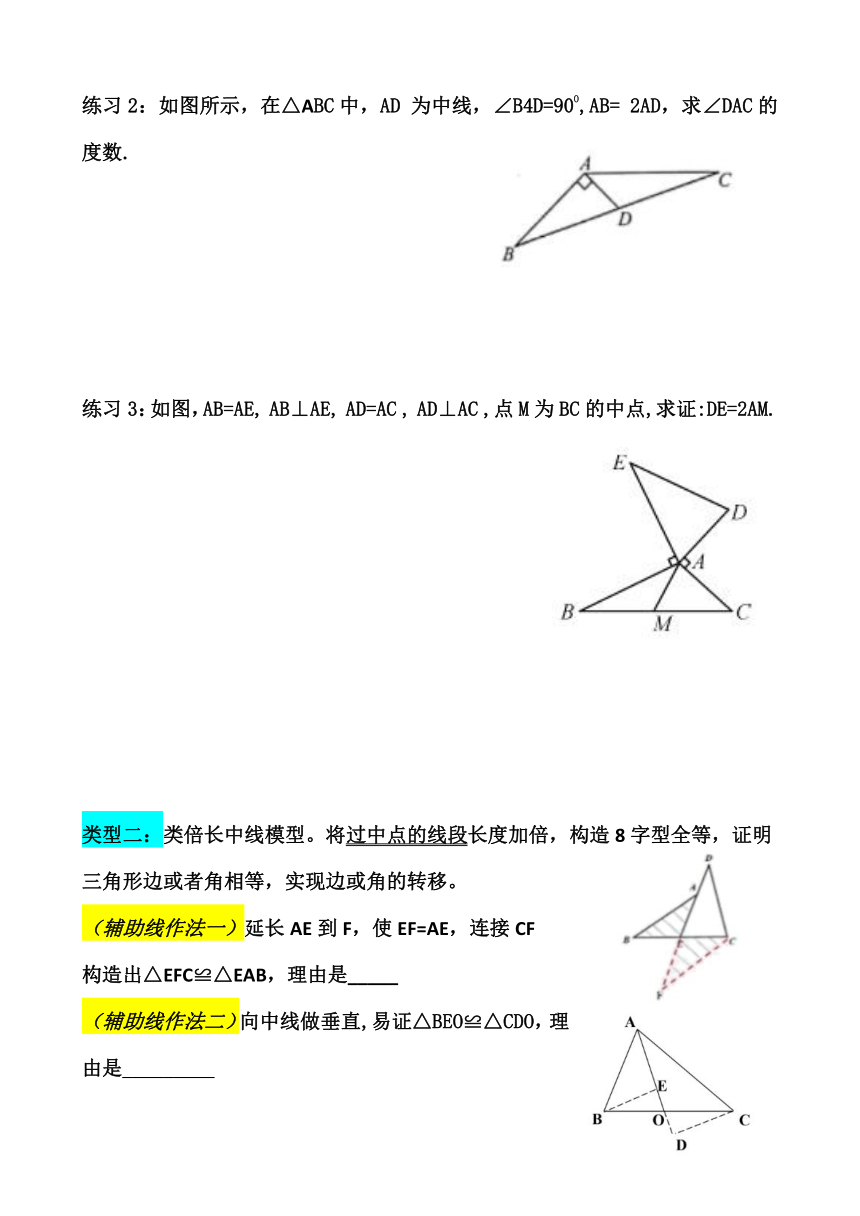
练习2:如图所示,在△ABC中,AD 为中线,∠B4D=90O,AB= 2AD,求∠DAC的度数.
练习3:如图,AB=AE, AB⊥AE, AD=AC , AD⊥AC ,点M为BC的中点,求证:DE=2AM.
类型二:类倍长中线模型。将过中点的线段长度加倍,构造8字型全等,证明三角形边或者角相等,实现边或角的转移。
(辅助线作法一)延长AE到F,使EF=AE,连接CF
构造出△EFC≌△EAB,理由是_____
(辅助线作法二)向中线做垂直,易证△BEO≌△CDO,理由是_________
练习4: 已知,如图E是BC的中点,点A在DE上,且∠BAE=∠CDE。求证: AB=CD.
(辅助线作法一)
(辅助线作法二)
练习5:如图,AD是△ABC的中线,E,F分别在边AB,AC上(E,F不与端点重合)且DE⊥DF,则( )
A. BE+CF > EF B. BE+CF= EF
D. BE+CF< EF D. BE+CF与EF的长短关系不确定
作业:数学课上,老师给出了如下问题:
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF。求证: AC=BF.
经过讨论,同学们得到以下两种思路:
思路一如图①,添加辅助线后依据SAS可证得△ADC≌OGDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
思路二如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
完成下面问题:
(1)思路一的辅助线的作法是:________________________
思路二的辅助线的作法是:__________________________
(2)请你选其中一种思路,写出具体证明过程。
模型分析:遇到中线的问题,可以通过倍长中线,证明三角形全等,会让题目中分散的条件集中起来,达到解题的目的。
类型一:已知,在三角形 ABC中,O为BC边中点。
(辅助线作法一)延长AO到点D使AO=DO, 连接CD,
求证:△AOB≌△DOC,AB=CD,AB//CD
(辅助线作法二),过点C作CD//AB,与AO的延长线交于点D,则△AOB≌△DOC,理由是:____________
练习1:如图,在△ABC中,AD是BC边上的中线,AC=3,AD=5,求AB的取值范围
练习2:如图所示,在△ABC中,AD 为中线,∠B4D=90O,AB= 2AD,求∠DAC的度数.
练习3:如图,AB=AE, AB⊥AE, AD=AC , AD⊥AC ,点M为BC的中点,求证:DE=2AM.
类型二:类倍长中线模型。将过中点的线段长度加倍,构造8字型全等,证明三角形边或者角相等,实现边或角的转移。
(辅助线作法一)延长AE到F,使EF=AE,连接CF
构造出△EFC≌△EAB,理由是_____
(辅助线作法二)向中线做垂直,易证△BEO≌△CDO,理由是_________
练习4: 已知,如图E是BC的中点,点A在DE上,且∠BAE=∠CDE。求证: AB=CD.
(辅助线作法一)
(辅助线作法二)
练习5:如图,AD是△ABC的中线,E,F分别在边AB,AC上(E,F不与端点重合)且DE⊥DF,则( )
A. BE+CF > EF B. BE+CF= EF
D. BE+CF< EF D. BE+CF与EF的长短关系不确定
作业:数学课上,老师给出了如下问题:
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF。求证: AC=BF.
经过讨论,同学们得到以下两种思路:
思路一如图①,添加辅助线后依据SAS可证得△ADC≌OGDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
思路二如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
完成下面问题:
(1)思路一的辅助线的作法是:________________________
思路二的辅助线的作法是:__________________________
(2)请你选其中一种思路,写出具体证明过程。
