12.2 三角形全等的判定 周末习题 (无答案)2023—2024学年人教版八年级数学上册
文档属性
| 名称 | 12.2 三角形全等的判定 周末习题 (无答案)2023—2024学年人教版八年级数学上册 | 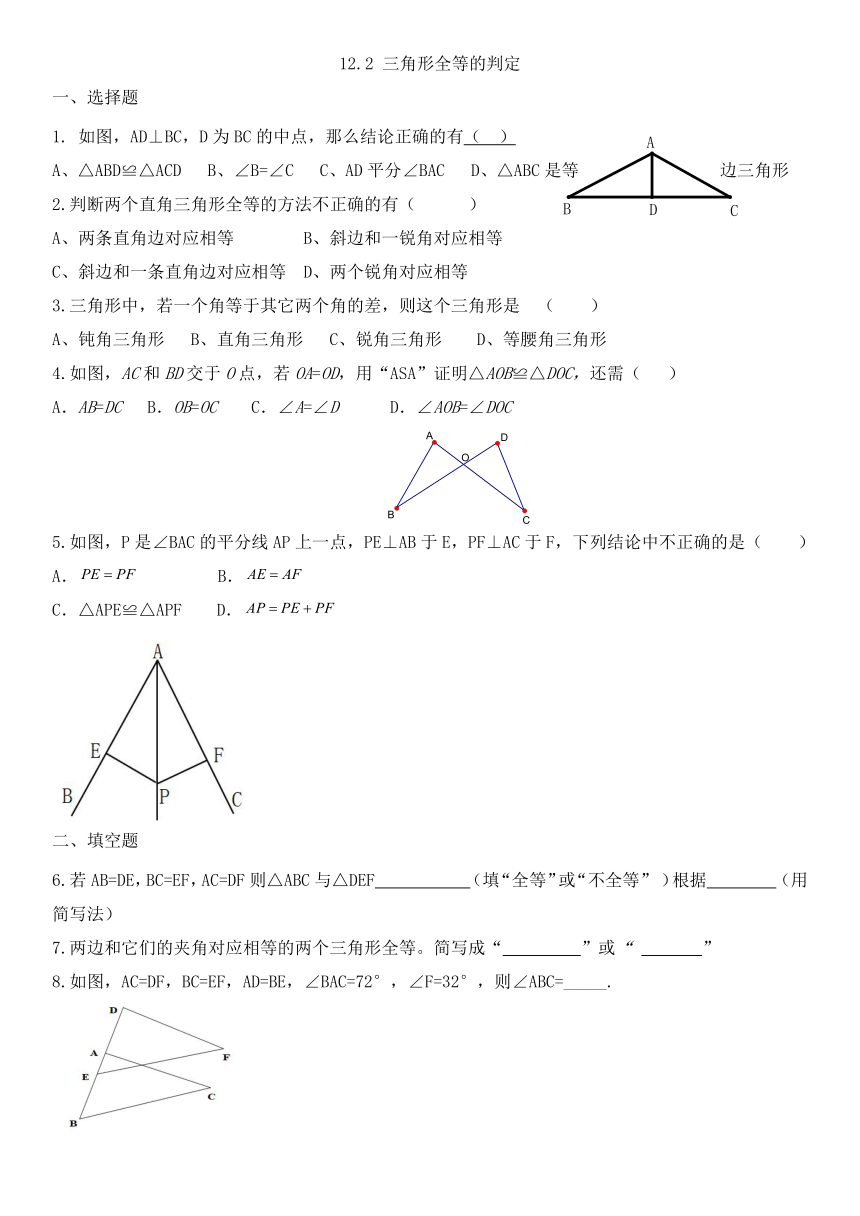 | |
| 格式 | docx | ||
| 文件大小 | 75.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 19:14:51 | ||
图片预览

文档简介
12.2 三角形全等的判定
选择题
1. 如图,AD⊥BC,D为BC的中点,那么结论正确的有( )
A、△ABD≌△ACD B、∠B=∠C C、AD平分∠BAC D、△ABC是等边三角形
2.判断两个直角三角形全等的方法不正确的有( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两个锐角对应相等
3.三角形中,若一个角等于其它两个角的差,则这个三角形是 ( )
A、钝角三角形 B、直角三角形 C、锐角三角形 D、等腰角三角形
4.如图,AC和BD交于O点,若OA=OD,用“ASA”证明△AOB≌△DOC,还需( )
A.AB=DC B.OB=OC C.∠A=∠D D.∠AOB=∠DOC
5.如图,P是∠BAC的平分线AP上一点,PE⊥AB于E,PF⊥AC于F,下列结论中不正确的是( )
A. B.
C.△APE≌△APF D.
填空题
6.若AB=DE,BC=EF,AC=DF则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
7.两边和它们的夹角对应相等的两个三角形全等。简写成“ ”或“ ”
8.如图,AC=DF,BC=EF,AD=BE,∠BAC=72°,∠F=32°,则∠ABC=_____.
9.A、D、C、F在同一直线上,ED⊥AF,BC⊥AF,AB=EF=10,BC=ED=6,依据 得△ABC≌△FED,则△FED的周长是 。
10.如图,已知AD∥BC,AD=CB,要用边角边公理证明△ABC≌△CDA,需要三个条件,这三个条件中,已具有两个条件,一是AD=CB(已知),二是___________;还需要一个条件________ 。
11.如图,AC、BD相交于点O,∠A=∠D,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是 .
解答题
12.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
13.如图 ,AB=AD,CB=CD,求证:△ABC≌△ADC
14.如图,四边形ABCD是正方形,点G是BC上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.求证:AF=BF+EF
15.如图,已知D是∠BAC内部一点,DF⊥AB, DE⊥AC,F,E分别是垂足,且DF=DE,则点D在∠BAC的角平分线上。请说明理由。
16.如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
选择题
1. 如图,AD⊥BC,D为BC的中点,那么结论正确的有( )
A、△ABD≌△ACD B、∠B=∠C C、AD平分∠BAC D、△ABC是等边三角形
2.判断两个直角三角形全等的方法不正确的有( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两个锐角对应相等
3.三角形中,若一个角等于其它两个角的差,则这个三角形是 ( )
A、钝角三角形 B、直角三角形 C、锐角三角形 D、等腰角三角形
4.如图,AC和BD交于O点,若OA=OD,用“ASA”证明△AOB≌△DOC,还需( )
A.AB=DC B.OB=OC C.∠A=∠D D.∠AOB=∠DOC
5.如图,P是∠BAC的平分线AP上一点,PE⊥AB于E,PF⊥AC于F,下列结论中不正确的是( )
A. B.
C.△APE≌△APF D.
填空题
6.若AB=DE,BC=EF,AC=DF则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
7.两边和它们的夹角对应相等的两个三角形全等。简写成“ ”或“ ”
8.如图,AC=DF,BC=EF,AD=BE,∠BAC=72°,∠F=32°,则∠ABC=_____.
9.A、D、C、F在同一直线上,ED⊥AF,BC⊥AF,AB=EF=10,BC=ED=6,依据 得△ABC≌△FED,则△FED的周长是 。
10.如图,已知AD∥BC,AD=CB,要用边角边公理证明△ABC≌△CDA,需要三个条件,这三个条件中,已具有两个条件,一是AD=CB(已知),二是___________;还需要一个条件________ 。
11.如图,AC、BD相交于点O,∠A=∠D,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是 .
解答题
12.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
13.如图 ,AB=AD,CB=CD,求证:△ABC≌△ADC
14.如图,四边形ABCD是正方形,点G是BC上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.求证:AF=BF+EF
15.如图,已知D是∠BAC内部一点,DF⊥AB, DE⊥AC,F,E分别是垂足,且DF=DE,则点D在∠BAC的角平分线上。请说明理由。
16.如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
