第八单元数学广角-数与形易错题大集结-数学六年级上册人教版(含解析)
文档属性
| 名称 | 第八单元数学广角-数与形易错题大集结-数学六年级上册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 19:34:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第八单元数学广角-数与形易错题大集结-数学六年级上册人教版
一、选择题
1.按规律摆六边形,如果摆n个六边形,需要( )根小棒。
A.6n B. C.
2.如图所示,用黑白两种颜色的正五边形地砖按下图所示的规律,拼成若干个蝴蝶图案,则第7个蝴蝶图案中白色地砖有( )。
A.35块 B.27块 C.22块 D.7块
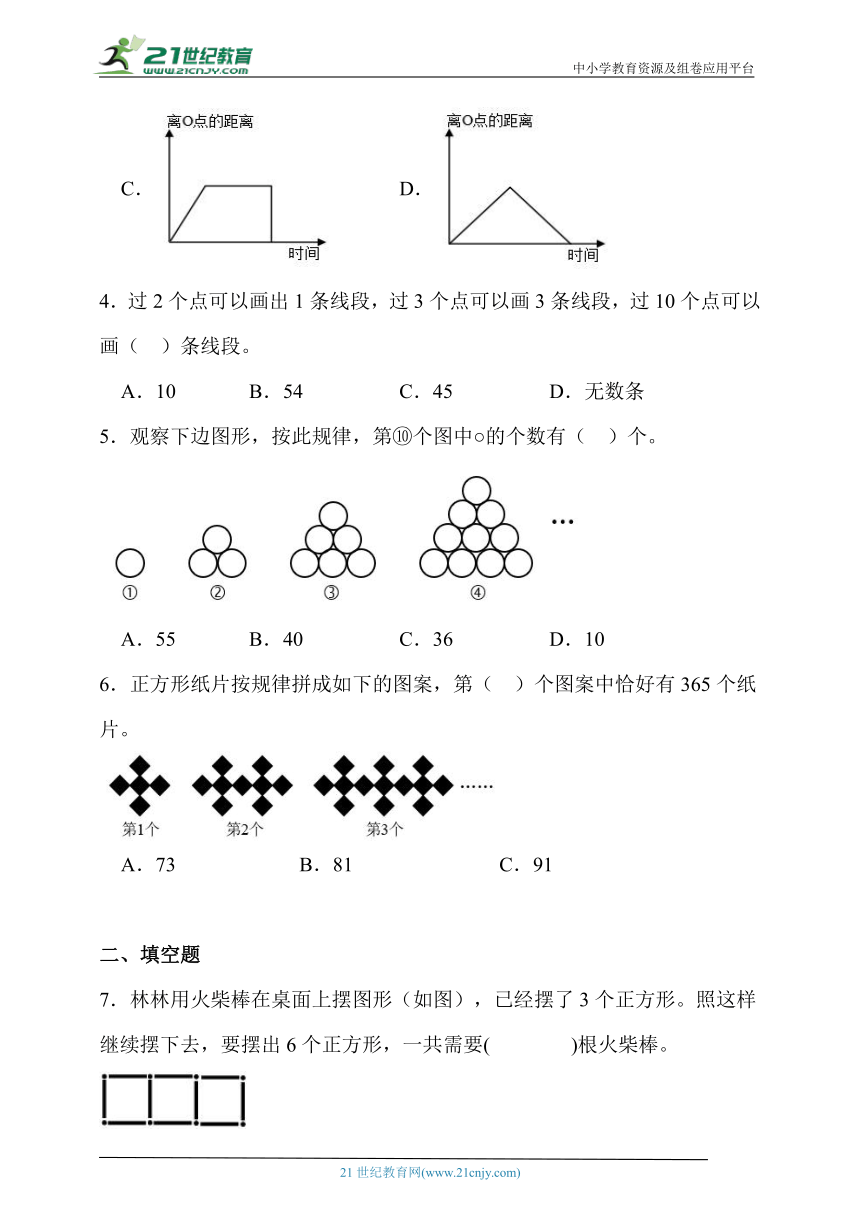
3.小蚂蚁从O点出发,围绕一块扇形奶酪爬一周(如图)。下面( )幅图描述了它的活动行程。
A. B.
C. D.
4.过2个点可以画出1条线段,过3个点可以画3条线段,过10个点可以画( )条线段。
A.10 B.54 C.45 D.无数条
5.观察下边图形,按此规律,第⑩个图中○的个数有( )个。
A.55 B.40 C.36 D.10
6.正方形纸片按规律拼成如下的图案,第( )个图案中恰好有365个纸片。
A.73 B.81 C.91
二、填空题
7.林林用火柴棒在桌面上摆图形(如图),已经摆了3个正方形。照这样继续摆下去,要摆出6个正方形,一共需要( )根火柴棒。
8.根据图形中各个数的关系,★=( ),▲=( )。
9.如下图,先把三角形各边的中点连接起来,组成第2个三角形。再把这个三角形的中点连接起来,组成第3个三角形……已知最大三角形的面积是2平方分米,第( )个三角形的面积是平方分米。
10.按规律填空:2、5、10、17、26、37…第n个数是( )。
11.古希腊著名的毕达哥拉斯学派经常把“形”与“数”联系在一起,下图是用“形”来表示“数”、请你认真观察:第1幅图的点数为1,第2幅图的点数为5,第3幅图的点数为9,依次排下去,第10幅图的点数为( ),第n幅图的点数为( )。
12.4个边长为1cm小正方形组成图形。下面这一列图形由重叠而成。按这样的方式重叠,第(5)个图形的周长是( )cm。
13.牛牛摆“星星”如图所示,摆第1个图形需3颗★,摆第2个图形需6颗★,……,摆第5个图形需( )颗★。像这样,摆第n个图形需要( )颗★。
14.用黑、白两种颜色的圆摆图形。
……
像这样继续摆下去,摆第5幅图需要( )个〇;摆第n幅图需要( )个〇。
三、解答题
15.小兔想做一个正方形的画框,可是它的细木条长短都不一样,有1,2,3,4,5,6,7,8,9厘米长的细木条各一根.
(1)如果不能锯断,但可以连接(接头处不计损耗),小兔可以做一个怎样的正方形画框?
(2)要做边长是9厘米的正方形的画框,可以怎么做?
16.一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人,照这样,10张桌子并成一排可以坐多少人?如果一共有38人,需要并多少张桌子才能坐下?
17.按照右边的方法堆木头,如果底层放9根木头,完成堆放后,木头的总根数是多少根?
18.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.请写出第5个图形的算式.
4=1+3 9=3+6 16=6+10
19.将一些小圆点按一定的规律摆放,所得到的图形依次为第1个图形、第2个图形、第3个图形、第4个图形.如下图所示,各个图形的小圆点个数依次是6个、10个、16个、24个……
第1个图形 第2个图形 第3个图形 第4个图形
(1)第8个图形一共有多少个小圆点
(2)已知连续两个图形的小圆点的个数差是100个.这两个图形分别是第个______图形和第个______图形.
20.用花、白两种正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用花瓷砖(如图所示)。
(1)填写下列表格。
大正方形每边的瓷砖块数 3 4 5 6 7 …
花瓷砖块数 8 …
(2)如果所拼的图形中,用了20块花瓷砖,那么白瓷砖用了多少块?
(3)如果所拼的图形中,用了n2块白瓷砖,那么花瓷砖用了多少块?
参考答案:
1.B
【分析】观察可知,小棒数量=六边形数量×5+1,据此分析。
【详解】n×5+1=5n+1=1+5n
故答案为:B
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
2.C
【分析】观察图形,第1个图形白色砖的数量是:4=3+1;
第2个图形白色砖的数量是:7=3×2+1;
第3个图形白色砖的数量是:10=3×3+1;
可以得出规律:第n个蝴蝶图案中白色地砖有块;据此解答。
【详解】由分析可知,第n个蝴蝶图案中白色地砖有块,
当时,白色地砖数量为3×7+1=22(块)。
【点睛】此题考查了数与形的规律问题,关键是结合图形数量之间的运算关系,找出规律即可。
3.B
【分析】一只蚂蚁从O点出发,沿着扇形的边缘匀速爬行,在开始时经过第一段时,蚂蚁到O点的距离随运动时间t的增大而增大;到第二段弧形这段路程时,蚂蚁到O点的距离S不变,到第三段时,走的是另一条半径,蚂蚁到O点的距离随运动时间t的增大而减小。据此解答。
【详解】A.第三段路程随着时间的增大还在增大,不符合题意;
B.第一段随着时间的增大,路程也在增大,第二段路程不变,第三段随着时间的增加,路程在减小。符合题意;
C.第三段路程在减少,时间却不变,显然不符合题意;
D.只有第一段和第三段路程的表述,第二段路程不变并没有在图形中体现出来,不符合题意;
故答案为:B
【点睛】根据蚂蚁在扇形上运动时,随着时间的变化,距离不断发生变化,从而得出图像的特点,即可得出结论。
4.C
【分析】如图:
2个点,1条线段;
3个点,3条线段,3=3×2÷2;
4个点,6条线段,6=4×3÷2;
5个点,10条线段,10=5×4÷2;
……
规律:点的个数为n(n≥2),可以画的线段为:条;
据此规律,得出过10个点可以画的线段的条数。
【详解】规律:点的个数为n(n≥2),可以画的线段为:条;
n=10时
=
(条)
过10个点可以画45条线段。
故答案为:C
【点睛】本题是找规律的题型,通过画图发现点数与线段的规律,利用规律解答。
5.A
【分析】第几个图中就有几层,且每层圆的个数与层数相同,据此把各层圆的个数进行求和解答。
【详解】图①中圆的个数:1=1
图②中圆的个数:3=1+2
图③中圆的个数:6=1+2+3
图④中圆的个数:10=1+2+3+4
……
图⑩中圆的个数:55=1+2+3+4+……+10
故答案为:A
【点睛】本题考查运用数形结合的方法探究数学规律,注意要把图形和数一一对应。
6.C
【分析】由题干可知,第1个图案中有纸片的个数:5=1+4×1;
第2个图案中有纸片的个数:9=1+4×2;
第3个图案中有纸片的个数:13=1+4×3;
……
第n个图案中有纸片的个数:4n+1,据此解答。
【详解】(365-1)÷4
=364÷4
=91(个)
所以第91个图案中恰好有365个纸片。
故答案为:C
【点睛】此题考查的是找规律,正确找出规律并用规律解决问题是解题关键。
7.19
【分析】摆1个正方形需要4根火柴棒,每增加1个正方形,需要增加3根火柴棒。则摆2个正方形需要(4+3)根火柴棒,摆3个正方形需要(4+2×3)根火柴棒。摆6个正方形需要(4+5×3)根火柴棒。据此解答。
【详解】4+(6-1)×3
=4+5×3
=4+15
=19(根)
一共需要19根火柴棒。
【点睛】解决本题的关键是明确正方形个数与火柴棒根数之间的关系,再根据这个关系解决问题。
8. 26 32
【分析】由图分析可知,黑色三角形位置的数字是16的2倍,五角星星位置的数字是比16多10。
【详解】★=16+10=26
▲=16×2=32
【点睛】此题考查学生的观察推理能力。
9.5
【分析】根据题意,先把三角形各边的中点连接起来,组成第2个三角形,第2个三角形占原来三角形面积的;再把这个三角形的中点连接起来,组成第3个三角形,第3个三角形又占刚刚画出的第2个三角形的,也就是占原来大三角形的×=;再把这个三角形的中点连接起来,组成第4个三角形,第4个三角形又占刚刚画出的第3个三角形的,也就是占原来大三角形的×=;再把这个三角形的中点连接起来,组成第5个三角形,第5个三角形又占刚刚画出的第4个三角形的,也就是占原来大三角形的×= 已知最大三角形的面积是2平方分米,÷2=,据此可知第5个三角形的面积是平方分米,据此解答即可。
【详解】÷2=
又因为第5个三角形占原来大三角形的,所以第5个三角形的面积是平方分米。
【点睛】本题考查了数与形的组合知识,结合题意分析解答即可。
10.n2+1
【分析】观察数列可知,2=12+1,5=22+1,10=32+1,17=42+1,26=52+1,则第n个数是n2+1。
【详解】由分析可知:
2、5、10、17、26、37…第n个数是n2+1。
【点睛】本题考查数字的排列规律,发现规律,利用规律是解题的关键。
11. 37 4n-3
【分析】根据题意,第1幅图的点数为1+4×0,第2幅图的点数为1+4×1,第3幅图的点数为1+4×2;第4幅图的点数为1+4×3,那么第n幅图的点数应为:1+4(n-1)=4n-3;将n=10,代入计算出第10幅图即可;据此解答。
【详解】根据分析,第n幅图的点数应为:4n-3;
当n=10时,4×10-3=37
所以,依次排下去,第10幅图的点数为37,第n幅图的点数为4n-3。
【点睛】此题考查了数与形的知识,关键能够根据增加数量找出规律再解答。
12.24
【分析】观察图形可知,第1个图形的周长为8cm,第2个图形的周长为12cm,第3个图形的周长为16cm,由此可知相邻的两个图形之间的周长的差为4,则第4个图形的周长为16+4=20cm,第5个图形的周长为20+4=24cm。
【详解】16+4=20(cm)
20+4=24(cm)
则第(5)个图形的周长是24cm。
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
13. 15 3n
【分析】观察图形得到第1个图形所需棋子数=3×2-3=3×1
第2个图形所需棋子数=3×3-3=6=3×2
第3个图形所需棋子数=3×4-3=9=3×3
所以得到图形中棋子的个数等于该图的序号数的3倍;
则第4个图形所需棋子数=3×4
第5个图形所需棋子数=3×5=15
第n个图形所需棋子数=3n,据此解答。
【详解】由分析可得:
3×5=15(颗)
3×n=(3n)颗
摆第5个图形需15颗★。像这样,摆第n个图形需要(3n)颗★。
【点睛】本题考查了数与形的规律知识,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,根据规律解答即可。
14. 12
【分析】观察图形,摆第1幅图需要4个〇,摆第2幅图需要(4+2)个〇,摆第3幅图需要(4+2×2)个〇,可见,当前图形中〇的个数比前一个图形中〇的个数多2个,依次类推,算出摆第5幅图需要多少个〇。继而求出摆第n幅图需要个〇。
【详解】根据分析得,
4+2×(5-1)
=4+2×4
=4+8
=12(个)
=4+2×n-2×1
=4-2+2n
=(2n+2)个
即摆第5幅图需要12个〇;摆第n幅图需要(2n+2)个〇。
【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
15.(1)边长是10厘米的正方形画框。
(2)取1厘米与8厘米连接、取2厘米与7厘米连接、取3厘米与6厘米连接、取9厘米的木条依次连接即可做出。
【分析】根据题意,9根细木条可以连接成边长为10厘米的正方形或边长为9厘米的正方形,利用整数加法的运算法则计算即可。
【详解】(1)根据题意:
1+9=10(厘米)
2+8=10(厘米)
3+7=10(厘米)
4+6=10(厘米)
答:小兔可以做边长是10厘米的正方形画框。(答案不唯一,合理即可。)
(2)要做边长是9厘米的正方形的画框:
1+8=9(厘米)
2+7=9(厘米)
3+6=9(厘米)
最后取9厘米的木条。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
16.42人;9张
【详解】9×4+6=42(人)
38-10=28(人)
28÷4=7(张)
7+2=9(张)
答:并成一排可以坐42人;如果一共有38人,需要并9张桌子才能坐下。
17.45根
【详解】9×(9+1)÷2 = 45(根)
18.36=15+21
【详解】题目中“三角形数”的规律为1、3、6、10、15、21…“正方形数”的规律为1、4、9、16、25…,根据题目已知条件:从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.可得出最后结果 .
19.(1)76个
(2)49,50
【详解】(1)观察图形可得
第1个图形中有个4+1×2=6小圆点
第2个图形中有4+2×3=10个小圆点
第3个图形中有4+3×4=16个小圆点
第4个图形中有4+4×5=24个小圆点
通过总结可得,第8个图形有4+8×9=76个小圆点:
(2)第n个图形中,小圆点的个数为:4+n(n+1)=(n +n+4)个.
第n-1个图形中,小圆点的个数为:4+(n-1)n=(n -n+4)个.
它们的差是:2n=100,所以n=50
所以这两个图形分别是第50个和第49个图形.
20.(1)12;16;20;24 (2) 16块 (3) (4n+4)块
【详解】(2)(20÷4-1)×(20÷4-1)=16(块)
答:白瓷砖用了16块。
(3)n2=n×n,(n+1)×4=4n+4(块)。
答:花瓷砖用了(4n+4)块。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八单元数学广角-数与形易错题大集结-数学六年级上册人教版
一、选择题
1.按规律摆六边形,如果摆n个六边形,需要( )根小棒。
A.6n B. C.
2.如图所示,用黑白两种颜色的正五边形地砖按下图所示的规律,拼成若干个蝴蝶图案,则第7个蝴蝶图案中白色地砖有( )。
A.35块 B.27块 C.22块 D.7块
3.小蚂蚁从O点出发,围绕一块扇形奶酪爬一周(如图)。下面( )幅图描述了它的活动行程。
A. B.
C. D.
4.过2个点可以画出1条线段,过3个点可以画3条线段,过10个点可以画( )条线段。
A.10 B.54 C.45 D.无数条
5.观察下边图形,按此规律,第⑩个图中○的个数有( )个。
A.55 B.40 C.36 D.10
6.正方形纸片按规律拼成如下的图案,第( )个图案中恰好有365个纸片。
A.73 B.81 C.91
二、填空题
7.林林用火柴棒在桌面上摆图形(如图),已经摆了3个正方形。照这样继续摆下去,要摆出6个正方形,一共需要( )根火柴棒。
8.根据图形中各个数的关系,★=( ),▲=( )。
9.如下图,先把三角形各边的中点连接起来,组成第2个三角形。再把这个三角形的中点连接起来,组成第3个三角形……已知最大三角形的面积是2平方分米,第( )个三角形的面积是平方分米。
10.按规律填空:2、5、10、17、26、37…第n个数是( )。
11.古希腊著名的毕达哥拉斯学派经常把“形”与“数”联系在一起,下图是用“形”来表示“数”、请你认真观察:第1幅图的点数为1,第2幅图的点数为5,第3幅图的点数为9,依次排下去,第10幅图的点数为( ),第n幅图的点数为( )。
12.4个边长为1cm小正方形组成图形。下面这一列图形由重叠而成。按这样的方式重叠,第(5)个图形的周长是( )cm。
13.牛牛摆“星星”如图所示,摆第1个图形需3颗★,摆第2个图形需6颗★,……,摆第5个图形需( )颗★。像这样,摆第n个图形需要( )颗★。
14.用黑、白两种颜色的圆摆图形。
……
像这样继续摆下去,摆第5幅图需要( )个〇;摆第n幅图需要( )个〇。
三、解答题
15.小兔想做一个正方形的画框,可是它的细木条长短都不一样,有1,2,3,4,5,6,7,8,9厘米长的细木条各一根.
(1)如果不能锯断,但可以连接(接头处不计损耗),小兔可以做一个怎样的正方形画框?
(2)要做边长是9厘米的正方形的画框,可以怎么做?
16.一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人,照这样,10张桌子并成一排可以坐多少人?如果一共有38人,需要并多少张桌子才能坐下?
17.按照右边的方法堆木头,如果底层放9根木头,完成堆放后,木头的总根数是多少根?
18.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.请写出第5个图形的算式.
4=1+3 9=3+6 16=6+10
19.将一些小圆点按一定的规律摆放,所得到的图形依次为第1个图形、第2个图形、第3个图形、第4个图形.如下图所示,各个图形的小圆点个数依次是6个、10个、16个、24个……
第1个图形 第2个图形 第3个图形 第4个图形
(1)第8个图形一共有多少个小圆点
(2)已知连续两个图形的小圆点的个数差是100个.这两个图形分别是第个______图形和第个______图形.
20.用花、白两种正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用花瓷砖(如图所示)。
(1)填写下列表格。
大正方形每边的瓷砖块数 3 4 5 6 7 …
花瓷砖块数 8 …
(2)如果所拼的图形中,用了20块花瓷砖,那么白瓷砖用了多少块?
(3)如果所拼的图形中,用了n2块白瓷砖,那么花瓷砖用了多少块?
参考答案:
1.B
【分析】观察可知,小棒数量=六边形数量×5+1,据此分析。
【详解】n×5+1=5n+1=1+5n
故答案为:B
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
2.C
【分析】观察图形,第1个图形白色砖的数量是:4=3+1;
第2个图形白色砖的数量是:7=3×2+1;
第3个图形白色砖的数量是:10=3×3+1;
可以得出规律:第n个蝴蝶图案中白色地砖有块;据此解答。
【详解】由分析可知,第n个蝴蝶图案中白色地砖有块,
当时,白色地砖数量为3×7+1=22(块)。
【点睛】此题考查了数与形的规律问题,关键是结合图形数量之间的运算关系,找出规律即可。
3.B
【分析】一只蚂蚁从O点出发,沿着扇形的边缘匀速爬行,在开始时经过第一段时,蚂蚁到O点的距离随运动时间t的增大而增大;到第二段弧形这段路程时,蚂蚁到O点的距离S不变,到第三段时,走的是另一条半径,蚂蚁到O点的距离随运动时间t的增大而减小。据此解答。
【详解】A.第三段路程随着时间的增大还在增大,不符合题意;
B.第一段随着时间的增大,路程也在增大,第二段路程不变,第三段随着时间的增加,路程在减小。符合题意;
C.第三段路程在减少,时间却不变,显然不符合题意;
D.只有第一段和第三段路程的表述,第二段路程不变并没有在图形中体现出来,不符合题意;
故答案为:B
【点睛】根据蚂蚁在扇形上运动时,随着时间的变化,距离不断发生变化,从而得出图像的特点,即可得出结论。
4.C
【分析】如图:
2个点,1条线段;
3个点,3条线段,3=3×2÷2;
4个点,6条线段,6=4×3÷2;
5个点,10条线段,10=5×4÷2;
……
规律:点的个数为n(n≥2),可以画的线段为:条;
据此规律,得出过10个点可以画的线段的条数。
【详解】规律:点的个数为n(n≥2),可以画的线段为:条;
n=10时
=
(条)
过10个点可以画45条线段。
故答案为:C
【点睛】本题是找规律的题型,通过画图发现点数与线段的规律,利用规律解答。
5.A
【分析】第几个图中就有几层,且每层圆的个数与层数相同,据此把各层圆的个数进行求和解答。
【详解】图①中圆的个数:1=1
图②中圆的个数:3=1+2
图③中圆的个数:6=1+2+3
图④中圆的个数:10=1+2+3+4
……
图⑩中圆的个数:55=1+2+3+4+……+10
故答案为:A
【点睛】本题考查运用数形结合的方法探究数学规律,注意要把图形和数一一对应。
6.C
【分析】由题干可知,第1个图案中有纸片的个数:5=1+4×1;
第2个图案中有纸片的个数:9=1+4×2;
第3个图案中有纸片的个数:13=1+4×3;
……
第n个图案中有纸片的个数:4n+1,据此解答。
【详解】(365-1)÷4
=364÷4
=91(个)
所以第91个图案中恰好有365个纸片。
故答案为:C
【点睛】此题考查的是找规律,正确找出规律并用规律解决问题是解题关键。
7.19
【分析】摆1个正方形需要4根火柴棒,每增加1个正方形,需要增加3根火柴棒。则摆2个正方形需要(4+3)根火柴棒,摆3个正方形需要(4+2×3)根火柴棒。摆6个正方形需要(4+5×3)根火柴棒。据此解答。
【详解】4+(6-1)×3
=4+5×3
=4+15
=19(根)
一共需要19根火柴棒。
【点睛】解决本题的关键是明确正方形个数与火柴棒根数之间的关系,再根据这个关系解决问题。
8. 26 32
【分析】由图分析可知,黑色三角形位置的数字是16的2倍,五角星星位置的数字是比16多10。
【详解】★=16+10=26
▲=16×2=32
【点睛】此题考查学生的观察推理能力。
9.5
【分析】根据题意,先把三角形各边的中点连接起来,组成第2个三角形,第2个三角形占原来三角形面积的;再把这个三角形的中点连接起来,组成第3个三角形,第3个三角形又占刚刚画出的第2个三角形的,也就是占原来大三角形的×=;再把这个三角形的中点连接起来,组成第4个三角形,第4个三角形又占刚刚画出的第3个三角形的,也就是占原来大三角形的×=;再把这个三角形的中点连接起来,组成第5个三角形,第5个三角形又占刚刚画出的第4个三角形的,也就是占原来大三角形的×= 已知最大三角形的面积是2平方分米,÷2=,据此可知第5个三角形的面积是平方分米,据此解答即可。
【详解】÷2=
又因为第5个三角形占原来大三角形的,所以第5个三角形的面积是平方分米。
【点睛】本题考查了数与形的组合知识,结合题意分析解答即可。
10.n2+1
【分析】观察数列可知,2=12+1,5=22+1,10=32+1,17=42+1,26=52+1,则第n个数是n2+1。
【详解】由分析可知:
2、5、10、17、26、37…第n个数是n2+1。
【点睛】本题考查数字的排列规律,发现规律,利用规律是解题的关键。
11. 37 4n-3
【分析】根据题意,第1幅图的点数为1+4×0,第2幅图的点数为1+4×1,第3幅图的点数为1+4×2;第4幅图的点数为1+4×3,那么第n幅图的点数应为:1+4(n-1)=4n-3;将n=10,代入计算出第10幅图即可;据此解答。
【详解】根据分析,第n幅图的点数应为:4n-3;
当n=10时,4×10-3=37
所以,依次排下去,第10幅图的点数为37,第n幅图的点数为4n-3。
【点睛】此题考查了数与形的知识,关键能够根据增加数量找出规律再解答。
12.24
【分析】观察图形可知,第1个图形的周长为8cm,第2个图形的周长为12cm,第3个图形的周长为16cm,由此可知相邻的两个图形之间的周长的差为4,则第4个图形的周长为16+4=20cm,第5个图形的周长为20+4=24cm。
【详解】16+4=20(cm)
20+4=24(cm)
则第(5)个图形的周长是24cm。
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
13. 15 3n
【分析】观察图形得到第1个图形所需棋子数=3×2-3=3×1
第2个图形所需棋子数=3×3-3=6=3×2
第3个图形所需棋子数=3×4-3=9=3×3
所以得到图形中棋子的个数等于该图的序号数的3倍;
则第4个图形所需棋子数=3×4
第5个图形所需棋子数=3×5=15
第n个图形所需棋子数=3n,据此解答。
【详解】由分析可得:
3×5=15(颗)
3×n=(3n)颗
摆第5个图形需15颗★。像这样,摆第n个图形需要(3n)颗★。
【点睛】本题考查了数与形的规律知识,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,根据规律解答即可。
14. 12
【分析】观察图形,摆第1幅图需要4个〇,摆第2幅图需要(4+2)个〇,摆第3幅图需要(4+2×2)个〇,可见,当前图形中〇的个数比前一个图形中〇的个数多2个,依次类推,算出摆第5幅图需要多少个〇。继而求出摆第n幅图需要个〇。
【详解】根据分析得,
4+2×(5-1)
=4+2×4
=4+8
=12(个)
=4+2×n-2×1
=4-2+2n
=(2n+2)个
即摆第5幅图需要12个〇;摆第n幅图需要(2n+2)个〇。
【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
15.(1)边长是10厘米的正方形画框。
(2)取1厘米与8厘米连接、取2厘米与7厘米连接、取3厘米与6厘米连接、取9厘米的木条依次连接即可做出。
【分析】根据题意,9根细木条可以连接成边长为10厘米的正方形或边长为9厘米的正方形,利用整数加法的运算法则计算即可。
【详解】(1)根据题意:
1+9=10(厘米)
2+8=10(厘米)
3+7=10(厘米)
4+6=10(厘米)
答:小兔可以做边长是10厘米的正方形画框。(答案不唯一,合理即可。)
(2)要做边长是9厘米的正方形的画框:
1+8=9(厘米)
2+7=9(厘米)
3+6=9(厘米)
最后取9厘米的木条。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
16.42人;9张
【详解】9×4+6=42(人)
38-10=28(人)
28÷4=7(张)
7+2=9(张)
答:并成一排可以坐42人;如果一共有38人,需要并9张桌子才能坐下。
17.45根
【详解】9×(9+1)÷2 = 45(根)
18.36=15+21
【详解】题目中“三角形数”的规律为1、3、6、10、15、21…“正方形数”的规律为1、4、9、16、25…,根据题目已知条件:从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.可得出最后结果 .
19.(1)76个
(2)49,50
【详解】(1)观察图形可得
第1个图形中有个4+1×2=6小圆点
第2个图形中有4+2×3=10个小圆点
第3个图形中有4+3×4=16个小圆点
第4个图形中有4+4×5=24个小圆点
通过总结可得,第8个图形有4+8×9=76个小圆点:
(2)第n个图形中,小圆点的个数为:4+n(n+1)=(n +n+4)个.
第n-1个图形中,小圆点的个数为:4+(n-1)n=(n -n+4)个.
它们的差是:2n=100,所以n=50
所以这两个图形分别是第50个和第49个图形.
20.(1)12;16;20;24 (2) 16块 (3) (4n+4)块
【详解】(2)(20÷4-1)×(20÷4-1)=16(块)
答:白瓷砖用了16块。
(3)n2=n×n,(n+1)×4=4n+4(块)。
答:花瓷砖用了(4n+4)块。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
