多边形的内角和(浙江省台州市)
文档属性
| 名称 | 多边形的内角和(浙江省台州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 282.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-03 00:00:00 | ||
图片预览




文档简介
课件19张PPT。§7.3.2多边形的内角和0101222353494514n-3n-21.多边形的定义;2.多边形的边数与对角线的关系:复习巩固巩固复习问题3:
三角形的内角和、外角和分别是多少? 问题4:
长方形、正方形的内角和分别是多少? 问题5:
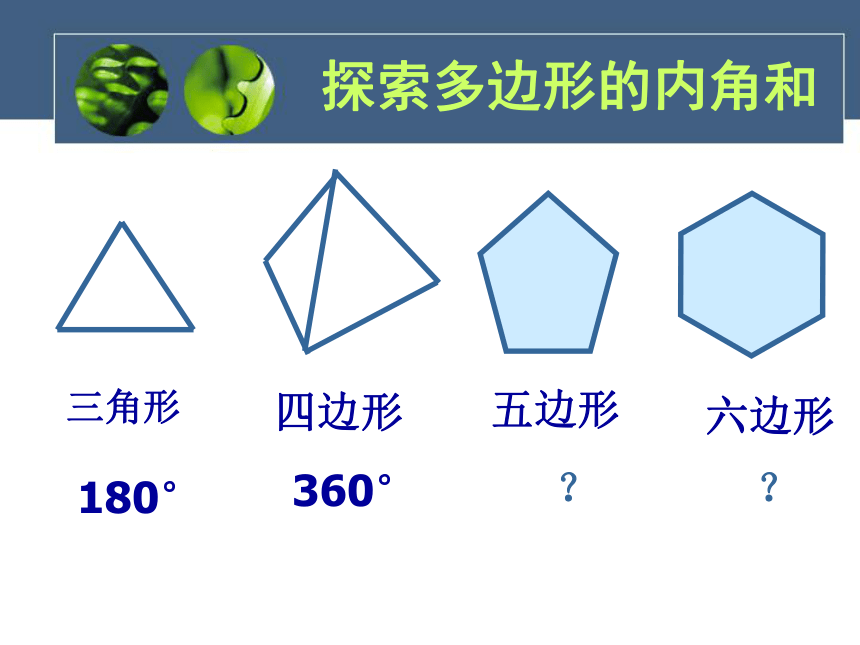
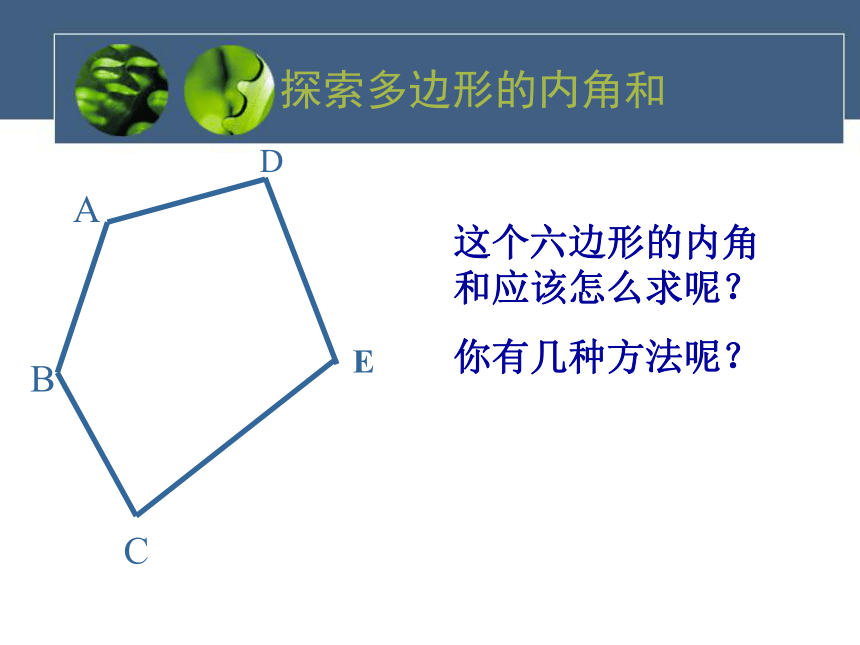
四边形的内角和是多少?四边形内角和为3600三角形 六边形 四边形探索多边形的内角和五边形180°360°??探索多边形的内角和这个六边形的内角和应该怎么求呢?
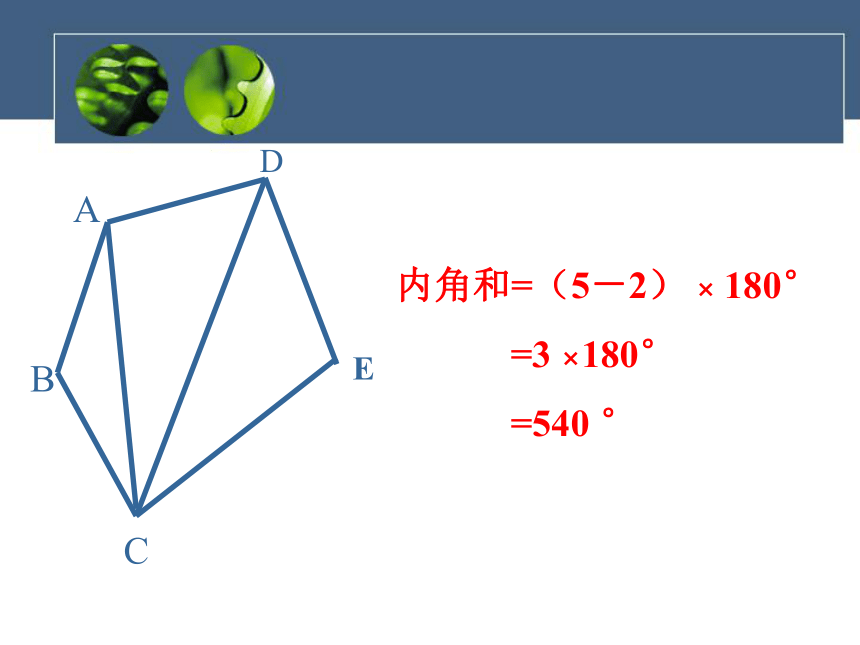
你有几种方法呢?ACDEB内角和=(5-2) × 180°
=3 ×180°
=540 °ACDEBO内角和=4×180°-180°
= 3×180°
=540°ACDEBO内角和=5×180°-360 °
=3×180°
=540 °探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °(n-2) ×1800720 °540 °n 边形的内角和为:(n-2)×180°总结n边形内角和为(n-2)×1800五边形180°360°540°n边形1.快速抢答 (1)8边形内角和是 . (2)32边形内角和是 . (3)一个多边形的内角和是1440°, 它是_____边形。应用知识解决问题(1)105400°1080°2.多边形外角与相邻内角之间有什么关系?
应用知识解决问题(1)(1)各内角与相邻外角互补;(2)外角和=n个平角-内角和
=n×180°-(n-2) × 180°=360°(3)结论:n边形的外角和等于360°一.选择
1.一个多边形的内角和为1800°,则它的边数为( )
A 10 B 12 C 8 D 15
2.n多边形的每一个外角是36°,则n是( )
A 4 B 5 C 8 D 10
3.多边形的每一个内角都等于150°,则从此多边形一个顶点出发引出的对角线有( )
A 7条 B 8条 C 9条 D 10条课堂练习BDC
4. 如果把一个多边形的边数增加1倍,它的内角和是2160°,那么原来的多边形的边数是( )
A 5 B 6 C 7 D 8
5.如果一个多边形的边数增加1,则它的内角和将( )
A增加90° B增加180° C 增加360° D不变BB二、解答题
6、一个多边形的内角和是外角和的k倍,
求这个n边形的边数。
7、多边形的内角和与某一个外角的度数
总和为1350°,求这个n边形的边数。探究 小明想:2008年奥运会在北京召开,设计一个内角和为2008?的多边形图案多有意义,小明的想法能实现吗?探索研究 由三角形内角和推广到多边形内角和并且用于解决问题十分重要, n边形内角和等于(n-2)个平角,既(n-2)·180°,边数增加,内角和也增加,边数减少,内角和也减少,边数每增加(减少)1,内角和就增加(减少)180°。n边形外角和等于360°,与边数无关。它有鲜明的直观意义,设想一辆汽车在多边形的边界上绕圈子(如图一),每经过一个顶点,前进的方向就
要改变一次,改变的角度恰好是
这个顶点处的外角,绕了一圈,
回到原处,方向与当初出发时一
致了,角度的改变量之和当然是360°。
课时小结通过本节课的学习,你学到了哪些知识?有何体会?(1)这节课我们主要学习了多边形的内角和公式:(n-2)×180?;
(2)多边形的外角和为:3600
三角形的内角和、外角和分别是多少? 问题4:
长方形、正方形的内角和分别是多少? 问题5:
四边形的内角和是多少?四边形内角和为3600三角形 六边形 四边形探索多边形的内角和五边形180°360°??探索多边形的内角和这个六边形的内角和应该怎么求呢?
你有几种方法呢?ACDEB内角和=(5-2) × 180°
=3 ×180°
=540 °ACDEBO内角和=4×180°-180°
= 3×180°
=540°ACDEBO内角和=5×180°-360 °
=3×180°
=540 °探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °(n-2) ×1800720 °540 °n 边形的内角和为:(n-2)×180°总结n边形内角和为(n-2)×1800五边形180°360°540°n边形1.快速抢答 (1)8边形内角和是 . (2)32边形内角和是 . (3)一个多边形的内角和是1440°, 它是_____边形。应用知识解决问题(1)105400°1080°2.多边形外角与相邻内角之间有什么关系?
应用知识解决问题(1)(1)各内角与相邻外角互补;(2)外角和=n个平角-内角和
=n×180°-(n-2) × 180°=360°(3)结论:n边形的外角和等于360°一.选择
1.一个多边形的内角和为1800°,则它的边数为( )
A 10 B 12 C 8 D 15
2.n多边形的每一个外角是36°,则n是( )
A 4 B 5 C 8 D 10
3.多边形的每一个内角都等于150°,则从此多边形一个顶点出发引出的对角线有( )
A 7条 B 8条 C 9条 D 10条课堂练习BDC
4. 如果把一个多边形的边数增加1倍,它的内角和是2160°,那么原来的多边形的边数是( )
A 5 B 6 C 7 D 8
5.如果一个多边形的边数增加1,则它的内角和将( )
A增加90° B增加180° C 增加360° D不变BB二、解答题
6、一个多边形的内角和是外角和的k倍,
求这个n边形的边数。
7、多边形的内角和与某一个外角的度数
总和为1350°,求这个n边形的边数。探究 小明想:2008年奥运会在北京召开,设计一个内角和为2008?的多边形图案多有意义,小明的想法能实现吗?探索研究 由三角形内角和推广到多边形内角和并且用于解决问题十分重要, n边形内角和等于(n-2)个平角,既(n-2)·180°,边数增加,内角和也增加,边数减少,内角和也减少,边数每增加(减少)1,内角和就增加(减少)180°。n边形外角和等于360°,与边数无关。它有鲜明的直观意义,设想一辆汽车在多边形的边界上绕圈子(如图一),每经过一个顶点,前进的方向就
要改变一次,改变的角度恰好是
这个顶点处的外角,绕了一圈,
回到原处,方向与当初出发时一
致了,角度的改变量之和当然是360°。
课时小结通过本节课的学习,你学到了哪些知识?有何体会?(1)这节课我们主要学习了多边形的内角和公式:(n-2)×180?;
(2)多边形的外角和为:3600
