湖南省衡阳市2023-2024学年八年级上学期第一次月考数学试题(含答案)
文档属性
| 名称 | 湖南省衡阳市2023-2024学年八年级上学期第一次月考数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 697.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 00:00:00 | ||
图片预览



文档简介
2023年10月九中第一次月考试卷
八年级数学
时量:120分钟 总分:120分
一、选择题(共12小题)
1.若二次根式在实数范围内有意义,则的取值范围是( )
A. B. C. D.
2.在中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
3.下列说法中:①3的平方根是;②是9的一个平方根;③的平方根是;④0.01的算术平方根是0.1;⑤;⑥的立方根是2;其中正觕的有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法中,正确的个数是( )
①实数包括有理数、无理数和0;②有理数和数轴上的点一一对应;(3)无理数都是无限小数;④;⑤平方根与立方根都等于它本身的数为0利1;
A.1个 B.2个 C.3个 D.4个
5.已知,则的值为( )
A.72 B.54 C.17 D.12
6.在边长为a的正方形中挖去一个边长为6的小正方形()(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
A. B.
C. D.
7.已知,则的值为( )
A. B. C.1 D.5
8.计算的结果是( )
A. B.2 C. D.
9.已知,则的值为是( )
A.7 B.8 C.9 D.12
10.在数学中,为了书写简便,18世纪数学家欧拉就引进了求和符号“”,如记;
已知,则的值是( )
A. B. C. D.
11.如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数,恰好对应展开式中各项的系数;第四行的四个数恰好对应着的系数.根据数表中前四行的数字所反映的规律计算求值:( )
A. B. C. D.
12.已知图①是长为,宽为的小长方形纸片,图②是大长方形,且边,将7张如图①的小长方形纸片不重叠地放在大长方形内,如图③所示,未被覆盖两个长方形用阴影表示.设左上角与右下角的阴影部分的面积差为,若的长度变化时,始终保持不变,则应满足( )
A. B. C. D.
二、填空题(共6小题)
13.的平方根是__________.
14.一个正数的两个平方根分别是和,则这个正数是__________.
15.,则__________.
16.已知的展开式中不含和项,则__________.
17.若关于的二次三项式是完全平方式,则的值为__________.
18.任何实数,可用表示不超过的最大整数,如.现对72进行如下操作:72第一次,第二次,第三次,类似地,只需进行3次操作变为1的所有正整数中,最大的是__________.
三、解答题(共8小题)
19.计算:;
20.化简求值:,其中.
21.尝试解决下列有关幂的问题:
(1)若,求的值;
(2)已知,求的值;
(3)若为正整数,且,求的值.
22.定义一种新运算:观察下列各式:
(Ⅰ)请计算__________;
(Ⅱ)请猜一猜:__________.(用含的代数式表示);
(Ⅲ)若,请计算的值.
23.上数学课时,老师在讲完乘法公式的多种运用后,要求同学们运用所学知识解答:求代数式的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
解:
,
当时,的值最小,最小值是0,
.
当时,的值最小,最小值是1,
的最小值是1.
请你根据上述方法,解答下列各题:
(1)知识再现:当__________时,代数式有最小值是__________;
(2)知识运用:若,求的最大值;
(3)知识拓展:若,求的最小值.
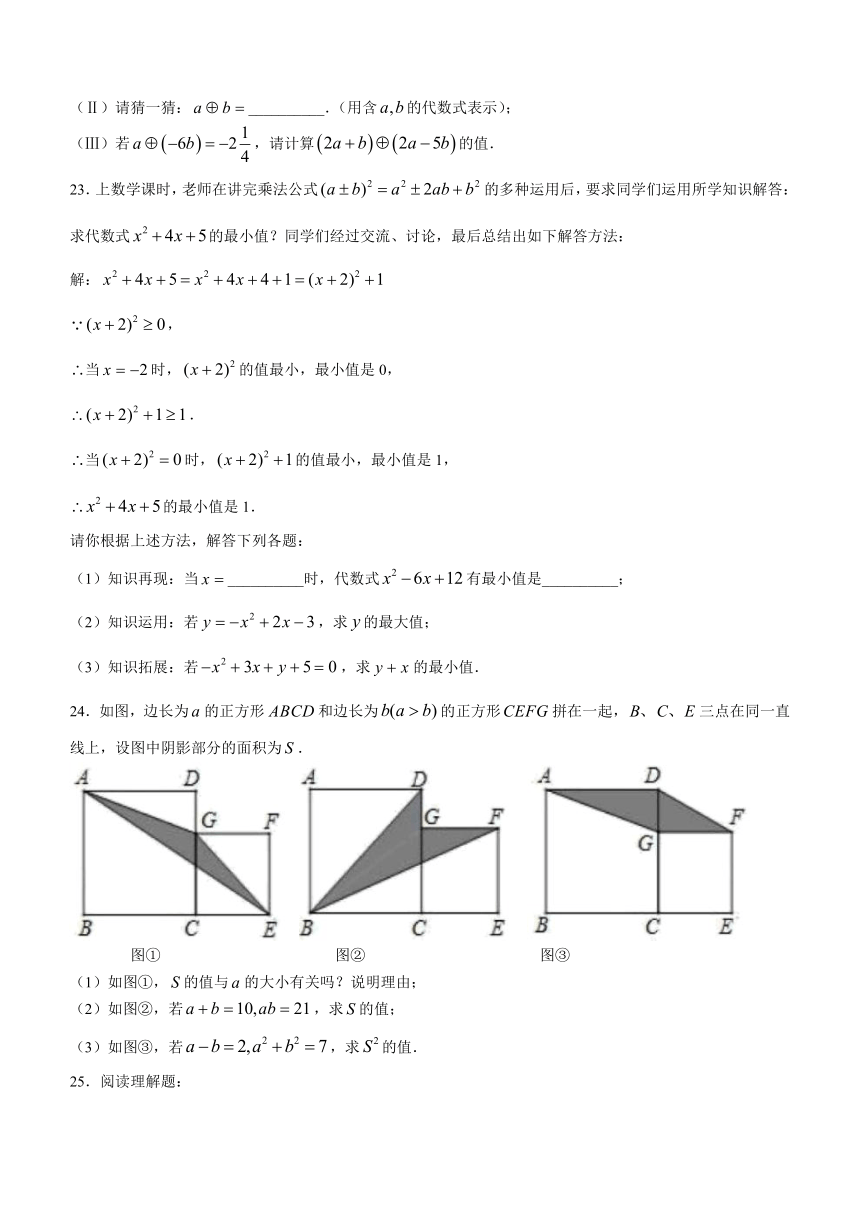
24.如图,边长为的正方形和边长为的正方形拼在一起,三点在同一直线上,设图中阴影部分的面积为.
图① 图② 图③
(1)如图①,的值与的大小有关吗?说明理由;
(2)如图②,若,求的值;
(3)如图③,若,求的值.
25.阅读理解题:
定义:如果一个数的平方等于,记为,这个数叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为为实数叫这个复数的实部,叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:.
(1)填空:__________,__________.
(2)计算:①;②;
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知:,(为实数),求的值.
(4)试一试:请利用以前学习的有关知识将化简成的形式.
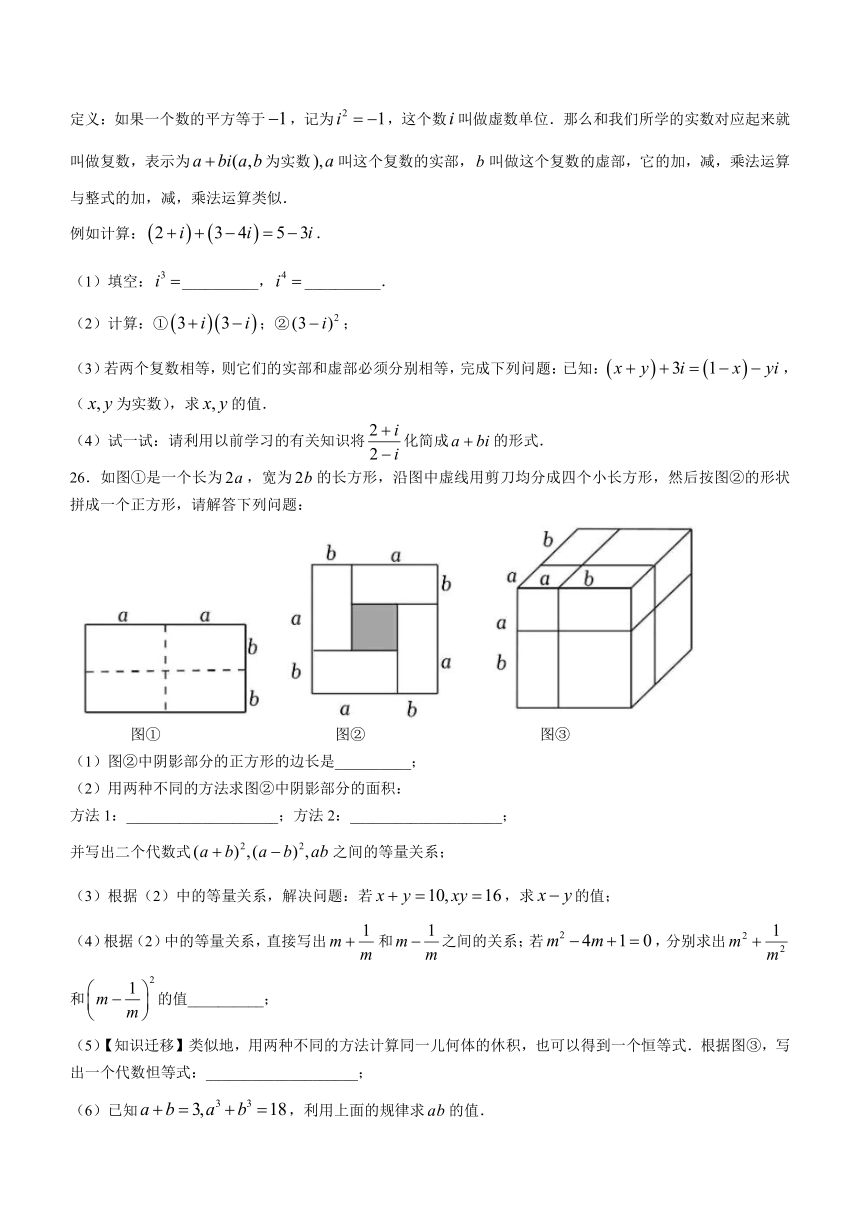
26.如图①是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形,请解答下列问题:
图① 图② 图③
(1)图②中阴影部分的正方形的边长是__________;
(2)用两种不同的方法求图②中阴影部分的面积:
方法1:____________________;方法2:____________________;
并写出二个代数式之间的等量关系;
(3)根据(2)中的等量关系,解决问题:若,求的值;
(4)根据(2)中的等量关系,直接写出和之间的关系;若,分别求出和的值__________;
(5)【知识迁移】类似地,用两种不同的方法计算同一儿何体的休积,也可以得到一个恒等式.根据图③,写出一个代数怛等式:____________________;
(6)已知,利用上面的规律求的值.
八年级数学
参考答案
一、选择题(共12小题)
1.【考点】平方根的概念
【解答】B
2.【考点】无理数的定义
【解答】D
3.【考点】平方根、立方根
【解答】C
4.【考点】实数的概念
【解答】A
5.【考点】幂运算
【解答】A
6.【考点】乘法公式的几何意义
【解答】C
7.【考点】多项式乘多项式
【解答】A
8.【考点】幂运算
【解答】C
9.【考点】整式乘法
【解答】C
10.【考点】乘方
【解答】B
11.【考点】完全平方公式、找规律
【解答】A
12.【考点】整式的混合运算
【解答】D
解:如图,左上角阴影部分的长为,宽为,右下角阴影部分的长为,宽为,阴影部分面积之差,
则,即.
二、填空题(共6小题)
13.【考点】平方根、算术平方根、
【解答】解:的平方根是,故答案为:
14.【考点】平方根
【解答】解:一个正数的两个平方根分别是和,
,
,
,
这个正数为,
故答案为:49.
15.【考点】平方差公式
【解答】解:设
则,
.
故答案为:9
16.【考点】多项式乘多项式
【解答】解:,的展开式中不含和项,
则有,
解得:,
故答案为:10.
17.【考点】完全平方式
【解答】解:二次三项式是完全平方式,
或.
故答案为:或.
18.【考点】实数大小比较;算术平方根
【解答】解:,
而:,
即:只需进行3次操作后变为1的所有正整数中,最大的是:255,故答案为:255.
三、解答题(共8小题)
19.【考点】有理数的混合运算
【解答】解:
20.【考点】整式的混合运算-化简求值
【解答】解:原式
,
原式
21.【考点】幂运算
【解答】解:(1)原式
即,则,
即.
(2).
(3)原式
22.【考点】有理数的混合运算,代数式
【解答】解:(Ⅰ)
故答案为:,
(Ⅱ),
故答案为:.
(Ⅲ)当时,
即:,
23.【考点】配方求最值
【解答】解:(1),当时,代数式有最小值3;故答案为:3,3;
(2),
当时,有最大值.
即有最大值,此时;
(3),
当时,的最小值为.
24.【考点】完全平方公式的几何运用
【解答】解:(1)S的值与a无关,理由如下:
由题意知:,
的值与无关.
(2),
.
(3),
.
,
,
,
,
,
25.【考点】实数的运算;找规律
【解答】解:(1),
,,
(2)①;
②;
(3),
,
;
(4)
26.【考点】完全平方公式的几何应用,化简求值
【解答】解:(1)由题意可得小矩形的长为,宽为,
图2中阴影部分正方形的边长为:,
故答案为:;
(2)阴影部分的面积:
方法一:利用整体思想,边长为的正方形其面积为,
方法二:利用分割思想,阴影部分面积边长为的大正方形面积个长为宽为的矩形面积,
三个代数式之间的数量关系为:,
或:;
(3),且,
,
;
(4)由(2)可得:,
,,
,
,
综上,的值为的值为12.
(5)方法一:正方体棱长为
体积为,
方法二:正方体体积是长方体和小正方体的体积和,即,
故答案为:;
(6),
.
八年级数学
时量:120分钟 总分:120分
一、选择题(共12小题)
1.若二次根式在实数范围内有意义,则的取值范围是( )
A. B. C. D.
2.在中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
3.下列说法中:①3的平方根是;②是9的一个平方根;③的平方根是;④0.01的算术平方根是0.1;⑤;⑥的立方根是2;其中正觕的有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法中,正确的个数是( )
①实数包括有理数、无理数和0;②有理数和数轴上的点一一对应;(3)无理数都是无限小数;④;⑤平方根与立方根都等于它本身的数为0利1;
A.1个 B.2个 C.3个 D.4个
5.已知,则的值为( )
A.72 B.54 C.17 D.12
6.在边长为a的正方形中挖去一个边长为6的小正方形()(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
A. B.
C. D.
7.已知,则的值为( )
A. B. C.1 D.5
8.计算的结果是( )
A. B.2 C. D.
9.已知,则的值为是( )
A.7 B.8 C.9 D.12
10.在数学中,为了书写简便,18世纪数学家欧拉就引进了求和符号“”,如记;
已知,则的值是( )
A. B. C. D.
11.如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数,恰好对应展开式中各项的系数;第四行的四个数恰好对应着的系数.根据数表中前四行的数字所反映的规律计算求值:( )
A. B. C. D.
12.已知图①是长为,宽为的小长方形纸片,图②是大长方形,且边,将7张如图①的小长方形纸片不重叠地放在大长方形内,如图③所示,未被覆盖两个长方形用阴影表示.设左上角与右下角的阴影部分的面积差为,若的长度变化时,始终保持不变,则应满足( )
A. B. C. D.
二、填空题(共6小题)
13.的平方根是__________.
14.一个正数的两个平方根分别是和,则这个正数是__________.
15.,则__________.
16.已知的展开式中不含和项,则__________.
17.若关于的二次三项式是完全平方式,则的值为__________.
18.任何实数,可用表示不超过的最大整数,如.现对72进行如下操作:72第一次,第二次,第三次,类似地,只需进行3次操作变为1的所有正整数中,最大的是__________.
三、解答题(共8小题)
19.计算:;
20.化简求值:,其中.
21.尝试解决下列有关幂的问题:
(1)若,求的值;
(2)已知,求的值;
(3)若为正整数,且,求的值.
22.定义一种新运算:观察下列各式:
(Ⅰ)请计算__________;
(Ⅱ)请猜一猜:__________.(用含的代数式表示);
(Ⅲ)若,请计算的值.
23.上数学课时,老师在讲完乘法公式的多种运用后,要求同学们运用所学知识解答:求代数式的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
解:
,
当时,的值最小,最小值是0,
.
当时,的值最小,最小值是1,
的最小值是1.
请你根据上述方法,解答下列各题:
(1)知识再现:当__________时,代数式有最小值是__________;
(2)知识运用:若,求的最大值;
(3)知识拓展:若,求的最小值.
24.如图,边长为的正方形和边长为的正方形拼在一起,三点在同一直线上,设图中阴影部分的面积为.
图① 图② 图③
(1)如图①,的值与的大小有关吗?说明理由;
(2)如图②,若,求的值;
(3)如图③,若,求的值.
25.阅读理解题:
定义:如果一个数的平方等于,记为,这个数叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为为实数叫这个复数的实部,叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:.
(1)填空:__________,__________.
(2)计算:①;②;
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知:,(为实数),求的值.
(4)试一试:请利用以前学习的有关知识将化简成的形式.
26.如图①是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形,请解答下列问题:
图① 图② 图③
(1)图②中阴影部分的正方形的边长是__________;
(2)用两种不同的方法求图②中阴影部分的面积:
方法1:____________________;方法2:____________________;
并写出二个代数式之间的等量关系;
(3)根据(2)中的等量关系,解决问题:若,求的值;
(4)根据(2)中的等量关系,直接写出和之间的关系;若,分别求出和的值__________;
(5)【知识迁移】类似地,用两种不同的方法计算同一儿何体的休积,也可以得到一个恒等式.根据图③,写出一个代数怛等式:____________________;
(6)已知,利用上面的规律求的值.
八年级数学
参考答案
一、选择题(共12小题)
1.【考点】平方根的概念
【解答】B
2.【考点】无理数的定义
【解答】D
3.【考点】平方根、立方根
【解答】C
4.【考点】实数的概念
【解答】A
5.【考点】幂运算
【解答】A
6.【考点】乘法公式的几何意义
【解答】C
7.【考点】多项式乘多项式
【解答】A
8.【考点】幂运算
【解答】C
9.【考点】整式乘法
【解答】C
10.【考点】乘方
【解答】B
11.【考点】完全平方公式、找规律
【解答】A
12.【考点】整式的混合运算
【解答】D
解:如图,左上角阴影部分的长为,宽为,右下角阴影部分的长为,宽为,阴影部分面积之差,
则,即.
二、填空题(共6小题)
13.【考点】平方根、算术平方根、
【解答】解:的平方根是,故答案为:
14.【考点】平方根
【解答】解:一个正数的两个平方根分别是和,
,
,
,
这个正数为,
故答案为:49.
15.【考点】平方差公式
【解答】解:设
则,
.
故答案为:9
16.【考点】多项式乘多项式
【解答】解:,的展开式中不含和项,
则有,
解得:,
故答案为:10.
17.【考点】完全平方式
【解答】解:二次三项式是完全平方式,
或.
故答案为:或.
18.【考点】实数大小比较;算术平方根
【解答】解:,
而:,
即:只需进行3次操作后变为1的所有正整数中,最大的是:255,故答案为:255.
三、解答题(共8小题)
19.【考点】有理数的混合运算
【解答】解:
20.【考点】整式的混合运算-化简求值
【解答】解:原式
,
原式
21.【考点】幂运算
【解答】解:(1)原式
即,则,
即.
(2).
(3)原式
22.【考点】有理数的混合运算,代数式
【解答】解:(Ⅰ)
故答案为:,
(Ⅱ),
故答案为:.
(Ⅲ)当时,
即:,
23.【考点】配方求最值
【解答】解:(1),当时,代数式有最小值3;故答案为:3,3;
(2),
当时,有最大值.
即有最大值,此时;
(3),
当时,的最小值为.
24.【考点】完全平方公式的几何运用
【解答】解:(1)S的值与a无关,理由如下:
由题意知:,
的值与无关.
(2),
.
(3),
.
,
,
,
,
,
25.【考点】实数的运算;找规律
【解答】解:(1),
,,
(2)①;
②;
(3),
,
;
(4)
26.【考点】完全平方公式的几何应用,化简求值
【解答】解:(1)由题意可得小矩形的长为,宽为,
图2中阴影部分正方形的边长为:,
故答案为:;
(2)阴影部分的面积:
方法一:利用整体思想,边长为的正方形其面积为,
方法二:利用分割思想,阴影部分面积边长为的大正方形面积个长为宽为的矩形面积,
三个代数式之间的数量关系为:,
或:;
(3),且,
,
;
(4)由(2)可得:,
,,
,
,
综上,的值为的值为12.
(5)方法一:正方体棱长为
体积为,
方法二:正方体体积是长方体和小正方体的体积和,即,
故答案为:;
(6),
.
同课章节目录
