第二十三章旋转 单元练习(含答案) 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十三章旋转 单元练习(含答案) 2023—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 302.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 20:59:56 | ||
图片预览


文档简介
第二十三章旋转 单元练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列图案中既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,如果点P1(a,﹣3)与点P2(4,b)关于原点O对称,那么式子(a+b)2018的值为( )
A.1 B.﹣1 C.2018 D.﹣2018
3.如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
A.(1,1) B.(0,1) C.(﹣1,1) D.(2,0)
4.如图,一个小孩坐在秋千上,若秋千绕点O旋转了80°,小孩的位置也从A点运动到了B点,则∠OAB的度数为 ( )
A.70° B.60° C.50° D.40°
5.如图,把 绕点 顺时针旋转35°得到 , , 交 于点 ,若 ,则 的度数为( )
A.25° B.35° C.45° D.55°
6.如图,将矩形绕点逆时针旋转得到矩形,已知,则旋转角的度数为( )
A. B. C. D.
7.如图,在平面直角坐标系中,点A(﹣1,m)在直线y=2x+3上,连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=﹣x+b上,则b的值为( )
A.-2 B.1 C. D.2
8.已知,矩形中,,,点是线段上的一个动点,将线段绕点逆时针旋转得到,过作于点,连接,取的中点,连接,.点在运动过程中,下列结论:①;②当点和点互相重合时,;③;④.正确的有( )个.
A.1 B.2 C.3 D.4
二、填空题:(本题共5小题,每小题3分,共15分.)
9.点P(2,-1)关于原点成中心对称的点Q的坐标是 .
10.如图,中,,,.将绕点A逆时针旋转60°,得到,连接,则 .
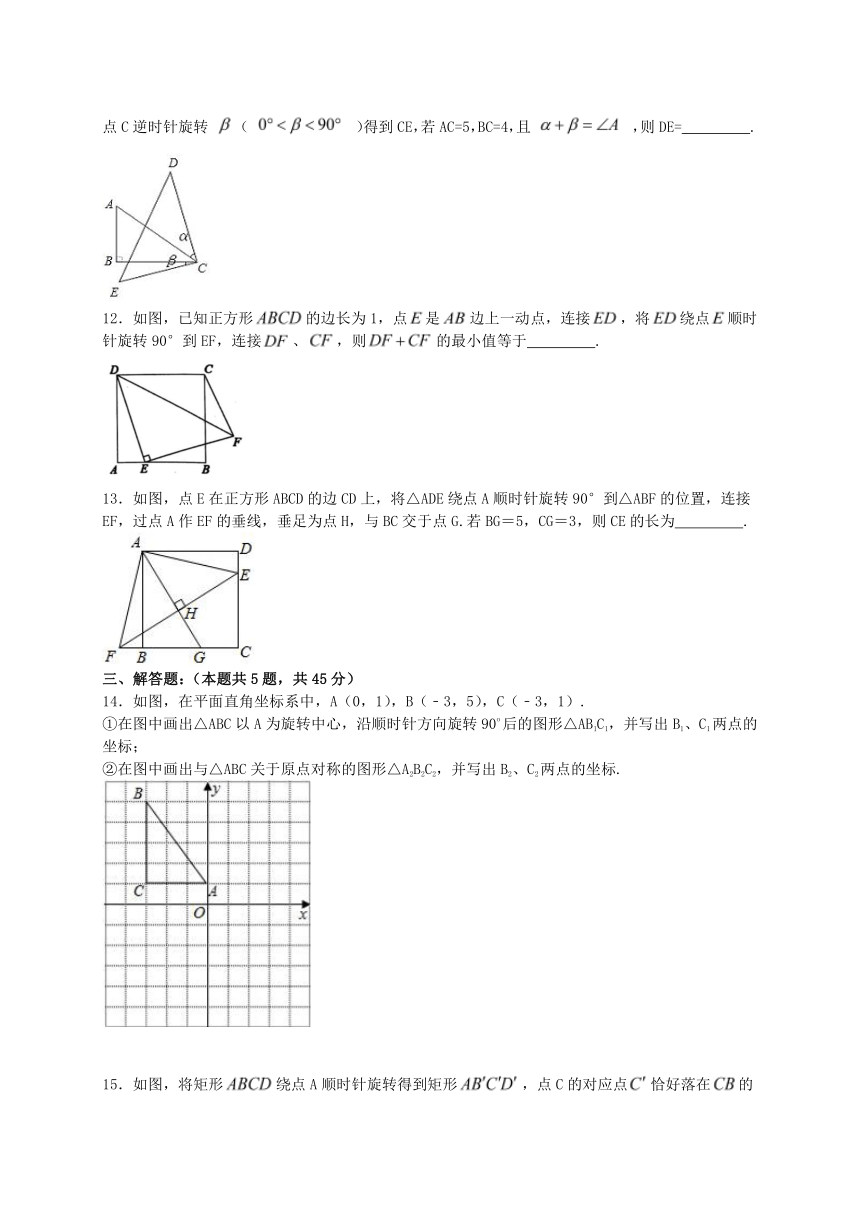
11.如图,将Rt△ABC的斜边AC绕点C顺时针旋转 ( )得到CD,直角边BC绕点C逆时针旋转 ( )得到CE,若AC=5,BC=4,且 ,则DE= .
12.如图,已知正方形的边长为1,点是边上一动点,连接,将绕点顺时针旋转90°到EF,连接、,则的最小值等于 .
13.如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若BG=5,CG=3,则CE的长为 .
三、解答题:(本题共5题,共45分)
14.如图,在平面直角坐标系中,A(0,1),B(﹣3,5),C(﹣3,1).
①在图中画出△ABC以A为旋转中心,沿顺时针方向旋转90o后的图形△AB1C1,并写出B1、C1两点的坐标;
②在图中画出与△ABC关于原点对称的图形△A2B2C2,并写出B2、C2两点的坐标.
15.如图,将矩形绕点A顺时针旋转得到矩形,点C的对应点恰好落在的延长线上,求证:.
16.如图,四边形ABCD是正方形.△ABE是等边三角形,M为对角线 BD(不含B,D点)上任意一点,将线段BM绕点B逆时针旋转60°得到BN,连接 EN,AM、CM.请判断线段 AM 和线段 EN 的数量关系,并说明理由.
17.如图,在Rt△ABC中,∠BAC=90°,∠ACB=30°,将△ABC绕点C逆时针旋转60°得到△CDE,点A、B的对应点分别是D、E,点F是边BC中点,连结AD、EF.
(1)求证:△ACD是等边三角形;
(2)判断AD与EF有怎样的数量关系,并说明理由.
18.如图,点O是平行四边形ABCD的对称中心,将直线DB绕点O顺时针方向旋转,交DC、AB于点E、F.
(1)证明:△DEO≌△BFO
(2)若DB=2,AD=1,AB=,当DB绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
参考答案:
1.A 2.A 3.B 4.C 5.B 6.D 7.D 8.C
9.(-2,1)
10.3
11.
12.
13.
14.解:如图所示:B1(4,4),C1(0,4),B2(3,﹣5),C2(3,﹣1).
15.证明:连接,,
∵四边形为矩形,
∴,
即.
由旋转,得.
∴.
16.解:AM=EN,理由为:
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,即∠EBN=∠ABN=60°,
∵线段BM绕点B逆时针旋转60°得到BN,
∴BM=BN,∠MBN=60°,即∠ABM+∠ABN=60°,
∴∠ABM=∠EBN,
在△ABM和△EBN中,
,
∴△ABM≌△EBN(SAS),
∴AM=EN.
17.(1)证明:∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴AC=CD,∠ACD=60°,
∴△ACD是等边三角形;
(2)解:AD=EF,理由如下:
∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴∠BCE=60°,BC=CE,
∵△ACD是等边三角形,
∴AD=AC,
∵点F是边BC中点,
∴BC=2CF,
∵∠BAC=90°,∠ACB=30°,
∴BC=2AB,∠ABC=60°=∠BCE,
∴AB=CF,
在△ABC和△DEC中,
,
∴△ABC≌△FCE(SAS),
∴EF=AC,
∴AD=EF.
18.(1)证明:在平行四边形ABCD中,CD∥AB,
∴∠CDO=∠ABO,∠DEO=∠BFO.
又∵点O是平行四边形的对称中心,
∴OD=OB.
∴△DEO≌△BFO.
(2)解:∵在△ABD中,DB=2,AD=1,AB=,
∴DB2+AD2=AB2.
∴△ABD是直角三角形,且∠ADB=90°
∵OD=OB=DB=1,
∴AD=OD=1.
∴△OAD是等腰直角三角形,
∴∠AOD=45°.
当直线DB绕点O顺时针旋转45°时,即∠DOE=45°,
∴∠AOE=90°
∵△DEO≌△BFO,
∴OE=OF
又∵点O是平行四边形的对称中心,∴OA=OC
∴四边形AECF是平行四边形
∴四边形AECF是菱形.
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列图案中既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,如果点P1(a,﹣3)与点P2(4,b)关于原点O对称,那么式子(a+b)2018的值为( )
A.1 B.﹣1 C.2018 D.﹣2018
3.如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
A.(1,1) B.(0,1) C.(﹣1,1) D.(2,0)
4.如图,一个小孩坐在秋千上,若秋千绕点O旋转了80°,小孩的位置也从A点运动到了B点,则∠OAB的度数为 ( )
A.70° B.60° C.50° D.40°
5.如图,把 绕点 顺时针旋转35°得到 , , 交 于点 ,若 ,则 的度数为( )
A.25° B.35° C.45° D.55°
6.如图,将矩形绕点逆时针旋转得到矩形,已知,则旋转角的度数为( )
A. B. C. D.
7.如图,在平面直角坐标系中,点A(﹣1,m)在直线y=2x+3上,连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=﹣x+b上,则b的值为( )
A.-2 B.1 C. D.2
8.已知,矩形中,,,点是线段上的一个动点,将线段绕点逆时针旋转得到,过作于点,连接,取的中点,连接,.点在运动过程中,下列结论:①;②当点和点互相重合时,;③;④.正确的有( )个.
A.1 B.2 C.3 D.4
二、填空题:(本题共5小题,每小题3分,共15分.)
9.点P(2,-1)关于原点成中心对称的点Q的坐标是 .
10.如图,中,,,.将绕点A逆时针旋转60°,得到,连接,则 .
11.如图,将Rt△ABC的斜边AC绕点C顺时针旋转 ( )得到CD,直角边BC绕点C逆时针旋转 ( )得到CE,若AC=5,BC=4,且 ,则DE= .
12.如图,已知正方形的边长为1,点是边上一动点,连接,将绕点顺时针旋转90°到EF,连接、,则的最小值等于 .
13.如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若BG=5,CG=3,则CE的长为 .
三、解答题:(本题共5题,共45分)
14.如图,在平面直角坐标系中,A(0,1),B(﹣3,5),C(﹣3,1).
①在图中画出△ABC以A为旋转中心,沿顺时针方向旋转90o后的图形△AB1C1,并写出B1、C1两点的坐标;
②在图中画出与△ABC关于原点对称的图形△A2B2C2,并写出B2、C2两点的坐标.
15.如图,将矩形绕点A顺时针旋转得到矩形,点C的对应点恰好落在的延长线上,求证:.
16.如图,四边形ABCD是正方形.△ABE是等边三角形,M为对角线 BD(不含B,D点)上任意一点,将线段BM绕点B逆时针旋转60°得到BN,连接 EN,AM、CM.请判断线段 AM 和线段 EN 的数量关系,并说明理由.
17.如图,在Rt△ABC中,∠BAC=90°,∠ACB=30°,将△ABC绕点C逆时针旋转60°得到△CDE,点A、B的对应点分别是D、E,点F是边BC中点,连结AD、EF.
(1)求证:△ACD是等边三角形;
(2)判断AD与EF有怎样的数量关系,并说明理由.
18.如图,点O是平行四边形ABCD的对称中心,将直线DB绕点O顺时针方向旋转,交DC、AB于点E、F.
(1)证明:△DEO≌△BFO
(2)若DB=2,AD=1,AB=,当DB绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
参考答案:
1.A 2.A 3.B 4.C 5.B 6.D 7.D 8.C
9.(-2,1)
10.3
11.
12.
13.
14.解:如图所示:B1(4,4),C1(0,4),B2(3,﹣5),C2(3,﹣1).
15.证明:连接,,
∵四边形为矩形,
∴,
即.
由旋转,得.
∴.
16.解:AM=EN,理由为:
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,即∠EBN=∠ABN=60°,
∵线段BM绕点B逆时针旋转60°得到BN,
∴BM=BN,∠MBN=60°,即∠ABM+∠ABN=60°,
∴∠ABM=∠EBN,
在△ABM和△EBN中,
,
∴△ABM≌△EBN(SAS),
∴AM=EN.
17.(1)证明:∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴AC=CD,∠ACD=60°,
∴△ACD是等边三角形;
(2)解:AD=EF,理由如下:
∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴∠BCE=60°,BC=CE,
∵△ACD是等边三角形,
∴AD=AC,
∵点F是边BC中点,
∴BC=2CF,
∵∠BAC=90°,∠ACB=30°,
∴BC=2AB,∠ABC=60°=∠BCE,
∴AB=CF,
在△ABC和△DEC中,
,
∴△ABC≌△FCE(SAS),
∴EF=AC,
∴AD=EF.
18.(1)证明:在平行四边形ABCD中,CD∥AB,
∴∠CDO=∠ABO,∠DEO=∠BFO.
又∵点O是平行四边形的对称中心,
∴OD=OB.
∴△DEO≌△BFO.
(2)解:∵在△ABD中,DB=2,AD=1,AB=,
∴DB2+AD2=AB2.
∴△ABD是直角三角形,且∠ADB=90°
∵OD=OB=DB=1,
∴AD=OD=1.
∴△OAD是等腰直角三角形,
∴∠AOD=45°.
当直线DB绕点O顺时针旋转45°时,即∠DOE=45°,
∴∠AOE=90°
∵△DEO≌△BFO,
∴OE=OF
又∵点O是平行四边形的对称中心,∴OA=OC
∴四边形AECF是平行四边形
∴四边形AECF是菱形.
同课章节目录
