第二十二章二次函数 单元练习(含答案) 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十二章二次函数 单元练习(含答案) 2023—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 421.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 21:00:17 | ||
图片预览


文档简介
第二十二章二次函数 单元练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.抛物线 (m是常数)的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知函数y=﹣x2+(m﹣1)x+m(m为常数),该函数图象与x轴公共点个数是( )
A.0 B.1 C.2 D.1或2
3.在西宁市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间满足函数解析式yx2x ,由此可知该生此次实心球训练的成绩为( )
A.6米 B.8米 C.10米 D.12米
4.如图,不考虑空气阻力,以一定的速度将小球沿斜上方击出时,小球在各自击出后2秒到达相同的最大飞行高度,若整个过程中(不考虑小球落地后再弹起),则t的取值范围是( )
A.0<t<2 B.2≤t<4 C.1≤t<3 D.3≤t<5
5.抛物线的图象经过点,则大小关系是( )
A. B.
C. D.
6. 如图,抛物线与直线交于,两点,则不等式的解集为( )
A. B. C. D.或
7.如图1,在矩形中,对角线与相交于点、动点从点出发,在线段上匀速运动,到达点时停止设点运动的路程为,线段的长为,如果与的函数图象如图所示,则矩形的面积是( )
A.60 B.48 C.24 D.12
8. 如图,二次函数的图象关于直线对称,与轴交于,两点,若,则下列四个结论:,,,,正确结论的个数为( )
A.个 B.个 C.个 D.个
二、填空题:(本题共5小题,每小题3分,共15分.)
9.抛物线与轴有 个交点.
10.直线y=2被抛物线y=x2﹣3x+2截得的线段长为 .
11.某超市一月份的营业额是200万元,一月、二月、三月的营业额共万元,如果平均每月增长率为,那么营业额关于月平均增长率的函数表达式为 .
12.将抛物线先向左平移2个单位长度,再向上平移个单位长度.若得到的抛物线经过点,则的值是 .
13.已知抛物线经过点,另有一点,在抛物线的对称轴上有一点,要使的值最大,则点的坐标是 .
三、解答题:(本题共5题,共45分)
14.已知 是 关于 的二次函数,且函数的图象经过点 ,试确定 的值.
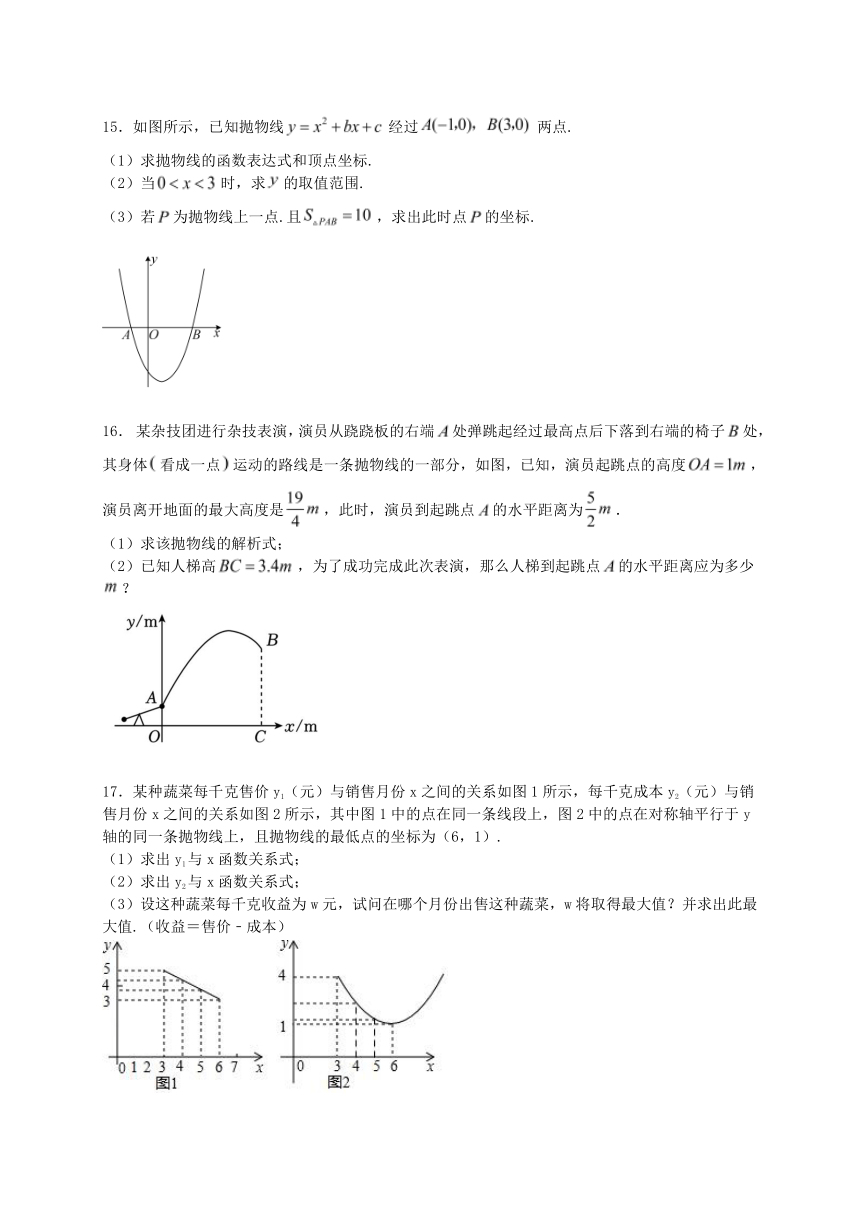
15.如图所示,已知抛物线经过两点.
(1)求拋物线的函数表达式和顶点坐标.
(2)当时,求的取值范围.
(3)若为抛物线上一点.且,求出此时点的坐标.
16. 某杂技团进行杂技表演,演员从跷跷板的右端处弹跳起经过最高点后下落到右端的椅子处,其身体看成一点运动的路线是一条抛物线的一部分,如图,已知,演员起跳点的高度,演员离开地面的最大高度是,此时,演员到起跳点的水平距离为.
(1)求该抛物线的解析式;
(2)已知人梯高,为了成功完成此次表演,那么人梯到起跳点的水平距离应为多少?
17.某种蔬菜每千克售价y1(元)与销售月份x之间的关系如图1所示,每千克成本y2(元)与销售月份x之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在对称轴平行于y轴的同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出y1与x函数关系式;
(2)求出y2与x函数关系式;
(3)设这种蔬菜每千克收益为w元,试问在哪个月份出售这种蔬菜,w将取得最大值?并求出此最大值.(收益=售价﹣成本)
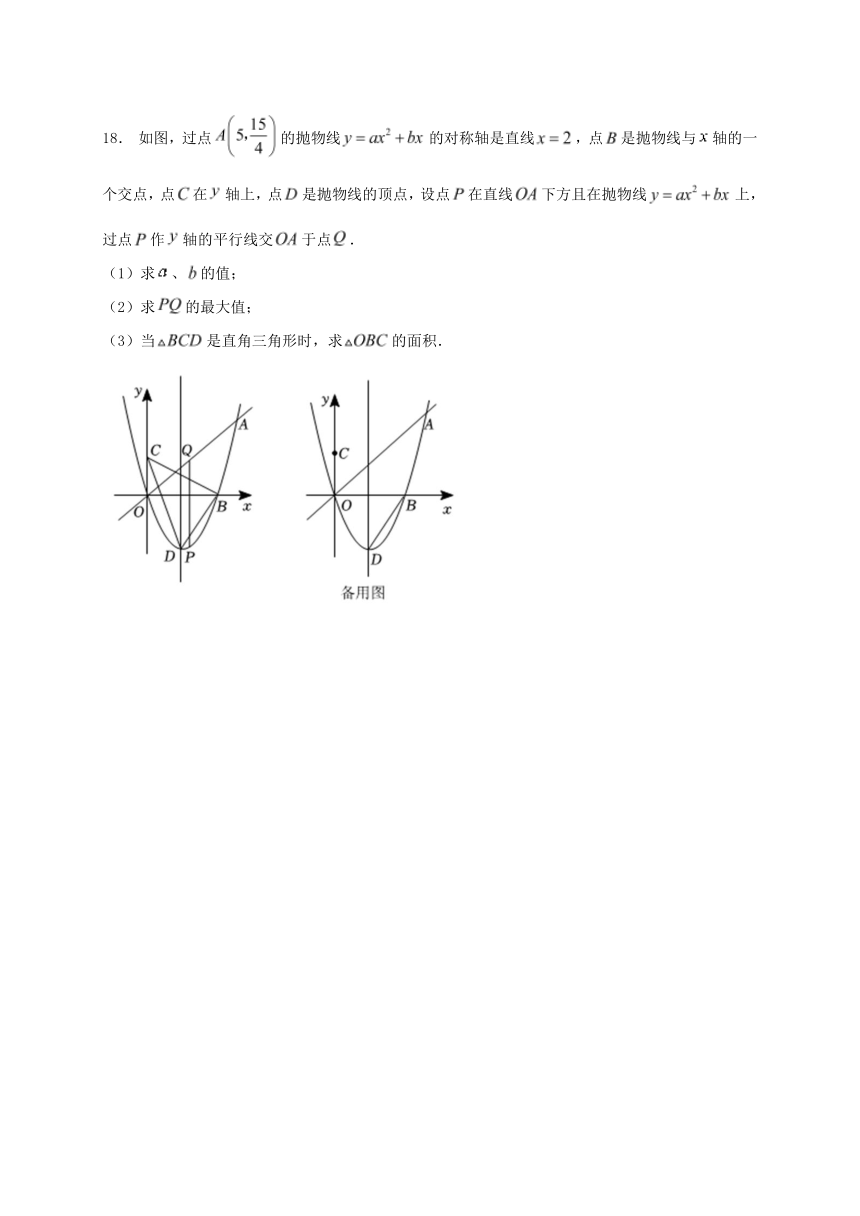
18. 如图,过点的抛物线的对称轴是直线,点是抛物线与轴的一个交点,点在轴上,点是抛物线的顶点,设点在直线下方且在抛物线上,过点作轴的平行线交于点.
(1)求、的值;
(2)求的最大值;
(3)当是直角三角形时,求的面积.
参考答案:
1.A 2.D 3.C 4.B 5.C 6.C 7.B 8.C
9.2
10.3
11.
12.4
13.
14.解: 二次函数 的图象经过点 ,
,
整理得: ,
解得: , ,
,
解得: ,
.
15.(1)解:把点的坐标分别代人,
得
解得,
抛物线的函数表达式为.
,
拋物线的顶点坐标为;
(2)解:∵B(3,0),顶点坐标为(1,-4),
∴由图象可得当0<x<3时,-4≤y<0;
(3)解:点,
.
设点,则,
(负值已舍).
令,解得,
点的坐标为或
16.(1)解:根据题意可知,抛物线的顶点坐标为
设抛物线的解析式为
把 代入得:
解得:
抛物线的解析式为
(2)解:当 时,
解得: 不符合题意,舍去,
答:人梯到起跳点 的水平距离应为 .
17.(1)解:设y1=kx+b,
∵直线经过(3,5)、(6,3),
,
解得: ,
∴y1=﹣ x+7(3≤x≤6,且x为整数)
(2)解:设y2=a(x﹣6)2+1,
把(3,4)代入得:4=a(3﹣6)2+1,
解得a= ,
∴y2= (x﹣6)2+1
(3)解:由题意得:w=y1﹣y2=﹣ x+7﹣[ (x﹣6)2+1],
=﹣ (x﹣5)2+ ,
当x=5时,w最大值= .
故5月出售这种蔬菜,每千克收益最大.
18.(1)解:过点的抛物线的对称轴是直线,
,解得,
故.
(2)解:设直线过点,可得直线.
由可得抛物线,
设,则,
,
当时,最大,最大值为.
(3)解:设点的坐标是由可得抛物线,
抛物线的顶点的坐标是,点的坐标是.
则,,,
当时,有.
,解得,
.
当时,有.
,解得,
.
当时,有.
,此方程无解.
综上所述,当为直角三角形时,的面积是或
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.抛物线 (m是常数)的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知函数y=﹣x2+(m﹣1)x+m(m为常数),该函数图象与x轴公共点个数是( )
A.0 B.1 C.2 D.1或2
3.在西宁市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间满足函数解析式yx2x ,由此可知该生此次实心球训练的成绩为( )
A.6米 B.8米 C.10米 D.12米
4.如图,不考虑空气阻力,以一定的速度将小球沿斜上方击出时,小球在各自击出后2秒到达相同的最大飞行高度,若整个过程中(不考虑小球落地后再弹起),则t的取值范围是( )
A.0<t<2 B.2≤t<4 C.1≤t<3 D.3≤t<5
5.抛物线的图象经过点,则大小关系是( )
A. B.
C. D.
6. 如图,抛物线与直线交于,两点,则不等式的解集为( )
A. B. C. D.或
7.如图1,在矩形中,对角线与相交于点、动点从点出发,在线段上匀速运动,到达点时停止设点运动的路程为,线段的长为,如果与的函数图象如图所示,则矩形的面积是( )
A.60 B.48 C.24 D.12
8. 如图,二次函数的图象关于直线对称,与轴交于,两点,若,则下列四个结论:,,,,正确结论的个数为( )
A.个 B.个 C.个 D.个
二、填空题:(本题共5小题,每小题3分,共15分.)
9.抛物线与轴有 个交点.
10.直线y=2被抛物线y=x2﹣3x+2截得的线段长为 .
11.某超市一月份的营业额是200万元,一月、二月、三月的营业额共万元,如果平均每月增长率为,那么营业额关于月平均增长率的函数表达式为 .
12.将抛物线先向左平移2个单位长度,再向上平移个单位长度.若得到的抛物线经过点,则的值是 .
13.已知抛物线经过点,另有一点,在抛物线的对称轴上有一点,要使的值最大,则点的坐标是 .
三、解答题:(本题共5题,共45分)
14.已知 是 关于 的二次函数,且函数的图象经过点 ,试确定 的值.
15.如图所示,已知抛物线经过两点.
(1)求拋物线的函数表达式和顶点坐标.
(2)当时,求的取值范围.
(3)若为抛物线上一点.且,求出此时点的坐标.
16. 某杂技团进行杂技表演,演员从跷跷板的右端处弹跳起经过最高点后下落到右端的椅子处,其身体看成一点运动的路线是一条抛物线的一部分,如图,已知,演员起跳点的高度,演员离开地面的最大高度是,此时,演员到起跳点的水平距离为.
(1)求该抛物线的解析式;
(2)已知人梯高,为了成功完成此次表演,那么人梯到起跳点的水平距离应为多少?
17.某种蔬菜每千克售价y1(元)与销售月份x之间的关系如图1所示,每千克成本y2(元)与销售月份x之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在对称轴平行于y轴的同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出y1与x函数关系式;
(2)求出y2与x函数关系式;
(3)设这种蔬菜每千克收益为w元,试问在哪个月份出售这种蔬菜,w将取得最大值?并求出此最大值.(收益=售价﹣成本)
18. 如图,过点的抛物线的对称轴是直线,点是抛物线与轴的一个交点,点在轴上,点是抛物线的顶点,设点在直线下方且在抛物线上,过点作轴的平行线交于点.
(1)求、的值;
(2)求的最大值;
(3)当是直角三角形时,求的面积.
参考答案:
1.A 2.D 3.C 4.B 5.C 6.C 7.B 8.C
9.2
10.3
11.
12.4
13.
14.解: 二次函数 的图象经过点 ,
,
整理得: ,
解得: , ,
,
解得: ,
.
15.(1)解:把点的坐标分别代人,
得
解得,
抛物线的函数表达式为.
,
拋物线的顶点坐标为;
(2)解:∵B(3,0),顶点坐标为(1,-4),
∴由图象可得当0<x<3时,-4≤y<0;
(3)解:点,
.
设点,则,
(负值已舍).
令,解得,
点的坐标为或
16.(1)解:根据题意可知,抛物线的顶点坐标为
设抛物线的解析式为
把 代入得:
解得:
抛物线的解析式为
(2)解:当 时,
解得: 不符合题意,舍去,
答:人梯到起跳点 的水平距离应为 .
17.(1)解:设y1=kx+b,
∵直线经过(3,5)、(6,3),
,
解得: ,
∴y1=﹣ x+7(3≤x≤6,且x为整数)
(2)解:设y2=a(x﹣6)2+1,
把(3,4)代入得:4=a(3﹣6)2+1,
解得a= ,
∴y2= (x﹣6)2+1
(3)解:由题意得:w=y1﹣y2=﹣ x+7﹣[ (x﹣6)2+1],
=﹣ (x﹣5)2+ ,
当x=5时,w最大值= .
故5月出售这种蔬菜,每千克收益最大.
18.(1)解:过点的抛物线的对称轴是直线,
,解得,
故.
(2)解:设直线过点,可得直线.
由可得抛物线,
设,则,
,
当时,最大,最大值为.
(3)解:设点的坐标是由可得抛物线,
抛物线的顶点的坐标是,点的坐标是.
则,,,
当时,有.
,解得,
.
当时,有.
,解得,
.
当时,有.
,此方程无解.
综上所述,当为直角三角形时,的面积是或
同课章节目录
