第二十二章《二次函数》章末复习题(含答案)2023-2024学年九年级上册数学人教版
文档属性
| 名称 | 第二十二章《二次函数》章末复习题(含答案)2023-2024学年九年级上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 248.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 21:00:41 | ||
图片预览


文档简介
第二十二章《二次函数》章末复习题
2023-2024学年九年级上册数学人教版
一、单选题(共10小题,满分40分)
1.下列函数中,表示y是x的二次函数的是( )
A. B. C. D.
2.已知二次函数的图象与轴的一个交点为(-1,0),对称轴是直线,则图象与轴的另一个交点是( )
A.(2,0) B.(-3,0) C.(-2,0) D.(3,0)
3.已知抛物线交x轴于点,.,是抛物线上两个点.若,则下列结论一定正确的是( )
A. B. C. D.
4.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度米,水流喷射的最远水平距离是( )
A.16米 B.18米 C.20米 D.24米
5.将抛物线向左平移2个单位,再向下平移1个单位,则所得的抛物线的解析式为( )
A. B.
C. D.
6.二次函数y=﹣2(x+2)2﹣4,下列说法正确的是( )
A.开口向上 B.对称轴为直线x=2
C.顶点坐标为(-2,4) D.当x<﹣2时,y随x的增大而增大
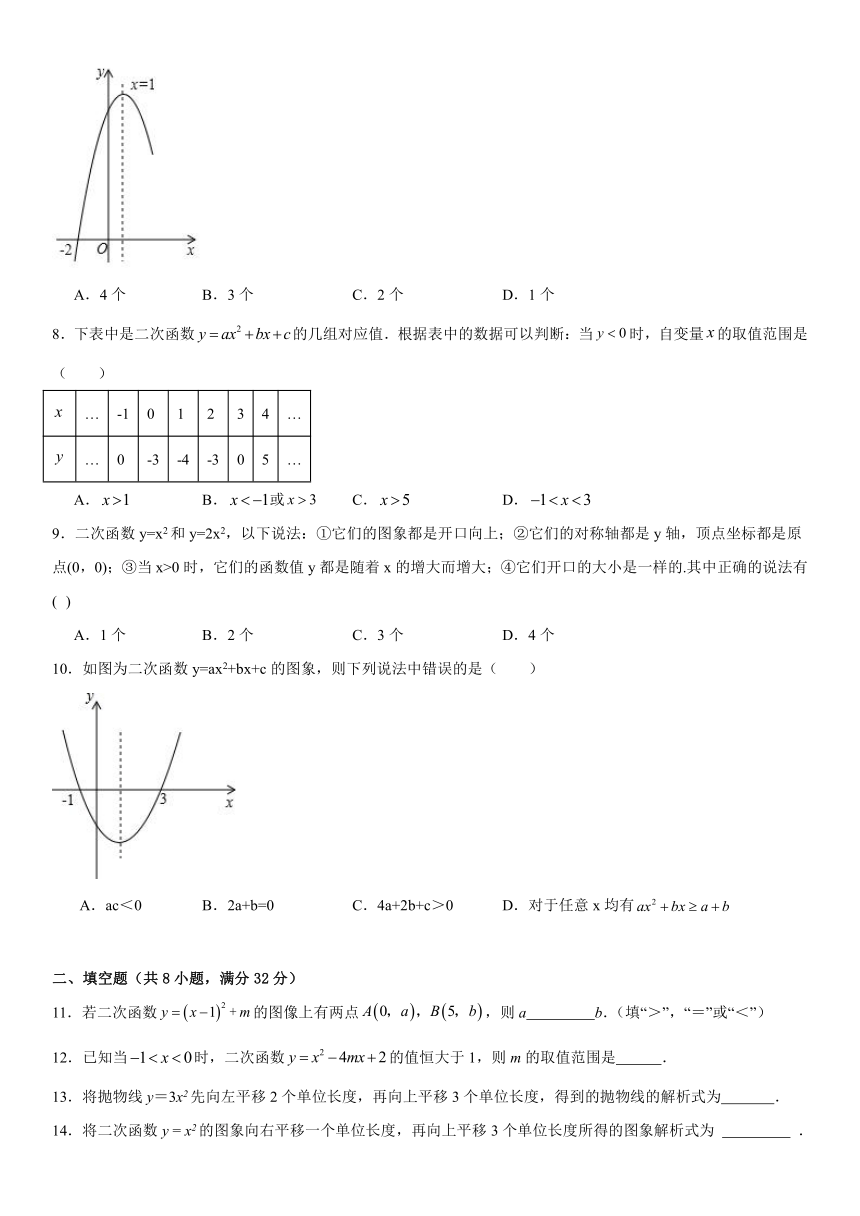
7.抛物线y=ax2+bx+c经过点(-2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:①b=2a;②4a+2b+c>0;③若n>m>0,则x=1+m时的函数值小于x=1-n时的函数值;④点一定在此抛物线上.其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
8.下表中是二次函数的几组对应值.根据表中的数据可以判断:当时,自变量的取值范围是( )
… -1 0 1 2 3 4 …
… 0 -3 -4 -3 0 5 …
A. B.或 C. D.
9.二次函数y=x2和y=2x2,以下说法:①它们的图象都是开口向上;②它们的对称轴都是y轴,顶点坐标都是原点(0,0);③当x>0时,它们的函数值y都是随着x的增大而增大;④它们开口的大小是一样的.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
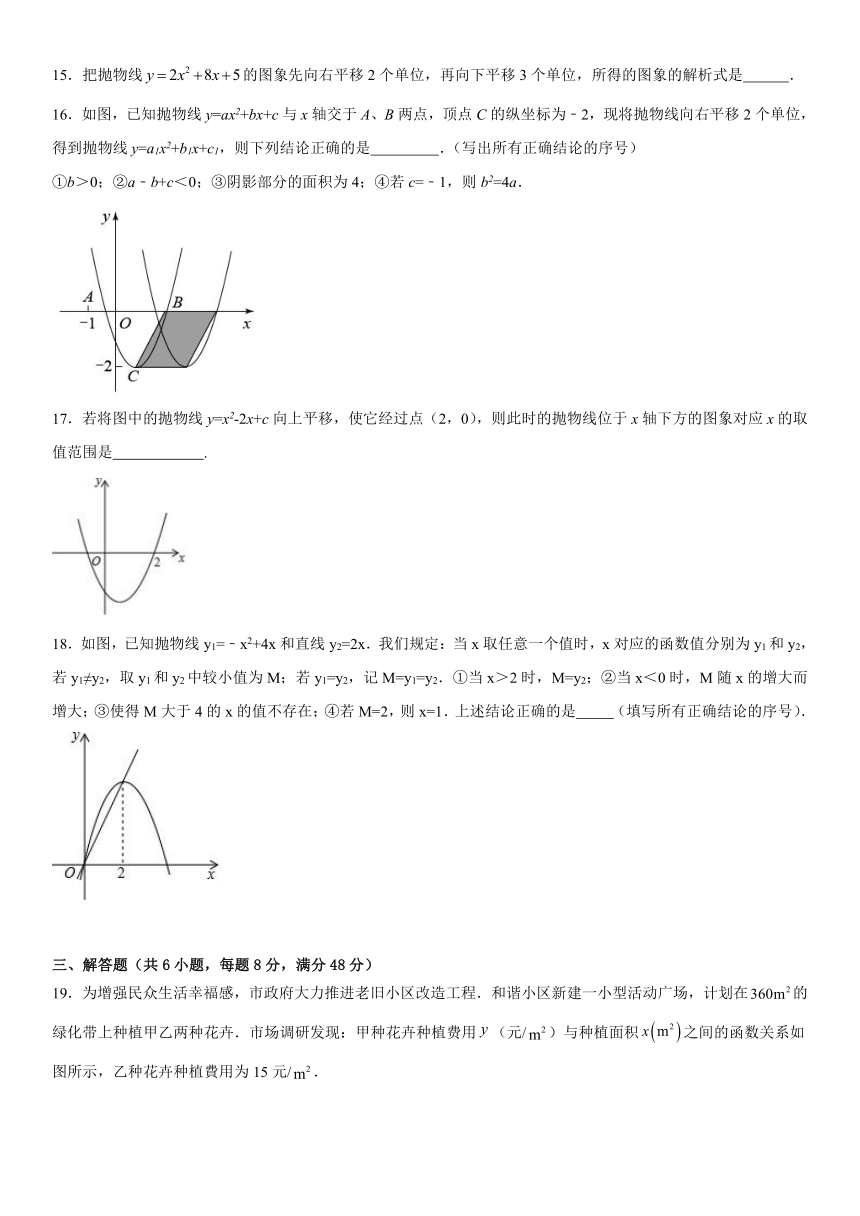
10.如图为二次函数y=ax2+bx+c的图象,则下列说法中错误的是( )
A.ac<0 B.2a+b=0 C.4a+2b+c>0 D.对于任意x均有
二、填空题(共8小题,满分32分)
11.若二次函数的图像上有两点,则a b.(填“>”,“=”或“<”)
12.已知当时,二次函数的值恒大于1,则m的取值范围是 .
13.将抛物线y=3x2先向左平移2个单位长度,再向上平移3个单位长度,得到的抛物线的解析式为 .
14.将二次函数y = x2的图象向右平移一个单位长度,再向上平移3个单位长度所得的图象解析式为 .
15.把抛物线的图象先向右平移2个单位,再向下平移3个单位,所得的图象的解析式是 .
16.如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是 .(写出所有正确结论的序号)
①b>0;②a﹣b+c<0;③阴影部分的面积为4;④若c=﹣1,则b2=4a.
17.若将图中的抛物线y=x2-2x+c向上平移,使它经过点(2,0),则此时的抛物线位于x轴下方的图象对应x的取值范围是 .
18.如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2,若y1≠y2,取y1和y2中较小值为M;若y1=y2,记M=y1=y2.①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是 (填写所有正确结论的序号).
三、解答题(共6小题,每题8分,满分48分)
19.为增强民众生活幸福感,市政府大力推进老旧小区改造工程.和谐小区新建一小型活动广场,计划在的绿化带上种植甲乙两种花卉.市场调研发现:甲种花卉种植费用(元/)与种植面积之间的函数关系如图所示,乙种花卉种植費用为15元/.
(1)当时,求与的函数关系式;
(2)当甲种花卉种植面积不少于,且乙种花卉种植面积不低于甲种花卉种植面积的3倍时.如何分配甲乙两种花卉的种植面积才能使种植的总费用(元)最少?
20.如图,抛物线y=x2+bx+c经过点(﹣2,5)和(2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.
(1)求该抛物线的表达式;
(2)求出点A,B,C的坐标;
(3)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P,D,E为顶点的三角形与△BOC全等,求满足条件的点P,点E的坐标.
21.如图是抛物线型拱桥,当拱顶离水面2米时,水面宽4米.
(1)以抛物线的顶点为原点,抛物线的对称轴为y轴建立直角坐标系,请在图中画出坐标系,并求出抛物线的解析式;
(2)当水面下降1米时,水面宽度增加了多少米?
22.某网站店主购进A、B两种型号的装饰链,其中A型装饰链的进货单价比B型装饰链的进货单价多20元,花500元购进A型装饰链的数量与花400元购进B型装饰链的数量相等.销售中发现A型装饰链的每月销售量y1(个)与销售单价x(元)之间满足的函数关系式为y1=-x+200;B型装饰链的每月销售量y2(个)与销售单价x(元)满足的关系式为y2=-x+140
(1)求A、B两种型号装饰链的进货单价;
(2)已知每个A型装饰链的销售单价比B型装饰链的销售单价高20元.求A、B两种型号装饰链的销售单价各为多少元时,每月销售这两种装饰链的总利润最大,最大总利润是多少?
23.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
24.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(﹣1,0),B(0,3),O(0,0),将此三角板绕原点O顺时针旋转90°,得到△A′B′O.
⑴如图,一抛物线经过点A,B,B′,求该抛物线解析式;
⑵设点P是在第一象限内抛物线上一动点,求使四边形PBAB′的面积达到最大时点P的坐标及面积的最大值.
参考答案:
1.B
2.D
3.D
4.C
5.B
6.D
7.C
8.D
9.C
10.C
11.<
12.
13.
14.y=(x-1)2+3
15.
16.③④/④③
17.0<x<2
18.②③
19.(1)
(2)甲种花卉种植面积为,乙种花卉种植面积为,才能使种植的总费用w(元)最少,最少为5625元
20.(1);(2);(3)的坐标为:的坐标为:
21.(1)
(2)当水面下降1米时,水面宽度增加了米
22.(1)A:100元;B:80元
(2)A:140元,B:120元时,W最大=3200
23.(1)抛物线解析式为y=﹣x2+2x+3;直线AC的解析式为y=3x+3;(2)点M的坐标为(0,3);
(3)符合条件的点P的坐标为(,)或(,﹣),
24.(1)y=-x2+2x+3;(2)P(,);S最大=.
2023-2024学年九年级上册数学人教版
一、单选题(共10小题,满分40分)
1.下列函数中,表示y是x的二次函数的是( )
A. B. C. D.
2.已知二次函数的图象与轴的一个交点为(-1,0),对称轴是直线,则图象与轴的另一个交点是( )
A.(2,0) B.(-3,0) C.(-2,0) D.(3,0)
3.已知抛物线交x轴于点,.,是抛物线上两个点.若,则下列结论一定正确的是( )
A. B. C. D.
4.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度米,水流喷射的最远水平距离是( )
A.16米 B.18米 C.20米 D.24米
5.将抛物线向左平移2个单位,再向下平移1个单位,则所得的抛物线的解析式为( )
A. B.
C. D.
6.二次函数y=﹣2(x+2)2﹣4,下列说法正确的是( )
A.开口向上 B.对称轴为直线x=2
C.顶点坐标为(-2,4) D.当x<﹣2时,y随x的增大而增大
7.抛物线y=ax2+bx+c经过点(-2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:①b=2a;②4a+2b+c>0;③若n>m>0,则x=1+m时的函数值小于x=1-n时的函数值;④点一定在此抛物线上.其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
8.下表中是二次函数的几组对应值.根据表中的数据可以判断:当时,自变量的取值范围是( )
… -1 0 1 2 3 4 …
… 0 -3 -4 -3 0 5 …
A. B.或 C. D.
9.二次函数y=x2和y=2x2,以下说法:①它们的图象都是开口向上;②它们的对称轴都是y轴,顶点坐标都是原点(0,0);③当x>0时,它们的函数值y都是随着x的增大而增大;④它们开口的大小是一样的.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
10.如图为二次函数y=ax2+bx+c的图象,则下列说法中错误的是( )
A.ac<0 B.2a+b=0 C.4a+2b+c>0 D.对于任意x均有
二、填空题(共8小题,满分32分)
11.若二次函数的图像上有两点,则a b.(填“>”,“=”或“<”)
12.已知当时,二次函数的值恒大于1,则m的取值范围是 .
13.将抛物线y=3x2先向左平移2个单位长度,再向上平移3个单位长度,得到的抛物线的解析式为 .
14.将二次函数y = x2的图象向右平移一个单位长度,再向上平移3个单位长度所得的图象解析式为 .
15.把抛物线的图象先向右平移2个单位,再向下平移3个单位,所得的图象的解析式是 .
16.如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是 .(写出所有正确结论的序号)
①b>0;②a﹣b+c<0;③阴影部分的面积为4;④若c=﹣1,则b2=4a.
17.若将图中的抛物线y=x2-2x+c向上平移,使它经过点(2,0),则此时的抛物线位于x轴下方的图象对应x的取值范围是 .
18.如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2,若y1≠y2,取y1和y2中较小值为M;若y1=y2,记M=y1=y2.①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是 (填写所有正确结论的序号).
三、解答题(共6小题,每题8分,满分48分)
19.为增强民众生活幸福感,市政府大力推进老旧小区改造工程.和谐小区新建一小型活动广场,计划在的绿化带上种植甲乙两种花卉.市场调研发现:甲种花卉种植费用(元/)与种植面积之间的函数关系如图所示,乙种花卉种植費用为15元/.
(1)当时,求与的函数关系式;
(2)当甲种花卉种植面积不少于,且乙种花卉种植面积不低于甲种花卉种植面积的3倍时.如何分配甲乙两种花卉的种植面积才能使种植的总费用(元)最少?
20.如图,抛物线y=x2+bx+c经过点(﹣2,5)和(2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.
(1)求该抛物线的表达式;
(2)求出点A,B,C的坐标;
(3)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P,D,E为顶点的三角形与△BOC全等,求满足条件的点P,点E的坐标.
21.如图是抛物线型拱桥,当拱顶离水面2米时,水面宽4米.
(1)以抛物线的顶点为原点,抛物线的对称轴为y轴建立直角坐标系,请在图中画出坐标系,并求出抛物线的解析式;
(2)当水面下降1米时,水面宽度增加了多少米?
22.某网站店主购进A、B两种型号的装饰链,其中A型装饰链的进货单价比B型装饰链的进货单价多20元,花500元购进A型装饰链的数量与花400元购进B型装饰链的数量相等.销售中发现A型装饰链的每月销售量y1(个)与销售单价x(元)之间满足的函数关系式为y1=-x+200;B型装饰链的每月销售量y2(个)与销售单价x(元)满足的关系式为y2=-x+140
(1)求A、B两种型号装饰链的进货单价;
(2)已知每个A型装饰链的销售单价比B型装饰链的销售单价高20元.求A、B两种型号装饰链的销售单价各为多少元时,每月销售这两种装饰链的总利润最大,最大总利润是多少?
23.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
24.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(﹣1,0),B(0,3),O(0,0),将此三角板绕原点O顺时针旋转90°,得到△A′B′O.
⑴如图,一抛物线经过点A,B,B′,求该抛物线解析式;
⑵设点P是在第一象限内抛物线上一动点,求使四边形PBAB′的面积达到最大时点P的坐标及面积的最大值.
参考答案:
1.B
2.D
3.D
4.C
5.B
6.D
7.C
8.D
9.C
10.C
11.<
12.
13.
14.y=(x-1)2+3
15.
16.③④/④③
17.0<x<2
18.②③
19.(1)
(2)甲种花卉种植面积为,乙种花卉种植面积为,才能使种植的总费用w(元)最少,最少为5625元
20.(1);(2);(3)的坐标为:的坐标为:
21.(1)
(2)当水面下降1米时,水面宽度增加了米
22.(1)A:100元;B:80元
(2)A:140元,B:120元时,W最大=3200
23.(1)抛物线解析式为y=﹣x2+2x+3;直线AC的解析式为y=3x+3;(2)点M的坐标为(0,3);
(3)符合条件的点P的坐标为(,)或(,﹣),
24.(1)y=-x2+2x+3;(2)P(,);S最大=.
同课章节目录
