2023-2024学年苏科版数学八年级上册 3.3勾股定理的简单应用学案(五大典型题型培优练习)(无答案)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册 3.3勾股定理的简单应用学案(五大典型题型培优练习)(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 326.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 21:12:26 | ||
图片预览


文档简介
3.3勾股定理的简单应用
(五大典型题型培优练习)
【学习目标】
掌握梯子滑落问题
掌握航海问题
掌握求旗杆高度问题
掌握是否超速问题
掌握最短路径问题
【典型例题】
类型一、梯子滑落问题
【例1】如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.如果梯子的顶端A下滑了4米,那么梯子底端C在水平方向滑动了( )米
A.7米 B.8米 C.9米 D.10米
举一反三:
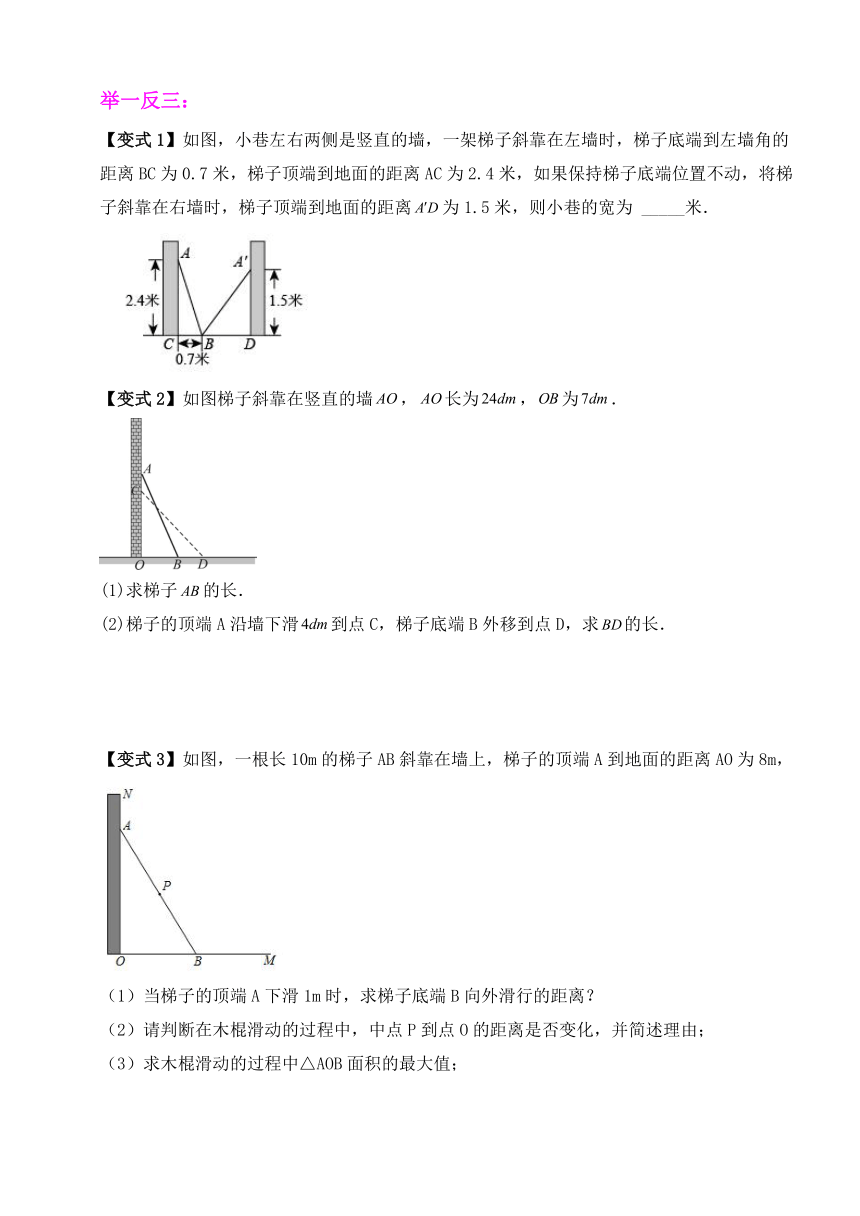
【变式1】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为1.5米,则小巷的宽为 _____米.
【变式2】如图梯子斜靠在竖直的墙,长为,为.
(1)求梯子的长.
(2)梯子的顶端A沿墙下滑到点C,梯子底端B外移到点D,求的长.
【变式3】如图,一根长10m的梯子AB斜靠在墙上,梯子的顶端A到地面的距离AO为8m,
(1)当梯子的顶端A下滑1m时,求梯子底端B向外滑行的距离?
(2)请判断在木棍滑动的过程中,中点P到点O的距离是否变化,并简述理由;
(3)求木棍滑动的过程中△AOB面积的最大值;
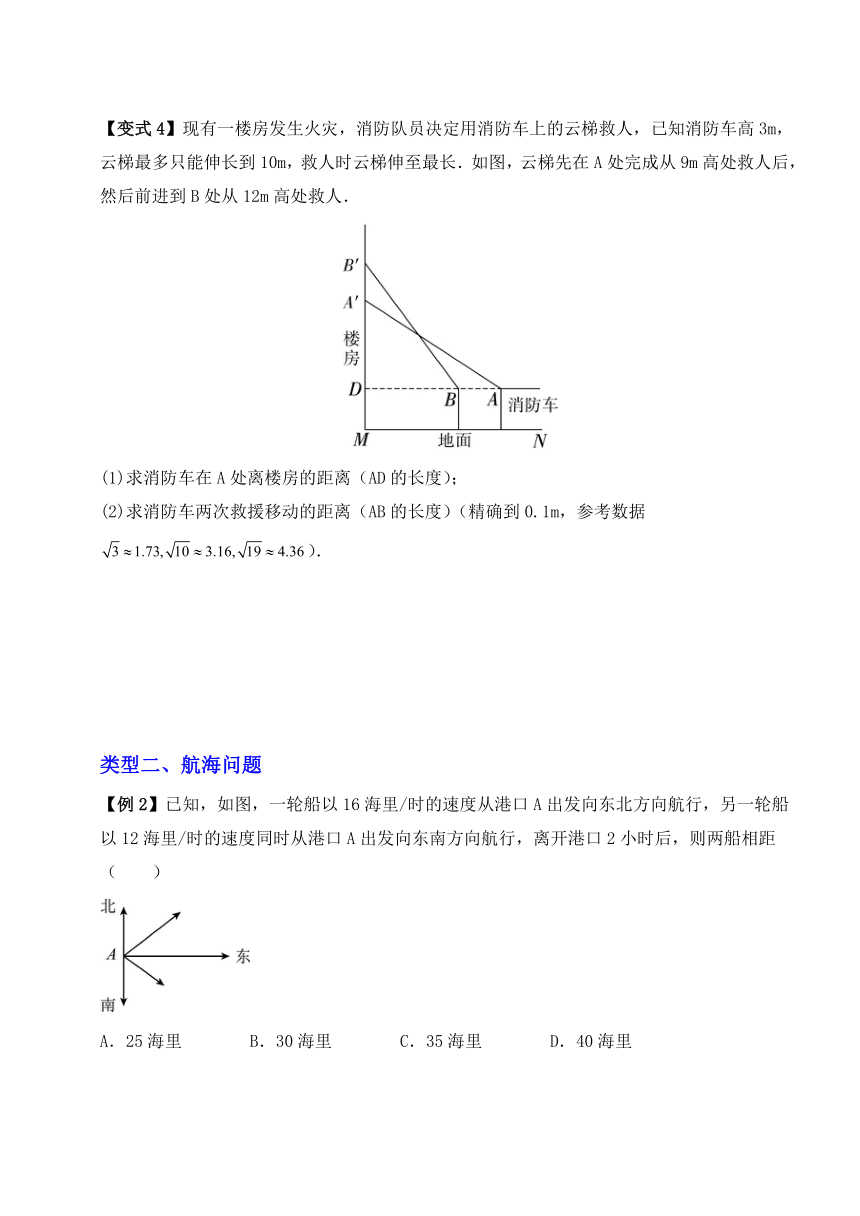
【变式4】现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,已知消防车高3m,云梯最多只能伸长到10m,救人时云梯伸至最长.如图,云梯先在A处完成从9m高处救人后,然后前进到B处从12m高处救人.
(1)求消防车在A处离楼房的距离(AD的长度);
(2)求消防车两次救援移动的距离(AB的长度)(精确到0.1m,参考数据).
类型二、航海问题
【例2】已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
A.25海里 B.30海里 C.35海里 D.40海里
举一反三:
【变式1】轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则B处与灯塔A的距离是__________海里.
【变式2】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD.
【变式3】甲、乙两船同时从港口A出发,甲船以30海里/时的速度沿北偏东35°方向航行,乙船沿南偏东55°向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,问乙船的速度是每小时多少海里?
【变式4】台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向由行驶向,已知点为一海港,且点与直线上的两点,的距离分别为,,又,以台风中心为圆心周围以内为受影响区域.
(1)求的度数.
(2)海港受台风影响吗?为什么?
(3)若台风的速度为千米/小时,当台风运动到点处时,海港刚好受到影响,当台风运动到点时,海港刚好不受影响,即,则台风影响该海港持续的时间有多长?
类型三、旗杆高度问题
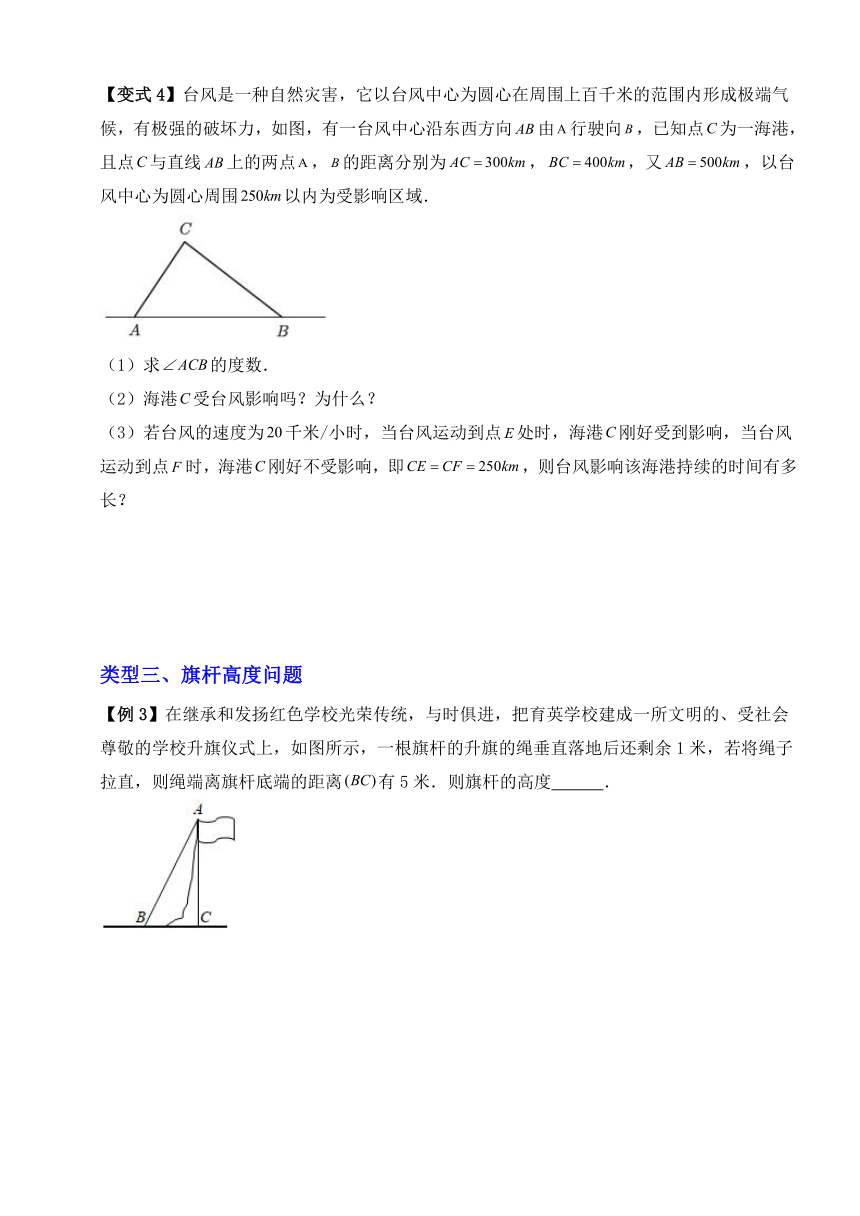
【例3】在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离有5米.则旗杆的高度 .
举一反三:
【变式1】小红同学测量学校旗杆的高度,她发现旗杆的绳子刚好垂到地面上,当她把绳子下端拉开,发现此时绳子的下端距离旗杆5m,距地面1m,则学校旗杆的高度是( )
A.8m B.10m C.12m D.13m
【变式2】小亮想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多2m,当他把绳子的下端拉开8m后,下端刚好接触到地面,则学校旗杆的高度为( )
A.m B.m C.m D.m
【变式3】如图所示,小刚想知道学校的旗杆有多高,他发现旗杆上的绳子垂到地面还多了0.8m,当他把绳子下端拉开4m后,发现下端刚好接触地面,小刚算了算就知道了旗杆的高度.你知道他是怎样算出来的吗?
【变式4】如图,同学们想测量旗杆的高度(米),他们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.小明和小亮同学应用勾股定理分别提出解决这个问题的方案如下:
小明:①测量出绳子垂直落地后还剩余米,如图;
②把绳子拉直,绳子末端在地面上离旗杆底部米,如图.
小亮:先在旗杆底端的绳子上打了一个结,然后举起绳结拉到如图点处().
(1)请你按小明的方案求出旗杆的高度h(米);
(2)已知小亮举起绳结离旗杆米远,此时绳结离地面多高?
类型四、是否超速问题
【例4】在某段公路的正上方有一摄像头A距离地面7米,一天李叔叔驾驶的汽车正沿公路笔直匀速驶来,当行驶到B点时第一次摄像,此时AB两点相距25米,1.5秒后第二次摄像汽车恰好行驶到A点正下方C点,已知该路段限速60km/h,请判断李叔叔是否超速,说明理由.
举一反三:
【变式1】交通安全一直是社会关注的热点问题,主要安全隐患是超速和超载.交警部门在近年来事故多发的危险路段设立了固定测速点.如图,先在笔直的公路l旁选取一点P,在公路l上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,测得一辆轿车从B处匀速行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由.(参考数据:1.41,1.73,1米/秒=3.6千米/时)
【变式2】某条道路限速,如图,一辆小汽车在这条道路上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方的C处,过了后,小汽车到达B处,此时测得小汽车与车速测检测仪间的距离为,这辆小汽车超速了吗?
【变式3】某条道路限速,如图,一辆小汽车在这条道路上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方的C处,过了,小汽车到达B处,此时测得小汽车与车速检测仪间的距离为.
(1)求的长;
(2)这辆小汽车超速了吗?
如图,A中学位于南北向公路l的一侧,门前有两条长度均为100米的小路通往公路l,与公路l交于B,C两点,且B,C相距120米.
【变式4】
(1)现在想修一条从公路l到A中学的新路(点D在l上),使得学生从公路l走到学校路程最短,应该如何修路(请在图中画出)?新路长度是多少?
(2)为了行车安全,在公路l上的点B和点E处设置了一组区间测速装置,其中点E在点B的北侧,且距A中学170米.一辆车经过区间用时5秒,若公路l限速为(约),请判断该车是否超速,并说明理由.
类型五、最短路径问题
【例5】如图,长方体的长为,宽为,高为,点到点的距离为,一只蚂蚁如果要沿着长方体的表面从点爬到点,需要爬行的最短距离是( )
A.4 B.5 C. D.
举一反三:
【变式1】如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
【变式2】如图是放在地面上的一个长方体盒子,其中,,,点在棱上,且,点是的中点,一只蚂蚁要沿着长方体盒子的表面从点爬行到点,它需要爬行的最短路程是多少?
【变式3】如图所示是一个三级台阶,它的每一级的长、宽、高分别等于5cm、3cm、1cm,A和B是这两个台阶的两个相对的端点,则一只蚂蚁从点A出发经过台阶爬到点B的最短路线有多长?
【变式4】如图①,长方体长AB为8 cm,宽BC为6 cm,高BF为4 cm.在该长体的表面上,蚂蚁怎样爬行路径最短?
(1)蚂蚁从点A爬行到点G,且经过棱EF上一点,画出其最短路径的平面图,并标出它的长.
(2)设该长方体上底面对角线EG、FH相交于点O(如图②),则OE=OF=OG=OH=5 cm.
①蚂蚁从点B爬行到点O的最短路径的长为 cm;
②当点P在BC边上,设BP长为a cm,求蚂蚁从点P爬行到点O的最短路的长(用含a的代数式表示).
(五大典型题型培优练习)
【学习目标】
掌握梯子滑落问题
掌握航海问题
掌握求旗杆高度问题
掌握是否超速问题
掌握最短路径问题
【典型例题】
类型一、梯子滑落问题
【例1】如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.如果梯子的顶端A下滑了4米,那么梯子底端C在水平方向滑动了( )米
A.7米 B.8米 C.9米 D.10米
举一反三:
【变式1】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为1.5米,则小巷的宽为 _____米.
【变式2】如图梯子斜靠在竖直的墙,长为,为.
(1)求梯子的长.
(2)梯子的顶端A沿墙下滑到点C,梯子底端B外移到点D,求的长.
【变式3】如图,一根长10m的梯子AB斜靠在墙上,梯子的顶端A到地面的距离AO为8m,
(1)当梯子的顶端A下滑1m时,求梯子底端B向外滑行的距离?
(2)请判断在木棍滑动的过程中,中点P到点O的距离是否变化,并简述理由;
(3)求木棍滑动的过程中△AOB面积的最大值;
【变式4】现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,已知消防车高3m,云梯最多只能伸长到10m,救人时云梯伸至最长.如图,云梯先在A处完成从9m高处救人后,然后前进到B处从12m高处救人.
(1)求消防车在A处离楼房的距离(AD的长度);
(2)求消防车两次救援移动的距离(AB的长度)(精确到0.1m,参考数据).
类型二、航海问题
【例2】已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
A.25海里 B.30海里 C.35海里 D.40海里
举一反三:
【变式1】轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则B处与灯塔A的距离是__________海里.
【变式2】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD.
【变式3】甲、乙两船同时从港口A出发,甲船以30海里/时的速度沿北偏东35°方向航行,乙船沿南偏东55°向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,问乙船的速度是每小时多少海里?
【变式4】台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向由行驶向,已知点为一海港,且点与直线上的两点,的距离分别为,,又,以台风中心为圆心周围以内为受影响区域.
(1)求的度数.
(2)海港受台风影响吗?为什么?
(3)若台风的速度为千米/小时,当台风运动到点处时,海港刚好受到影响,当台风运动到点时,海港刚好不受影响,即,则台风影响该海港持续的时间有多长?
类型三、旗杆高度问题
【例3】在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离有5米.则旗杆的高度 .
举一反三:
【变式1】小红同学测量学校旗杆的高度,她发现旗杆的绳子刚好垂到地面上,当她把绳子下端拉开,发现此时绳子的下端距离旗杆5m,距地面1m,则学校旗杆的高度是( )
A.8m B.10m C.12m D.13m
【变式2】小亮想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多2m,当他把绳子的下端拉开8m后,下端刚好接触到地面,则学校旗杆的高度为( )
A.m B.m C.m D.m
【变式3】如图所示,小刚想知道学校的旗杆有多高,他发现旗杆上的绳子垂到地面还多了0.8m,当他把绳子下端拉开4m后,发现下端刚好接触地面,小刚算了算就知道了旗杆的高度.你知道他是怎样算出来的吗?
【变式4】如图,同学们想测量旗杆的高度(米),他们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.小明和小亮同学应用勾股定理分别提出解决这个问题的方案如下:
小明:①测量出绳子垂直落地后还剩余米,如图;
②把绳子拉直,绳子末端在地面上离旗杆底部米,如图.
小亮:先在旗杆底端的绳子上打了一个结,然后举起绳结拉到如图点处().
(1)请你按小明的方案求出旗杆的高度h(米);
(2)已知小亮举起绳结离旗杆米远,此时绳结离地面多高?
类型四、是否超速问题
【例4】在某段公路的正上方有一摄像头A距离地面7米,一天李叔叔驾驶的汽车正沿公路笔直匀速驶来,当行驶到B点时第一次摄像,此时AB两点相距25米,1.5秒后第二次摄像汽车恰好行驶到A点正下方C点,已知该路段限速60km/h,请判断李叔叔是否超速,说明理由.
举一反三:
【变式1】交通安全一直是社会关注的热点问题,主要安全隐患是超速和超载.交警部门在近年来事故多发的危险路段设立了固定测速点.如图,先在笔直的公路l旁选取一点P,在公路l上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,测得一辆轿车从B处匀速行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由.(参考数据:1.41,1.73,1米/秒=3.6千米/时)
【变式2】某条道路限速,如图,一辆小汽车在这条道路上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方的C处,过了后,小汽车到达B处,此时测得小汽车与车速测检测仪间的距离为,这辆小汽车超速了吗?
【变式3】某条道路限速,如图,一辆小汽车在这条道路上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方的C处,过了,小汽车到达B处,此时测得小汽车与车速检测仪间的距离为.
(1)求的长;
(2)这辆小汽车超速了吗?
如图,A中学位于南北向公路l的一侧,门前有两条长度均为100米的小路通往公路l,与公路l交于B,C两点,且B,C相距120米.
【变式4】
(1)现在想修一条从公路l到A中学的新路(点D在l上),使得学生从公路l走到学校路程最短,应该如何修路(请在图中画出)?新路长度是多少?
(2)为了行车安全,在公路l上的点B和点E处设置了一组区间测速装置,其中点E在点B的北侧,且距A中学170米.一辆车经过区间用时5秒,若公路l限速为(约),请判断该车是否超速,并说明理由.
类型五、最短路径问题
【例5】如图,长方体的长为,宽为,高为,点到点的距离为,一只蚂蚁如果要沿着长方体的表面从点爬到点,需要爬行的最短距离是( )
A.4 B.5 C. D.
举一反三:
【变式1】如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
【变式2】如图是放在地面上的一个长方体盒子,其中,,,点在棱上,且,点是的中点,一只蚂蚁要沿着长方体盒子的表面从点爬行到点,它需要爬行的最短路程是多少?
【变式3】如图所示是一个三级台阶,它的每一级的长、宽、高分别等于5cm、3cm、1cm,A和B是这两个台阶的两个相对的端点,则一只蚂蚁从点A出发经过台阶爬到点B的最短路线有多长?
【变式4】如图①,长方体长AB为8 cm,宽BC为6 cm,高BF为4 cm.在该长体的表面上,蚂蚁怎样爬行路径最短?
(1)蚂蚁从点A爬行到点G,且经过棱EF上一点,画出其最短路径的平面图,并标出它的长.
(2)设该长方体上底面对角线EG、FH相交于点O(如图②),则OE=OF=OG=OH=5 cm.
①蚂蚁从点B爬行到点O的最短路径的长为 cm;
②当点P在BC边上,设BP长为a cm,求蚂蚁从点P爬行到点O的最短路的长(用含a的代数式表示).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
