人教版八年级上册 11.2.2三角形的外角课件 16张PPT
文档属性
| 名称 | 人教版八年级上册 11.2.2三角形的外角课件 16张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 678.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 21:21:20 | ||
图片预览






文档简介
(共16张PPT)
§11.2.2 三角形的外角
回顾旧知
1.三角形内角和等于_______________.
180 °
2.如图,在△ABC中, ∠A=70°, ∠B=60°,
则∠ACB= .
50 °
阅读书本P14-15 3分钟
合作探究---三角形的外角的概念
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACD是△ABC的一个外角
C
B
A
D
例1:判断下列图中的∠1是否为△ABC的外角.
问题1:如图,试着画出△ABC的所有外角,共有几个呢
1.三角形的外角的概念
A
B
C
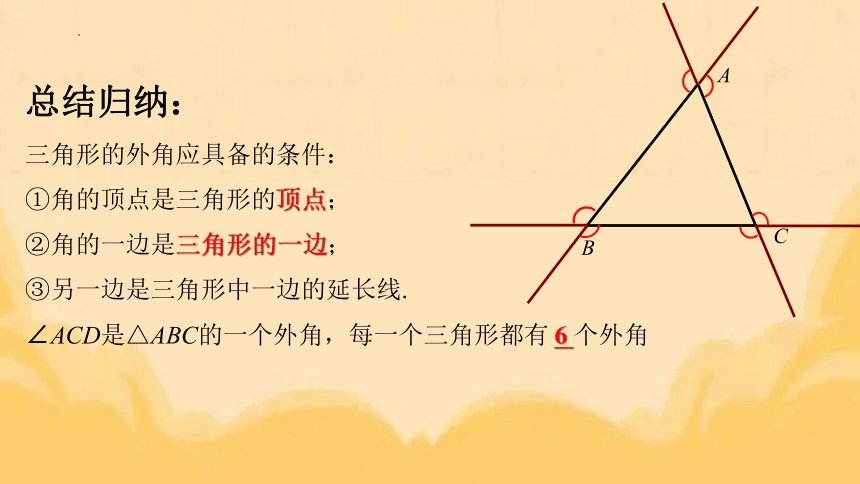
总结归纳:
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角,每一个三角形都有 6 个外角
A
B
C
问题2:在△ABC中,∠A=60°,∠B=50°,则∠ACD=_____;
如图,任意一个△ABC的外角∠ACD与∠A,∠B有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠ACD+∠ACB=180°
∴∠A+∠B=∠ACD.
合作探究---三角形的外角的性质
三角形内角和定理的推论
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
数学语言:
∵ ∠ACD是△ABC的一个外角
∴ ∠ACD= ∠A+ ∠B.
例2. 如图,是△ABC的一个外角,若∠A=44°,∠C=56°,
则∠CBD=_________
变式训练2. 求出下列图形中x的值.
例3:如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求:
(1)∠B 的度数;(2)∠C的度数.
变式训练3:如图,在△ABC中,AE平分∠BAC,
若∠B=70°,∠C=30°,求∠DEA的度数
定义 三角形的一边与另一边的延长线组成的角,叫做三角形的______.如________为△ABC的一个外角. 基本图形
性质 三角形的外角等于与它不相邻的两个内角的和.如__________=_____+________.
课堂小结
外角
∠ACD
∠ACD
∠A
∠B
课堂检测
1.判断下列命题的对错.
(1)三角形的外角和是指三角形的所有外角的和. ( )
(2)三角形的一个外角等于两个内角的和. ( )
(3)三角形的一个外角大于任何一个内角. ( )
2.如图,在△ABC中,点D在AB的延长线上.
(1)若∠A=60°,∠C=50°,则∠CBD=______°;
(2)若∠C=40°,∠CBD=105°,则∠A=_____°.
3.如图,在△ABC中,点D在BA的延长线上,∠B=40°,∠C=30°,则∠CAD的度数为 ( )
A. 110° B. 80° C. 70° D. 60°
4 .如图,AB∥CD,∠A=40°,∠D=45°,求∠1和∠2的度数.
C
拓展提升
5.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
求证:∠BAC=∠B+2∠E.
课后作业
1.书本P16 1(写书本上)
2.书本P17 8,9(作业本)
3.拓展选做
§11.2.2 三角形的外角
回顾旧知
1.三角形内角和等于_______________.
180 °
2.如图,在△ABC中, ∠A=70°, ∠B=60°,
则∠ACB= .
50 °
阅读书本P14-15 3分钟
合作探究---三角形的外角的概念
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACD是△ABC的一个外角
C
B
A
D
例1:判断下列图中的∠1是否为△ABC的外角.
问题1:如图,试着画出△ABC的所有外角,共有几个呢
1.三角形的外角的概念
A
B
C
总结归纳:
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角,每一个三角形都有 6 个外角
A
B
C
问题2:在△ABC中,∠A=60°,∠B=50°,则∠ACD=_____;
如图,任意一个△ABC的外角∠ACD与∠A,∠B有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠ACD+∠ACB=180°
∴∠A+∠B=∠ACD.
合作探究---三角形的外角的性质
三角形内角和定理的推论
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
数学语言:
∵ ∠ACD是△ABC的一个外角
∴ ∠ACD= ∠A+ ∠B.
例2. 如图,是△ABC的一个外角,若∠A=44°,∠C=56°,
则∠CBD=_________
变式训练2. 求出下列图形中x的值.
例3:如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求:
(1)∠B 的度数;(2)∠C的度数.
变式训练3:如图,在△ABC中,AE平分∠BAC,
若∠B=70°,∠C=30°,求∠DEA的度数
定义 三角形的一边与另一边的延长线组成的角,叫做三角形的______.如________为△ABC的一个外角. 基本图形
性质 三角形的外角等于与它不相邻的两个内角的和.如__________=_____+________.
课堂小结
外角
∠ACD
∠ACD
∠A
∠B
课堂检测
1.判断下列命题的对错.
(1)三角形的外角和是指三角形的所有外角的和. ( )
(2)三角形的一个外角等于两个内角的和. ( )
(3)三角形的一个外角大于任何一个内角. ( )
2.如图,在△ABC中,点D在AB的延长线上.
(1)若∠A=60°,∠C=50°,则∠CBD=______°;
(2)若∠C=40°,∠CBD=105°,则∠A=_____°.
3.如图,在△ABC中,点D在BA的延长线上,∠B=40°,∠C=30°,则∠CAD的度数为 ( )
A. 110° B. 80° C. 70° D. 60°
4 .如图,AB∥CD,∠A=40°,∠D=45°,求∠1和∠2的度数.
C
拓展提升
5.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
求证:∠BAC=∠B+2∠E.
课后作业
1.书本P16 1(写书本上)
2.书本P17 8,9(作业本)
3.拓展选做
