用代入法解二元一次方程组(福建省厦门市集美区)
文档属性
| 名称 | 用代入法解二元一次方程组(福建省厦门市集美区) |  | |
| 格式 | rar | ||
| 文件大小 | 116.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-02 18:16:00 | ||
图片预览






文档简介
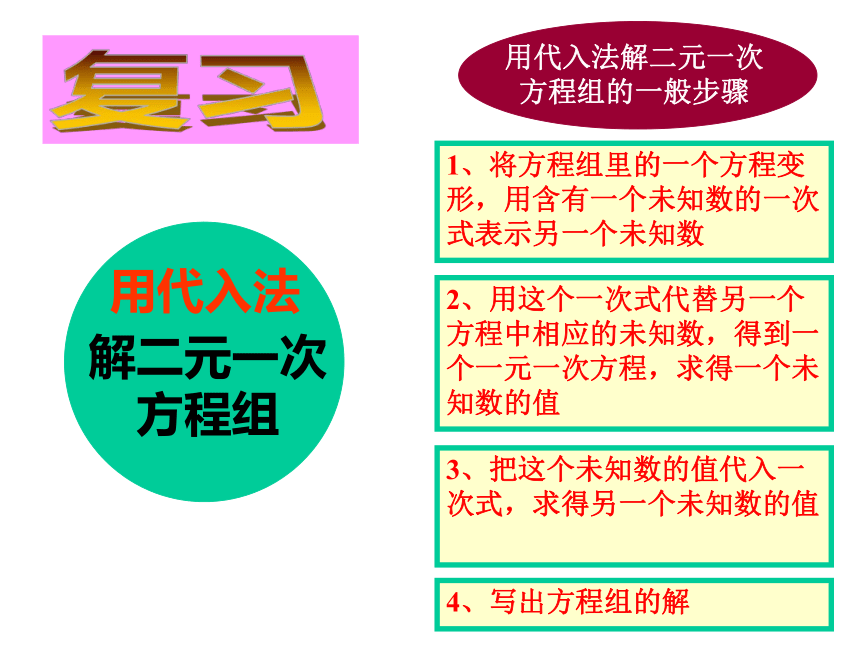
课件14张PPT。 初一(6)班复习1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值3、把这个未知数的值代入一次式,求得另一个未知数的值4、写出方程组的解1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值3、把这个未知数的值代入一次式,求得另一个未知数的值4、写出方程组的解练 习 题1、 解方程组讨论解:①②由①得:s = 3/2 t③把③代入②得:3×3/2 t – 2t = 59/2 t – 2t = 59t – 4t = 105t = 10t = 2把t = 2代入③,得s = 3/2 t= 3/2×2= 3∴s = 3t = 2解:①②由①得:x = ③把③代入②得:3(8 +7y)-16y –20 = 024+21y – 16y –20 = 0y = -4/5把y = -4/5代入③,得∴x = 6/5y = -4/52x =8 + 7yx = =6/5例1 解方程组解:①②由①得:s = 3/2 t③把③代入②得:3×3/2 t – 2t = 59/2 t – 2t = 59t – 4t = 105t = 10t = 2把t = 2代入③,得s = 3/2 t= 3/2×2= 3∴s = 3t = 2练 习 题1、 用代入法解下列方程组:解:原方程组可化为:①②由①得:x = 2 – 3y③把③代入②得:-2(2 – 3y)+ 6y = 1-4 + 6y + 6y = 16y + 6y = 1 + 412y = 5y = 5/12把y = 5/12 代入③,得x = 2 – 3y= 2 - 3×5/12x = 3/4∴x = 3/4y = 5/12解:原方程组可化为:3x – 2y = 6x – y = 2①②由②得:把③代入①得:x = 2 + y③3(2 + y)- 2y = 66 + 3y – 2y = 6y = 0把y = 0 代入③,得:x = 2 + y= 2 + 0x = 2∴x = 2y = 0解方程组:练 习 题1、若方程5x 2m+n+4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.解:根据已知条件得:2m + n = 13m – 2n = 1①②由①得:把③代入②得:n = 1 –2m③3m – 2(1 – 2m)= 13m – 2 + 4m = 17m = 3m = 3/7把m = 3/7 代入③,得:n = 1 –2m思 考 题-2 + 2a = 3b-a – 2b = 1①②思 考 题由②得:a = -2b - 1③把③代入①得:-2 + 2(-2b – 1)= 3b-2 – 4b – 2 = 3b-4b – 3b = + 2 + 2-7b = 4b = -4/7把b = -4/7 代入③,得:a = 1/7∴a = 1/7b = -4/7a = -2b - 1= -2×(-4/7)-1思 考 题解:①②由①得:y = 2x - 3③把③代入②得:3x + 2(2x – 3)= 83x + 4x – 6 = 83x + 4x = 8 + 67x = 14x = 2把x = 2 代入③,得:y = 2x - 3= 2×2 - 3=1④⑤解得:a = 1b = -1思 考 题4、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.解:根据已知条件,得:①②由①得:y = 2 – 3x把③代入②得:③5x + 2(2 – 3x)- 2 = 05x + 4 – 6x – 2 = 05x – 6x = 2 - 4-x = -2x = 2把x = 2 代入③,得:y = 2 – 3x= 2 - 3×2= -4答:x 的值是2,y 的值是-4.思 考 练 习 题1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值3、把这个未知数的值代入一次式,求得另一个未知数的值4、写出方程组的解
