湘教版数学九年级上册2.1一元二次方程 说课课件(共22张PPT)
文档属性
| 名称 | 湘教版数学九年级上册2.1一元二次方程 说课课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
湘教版九年级上册第二章第一节
一元二次方程
一、背景分析
二、教学目标设计
三、教法学法分析
四、教学媒体设计
五、教学过程设计
六、评价分析
说课提纲
一、背景分析
1、学习任务分析
《一元二次方程》这节课是本章内容的的第一课时,这节课主要是从具体问题中抽象出一元二次方程,并给出了一元二次方程的定义和一般形式,是一堂概念课,是本章内容的基础.
学生已经学习过一元一次方程的建模,掌握了一元一次方程的定义,一般形式及应用,在知识上和方法上都有一定的基础.但是学生的抽象思维能力还不是很强,灵活运用知识解决问题的能力也有待提高.
2、 学生情况分析
教学重点:
①使学生感受到一元二次方程来源于生活,并能从具体问题中抽象出一元二次方程;
②能判断一元二次方程并将一元二次方程化成一般形式
教学难点:
①从具体问题中抽象出一元二次方程;
②理解并会用一元二次方程的一般形式中a≠0这一条件。
3、 重点.难点的定位
二、教学目标设计
根据新课标的目标要求和对教材的分析,结合学生已有的知识基础和能力,我确定了如下目标:
【知识与技能目标】
(1)理解一元二次方程的意义
(2)能熟练地把一元二次方程整理成一般形式并能指出它的二次项
系数、一次项系数及常数项
【过程与方法目标】
通过分析实际问题的数量关系,把实际问题转化为数学模型(一元二次方程)的过程,使学生感受方程是刻画现实世界数量关系的工具,增加对一元二次方程的感性认识
【情感、态度、价值观目标】
通过探索建立一元二次方程模型的过程,使学生积极参与数学学习活动,增进对方程的认识,提高学生分析问题、解决问题的能力
三、教法·学法分析
1、教法
基于本节课内容的特点和初三学生的基础,我以 “启发式”教学法为主进行教学。教师作引导,学生为主体,以学生的互动学习为主,提高学生的观察、分析、概括能力, 在合作、交流的气氛下进行师生互动,培养学生的自学能力和创新意识。
根据学生的思维特点、认知水平,遵循“学习有用的数学”的教育理念,让每一个学生自主参与课堂的知识构建。引导学生综合归纳,以自主探索为主,学会合作交流,在师生互动、生生互动中让每个学生动口,动手,动脑,培养学生学习的主动性和积极性,使学生由“想学”到“会学”变“学会”和“善学”。
2、学法
采用多媒体辅助教学,由实际问题建立一元二次方程的模型;将判断题以游戏抢答的形式出现,充分的调动学生的积极性,激发学生的学习热情;
3、教学手段
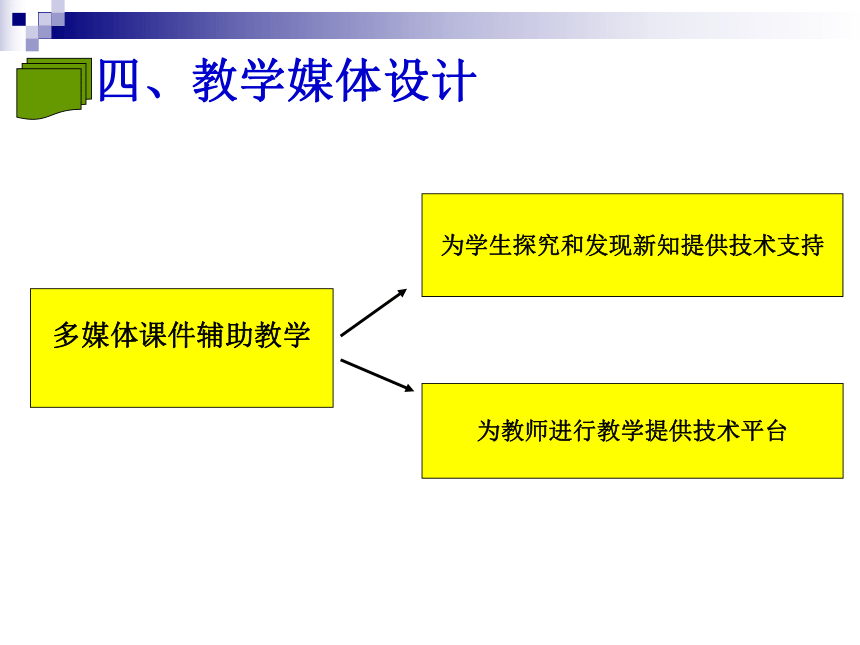
四、教学媒体设计
为教师进行教学提供技术平台
为学生探究和发现新知提供技术支持
多媒体课件辅助教学
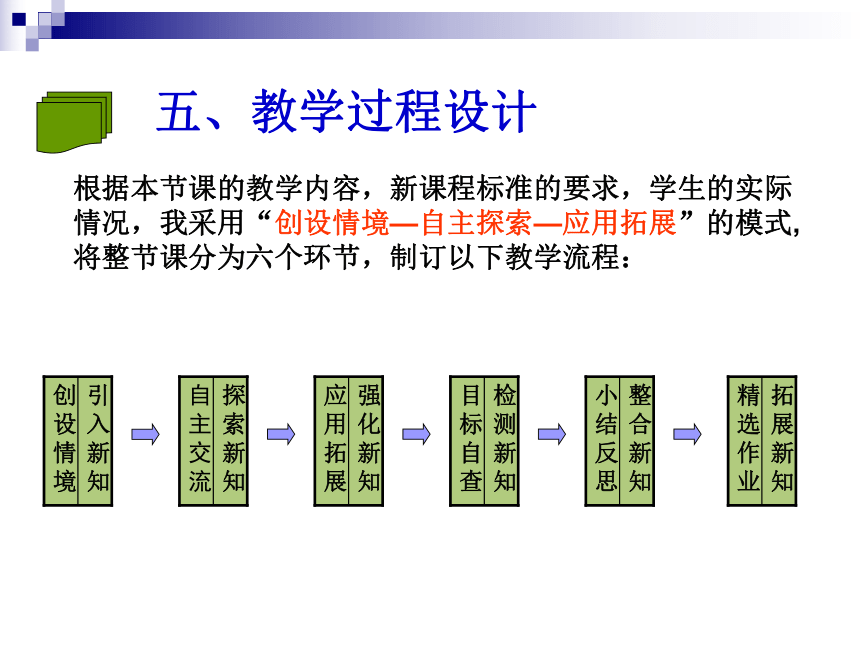
根据本节课的教学内容,新课程标准的要求,学生的实际情况,我采用“创设情境—自主探索—应用拓展”的模式,将整节课分为六个环节,制订以下教学流程:
五、教学过程设计
引入新知
创设情境
探索新知
自主交流
整合新知
小结反思
检测新知
目标自查
强化新知
应用拓展
拓展新知
精选作业
创设情境,导入新知
过程1
问题一:
下图是某校教学楼和厕所的平面图,根据“两点之间线段最短”小花选择了走对角线,这里本没有路,被她踩出了路,这种做法对吗?已知矩形草地的长比宽多12米,面积为540平方米,怎样求矩形的长和宽 你能帮她算算这样能少走几米路?
设计意图:
问题的提出激发了学生的求知欲望,让学生感到数学来源于生活,于是 “我想学”,调动他们学习本章内容的积极性;另一方面抓住契机,结合我市当前的“五创”,教育学生做一个文明市民.
创建文明城市,人人有责
分析:设宽为x米,则长为(x+12)米,则可以
列出方程: x (x+12)=540
整理为: x2+12x-540=0 ①
厕所
x
教学楼
X+12
设计意图:教学生如何分析问题,使学生“会学”,培养学生处理信息的能力和抽象思维能力。
分析:设经过ts小明与小亮相遇,则在这段时间内,小明骑车行驶的路程为
3t,小亮行驶的路程为
,
可列方程3t =
整理得:0.005t2- t =0 ②
问题2:小明和小亮分别从家里出发骑车去学校,在离学校还有1km处第一次相遇,此时他们的骑车速度为3m/s和2m/s。小明继续以3m/s的速度匀速前进;而小亮则逐渐加快速度,以0.01m/s2的加速度匀加速前进,已知匀加速运动求路程s的公式是:
其中t是时间,v0是初速度的大小,a是加速度的大小。你能计算出经过多长的时间他们再次相遇吗?
过程2
自主交流,探索新知
设计意图:培养学生的观察和综合归纳的能力.
问:他们有什么共同点?
①它们分别含有几个未知数?
②它们的左边分别是 x 和 t 的几次多项式?
一元二次方程的定义和一般形式:ax2+bx+c=0
(a,b,c是已知数,其中a≠0)
x2+12x-540=0
观察方程
① 和
回到方程①和②分别指出它们的二次项系数,一次项系数和常数项 。
0.005 t2-t=0 ②
为了让学生进一步掌握一元二次方程的定义和一般形式,我按由易到难,由能力训练到思维方法训练的顺序,分别以不同的形式精心安排了三组练习。
应用拓展,强化新知
过程3
游戏规则:举手最快的同学用锤子敲开你选中的“鸡蛋”,并判断里
面的式子是否为一元二次方程。答对加十分,答错扣十
分,得分最多的组为优胜组。
游戏:
1
3x2+2x+1
2
3x2-2y=3
3
3x+5=2x-1
4
(x+1)2=x2-4
5
6
7
x2+5x=6
8
3(x-4)=x2-12
9
3x(x-1)=5(x+2)
10
(x+2)(x-2)=0
11
ax2+bx+c=0
12
设计意图:将判断题以游戏的形式出现能够调动学生的积极性, 扩大课堂容量。让同学们“互评互学”
例题1 请将游戏中得到的一元二次方程写成一般形式并求出它们的
二次项系数,一次项系数以及常数项,完成表格。
设计意图:突出重点,让每个同学都“学会”求一元二次方程的一般形式并能找出它们的二次项系数,一次项系数以及常数项。
方程 一般形式 二次项系数a 一次项系数b 常数项c
x2+5x=6
(x+2)(x-2)=0
3(x-4)=x2-12
3x(x-1)=5(x+2)
例2:
关于x的方程
问:⑴a为何值时,它是一元二次方程?
⑵a为何值时,它是一元一次方程?
设计意图:突破难点,训练学生的“分类讨论”的数学思想,使学生掌握学习方法,成为“善学”的能手
(教材第20页B组第6题)
目标自查,检测新知
过程4
1、已知x=1是关于x的一元二次方程2 x2+kx-1=0的一个根,则实数k=_____
2、一元二次方程(x+1)2-x=3(x2-2)化为一般形式是___________,其中二次项系数为_____,一次项系数为_____,常数项为______.
4、在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,使整个挂图总面积为5400cm2,设金色纸边宽为xcm,则用x的代数式表示挂画的长为________cm,宽为_______cm,面积为_________cm2, 可列方程______________,化为一般形式是___________
|x|
|x|
|x|
|x|
80cm
50cm
5、如图,长5m的梯子斜靠在墙上,梯子的底端与墙的距离是3m,如果梯子底端向右滑动的距离与梯子顶端向下滑动的距离相等,求梯子滑动 的距离x所满足的方程__________化为一般形式是_____________
3、若关于X的一元二次方程(m-2)x2+3x+m2-4=0的
常数项为0,则m=_____
小结反思,整合新知
过程5
说一说:这节课我学到了……
体验了……
困难是……
1.课本 P4 A组 T1 T3
P5 B组 T1 T2
精选作业,拓展新知
过程6
2.如图所示,某住宅小区内有一栋建筑,占地为一边长为35m的正方形,现打算拆除建筑并在其正中间铺上一面积为900m2的正方形草坪,使四周留出的人行道的宽度相等,请问你能求出人行道的宽度吗?
(35-2X)2=900
设计意图:承上启下
900m2
30m
板书设计
一元二次方程
1、定义:
2、一般形式:
例题1
例题2
x2+12x-540=0 ①
0.005 t2-t=0 ②
方程 一般形式 二次项系数a 一次项系数b 常数项c
x2+5x=6
(x+2)(x-2)=0
3(x-4)=x2-12
3x(x-1)=5(x+2)
六、评价分析:
评价的目的是全面考查学生的学习状况,激励学生的学习热情,促进学生的全面发展,在教学中我采用师评、互评、自评相结合的方式,设置了三个评价点。
1、情境引入中的评价:以师评为主,关注学生参与活动的情绪和状态,对有独特想法或结论的学生,给予鼓励,对学有困难的学生推迟评价,让学生在学习过程中获得成功的喜悦。
2、解决问题中的评价:以互评为主,关注学生思维发展的水平和解决问题的能力。
3、小结反思中的评价:以自评为主,关注学生知识与技能上的发展及数学活动经验的积累程度。
湘教版九年级上册第二章第一节
一元二次方程
一、背景分析
二、教学目标设计
三、教法学法分析
四、教学媒体设计
五、教学过程设计
六、评价分析
说课提纲
一、背景分析
1、学习任务分析
《一元二次方程》这节课是本章内容的的第一课时,这节课主要是从具体问题中抽象出一元二次方程,并给出了一元二次方程的定义和一般形式,是一堂概念课,是本章内容的基础.
学生已经学习过一元一次方程的建模,掌握了一元一次方程的定义,一般形式及应用,在知识上和方法上都有一定的基础.但是学生的抽象思维能力还不是很强,灵活运用知识解决问题的能力也有待提高.
2、 学生情况分析
教学重点:
①使学生感受到一元二次方程来源于生活,并能从具体问题中抽象出一元二次方程;
②能判断一元二次方程并将一元二次方程化成一般形式
教学难点:
①从具体问题中抽象出一元二次方程;
②理解并会用一元二次方程的一般形式中a≠0这一条件。
3、 重点.难点的定位
二、教学目标设计
根据新课标的目标要求和对教材的分析,结合学生已有的知识基础和能力,我确定了如下目标:
【知识与技能目标】
(1)理解一元二次方程的意义
(2)能熟练地把一元二次方程整理成一般形式并能指出它的二次项
系数、一次项系数及常数项
【过程与方法目标】
通过分析实际问题的数量关系,把实际问题转化为数学模型(一元二次方程)的过程,使学生感受方程是刻画现实世界数量关系的工具,增加对一元二次方程的感性认识
【情感、态度、价值观目标】
通过探索建立一元二次方程模型的过程,使学生积极参与数学学习活动,增进对方程的认识,提高学生分析问题、解决问题的能力
三、教法·学法分析
1、教法
基于本节课内容的特点和初三学生的基础,我以 “启发式”教学法为主进行教学。教师作引导,学生为主体,以学生的互动学习为主,提高学生的观察、分析、概括能力, 在合作、交流的气氛下进行师生互动,培养学生的自学能力和创新意识。
根据学生的思维特点、认知水平,遵循“学习有用的数学”的教育理念,让每一个学生自主参与课堂的知识构建。引导学生综合归纳,以自主探索为主,学会合作交流,在师生互动、生生互动中让每个学生动口,动手,动脑,培养学生学习的主动性和积极性,使学生由“想学”到“会学”变“学会”和“善学”。
2、学法
采用多媒体辅助教学,由实际问题建立一元二次方程的模型;将判断题以游戏抢答的形式出现,充分的调动学生的积极性,激发学生的学习热情;
3、教学手段
四、教学媒体设计
为教师进行教学提供技术平台
为学生探究和发现新知提供技术支持
多媒体课件辅助教学
根据本节课的教学内容,新课程标准的要求,学生的实际情况,我采用“创设情境—自主探索—应用拓展”的模式,将整节课分为六个环节,制订以下教学流程:
五、教学过程设计
引入新知
创设情境
探索新知
自主交流
整合新知
小结反思
检测新知
目标自查
强化新知
应用拓展
拓展新知
精选作业
创设情境,导入新知
过程1
问题一:
下图是某校教学楼和厕所的平面图,根据“两点之间线段最短”小花选择了走对角线,这里本没有路,被她踩出了路,这种做法对吗?已知矩形草地的长比宽多12米,面积为540平方米,怎样求矩形的长和宽 你能帮她算算这样能少走几米路?
设计意图:
问题的提出激发了学生的求知欲望,让学生感到数学来源于生活,于是 “我想学”,调动他们学习本章内容的积极性;另一方面抓住契机,结合我市当前的“五创”,教育学生做一个文明市民.
创建文明城市,人人有责
分析:设宽为x米,则长为(x+12)米,则可以
列出方程: x (x+12)=540
整理为: x2+12x-540=0 ①
厕所
x
教学楼
X+12
设计意图:教学生如何分析问题,使学生“会学”,培养学生处理信息的能力和抽象思维能力。
分析:设经过ts小明与小亮相遇,则在这段时间内,小明骑车行驶的路程为
3t,小亮行驶的路程为
,
可列方程3t =
整理得:0.005t2- t =0 ②
问题2:小明和小亮分别从家里出发骑车去学校,在离学校还有1km处第一次相遇,此时他们的骑车速度为3m/s和2m/s。小明继续以3m/s的速度匀速前进;而小亮则逐渐加快速度,以0.01m/s2的加速度匀加速前进,已知匀加速运动求路程s的公式是:
其中t是时间,v0是初速度的大小,a是加速度的大小。你能计算出经过多长的时间他们再次相遇吗?
过程2
自主交流,探索新知
设计意图:培养学生的观察和综合归纳的能力.
问:他们有什么共同点?
①它们分别含有几个未知数?
②它们的左边分别是 x 和 t 的几次多项式?
一元二次方程的定义和一般形式:ax2+bx+c=0
(a,b,c是已知数,其中a≠0)
x2+12x-540=0
观察方程
① 和
回到方程①和②分别指出它们的二次项系数,一次项系数和常数项 。
0.005 t2-t=0 ②
为了让学生进一步掌握一元二次方程的定义和一般形式,我按由易到难,由能力训练到思维方法训练的顺序,分别以不同的形式精心安排了三组练习。
应用拓展,强化新知
过程3
游戏规则:举手最快的同学用锤子敲开你选中的“鸡蛋”,并判断里
面的式子是否为一元二次方程。答对加十分,答错扣十
分,得分最多的组为优胜组。
游戏:
1
3x2+2x+1
2
3x2-2y=3
3
3x+5=2x-1
4
(x+1)2=x2-4
5
6
7
x2+5x=6
8
3(x-4)=x2-12
9
3x(x-1)=5(x+2)
10
(x+2)(x-2)=0
11
ax2+bx+c=0
12
设计意图:将判断题以游戏的形式出现能够调动学生的积极性, 扩大课堂容量。让同学们“互评互学”
例题1 请将游戏中得到的一元二次方程写成一般形式并求出它们的
二次项系数,一次项系数以及常数项,完成表格。
设计意图:突出重点,让每个同学都“学会”求一元二次方程的一般形式并能找出它们的二次项系数,一次项系数以及常数项。
方程 一般形式 二次项系数a 一次项系数b 常数项c
x2+5x=6
(x+2)(x-2)=0
3(x-4)=x2-12
3x(x-1)=5(x+2)
例2:
关于x的方程
问:⑴a为何值时,它是一元二次方程?
⑵a为何值时,它是一元一次方程?
设计意图:突破难点,训练学生的“分类讨论”的数学思想,使学生掌握学习方法,成为“善学”的能手
(教材第20页B组第6题)
目标自查,检测新知
过程4
1、已知x=1是关于x的一元二次方程2 x2+kx-1=0的一个根,则实数k=_____
2、一元二次方程(x+1)2-x=3(x2-2)化为一般形式是___________,其中二次项系数为_____,一次项系数为_____,常数项为______.
4、在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,使整个挂图总面积为5400cm2,设金色纸边宽为xcm,则用x的代数式表示挂画的长为________cm,宽为_______cm,面积为_________cm2, 可列方程______________,化为一般形式是___________
|x|
|x|
|x|
|x|
80cm
50cm
5、如图,长5m的梯子斜靠在墙上,梯子的底端与墙的距离是3m,如果梯子底端向右滑动的距离与梯子顶端向下滑动的距离相等,求梯子滑动 的距离x所满足的方程__________化为一般形式是_____________
3、若关于X的一元二次方程(m-2)x2+3x+m2-4=0的
常数项为0,则m=_____
小结反思,整合新知
过程5
说一说:这节课我学到了……
体验了……
困难是……
1.课本 P4 A组 T1 T3
P5 B组 T1 T2
精选作业,拓展新知
过程6
2.如图所示,某住宅小区内有一栋建筑,占地为一边长为35m的正方形,现打算拆除建筑并在其正中间铺上一面积为900m2的正方形草坪,使四周留出的人行道的宽度相等,请问你能求出人行道的宽度吗?
(35-2X)2=900
设计意图:承上启下
900m2
30m
板书设计
一元二次方程
1、定义:
2、一般形式:
例题1
例题2
x2+12x-540=0 ①
0.005 t2-t=0 ②
方程 一般形式 二次项系数a 一次项系数b 常数项c
x2+5x=6
(x+2)(x-2)=0
3(x-4)=x2-12
3x(x-1)=5(x+2)
六、评价分析:
评价的目的是全面考查学生的学习状况,激励学生的学习热情,促进学生的全面发展,在教学中我采用师评、互评、自评相结合的方式,设置了三个评价点。
1、情境引入中的评价:以师评为主,关注学生参与活动的情绪和状态,对有独特想法或结论的学生,给予鼓励,对学有困难的学生推迟评价,让学生在学习过程中获得成功的喜悦。
2、解决问题中的评价:以互评为主,关注学生思维发展的水平和解决问题的能力。
3、小结反思中的评价:以自评为主,关注学生知识与技能上的发展及数学活动经验的积累程度。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
